Современные достижения в области вычислительной техники дают возможность решать ресурсоемкие задачи в различных областях науки при построении моделей и обработке больших массивов данных прежде всего благодаря организации распределенных вычислений с помощью суперкомпьютеров и вычислительных кластеров. В последнее время к ним присоединились и мобильные устройства по причине нарастающей мощности и увеличения времени работы.
При решении ряда трудоемких задач портативные устройства используются не как инструмент для проведения научных вычислений, а скорее как средство взаимодействия с облаком через межплатформенное ПО [1–5]. С другой стороны, для менее затратных в смысле вычислительных ресурсов задач, в том числе при их разбиении [6], становится возможным непосредственное использование мобильного устройства [7–11]. Показателем целесообразности проведения научных вычислений на мобильных платформах является тот факт, что портативные устройства были включены в проекты для организации быстрых распределенных вычислений BOINC [2, 12] и Folding@home [13]. Тем не менее, даже при оптимальном распределении задач [6] разработка мобильных приложений требует учета ограничений на использование вычислительных ресурсов, таких как время отклика, размер используемой памяти и потребляемая мощность [7–11, 14]. Следовательно, алгоритмы, реализуемые на устройстве, должны быть адаптированы согласно предъявляемым требованиям [11, 15, 16]. Таким образом, целью данной работы является адаптация алгоритма оценки коэффициентов Фурье в базисе, необходимых для построения аналитических моделей и проведения научных вычислений, в том числе при обработке больших массивов данных [9, 11].
Методы и алгоритмы
Введем ряд понятий, необходимых для математической постановки задачи. Обозначим Lk(t, g) ортогональную функцию Лагерра k-го порядка, для которой справедливо следующее рекуррентное соотношение: kLk(t, g)=(2k–1–t)Lk–1(t, g)– –(k–1)Lk–2(t, g) в Гильбертовом пространстве tÎR+ с параметром масштаба gÎГ, где ГÎ{gÎГ: g>0}, и с единичной весовой функцией.
Принимая во внимание  представим оценку функции
представим оценку функции  в виде конечного ряда:
в виде конечного ряда: 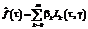 , где коэффициенты Фурье могут быть определены как
, где коэффициенты Фурье могут быть определены как
 , (1)
, (1)
и  является нормой базисных функций.
является нормой базисных функций.
Тогда представим коэффициенты Фурье (1) с помощью численно-аналитической квадратуры, позволяющей получить оценку с заранее заданной точностью [17]:
 (2)
(2)
где ai, bi являются коэффициентами линейной интерполяции в соответствии с
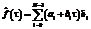 , (3)
, (3)
 – индикатор состояния.
– индикатор состояния.
Вычислить квадратуру (2) с заданной погрешностью [17] можно при аналитическом определении интегралов  и
и 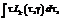 которые могут быть представлены рекуррентно:
которые могут быть представлены рекуррентно:
 (4)
(4)
 (5)
(5)
Данные соотношения можно классифицировать как рекурсии второго порядка с экспоненциальным временем затрат. Как общее правило для решения рекурсий можно сохранять все значения в массив вместо выполнения рекурсивной программы, что, в свою очередь, приведет к существенному увеличению требуемой памяти. Таким образом, требуется разработать алгоритм для исключения упомянутых недостатков, а именно, снизить временные затраты и размер требуемой памяти, которые формируют описанные выше требования к разработке мобильного приложения.
Для решения поставленной задачи воспользуемся аппаратом определения коэффициентов связи между базисными функциями, описанным в работах [18–20].
Представим  как
как
 , (6)
, (6)
где 
 (7)
(7)
где 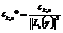 .
.
Подставляя (7) в (6), получим
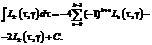 (8)
(8)
При проведении вычислительных экспериментов опустим рассмотрение (5), так как данное соотношение не предполагает рекурсивных вызовов, а для оценки коэффициентов по формуле (2) при программной реализации алгоритм нахождения  будет зависеть от соответствующего алгоритма
будет зависеть от соответствующего алгоритма
Вычислительные эксперименты
В рамках данного исследования была проведена серия вычислительных экспериментов с целью проверки адекватности представленных алгоритмов и их соответствия требованиям, предъявляемым к разработке ПО для мобильного устройства.
В таблице представлены результаты, полученные с помощью MATLAB Profiler при значениях k = {5, 10, 15, 20}, g = 1, N = 10 000, Dt = 0,001. Заметим, что N и Dt требуются для формирования матрицы значений при заданном аргументе tзад=10. Параметры, анализируемые при проведении экспериментов, – количество вызовов функции, затраты времени (CPU), размер выделяемой памяти. Эксперименты проводились на ЭВМ с характеристиками: 4GB DDR3, Intel Core i3 CPU 2.53 GHz, ОС Windows 7 (x64).
Для компактного формирования таблицы введем следующие обозначения: Lrec – функция, реализующая алгоритм вычисления Lk(t, g) рекуррентно; intLrec – функция, реализующая алгоритм вычисления  рекуррентно; Lcon, intLcon – соответствующие функции для вычисления указанных характеристик с помощью коэффициентов связи и с сохранением значений.
рекуррентно; Lcon, intLcon – соответствующие функции для вычисления указанных характеристик с помощью коэффициентов связи и с сохранением значений.
Как видно из таблицы, алгоритмы с реализацией связанных коэффициентов позволяют существенно снизить затрачиваемые временные ресурсы за счет исключения рекурсии, однако повышают затраты памяти, но незначительно.

При использовании интерполяционных формул (3) более высокого порядка необходимо создать алгоритм для вычисления коэффициентов связи для общего случая 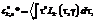
 , nÎN, что является дальнейшим направлением данных исследований.
, nÎN, что является дальнейшим направлением данных исследований.
Таким образом, при создании и тестировании программной реализации на базе разработанных алгоритмов проводился анализ временных затрат как более критичного показателя на реальном мобильном устройстве при изменении параметров m и N.
Программная реализация
Созданные и проанализированные алгоритмы для вычисления функций Lrec, intLrec, Lcon, intLcon были представлены как фрагменты кода на языке Java для реализации на мобильном устройстве Nexus 7 с характеристиками: Nvidia Tegra 3, 1GB DDR, четырехъядерный CPU 1200 MHz, ОС Android v. 4.4.1.
|
# рекуррентные соотношения
public static double recurrentFunctionLaggera (double point, double gamma, int k) {
if (k == 0) {
return Math.exp(-gamma * point / 2);
}
if (k == 1) {
return Math.exp(-gamma * point / 2) * (1 - gamma * point);
}
return (2 * k - 1 - gamma * point) * recurrentFunctionLaggera (point, gamma, k - 1) / k - (k - 1) * recurrentFunctionLaggera (point, gamma, k - 2) / k;
}
public static double recurrentIntegral1 (double point, double gamma, int k) {
if (m == 0) {
return -2 * Math.exp(-gamma * point / 2) / gamma;
}
double tmp = 0;
tmp += -2 * recurrentFunctionLaggeraPoint(point, gamma, k) / gamma;
for (int i = m - 1; i >= 0; i--) {
tmp += -2 * recurrentIntegral1(point, gamma, i);
}
return tmp
}
|
|
# соотношения с коэффициентами связи
public static double basicIntegral1(double point, double gamma, int k) {
double[] functionLaggera = basicFunctionLaggera(point, gamma, k);
double result = 0;
for (int v = 0; v < functionLaggera.length; v++) {
result += Math.pow(-1, k + v) * functionLaggera[v];
}
result *= -4 / gamma;
result -= -2 * functionLaggera[functionLaggera.length - 1] / gamma;
return result;
}
public static double[] basicFunctionLaggera(double point, double gamma, int k) {
double[] result = new double[k + 1];
result[0] = Math.exp(-gamma * point / 2);
if (k == 0) {
return result;
}
result[1] = Math.exp(-gamma * point / 2) * (1 - gamma * point);
for (int i = 2; i < result.length; i++) {
result[i] = (2 * i - 1 - gamma * point) * result[i - 1] / i - (i - 1) * result[i - 2] / i;
}
return result;
}
|
Разработанная программная реализация в рамках пространственной схемы взаимодействия объектов [21] выполняет следующие задачи [22]:
– загрузка исходного набора данных;
– расчет коэффициентов Фурье (2) согласно каждому из анализируемых алгоритмов (4) и (7);
– сохранение результатов работы программы в файл;
– построение графических зависимостей с анализом временных затрат.
Следует заметить, что анализ погрешности находится за рамками проводимых в данной работе исследований, направленных, в первую очередь, на улучшение вычислительных возможностей алгоритмов без потери точности. Таким образом, при проведении тестовых испытаний програм- мной реализации будем варьировать объем исходных данных и количество членов разложения ряда Фурье при одинаковых условиях, имея в виду некоторую заданную этими параметрами погрешность.
Для удобства восприятия полученных результатов на рисунках 1 и 2 представлены фрагменты зависимостей, полученных на основе результатов тестирования программы при обработке больших наборов данных. Следует отметить, что на каждом из рисунков график, расположенный ниже (б), является представлением зависимости временных затрат для соотношений с коэффициентами связи, которая слабо различима на графике, расположенном выше (а).

 Анализ приведенных зависимостей показывает, что использование квадратуры, включающей соотношения с коэффициентами связи, при оценке коэффициентов разложения позволяет значительно снизить временные затраты на вычисление коэффициентов разложения, и при увеличении объема данных и числа членов ряда Фурье получаемое преимущество возрастает.
Анализ приведенных зависимостей показывает, что использование квадратуры, включающей соотношения с коэффициентами связи, при оценке коэффициентов разложения позволяет значительно снизить временные затраты на вычисление коэффициентов разложения, и при увеличении объема данных и числа членов ряда Фурье получаемое преимущество возрастает.
Таким образом, в результате проведенных исследований были созданы эффективные алгоритмы для оценки коэффициентов разложения Фурье в базисе Лагерра, основанные на определении коэффициентов связи между базисными функциями для представления неопределенных интегралов, которые в последующем использовались при вычислении квадратуры. Как показали результаты вычислительных экспериментов, созданный алгоритм intLcon позволяет снизить временные затраты за счет исключения рекурсии при k = 10, N = 10 000 в 29 раз, при k = 20, N = 10 000 в 1895 раз, и в дальнейшем при увеличении порядка данное преимущество возрастает по сравнению с использованием intLrec. Для проведения исследований в условиях ограниченных ресурсов была создана программная реализация на мобильной платформе и проведены тестовые испытания, которые выявили преимущества intLcon по временным затратам при m = 10, N = 500 в 46 раз. Таким образом, с учетом требований, предъявляемых к разработке мобильных приложений, алгоритм, реализованный через расчет коэффициентов связи, и его программная реализация целесо- образны для анализа данных через оценку коэффициентов Фурье при ограниченных вычис- лительных ресурсах.
Литература
1. Fernando N., Loke S.W., Rahayu W. Mobile cloud computing: A survey. Future Generation Computer Systems, 2013, no. 1 (29), pp. 84–106.
2. Smaoui M., Garbey M. Improving volunteer computing scheduling for evolutionary algorithms. Future Generation Computer Systems, 2013, no. 1 (29), pp. 1–14.
3. Shiraz M., Sookhak M., Gani A., Shah S.A.A. A study on the critical analysis of computational offloading frameworks for mobile cloud computing. J. of Network and computer applications, 2015, vol. 47, pp. 47–60.
4. Liu J., Ahmed E., Shiraz M., Gani A., Buyya R., Qureshi A. Application partitioning algorithms in mobile cloud computing: Taxonomy, review and future directions. J. of Network and computer applications, 2015, vol. 48, pp. 99–117.
5. Калабин А.Л., Артемов И.Ю. Программный комплекс автоматизации процедуры сбора данных // Программные продукты и системы. 2013. № 2. С. 137–141.
6. Киселев Е.А., Аладышев О.С. Алгоритм эффективного размещения программ на ресурсах многопроцессорных вычислительных систем // Программные продукты и системы. 2012. № 4. С. 18–25.
7. Nirjon S., Dickerson R., Stankovic J., Shen G., Jiang X. sMFCC: Exploiting Sparseness in Speech for Fast Acoustic Feature Extraction on Mobile Devices – a Feasibility Study. Proc. 14th Workshop on Mobile Computing Systems and Applications, NY, ACM, 2013, no. 15; doi: 10.1145/2444776.2444787.
8. Rifa-Pous H., Herrera-Joancomarti J. Computational and Energy Costs of Cryptographic Algorithms on Handheld Devices. Future Internet, 2011, no. 3, pp. 31–48.
9. Kargupta H., Park B.-H. A Fourier spectrum-based approach to represent decision trees for mining data streams in mobile environments. Knowledge and Data Engineering, IEEE Transactions on, 2004, no. 2 (16), pp. 216–229.
10. Haddad A.W., Huange S., Boutin M., Delp E.J. Detection of symmetric shapes on a mobile devices with applications to automatic sign interpretation. Proc. of SPIE, 2012, vol. 8304; doi: 10.1117/12.908815.
11. Kulikovskikh I.M., Prokhorov S.A. Some lightweight algorithms for scientific computing in mobile technologies. Proc. 8th International Conference on Applied Mathematics and Scientific Computing, Sibenik, Croatia, 2013, pp. 40–41.
12. BOINC on Android (2012). URL: http://boinc.berkeley. edu/trac/wiki/AndroidBoinc (дата обращения: 18.02.2015).
13. New mobile app from Stanford and Sony lets your phone conduct research on breast cancer and Alzheimer's while it charges (2015). URL: http://news.stanford.edu/news/2015/january/sony-app-pande-011215.html (дата обращения: 18.02.2015).
14. Окунев Б.В. Энергосберегающий алгоритм работы мобильных устройств с беспроводными самоорганизующимися wi-fi-сетями (ad-hoc) // Программные продукты и системы. 2013. № 2. С. 198–201.
15. Захаров В., Мостяев А. Особенности переноса приложений на мобильные платформы // Программные системы и инструменты. 2014. № 15. C. 16–24.
16. Vasin Yu.G., Zherzdev S.V., Egorov A.A. Mobile Geoinformation system // Pattern Recognition and Image Analysis. 2009, no. 2 (19), pp. 342–348.
17. Прохоров С.А., Куликовских И.М. Численно-аналитический подход к вычислению интегралов при построении ортогональных моделей // Вестн. Сам. гос. техн. ун-та: Сер. Физ.-мат. науки. 2009. № 2 (19). С. 140–146.
18. Askey R. Orthogonal expansions with positive coefficients, Proc. Amer. Math. Soc., 1965, no. 16, pp. 1191–1194.
19. Ahmed H.M. Recurrence relations approach for expansion and connection coefficients in series of classical discrete orthogonal polynomials. Integral Transforms and Special Functions, 2009, no. 1 (20), pp. 23–34.
20. Doha E.H., Ahmed H.M. Efficient algorithms for construction of recurrence relations for the expansion and connection coefficients in series of quantum classical orthogonal polynomials. J. of Advanced Research, 2010, no. 1 (3), pp. 193–207.
21. Прохоров С.А., Куликовских И.М. Создание комплекса программ на основе пространственной схемы взаимодействия объектов // Программные продукты и системы. 2012. № 3. С. 5–8.
22. Куликовских И.М., Прохоров С.А., Целищев Д.В. Мобильное приложение для анализа коэффициентов разложения в условиях ограниченных вычислительных ресурсов. Свид. о гос. регистр. прогр. для ЭВМ от 08.09.14 г. Рег. № 2014619047.



 представим оценку функции
представим оценку функции  в виде конечного ряда:
в виде конечного ряда: 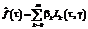 , где коэффициенты Фурье могут быть определены как
, где коэффициенты Фурье могут быть определены как , (1)
, (1) является нормой базисных функций.
является нормой базисных функций. (2)
(2)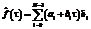 , (3)
, (3) – индикатор состояния.
– индикатор состояния. и
и 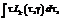 которые могут быть представлены рекуррентно:
которые могут быть представлены рекуррентно: (4)
(4) (5)
(5) , (6)
, (6)
 (7)
(7)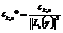 .
. 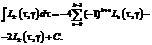 (8)
(8) будет зависеть от соответствующего алгоритма
будет зависеть от соответствующего алгоритма

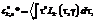
 , nÎN, что является дальнейшим направлением данных исследований.
, nÎN, что является дальнейшим направлением данных исследований.

