Современные информационные технологии на базе программно-математического обеспечения персональных компьютеров позволяют достаточно оперативно, используя численные методы, решать сложные, не поддающиеся аналитическому решению задачи из различных областей науки и техники, в частности, из области механики деформируемого твердого тела. В настоящее время для решения задач механики деформируемого твердого тела наибольшее распространение получили два метода: метод конечных разностей [1] и метод конечных элементов [2].
Метод конечных разностей – это численный метод решения дифференциальных уравнений, в основе которого лежит замена производных в дифференциальных уравнениях и соответствующих краевых условиях конечно-разностными операторами. В результате решение краевой задачи или задачи Коши сводится к решению системы конечно-разностных уравнений, а само решение представляется значениями искомых функций (перемещений или напряжений) в дискретном множестве узлов сетки, на которую разбивают область решения. Метод конечных элементов – это также численный метод решения дифференциальных и интегральных уравнений, в основе которого лежит разбиение области решения на конечные элементы произвольных размеров, но, как правило, одной формы. Искомая функция (например функция перемещений) внутри конечного элемента аппроксимируется, как правило, полиномом, коэффициенты которого выражаются через значения искомой функции в вершинах конечных элементов. В итоге решение задачи сводится к решению системы линейных алгебраических уравнений относительно значений искомой функции в узлах – вершинах совокупности конечных элементов, покрывающих расчетную область.
Для определения других искомых параметров решения в узлах сеточной области (например, напряжений или деформаций, если в качестве искомых функций использовались перемещения; либо деформаций и перемещений, если в качестве искомых функций использовались напряжения) вновь используются конечно-разностные операторы в методе конечных разностей или аппроксимирующие полиномы для каждого конечного элемента в методе конечных элементов. При этом значения параметров задачи в точках расчетной области вне узлов в методе конечных разностей остаются неопределенными.
Для решения задачи о вычислении искомых параметров в точках расчетной области вне узлов необходимо задаться характером распределения искомых параметров между узлами. Вот эта неопределенность является одним из недостатков метода конечных разностей. Обычно (и для упрощения построения решения) полагают, что искомые параметры между узлами изменяются по линейному закону. Но это предположение не всегда соответствует действительности. Кроме того, искомые параметры рассматриваемой задачи в механике деформируемого твердого тела, как правило, связаны друг с другом производным. Например, в [3] дифференциальное уравнение изогнутой оси стержня записывается относительно перемещений:
 . (1)
. (1)
Здесь V(z) – функция перемещений изогнутой оси стержня; q(z) – функция внешней распределенной нагрузки, действующей на стержень; EIx – изгибная жесткость стержня.
Следовательно, решая методом конечных разностей дифференциальное уравнение (1), мы определяем в каждом узле расчетной сеточной области функцию V(z). Вместе с тем угол поворота поперечного сечения стержня j(z) определяется по формуле
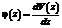 . (2)
. (2)
Изгибающий момент Mx(z) связан с перемещениями соотношением
 . (3)
. (3)
Для определения поперечной силы Qy(z) следует использовать зависимость
 . (4)
. (4)
Подобные зависимости, когда искомые параметры связаны друг с другом производными, имеют место во многих задачах механики деформируемого твердого тела, в частности, при изгибе тонких пластин [1].
Для вычисления прогиба, угла поворота, из- гибающего момента и поперечной силы в узлах расчетной сеточной области мы используем конечно-разностные операторы. Полагая, что между узлами функции прогибов, углов поворота, изгибающих моментов и поперечных сил изменяются, например, по линейному закону, можно вычислить их значение в точках между узлами. При этом зависимости (2)–(4) игнорируются.
 Чтобы учесть в промежуточных точках эти зависимости, следовало бы дискретную функцию прогибов Vi(zi), определенную в узлах расчетной сеточной области, аппроксимировать и получить аналитическую функцию прогибов V(z). А затем, пользуясь соотношениями (2)–(4), получить аналитические выражения для функций углов поворота, изгибающих моментов и поперечных сил. Эту процедуру можно значительно упростить, если воспользоваться программно-математическим обеспечением персональных компьютеров, в частности, математическим пакетом MathCAD, который чрезвычайно прост в использовании и легок в изучении [4]. Большинство действий, необходимых для управления программой, являются интуитивно прозрачными. Однако большинство встроенных функций MathCAD вычисляются приближенно, причем процедура их вычисления скрыта от пользователя. Это может привести к неожиданным результатам при решении конкретных задач.
Чтобы учесть в промежуточных точках эти зависимости, следовало бы дискретную функцию прогибов Vi(zi), определенную в узлах расчетной сеточной области, аппроксимировать и получить аналитическую функцию прогибов V(z). А затем, пользуясь соотношениями (2)–(4), получить аналитические выражения для функций углов поворота, изгибающих моментов и поперечных сил. Эту процедуру можно значительно упростить, если воспользоваться программно-математическим обеспечением персональных компьютеров, в частности, математическим пакетом MathCAD, который чрезвычайно прост в использовании и легок в изучении [4]. Большинство действий, необходимых для управления программой, являются интуитивно прозрачными. Однако большинство встроенных функций MathCAD вычисляются приближенно, причем процедура их вычисления скрыта от пользователя. Это может привести к неожиданным результатам при решении конкретных задач.
Пакет MathCAD позволяет аппроксимировать дискретное множество значений (x, y) при помощи нескольких встроенных функций [5, 6]. Для линейной интерполяции используется функция linterp(x, y, t), которая представляет искомую аппроксимирующую функцию в виде ломаной линии. Аппроксимация при помощи кубической сплайн-интерполяции выполняется с использованием функции interp(s, x, y, t), где s – вектор вторых производных, созданный одной из сопутствующих функций: lspline(x, y) – вектор значений коэффициентов линейного сплайна, pspline(x, y) – вектор значений коэффициентов квадратичного сплайна, cspline(x, y) – вектор значений коэффициентов кубического сплайна. Следует отметить, что сопутствующие функции существенно влияют на поведение аппроксимирующей функции, особенно вблизи граничных точек рассматриваемого интервала, что приводит к значительной разнице в поведении аппроксимирующей функции при ее экстраполяции за его пределами. Полиномиальная сплайн-интерполяция (интерполяция при помощи В-сплайнов) использует функцию interp(s, x, y, t), где s – вектор вторых производных, созданный функцией bspline(x, y, u, n), вычисляющей вектор значений коэффициентов В-сплайна.
При попытке использования встроенных аппроксимирующих функций математического пакета MathCAD даже при решении простейшей задачи сопротивления материалов о плоском поперечном изгибе стержня, шарнирно закрепленного по концам и нагруженного равномерно распределенной нагрузкой интенсивности q, возникают некоторые проблемы, говорящие о необходимости исключения формального подхода к построению решения задач с использованием «черных ящиков». А ведь для пользователя математический пакет MathCAD и есть типичный «черный ящик» [7].
Рассмотрим решение задачи о плоском поперечном изгибе стержня, шарнирно закрепленного по концам и нагруженного равномерно распределенной нагрузкой интенсивности q (рис. 1). Данная краевая задача имеет аналитическое решение:
 (5)
(5)
Из формул (5) видно, что прогиб стержня описывается кривой 4-го порядка, угол поворота поперечного сечения – кривой 3-го порядка, изгибающий момент – кривой 2-го порядка и поперечная сила – кривой 1-го порядка. Это означает, что при решении данной задачи методом конечных разностей аппроксимировать функцию поперечной силы между узлами расчетной сетки следует линейной функцией, в то время как функцию изгибающего момента – квадратной параболой, функцию угла поворота поперечного сечения – кубической параболой, а для аппроксимации функции прогибов между узлами необходимо использовать параболу четвертого порядка. Таким образом, предположение о линейном законе распределения функции прогибов, углов поворота, изгибающих моментов и поперечных сил между узлами является достаточно грубым приближением.
Исходные данные для задачи: стержень длиной l=6 м, выполненный из стали с модулем упругости E=215×109 Па и расчетным сопротивлением по нормальным напряжениям Rs=240×106 Па, имеет прямоугольное поперечное сечение размером b´h=0,05´0,20 м. Коэффициент надежности по нагрузке gf=1,12, коэффициент условий работы gc=0,96. Величина расчетной нагрузки из условия прочности по нормальным напряжениям составляет  ; нормативная нагрузка
; нормативная нагрузка  . Максимальные величины прогиба, угла поворота, изгибающего момента и поперечной силы на основании соотношений (5) будут следующими (по абсолютной величине):
. Максимальные величины прогиба, угла поворота, изгибающего момента и поперечной силы на основании соотношений (5) будут следующими (по абсолютной величине):

Значения среднеквадратичных отклонений между соответствующими функциями прогиба, угла поворота, изгибающего момента и поперечной силы, вычисленными по формулам (5) и вычисленными методом конечных разностей на интервале l=6 м с шагом D=0,5 м:
DVср=1,282×10–4 м; Djср=7,595×10–5; (6)
DMср=7,586×10–10 Нм; DQср=6,226×10–10 Н.
Теперь найдем аналитическое выражение сеточной функции прогибов V(z), то есть функции прогибов, полученной методом конечных разностей, при помощи кубической сплайн-интерполяции – функции interp(s, x, y, t), используя сопутствующую функцию lspline(x, y) для коэффициентов линейного сплайна. Для вычисления функции углов поворота j(z), изгибающих моментов Mx(z), поперечных сил Qy(z) воспользуемся соотношениями (2)–(4). Значения среднеквадратичных отклонений между соответствующими функциями прогиба, угла поворота, изгибающего момента и поперечной силы, вычисленными при помощи кубической сплайн-интерполяции и вычисленными
– по формулам (5):
DVср=1,282×10–4 м; Djср=7,372×10–5; (7)
DMср=559,134 Нм; DQср=820,81 Н;
– методом конечных разностей:
DVср=0,0 м; Djср=1,496×10–4; (8)
DMср=559,134 Нм; DQср=820,81 Н.
На рисунке 2 показаны эпюры прогибов (а), углов поворота (б), изгибающих моментов (в) и поперечных сил (г), построенных на интервале [–2, 8] метров, включающем область решения задачи [0, 6] метра.
На рисунках 2–5 сплошная линия построена при помощи кубической сплайн-интерполяции и формул (2)–(4), круглые маркеры отображают решение, построенное методом конечных разностей.
Теперь найдем аналитическое выражение сеточной функции прогибов V(z), полученной методом конечных разностей, при помощи кубической сплайн-интерполяции – функции interp(s, x, y, t), используя сопутствующую функцию pspline(x, y) для коэффициентов квадратичного сплайна. Для вычисления функции углов поворота j(z), изгибающих моментов Mx(z) и поперечных сил Qy(z) вновь воспользуемся соотношениями (2)–(4). Значения среднеквадратичных отклонений между соответствующими функциями прогиба, угла поворота, изгибающего момента и поперечной силы, вычисленными при помощи кубической сплайн-интерполяции и вычисленными
– по формулам (5):
DVср=1,282×10–4 м; Djср=1,747×10–4; (9)
DMср=6,365×103 Нм; DQср=1,74×104 Н;
– методом конечных разностей:
DVср=0,0 м; Djср=2,391×10–4; (10)
DMср=6,365×10–3 Нм; DQср=1,74×104 Н.
На рисунке 3 показаны эпюры прогибов (а), углов поворота (б), изгибающих моментов (в) и поперечных сил (г), построенных на интервале [–2, 8] метров, включающем область решения задачи [0, 6] метра.
Далее найдем аналитическое выражение сеточной функции прогибов V(z), полученной методом конечных разностей, при помощи кубической сплайн-интерполяции – функция interp(s, x, y, t), используя сопутствующую функцию cspline(x, y) для коэффициентов кубического сплайна. Для вычисления функции углов поворота j(z), изгибающих моментов Mx(z) и поперечных сил Qy(z) снова воспользуемся соотношениями (2)–(4). Значения среднеквадратичных отклонений между соответствующими функциями прогиба, угла поворота, изгибающего момента и поперечной силы, вычисленными при помощи кубической сплайн-интерполяции и вычисленными
– по формулам (5):
DVср=1,282×10–4 м; Djср=8,618×10–5; (11)
DMср=1,195×103 Нм; DQср=3,624×103 Н;
– методом конечных разностей:
DVср=0,0 м; Djср=1,615×10–4; (12)
DMср=1,195×103 Нм; DQср=3,624×103 Н.
На рисунке 4 показаны эпюры прогибов (а), углов поворота (б), изгибающих моментов (в) и поперечных сил (г), построенных на интервале [–2, 8] метров, включающем область решения задачи [0, 6] метра.


 Как уже указывалось ранее в [5], поведение аппроксимирующих кривых существенно разнится на границах рассматриваемого интервала и зависит от вида сопутствующей функции. Ввиду этого возникло предположение, что решение задачи может улучшиться, если функцию, аппроксимирующую сеточную функцию перемещений V(z), экстраполировать функцией предсказаний predict(y, m, n) за пределы рассматриваемого интервала вправо и влево.
Как уже указывалось ранее в [5], поведение аппроксимирующих кривых существенно разнится на границах рассматриваемого интервала и зависит от вида сопутствующей функции. Ввиду этого возникло предположение, что решение задачи может улучшиться, если функцию, аппроксимирующую сеточную функцию перемещений V(z), экстраполировать функцией предсказаний predict(y, m, n) за пределы рассматриваемого интервала вправо и влево.
Приведем результаты решения рассматриваемой задачи для случая, когда функция перемещений V(z) экстраполируется вправо и влево на четыре шага при помощи функции предсказаний predict(y, m, n). При этом количество последовательных элементов вектора  , согласно которым строится экстраполяция, принималось равным половине количества узлов расчетной сетки.
, согласно которым строится экстраполяция, принималось равным половине количества узлов расчетной сетки.
Как показали численные расчеты, среднеквадратичные отклонения между соответствующими функциями прогиба, угла поворота, изгибающего момента и поперечной силы, вычисленными по формулам (2)–(4), для аналитической функции прогибов V(z), полученной при помощи кубической сплайн-интерполяции с использованием функции предсказаний, и вычисленными по формулам (5) и методом конечных разностей, не зависят от вида сопутствующей функции. Значения среднеквадратичных отклонений:
– при использовании формул (5):
DVср=1,282×10–4 м; Djср=7,894×10–5; (13)
DMср=719,008 Нм; DQср=1,892×103 Н;
– при использовании метода конечных разностей:
DVср=0,0 м; Djср=1,548×10–4; (14)
DMср=719,008 Нм; DQср=1,892×103 Н.
На рисунке 5 в качестве иллюстрации пока- заны эпюры прогибов (а), углов поворота (б), изгибающих моментов (в) и поперечных сил (г), построенные на интервале [–2, 8] метров, включающем область решения задачи [0, 6] метра. Аналитическая функция прогибов  получена при помощи кубической сплайн-интерполяции с использованием сопутствующей функции для коэффициентов кубического сплайна и экстраполирована функцией предсказаний вправо и влево на четыре шага.
получена при помощи кубической сплайн-интерполяции с использованием сопутствующей функции для коэффициентов кубического сплайна и экстраполирована функцией предсказаний вправо и влево на четыре шага.
Анализируя полученные результаты решения задачи об изгибе стержня, отметим следующее.
· Среднеквадратичное отклонение функции прогибов, вычисленной при помощи кубической сплайн-интерполяции и вычисленной методом конечных разностей, во всех случаях равно нулю (8, 10, 12, 14).
· Среднеквадратичное отклонение функции прогибов, вычисленной при помощи кубической сплайн-интерполяции и вычисленной аналитически по формулам (5), во всех случаях равно DVср=1,282×10–4 м (7, 9, 11, 13).
· Среднеквадратичные отклонения функций углов поворота, изгибающих моментов и поперечных сил, вычисленных при помощи кубической сплайн-интерполяции с использованием линейного сплайна без использования функции предсказания, меньше среднеквадратичных отклонений, вычисленных при помощи кубической сплайн-интерполяции с использованием линейного сплайна и функции предсказания.
·  Среднеквадратичные отклонения функций углов поворота, изгибающих моментов и поперечных сил, вычисленных при помощи кубической сплайн-интерполяции с использованием квадратичного и кубического сплайнов без использования функции предсказания, больше среднеквадратичных отклонений, вычисленных при помощи кубической сплайн-интерполяции с использованием квадратичного и кубического сплайнов и функции предсказания.
Среднеквадратичные отклонения функций углов поворота, изгибающих моментов и поперечных сил, вычисленных при помощи кубической сплайн-интерполяции с использованием квадратичного и кубического сплайнов без использования функции предсказания, больше среднеквадратичных отклонений, вычисленных при помощи кубической сплайн-интерполяции с использованием квадратичного и кубического сплайнов и функции предсказания.
· Среднеквадратичные отклонения функций углов поворота, изгибающих моментов и поперечных сил, вычисленных при помощи кубической сплайн-интерполяции с использованием квадратичного сплайна без использования функции предсказания, оказались наибольшими.
· Среднеквадратичные отклонения функций углов поворота, изгибающих моментов и поперечных сил, вычисленных при помощи кубической сплайн-интерполяции с использованием линейного сплайна без использования функции предсказания, оказались наименьшими.
· Среднеквадратичные отклонения функций углов поворота, изгибающих моментов и поперечных сил, вычисленных при помощи кубической сплайн-интерполяции с использованием функции предсказания, не зависят от вида сопутствующей функции.
· Вид эпюры поперечных сил, построенной по формуле (4), существенно зависит от точности построения, причем, чем больше шаг вычислений, тем более гладкой получается кривая; для малого шага вычислений кривая Q(z) представляется набором прямых, параллельных оси абсцисс и соединенных наклонными отрезками в узлах конечно-разностной сетки (при построении аппроксимирующих кривых шаг принят равным 0,1).
· Независимо от вида кривой Q(z) значение поперечной силы на участке между узлами конечно-разностной сетки остается постоянным, что соответствует ступенчатой функции.
· Вычисление изгибающего момента и поперечной силы с использованием первой производной, то есть  и
и  , приводит к потере данных и невозможности вычисления функции поперечной силы Qy(z).
, приводит к потере данных и невозможности вычисления функции поперечной силы Qy(z).
На основании изложенного можно сделать вывод о том, что наиболее приемлемой встроенной аппроксимирующей функцией математического пакета MathCAD при решении задач механики деформируемого твердого тела, когда искомые параметры задачи выражаются одно через другое при помощи производных, является кубическая сплайн-интерполяция кубическим сплайном с использованием функции предсказания. Результаты работы могут найти применение при численном решении задач механики деформируемого твердого тела.
Литература
1. Александров А.В., Потапов В.Д. Сопротивление материалов. Основы теории упругости и пластичности. Изд. 2-е. М.: Высшая школа, 2002. 400 с.
2. Потапов В.Д., Александров А.В., Косицын С.Б., Долотказин Д.Б. Строительная механика: В 2 кн. Кн. 1. Статика упругих систем: учеб. для вузов. М.: Высш. шк., 2007. 511 с.
3. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. Изд. 3-е. М.: Высш. шк., 2003. 560 с.
4. Бакушев С.В. Компьютерные технологии решения задач в архитектурно-строительном вузе // Смешанное и корпоративное обучение («СКО-2007»): тр. Всерос. науч.-метод. симпоз. Р-н-Д: Изд-во ИПО ПИ ЮФУ, 2007. С. 110–113.
5. Кирьянов Д.В. Самоучитель Mathcad 12. СПб: БХВ-Петербург, 2004. 576 с.
6. Макаров Е.Г. Инженерные расчеты в MathCAD: учеб. курс. СПб: Питер, 2005. 448 с.
7. Бакушев С.В. «Черные ящики» и образовательный процесс // Современное состояние и перспективы развития строительной отрасли: сб. науч. тр. Междунар. науч. конф. Пенза: Изд-во ПГУАС, 2011. С. 269–275.



 . (1)
. (1)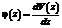 . (2)
. (2) . (3)
. (3) . (4)
. (4)
 (5)
(5) ; нормативная нагрузка
; нормативная нагрузка  . Максимальные величины прогиба, угла поворота, изгибающего момента и поперечной силы на основании соотношений (5) будут следующими (по абсолютной величине):
. Максимальные величины прогиба, угла поворота, изгибающего момента и поперечной силы на основании соотношений (5) будут следующими (по абсолютной величине):



 , согласно которым строится экстраполяция, принималось равным половине количества узлов расчетной сетки.
, согласно которым строится экстраполяция, принималось равным половине количества узлов расчетной сетки. получена при помощи кубической сплайн-интерполяции с использованием сопутствующей функции для коэффициентов кубического сплайна и экстраполирована функцией предсказаний вправо и влево на четыре шага.
получена при помощи кубической сплайн-интерполяции с использованием сопутствующей функции для коэффициентов кубического сплайна и экстраполирована функцией предсказаний вправо и влево на четыре шага.
 и
и  , приводит к потере данных и невозможности вычисления функции поперечной силы Qy(z).
, приводит к потере данных и невозможности вычисления функции поперечной силы Qy(z).