Любому спортивному соревнованию по игровым видам спорта предшествует кропотливый и достаточно трудоемкий подготовительный этап проведения жеребьевки. Целью жеребьевки является формирование турнирной таблицы. Особое значение это имеет для тех видов спорта, в которых принимают участие большое количество игроков из разных регионов. В этих случаях необходимо рассеять игроков по разным группам таким образом, чтобы все группы имели примерно одинаковый суммарный рейтинг, то есть были равными по силам, и при этом в каждую из них входили игроки из разных регионов. Ситуация зна- чительно усложняется, когда от одного региона заявки на участие в турнире поданы несколькими его представителями. Таких участников необходимо распределить в различные отборочные группы [1].
Таким образом, задача становится двухкритериальной: первый критерий – суммарный рейтинг групп (он должен быть по возможности одинаковым), второй критерий – распределение участников турнира из одного региона по группам (оно должно быть равномерным). Решение этой задачи уже требует специфичных алгоритмов. Такая ситуация типична, в частности, для настольного тенниса.
Формально задачу жеребьевки можно свести к известной математической задаче разбиения графа на подграфы, каждый из которых будет соответствовать одной из групп в турнирной таблице. Каждая вершина графа имеет вес, характеризующий рейтинг определенного участника. Ребра графа отображают отношения между участниками: наличие ребра говорит о том, что соответствующие участники являются представителями одной ассоциации или клуба. Пример графовой модели данной задачи приведен на рисунке 1.
 Такой граф является симметричным, при этом число его компонент равно числу ассоциаций (клубов). Причем каждая компонента является кликой графа, то есть полносвязным подграфом, и при этом выполняется условие транзитивности: если A и B – одноклубники, A и C – одноклубники, то B и C также являются одноклубниками. Математическая модель задачи определяется матрицей смежности графа D=úçdijúç и вектором P = {p1, p2, …, pn}, где pi – рейтинг участника, а dij = 1, если участник с номером i является одноклубником участника под номером j, иначе dij = 0. Цель данной задачи разбиения – получить такие непересекающиеся подграфы (то есть когда одна вершина может принадлежать только одному подграфу), в которых число внутренних связей между вершинами было бы минимальным или, соответственно, число внешних связей максимальным. Такая постановка задачи отличается от типичной задачи разбиения графа на подграфы [2–4], поскольку в типовом случае решается задача с противоположной целевой функцией – минимизируется внешнее число связей между подграфами. Приведенные соображения обусловили целесообразность рассмотрения подходов и приемов, используемых сейчас в реальных случаях неавтоматизированного проведения жеребьевки, и по возможности выявления тех из них, которые могут лечь в основу построения эффективных алгоритмов автоматизированного формирования турнирных таблиц.
Такой граф является симметричным, при этом число его компонент равно числу ассоциаций (клубов). Причем каждая компонента является кликой графа, то есть полносвязным подграфом, и при этом выполняется условие транзитивности: если A и B – одноклубники, A и C – одноклубники, то B и C также являются одноклубниками. Математическая модель задачи определяется матрицей смежности графа D=úçdijúç и вектором P = {p1, p2, …, pn}, где pi – рейтинг участника, а dij = 1, если участник с номером i является одноклубником участника под номером j, иначе dij = 0. Цель данной задачи разбиения – получить такие непересекающиеся подграфы (то есть когда одна вершина может принадлежать только одному подграфу), в которых число внутренних связей между вершинами было бы минимальным или, соответственно, число внешних связей максимальным. Такая постановка задачи отличается от типичной задачи разбиения графа на подграфы [2–4], поскольку в типовом случае решается задача с противоположной целевой функцией – минимизируется внешнее число связей между подграфами. Приведенные соображения обусловили целесообразность рассмотрения подходов и приемов, используемых сейчас в реальных случаях неавтоматизированного проведения жеребьевки, и по возможности выявления тех из них, которые могут лечь в основу построения эффективных алгоритмов автоматизированного формирования турнирных таблиц.
Способы проведения жеребьевки
В практике проведения турниров по игровым видам спорта сложились определенные подходы к проведению жеребьевки. Как и в большинстве видов спорта, в настольном теннисе при большом числе участников сначала проводится отборочный турнир. Для этого участники рассеиваются в несколько отборочных групп. Иногда этот процесс называют посевом. Посев может осуществляться различными способами: случайно, зигзагом, змейкой [5].
Традиционные способы жеребьевки. Самым распространенным способом является посев змейкой. Формально он осуществляется следующим образом. Сначала все игроки упорядочиваются по рейтингу. Затем, начиная с игрока с наивысшим рейтингом, последовательно по мере убывания рейтинга игроков их атрибутами (данными об игроках) заполняются первые m позиций, начиная с 1-й по m-ю группу. Следующими по рейтингу m игроками продолжают заполнение вторых позиций во всех группах, начиная с m-й группы и заканчивая 1-й группой. Очередными m игроками продолжают заполнение третьих позиций во всех группах, снова начиная с 1-й группы и заканчивая m-й группой. Такой посев змейкой продолжают до тех пор, пока не заполнятся все позиции во всех группах.
Формально, используя понятие инверсных (обратных) чисел, нетрудно показать, что при понижении рейтингов участников от максимального до минимального на постоянную величину суммарные рейтинги всех групп будут одинаковыми. Для простоты будем считать, что имеется некоторая ограниченная убывающая последовательность натуральных чисел R = {r1, r2, …, rk}. Для любого числа rÎR этой последовательности существует инверсное число  , определяемое следующим образом:
, определяемое следующим образом:  = r1+rk–r. (1)
= r1+rk–r. (1)
В соответствии с формулой (1) любую нечетную и четную пару строк турнирной таблицы с записанными в ее ячейки рейтингами в общем виде можно представить в виде развертки удвоенной длины (рис. 2). В данном случае величина m – число групп.
Складывая попарно каждое прямое и инверсное число, будем получать одну и ту же величину. Аналогичным образом каждая последующая пара строк турнирной таблицы при сложении прямого и соответствующего инверсного числа также будет давать одну и ту же величину. В итоге это приведет к тому, что сумма всех чисел (рейтингов) во всех столбцах будет одна и та же.
Наибольшая применимость посева змейкой объясняется тем, что, используя эту эвристику, удается формировать примерно одинаковые по силе группы. Это также обеспечивает снижение вероятности раннего выбывания из турнира сильных участников и дальнейшего продвижения к финалу слабых.
 Нетрадиционные способы жеребьевки. Традиционные способы жеребьевки не исключают применение других, нетрадиционных способов. При малом числе участников можно использовать способ, основанный на полном переборе вариантов формирования отборочных групп. Такой способ является точным в математическом смысле, поскольку с его помощью рассматриваются всевозможные варианты, из которых можно выбрать наилучшие, удовлетворяющие выбранным критериям качества сформированных групп. Множество всех вариантов в данном случае представляет всевозможные комбинаторные распределения участников по разным группам. Нетрудно показать, что число таких распределений будет представлять величину
Нетрадиционные способы жеребьевки. Традиционные способы жеребьевки не исключают применение других, нетрадиционных способов. При малом числе участников можно использовать способ, основанный на полном переборе вариантов формирования отборочных групп. Такой способ является точным в математическом смысле, поскольку с его помощью рассматриваются всевозможные варианты, из которых можно выбрать наилучшие, удовлетворяющие выбранным критериям качества сформированных групп. Множество всех вариантов в данном случае представляет всевозможные комбинаторные распределения участников по разным группам. Нетрудно показать, что число таких распределений будет представлять величину
 , (2)
, (2)
где n – число всех участников турнира; m – количество групп; ki – количество участников в i-й группе.
Например, в соответствии с формулой (2), при распределении 6 участников по 3 в 2 группы получаем Q(6, 2) = 10, а по 2 участника в 3 группы – Q(6, 3) = 15. При таком числе участников число вариантов их распределений по группам представляет малую величину и задачу можно решить точно полным перебором. Однако при распределении реального числа участников, например 16 по 4 группам, число вариантов резко увеличивается и представляет величину Q(16, 4) = 2627625. Для такого числа вариантов полный перебор еще возможен. Но для другого, также реального случая, когда 24 участника распределяются в 4 группы по 6 участников в каждой, получаем уже огромное число вариантов – Q(24, 4) > 9,6·1010. Осуществить полный перебор такого числа вариантов даже на суперсовременном компьютере невозможно. Ситуацию не спасают и параллельные вычисления [6] как по экономическим, так и по техническим причинам, наталкиваясь на ограничения в соответствии с законом Амдала [7]. Отсюда следует, что только в случае, если число участников турнира не превышает 16, задачу можно решать полным перебором. Алгоритмы формирования различных комбинаторных соединений достаточно хорошо разработаны и описаны, например в [8, 9].
Однако, как отмечалось выше, в общем случае задача жеребьевки является двухкритериальной. Если первый критерий – суммарный рейтинг игроков группы – легко подсчитывается, то второй – равномерность распределения игроков, представляющих одну ассоциацию, требует некоторых размышлений. Логично предположить, что одним из худших случаев будет такой, когда в группы попадают игроки из одной ассоциации, а лучшим – когда игроки из одной ассоциации рассредоточены по разным группам. Исходя из этих крайних случаев, этот критерий (назовем его критерием равномерности (Кр)) предлагается рассчитывать следующим образом: числа одинаковых ассоциаций в группе возводятся в квадрат и суммируются. Полученные таким же образом результаты во всех группах также суммируются, и общий результат всех суммирований делится на число групп. Таким образом, формула подсчета критерия равномерности будет иметь вид 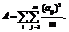
В приведенной формуле aij определяет число i-й ассоциации в группе j. Число aij возводится в квадрат, поскольку только в этом случае просуммированные разные ассоциации в группе дают наименьшую величину, равную n. Если же одной и той же ассоциации в группе будет больше одной, возведение таких чисел в квадрат и их суммирование приводят к превышению этой величины. Так, например, если в каждую из m групп входят n игроков из одной ассоциации (худший случай), то A1=mn2. Если же в каждую группу входят игроки из разных ассоциаций (лучший случай), то A2=mn

Цифры в строках 1–3 этих таблиц означают номера регионов, цифры в их последних строках определяют критерий равномерности распределения игроков в группах. Для каждой группы они получаются как сумма квадратов числа одинаковых регионов. Так, в таблице 1 в каждой группе все три игрока представляют один регион, поэтому равномерность во всех трех группах равна 32. В таблице 2 каждую группу представляют игроки из разных регионов, поэтому равномерность каждой группы равна 3. Очевидно, что турнирная таблица 1 с точки зрения равномерности распределения игроков представляет наихудший случай, а таблица 2 – наилучший. Ясно и то, что о равномерности нужно судить не по одной группе, а по всем, то есть использовать усредненное значение по всем группам.
Для полноты анализа критерия равномерности в таблице 3 приведем некоторые примеры возможных распределений в турнирной таблице игроков из разных регионов.
Визуальный анализ не противоречит приведенным подсчетам: при критерии равномерности Кр = 11,5 в двух группах (Гр.1 и Гр.2) игроки только из одного региона, а при критерии равномерности Кр = 6,5 игроки по группам распределены в таблице существенно равномернее. Показатели турнирной таблицы при критериях равномерности Кр = 7,5 и Кр = 9 занимают промежуточное положение.
Построение компромиссной аддитивной целевой функции. Для решения двухкритериальной задачи формирования турнирных таблиц полным перебором (при условии небольшого числа игроков) нужно иметь компромиссную аддитивную целевую функцию (ЦФ), содержащую оба эти критерия. К компромиссным ЦФ предъявляется ряд требований [10, 11]. Входящие в ЦФ параметры имеют, как правило, различные размерности, поэтому их необходимо привести к безразмерным величинам. В аддитивную ЦФ каждый параметр должен входить с соответствующим весовым коэффициентом важности, определяющим компромисс ЦФ. Улучшающие ЦФ параметры должны входить в нее со знаком плюс, ухудшающие – со знаком минус.
|
Таблица 3
Турнирные таблицы с разными критериями равномерности
Table 3
The standings with different uniformity criteria
|
|
Гр.1
|
Гр.2
|
Гр.3
|
Гр.4
|
|
Кр = 6,5
|
|
1
|
3
|
4
|
2
|
|
2
|
1
|
4
|
3
|
|
3
|
4
|
3
|
4
|
|
3
|
2
|
4
|
4
|
|
6
|
4
|
10
|
6
|
|
Кр = 7,5
|
|
1
|
1
|
2
|
3
|
|
2
|
4
|
4
|
3
|
|
3
|
4
|
3
|
3
|
|
4
|
4
|
4
|
2
|
|
4
|
10
|
6
|
10
|
|
Кр = 9
|
|
1
|
4
|
4
|
2
|
|
2
|
4
|
3
|
2
|
|
3
|
4
|
3
|
3
|
|
4
|
4
|
3
|
1
|
|
4
|
16
|
10
|
6
|
|
Кр = 11,5
|
|
3
|
4
|
3
|
2
|
|
3
|
4
|
4
|
2
|
|
3
|
4
|
4
|
1
|
|
3
|
4
|
2
|
1
|
|
16
|
16
|
6
|
8
|
Безразмерное значение параметра pk обеспечивается введением нормирующей величины pkн, а степень компромисса назначается с помощью коэффициентов ak£1. Значение нормирующей величины pkн можно назначить различными способами. Лучшим является способ, если нормирующую величину можно определить априорно как наилучшее ее значение из всех возможных. Если параметр pk входит в ЦФ как уменьшающий ее значение, в качестве нормирующей величины этого параметра нужно выбирать теоретически минимальное его значение. Если же параметр pk входит в ЦФ как увеличивающий ее значение, в качестве нормирующей величины этого параметра нужно выбирать теоретически максимальное его значение.
Предлагается следующий вид компромиссной ЦФ:
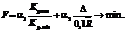 (3)
(3)
Здесь Kр.тек – текущий критерий равномерности; Kр.min – минимальный нормирующий критерий равномерности, определяемый априорно (детальное обоснование его величины приведено в [12]); D=Rmax–Rmin (Rmax, Rmin – соответственно наибольший и наименьший суммарные рейтинги групп);  – среднее значение суммарного рейтинга групп; a1 и a2 – важность критериев, устанавливаемых экспертами.
– среднее значение суммарного рейтинга групп; a1 и a2 – важность критериев, устанавливаемых экспертами.
Приведенную ЦФ можно использовать при построении оптимальной турнирной таблицы методом полного перебора вариантов двумя способами. При первом (стандартном) способе после формирования очередного варианта турнирной таблицы по формуле (3) подсчитывается ЦФ и ее значение сравнивается с предыдущим значением ЦФ, хранящимся в памяти. Если очередное значение ЦФ меньше предыдущего, то ее значение и соответствующий ей вариант турнирной таблицы замещают в памяти предыдущий вариант турнирной таблицы. После перебора всех вариантов турнирной таблицы в памяти будет сохранен лучший ее вариант.
При втором способе один из составляющих критериев компромиссной ЦФ (3) нужно сделать ограничением, то есть коэффициент веса при этом критерии приравняем к нулю. Тогда ЦФ станет однокритериальной и при переборе вариантов турнирной таблицы оптимизация будет осуществляться только по другому критерию, но при условии, что значение первого критерия не будет выходить за установленные пределы.
Для демонстрации пригодности построенной ЦФ (3) к оптимизации турнирных таблиц рассмотрим два их гипотетических варианта. Пусть число игроков N = 16 и представляют они 4 различных региона, которые в турнирных таблицах будем помечать цифрами 1, 2, 3 и 4 через запятую после рейтинга игрока. Рассмотрим два крайних случая турнирной таблицы: лучший (табл. 4) и худший (табл. 5).
|
Таблица 4
Лучший гипотетический случай
Table 4
The best hypothetical case
|
|
Таблица 5
Худший гипотетический случай
Table 4
The worst hypothetical case
|
|
Гр.1
|
Гр.2
|
Гр.3
|
Гр.4
|
|
Гр.1
|
Гр.2
|
Гр.3
|
Гр.4
|
|
40,1
|
36,1
|
33,1
|
30,1
|
40,1
|
23,1
|
18,2
|
8,3
|
|
23,1
|
24,1
|
27,1
|
29,1
|
36,1
|
24,1
|
17,2
|
10,3
|
|
20,1
|
18,2
|
17,2
|
14,2
|
33,1
|
27,1
|
14,2
|
12,4
|
|
8,3
|
10,3
|
12,4
|
13,4
|
30,1
|
29,1
|
20,1
|
13,4
|
|
91,10
|
88,6
|
89,6
|
86,6
|
139,16
|
103,16
|
69,10
|
43,8
|
В последних строках таблиц 4 и 5 для каждой группы указан суммарный рейтинг, а через запятую – критерий равномерности. Полагая весовые коэффициенты важности обоих критериев равными a1=a2=0,5, рассчитаем ЦФ F1 для таблицы 4 и F2 для таблицы 5. Для таблицы 4 D=5, а минимальный и расчетный (текущий) критерии равномерности совпадают, то есть Kр.тек = Kр.min =28/4=7.
Для таблицы 5 D=96, а текущий критерий равномерности будет Kр.тек=(16+16+10+8)/4=12,5.
Подставив эти значения в формулу (3), получим значения F1 = 0,78, F2 = 6,29. Видим, что для лучшего варианта турнирной таблицы наша ЦФ минимальна, а для худшего случая максимальна. Таким образом, как и предполагалось, построенная двухкритериальная ЦФ является валидной, то есть соответствует своему предназначению.
Другой способ нетрадиционной жеребьевки можно использовать, опираясь на работу [13], в которой рассмотрен последовательный алгоритм распределения вопросов изучаемой дисциплины по тестовым заданиям. Число тестовых заданий можно рассматривать как число групп в нашем случае, а число вопросов в тестовом задании – как число игроков в группе.
Сначала вычисляется средний суммарный рейтинг, общий для всех групп, по формуле  а потом начинается последовательное формирование групп на основе следующей эвристики. Полагая, что в первые позиции каждой группы посеяны игроки с максимальными рейтингами, в очередную группу на i-м шаге распределяется тот игрок, рейтинг которого меньше всего отличается от величины, определяемой по формуле
а потом начинается последовательное формирование групп на основе следующей эвристики. Полагая, что в первые позиции каждой группы посеяны игроки с максимальными рейтингами, в очередную группу на i-м шаге распределяется тот игрок, рейтинг которого меньше всего отличается от величины, определяемой по формуле  , где N – общее количество игроков; gi–1 – сумма рейтингов игроков, уже распределенных в рассматриваемую группу, и рассчитываемая по формуле
, где N – общее количество игроков; gi–1 – сумма рейтингов игроков, уже распределенных в рассматриваемую группу, и рассчитываемая по формуле 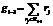 , где Ri–1 – множество игроков с рейтингами, распределенных в рассматриваемую группу к (i–1)-му шагу. Таким образом, значение величины
, где Ri–1 – множество игроков с рейтингами, распределенных в рассматриваемую группу к (i–1)-му шагу. Таким образом, значение величины  определяет того игрока, рейтинг которого наиболее подходит для включения в формируемую на i-м шаге группу.
определяет того игрока, рейтинг которого наиболее подходит для включения в формируемую на i-м шаге группу.
Предтурнирный анализ задачи жеребьевки
Одним из важных вопросов, решаемых до проведения турнира, является вопрос о количестве отборочных групп и числе участников в группе. Это зависит от общего числа игроков. Поскольку в группах каждый участник турнира играет с каждым, число игр в группе определяется как число сочетаний из n по 2, то есть по формуле  , где n – число игроков в группе. Например, при общем числе игроков N = 24 наиболее типичной является турнирная таблица, состоящая из 6 групп по 4 игрока в каждой группе или из 4 групп по 6 игроков. В первом случае необходимо провести всего 6 игр в каждой группе, во втором – 15. Ввиду того, что каждая игра состоит из 3, 5 или 7 партий, общее время проведения турнира необходимо увеличить в соответствующее число раз. Исходя из приведенного выше концептуального описания возможных вариантов жеребьевки, было принято решение о целесообразности построения алгоритма и его програм- мной реализации, опираясь на эвристику змейки.
, где n – число игроков в группе. Например, при общем числе игроков N = 24 наиболее типичной является турнирная таблица, состоящая из 6 групп по 4 игрока в каждой группе или из 4 групп по 6 игроков. В первом случае необходимо провести всего 6 игр в каждой группе, во втором – 15. Ввиду того, что каждая игра состоит из 3, 5 или 7 партий, общее время проведения турнира необходимо увеличить в соответствующее число раз. Исходя из приведенного выше концептуального описания возможных вариантов жеребьевки, было принято решение о целесообразности построения алгоритма и его програм- мной реализации, опираясь на эвристику змейки.
Формулировка задачи автоматизированного построения турнирной таблицы
Пусть задано множество S = {s1, s2, …, sn} игроков и число групп m. Во все группы входит одинаковое число игроков, каждый игрок идентифицирован рейтингом и ассоциацией, которую он представляет. Необходимо разработать алгоритм и соответствующий программный код, распределяющий множество игроков S по m группам таким образом, чтобы суммарный рейтинг каждой группы имел минимальное отклонение от среднего значения. Кроме того, если некоторые ассоциации представлены несколькими игроками, то они должны быть распределены по позициям групп по возможности равномерно. Под позицией понимается строка в турнирной таблице.
Первым этапом алгоритма жеребьевки является сортировка игроков по убыванию их рейтинга. Для обеспечения равномерности распределения нескольких игроков из одной и той же ассоциации на каждом шаге распределения очередного игрока сравниваются ассоциации игроков всех вышестоящих позиций с ассоциацией данного игрока. Если число ассоциаций в вышестоящих позициях превышает определенную величину, то данный игрок пропускает эту позицию, и для него аналогичным образом ищутся последующие позиции.
Как показали предварительные эксперименты (ручного распределения при малом числе игроков), эта стратегия приводит к более равномерному распределению суммарного рейтинга по всем группам. Поэтому она и была выбрана для программной реализации алгоритма, блок-схема которого приведена на рисунке 3.
Результаты работы алгоритма жеребьевки на тестовых примерах
По приведенному на рисунке 3 алгоритму был разработан программный код на языке С# в среде разработки Microsoft Visual Studio 2012. Объем кода программы составляет 403 Кб. При реализации программы использовалась структура данных Dictionary. Это сложная структура, позволяющая обеспечить доступ к элементам по ключу. Ключом ее является строковый тип данных – название ассоциации. Главное свойство и достоинство словарей – быстрый поиск на основе ключей. Ключи преобразуются в хеш, ассоциируя хеш-код со значением. Это позволяет добавлять новые элементы без накладных расходов производительности программы, связанных с необхо- димостью смещения последующих элементов в памяти. Анализ приведенной на рисунке 3 блок-схемы дает следующую оценку временной сложности алгоритма (ВСА): O(n)=n×logn, где n – число участников соревнования. Такая оценка ВСА незначительно отличается от линейной, а алгоритмы с линейной ВСА являются наиболее быстродействующими.
Основные окна интерфейса программы и результаты ее работы приведены на рисунках 4 и 5. На рисунке 4 представлено основное окно программы, с помощью которого создается пустой шаблон турнирной таблицы, куда можно добавлять отдельных участников. Сюда же вводятся исходные данные об участниках турнира. На рисунке 5 приведена турнирная таблица (нижняя часть окна), сформированная по одному из множества тестовых вариантов исходных данных, представленных в верхней части окна (в ней поместились только игроки с последними номерами).

 В самом нижнем поле окна (рис. 5) приведено среднеквадратическое отклонение суммарного рейтинга всех групп. По его величине можно в определенной степени судить о качестве полученного решения, если сравнивать его для разных вариантов формирования турнирных таблиц. Приведенный пример является одним из множества протестированных. По нему осуществлялась отладка алгоритма и программы путем сравнения полученных результатов автоматического и ручного формирования турнирной таблицы. Эти резуль- таты полностью совпали на тестах малой размерности (до 20 участников). На тестах большей размерности (до 64) среднеквадратическое отклонение суммарных рейтингов каждой подгруппы, полученное описанным алгоритмом, меньше ручного расчета на 5–10 %.
В самом нижнем поле окна (рис. 5) приведено среднеквадратическое отклонение суммарного рейтинга всех групп. По его величине можно в определенной степени судить о качестве полученного решения, если сравнивать его для разных вариантов формирования турнирных таблиц. Приведенный пример является одним из множества протестированных. По нему осуществлялась отладка алгоритма и программы путем сравнения полученных результатов автоматического и ручного формирования турнирной таблицы. Эти резуль- таты полностью совпали на тестах малой размерности (до 20 участников). На тестах большей размерности (до 64) среднеквадратическое отклонение суммарных рейтингов каждой подгруппы, полученное описанным алгоритмом, меньше ручного расчета на 5–10 %.
В заключение отметим, что в статье продемонстрированы лишь некоторые возможности раз- работанного алгоритма и программного кода. Интерфейс программы позволяет добавлять и удалять отдельных игроков, их принадлежность к региону (ассоциации), возраст, Ф.И.О. тренера. По предварительным оценкам членов судейских коллегий некоторых региональных соревнований, разработанный программный продукт в основном удовлетворяет требованиям по качеству автоматически созданных турнирных таблиц. После доработки данного программного продукта для его привязки к существующим программным комплексам он позволит многократно сократить время формирования турнирных таблиц. Однако, чтобы программному продукту придать товарный вид, авторам были выданы некоторые замечания и рекомендации по его усовершенствованию: программа работает только с целыми значениями рейтингов, но на практике встречаются и дробные рейтинги; если до жеребьевки встречаются одинаковые рейтинги, их надо предварительно упорядочить случайным образом. В процессе тестирования были найдены крайне редко встречающиеся случаи, которые будут учтены в следующей версии программы. Авторы полагают, что высказанные замечания и пожелания можно легко устранить, что позволит довести разработанный программный продукт до коммерческого вида.
Литература
1. Пенов Г.Г., Александров А.В., Зубарь Я.С., Кизи- лов А.В., Мазаев К.М., Пономарев В.К. Настольный теннис: сб. матер. для судей. М., 2012.
2. Гладков Л.А., Гладкова Н.В., Бричеева Ю.В. Решение задачи компоновки схем ЭВА на основе выделения клик // Конгресс по интеллект. сист. и информ. технологиям «IS–IT 13»: сб. тр. В 4-х т. М.: Физматлит, 2013. Т. 3. С. 151–153.
3. Курейчик В.М., Кажаров А.А. Роевой интеллект в решении графовых задач // Междунар. конф. по мягким вычислениям и измерениям (SCM'2013): сб тр. СПб, 2013. С. 31–34.
4. Гладков Л.А., Шкурко В.А. Решение задачи разбиения графа на подграфы на основе генетического алгоритма // Конгресс по интеллект. сист. и информ. технологиям «IS–IT’14»: сб. тр. В 4-х т. М.: Физматлит, 2014. Т. 3. С. 142–146.
5. Как делать посев? URL: http://www.trating.ru/info/howto/index.htm#HowSeed (дата обращения: 25.11.2014).
6. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. СПб: БХВ-Петербург, 2004. 608 с.
7. Закон Амдала в реальном мире. URL: riki-koen.livejournal.com/75235.html (дата обращения: 25.11.2014).
8. Курейчик В.М., Глушань В.М., Щербаков Л.И. Комбинаторные аппаратные модели и алгоритмы в САПР. М.: Радио и связь, 1990. 216 с.
9. Липский В. Комбинаторика для программистов; [пер. с польск.]. М.: Мир, 1988. 213 с.
10. Курицкий Б.Я. Оптимизация вокруг нас. Л.: Машиностроение, 1989. 144 с.
11. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. М.: Дрофа, 2006. 175 с.
12. Глушань В.М. Критериальные особенности оптимального формирования турнирных таблиц // Конгресс по интеллектуальным системам и информационным технологиям «AIS–IT’14»: сб. тр. В 4-х т. М.: Физматлит, 2014. Т. 1. С. 506–512.
13. Глушань В.М., Липало Н.Н., Малютин В.А. Оптимизация тестовых заданий при контроле знаний // Вестн. Таганрогского гос. пед. ин-та: Естественные науки. 2007. № 1. С. 72–76.


 , определяемое следующим образом:
, определяемое следующим образом: 
 , (2)
, (2)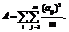

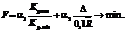 (3)
(3) – среднее значение суммарного рейтинга групп; a1 и a2 – важность критериев, устанавливаемых экспертами.
– среднее значение суммарного рейтинга групп; a1 и a2 – важность критериев, устанавливаемых экспертами. а потом начинается последовательное формирование групп на основе следующей эвристики. Полагая, что в первые позиции каждой группы посеяны игроки с максимальными рейтингами, в очередную группу на i-м шаге распределяется тот игрок, рейтинг которого меньше всего отличается от величины, определяемой по формуле
а потом начинается последовательное формирование групп на основе следующей эвристики. Полагая, что в первые позиции каждой группы посеяны игроки с максимальными рейтингами, в очередную группу на i-м шаге распределяется тот игрок, рейтинг которого меньше всего отличается от величины, определяемой по формуле  , где N – общее количество игроков; gi–1 – сумма рейтингов игроков, уже распределенных в рассматриваемую группу, и рассчитываемая по формуле
, где N – общее количество игроков; gi–1 – сумма рейтингов игроков, уже распределенных в рассматриваемую группу, и рассчитываемая по формуле 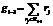 , где Ri–1 – множество игроков с рейтингами, распределенных в рассматриваемую группу к (i–1)-му шагу. Таким образом, значение величины
, где Ri–1 – множество игроков с рейтингами, распределенных в рассматриваемую группу к (i–1)-му шагу. Таким образом, значение величины  определяет того игрока, рейтинг которого наиболее подходит для включения в формируемую на i-м шаге группу.
определяет того игрока, рейтинг которого наиболее подходит для включения в формируемую на i-м шаге группу. , где n – число игроков в группе. Например, при общем числе игроков N = 24 наиболее типичной является турнирная таблица, состоящая из 6 групп по 4 игрока в каждой группе или из 4 групп по 6 игроков. В первом случае необходимо провести всего 6 игр в каждой группе, во втором – 15. Ввиду того, что каждая игра состоит из 3, 5 или 7 партий, общее время проведения турнира необходимо увеличить в соответствующее число раз. Исходя из приведенного выше концептуального описания возможных вариантов жеребьевки, было принято решение о целесообразности построения алгоритма и его програм- мной реализации, опираясь на эвристику змейки.
, где n – число игроков в группе. Например, при общем числе игроков N = 24 наиболее типичной является турнирная таблица, состоящая из 6 групп по 4 игрока в каждой группе или из 4 групп по 6 игроков. В первом случае необходимо провести всего 6 игр в каждой группе, во втором – 15. Ввиду того, что каждая игра состоит из 3, 5 или 7 партий, общее время проведения турнира необходимо увеличить в соответствующее число раз. Исходя из приведенного выше концептуального описания возможных вариантов жеребьевки, было принято решение о целесообразности построения алгоритма и его програм- мной реализации, опираясь на эвристику змейки.
