Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Методика и программа для статистического исследования алгоритмов разрезания графов
Аннотация:
Abstract:
| Авторы: Павленко А.В. () - , Пикулин В.В. (pvv@pgta.ru) - Пензенская государственная технологическая академия, кандидат технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10973 |
Версия для печати Выпуск в формате PDF (1.53Мб) |
Проектирование и модернизация информационных систем (ИС) в настоящее время выполняется преимущественно с использованием средств автоматизации (CASE-средств), которые позволяют выполнять процессы структурного анализа и синтеза в диалоговом режиме. Однако проектирование структуры ИС в таком режиме является достаточно трудоемким процессом, поэтому рассматривается небольшое количество вариантов проектных решений, что снижает эффективность результатов проектирования ИС. Таким образом, актуальными являются задачи автоматического синтеза, анализа и выбора вариантов проектных решений по структуре ИС. Для формирования вариантов структуры ИС предлагается использовать модель в виде взвешенного (по дугам) ориентированного мультиграфа и ряд алгоритмов выделения подграфов, обладающих заданными свойствами. Такой метод синтеза вариантов структуры ИС позволяет структурировать и объединять сильно связанные информационными потоками процессы в модели ИС. Основные процедуры таких алгоритмов: выбор начальной вершины для очередного подграфа, выбор одной или нескольких вершин для включения в подграф, проверка условий окончания процедуры формирования очередного подграфа. Правила выбора формулируются таким образом, чтобы обеспечить формирование сильно связанных подграфов (табл. 1), однако эвристические правила не гарантируют формирования оптимального (по заданным показателям) результата. Разработка математических моделей для оценки качества эвристических алгоритмов (по показателям назначения) представляет значительную сложность, поэтому целесообразно использовать методы статистических исследований. Авторами разработана соответствующая методика и инструментальное программное средство «GraphTool». Методика исследования включает в себя определение процедуры и показателей оценки качества решений. Процедура исследования включает следующие операции: 1) задание характеристик генерируемых ориентированных взвешенных мультиграфов (условий задач); 2) выбор алгоритмов для решения задачи разрезания; 3) генерация графа с заданными характеристиками; 4) решение задачи разрезания сгенерированного графа по всем выбранным алгоритмам; 5) вычисление значений показателей, характеризующих результат решения для каждого из алгоритмов, и сохранение в базе данных; 6) переход к п. 3 (генерация нового графа) заданное количество раз; 7) сравнение результатов решения задач, полученных по различным алгоритмам. Для оценивания качества результатов решения задач использованы следующие показатели: - отношение суммарного веса внутренних дуг к суммарному весу внешних дуг для каждого подграфа, - отношение количества внутренних дуг к количеству внешних дуг для каждого подграфа, - количество подграфов, - среднее число вершин в подграфе, - среднее число дуг в подграфе, - интегральный показатель эффективности. В качестве интегрального показателя используется аддитивный показатель, включающий частные показатели с весами, устанавливаемыми экспертным путем: Для корректного построения интегрального показателя частные показатели должны находиться в одинаковом диапазоне и иметь одинаковую размерность; для этого используются относительные значения. В данной работе использованы следующие частные показатели: Rверш – отношение суммарного веса внутренних дуг к суммарному весу внешних дуг для каждого подграфа; Rдуг – отношение количества внутренних дуг к количеству внешних дуг для каждого подграфа; RВП – отношение среднего количества вершин в подграфе к заданному максимальному количеству вершин в подграфе; Результаты экспериментов, приведенные в данной работе, получены при следующих значениях весовых коэффициентов: kверш=60; kдуг=30; kВП=10. Значения весовым коэффициентам были присвоены исходя из значимости (в данной предметной области) показателей, к которым они относятся. В разработанном программном средстве исследования алгоритмов введен набор характеристик, определяющих алгоритм (табл. 1). Таблица 1 Характеристики алгоритмов
Характеристиками генерируемых графов (условиями составляемых задач) являются количество вершин, количество дуг, максимальное количество вершин в одном подграфе, минимальное и максимальное значение весов дуг в графе, минимальное и максимальное значение меток вершин в графе. Схемы графов генерируются автоматически случайным образом; при этом необходимо соблюдение следующих условий: - соотношение количества дуг и количества вершин должно соответствовать связному графу; - количество связей между вершинами должно соответствовать количеству информационных потоков между процессами в рассматриваемой предметной области; - распределение значений весов дуг, генерируемых датчиком случайных чисел, должно соответствовать требуемому закону распределения значений выбранного показателя в данной предметной области. В процессе решения задач программа «GraphTool» вычисляет и сохраняет в базе данных значения показателей эффективности решения. Затем вычисляются значения интегрального показателя эффективности для каждого алгоритма, и выполняется сравнительный статистический анализ эффективности применения алгоритмов. Программное средство «GraphTool» позволяет просмотреть результаты решения задач и показатели эффективности в табличном виде и в виде круговых диаграмм и графиков, например: - частота формирования алгоритмом самого эффективного решения; - среднее значение одного из показателей по каждому алгоритму; - график изменений одного из показателей для всех задач по каждому алгоритму. Для исследования были использованы алгоритмы, характеристики которых приведены в таблице 2. Выполнено исследование шести вариантов алгоритмов, отличающихся набором характеристик на тестовых наборах с указанными в таблице 3 условиями задач. Таблица 2 Алгоритмы решения задач разрезания графов
В таблице 4 приведены результаты исследований на выборке объемом 200 задач для каждого алгоритма. Таблица 3 Значения условий задач
Таблица 4 Результаты испытаний эффективности алгоритмов
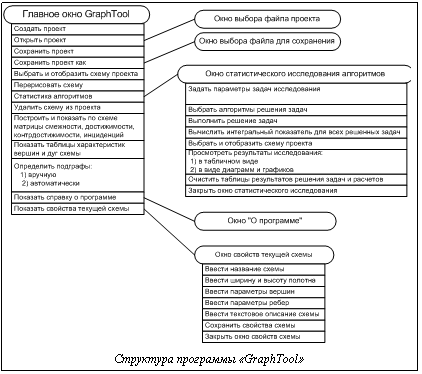
Программа «GraphTool» реализована в среде программирования Delphi; структура программы приведена на рисунке (см. выше), где овалы обозначают объекты для диалога, а прямоугольники – основные процедуры. Разработанные методика и программа позволяют проводить исследование различных алгоритмов разрезания рассмотренных графовых моделей ИС с целью выбора предпочтительных по критериям качества решения. Такие алгоритмы и разработанные процедуры разрезания ориентированных мультиграфов могут использоваться для развития возможностей современных CASE-средств (для анализа и синтеза ИС). Разработанная программа может быть дополнена другими процедурами решения задачи разрезания, что позволит расширить возможности для исследований. Проведенные на вышеопределенном наборе алгоритмов исследования позволили установить, что наиболее эффективными по указанным показателям являются алгоритмы №1 (набор характеристик: Р11 Р21 Р31 Р41) и №6 (набор характеристик: Р11 Р21 Р31 Р42). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?id=413&page=article |
Версия для печати Выпуск в формате PDF (1.53Мб) |
| Статья опубликована в выпуске журнала № 1 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Компьютер - хранитель домашнего очага
- Построение маршрута с максимальной пропускной способностью методом последовательного улучшения оценок
- Зарубежные базы данных по программным средствам вычислительной техники
- Потоковый анализ программ, управляемый знаниями
Назад, к списку статей



 Особенностями данной методики является то, что она позволяет формально определить новую структуру системы при минимальном участии пользователя, что, в свою очередь, позволит работать с большим количеством объектов предметной области одновременно. Задача автоматического формирования вариантов ИС сводится к задаче разрезания взвешенного ориентированного графа, который может соответствовать различным уровням иерархии ИС. Задача разрезания может решаться с помощью различных алгоритмов, из которых практически используются эвристические последовательные, имеющие невысокую временную сложность и формирующие приемлемые для практики результаты.
Особенностями данной методики является то, что она позволяет формально определить новую структуру системы при минимальном участии пользователя, что, в свою очередь, позволит работать с большим количеством объектов предметной области одновременно. Задача автоматического формирования вариантов ИС сводится к задаче разрезания взвешенного ориентированного графа, который может соответствовать различным уровням иерархии ИС. Задача разрезания может решаться с помощью различных алгоритмов, из которых практически используются эвристические последовательные, имеющие невысокую временную сложность и формирующие приемлемые для практики результаты. , где ki – весовые коэффициенты, k>0,
, где ki – весовые коэффициенты, k>0,  ; Ri – нормированный частный показатель.
; Ri – нормированный частный показатель.