Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритмы автоматизированной системы управления испытанием оборудования на надежность
Аннотация:Повышения экономической эффективности системы испытания оборудования на надежность можно добиться, сократив время испытаний или уменьшив количество испытуемых образцов. При сокращении времени испытаний возрастает степень цензурирования выборки, а при уменьшении количества образцов уменьшается объем выборки наработок оборудования. Сокращать параметры испытаний можно только в случае, если методы обработки информации обеспечивают достоверность рассчитанных показателей надежности. В результате испытаний формируются малые цензурированные выборки наработок оборудования на отказ. Расчет показателей надежности по таким выборкам выполняется методом максимального правдоподобия. В статье представлены экспериментальные исследования точности оценки максимального правдоподобия параметра экспоненциального закона распределения по малым, однократно цензурированным справа выборкам. Исследования выполнялись моделированием на компьютере цензурированных выборок, подобных выборкам, формирующимся при испытаниях оборудования на надежность. Эти экспериментальные данные показывают, что большинство оценок максимального правдоподобия, полученных по малым, однократно цензурированным справа выборкам, имеют значительные отклонения от истинных значений. В работе построены регрессионные модели, устанавливающие зависимость между отклонением оценки максимального правдоподобия от истинного значения и параметрами, характеризующими структуру выборки. Они позволяют рассчитать и ввести поправки к оценкам максимального правдоподобия. Были проведены экспериментальные исследования результатов их использования. Точность оценок максимального правдоподобия после применения разработанных моделей и введения поправки к оценкам максимального правдоподобия значительно возрастает. Разработано ПО для применения регрессионных моделей на практике.
Abstract:Economic efficiency of equipment reliability test system can be improved by running time reduction or decrease in the amount of specimens. When running time reduces, sample trimming rating increases. Decrease in the amount of specimens leads to decrease in the sample number of equipment running. Evaluation test specifications may be reduced only if information processing methods ensure the validity of the calculated reliability characteristics. The result of test operations is forming small censored samples of mean-time-between-equipment failures. Reliability measurement using such samples is made by the maximum likelihood method. The article presents experimental studies of estimating precision of maximum a likelihood parameter of the exponential distribution law on small singly right-censored samples. In their studies the authors used computer simulating of censored samples, which are similar to the samples formed in equipment reliability testing. These experimental data show that the majority of maximum likelihood estimates obtained using small singly right-censored samples have significant deviations from ideal values. The work includes regression models that set a relation between a deviation of maximum likelihood estimate from ideal value and the parameters characterizing the sample structure. They allow calculating and putting amendments to maximum likelihood estimates. The paper also includes experimental studies of its usage results. After applying developed models and putting amendments to maximum likelihood estimates the accuracy of maximum likelihood estimates increases. There also is a developed software to apply regression models in practice.
| Авторы: Русин А.Ю. (alrus@tvcom) - Тверской государственный технический университет (доцент), Тверь, Россия, кандидат технических наук, Абдулхамед М. (alrus@tvcom) - Тверской государственный технический университет (аспирант), Тверь, Россия, Барышев Я.В. (alrus@tvcom) - Тверской государственный технический университет (аспирант), Тверь, Россия | |
| Ключевые слова: программное обеспечение, метод максимального правдоподобия, цензурированные выборки, надежность, испытания оборудования, обработка информации, компьютерное моделирование |
|
| Keywords: the software, maximum likelihood method, censored samples, reliability, equipment test, information processing, computer modeling |
|
| Количество просмотров: 13845 |
Версия для печати Выпуск в формате PDF (7.11Мб) Скачать обложку в формате PDF (0.37Мб) |
Современная АСУ производственными процессами объединяет много различных подсистем, каждая из которых решает задачи автоматизации локальных процессов [1]. Одной из таких подсистем является АСУ испытанием оборудования на надежность. Разработанная авторами статьи АСУ испытанием оборудования представляет собой ПО, написанное на СУБД Visual FoxPro, для хранения, отображения и обработки информации о наработках на отказ, полученных при проведении испытаний. Данная АСУ испытанием оборудования предназначена не только для хранения полученной информации и отображения ее в наиболее удобном виде, но и для расчетов достоверных показателей надежности испытуемого оборудования. Структура системы приведена на рисунке 1. Развитие этой АСУ идет в двух направлениях: совершенствование структуры БД, интерфейса программы и выходных печатных форм, а также разработка новых и совершенствование существующих методов расчета показателей надежности испытуемого оборудования. ПО АСУ испытанием оборудования позволяет реализовать несколько существующих планов испытаний, описанных в [2, 3]. В результате их применения формируются цензурированные справа выборки наработок на отказ. Основным методом при оценке параметров законов распределения по цензурированным выборкам является метод максимального правдоподобия [4, 5]. В работе [6] разработана методика, позволяющая повысить достоверность оценок метода максимального правдоподобия. Она использована в АСУ испытанием оборудования для совершенствования алгоритмов расчета параметров надежности при испытаниях оборудования по плану [N, U, T], который приведен в стандарте ГОСТ 27.410–87. Со- гласно этому плану, одновременно испытывают N объектов, отказавшие во время испытаний объекты не восстанавливают и не заменяют, испытания прекращают по окончании времени наблюдений или по достижении наработки Т для каждого неотказавшего объекта [7]. При проведении испытаний по плану [N, U, T] формируются однократно цензурированные выборки наработок на отказ. Предложенный в данной работе алгоритм, позволяющий повысить достоверность оценок показателей надежности параметрическими методами и реализованный в АСУ испытанием оборудования, заключается в следующем. 1. Выполняется расчет оценок максимального правдоподобия (ОМП) для выбранного закона распределения по сформированным в результате испытаний однократно цензурированным выборкам наработок на отказ оборудования. 2. Рассчитываются параметры выборки, характеризующие ее структуру. 3. Осуществляется расчет поправки к ОМП по регрессионным моделям, устанавливающим зависимость между отклонением ОМП и параметрами выборки. 4. Вводится поправка к ОМП. Для получения регрессионных моделей и апробации предложенного алгоритма при параметрической оценке показателей надежности оборудования, отказы которого имеют экспоненциальное распределение, была разработана программа моделирования на языке Visual FoxPro. Алгоритм моделирования заключается в следующем. 1. Генерируется случайная величина t, распределенная по экспоненциальному закону распределения и рассчитываемая по формуле 2. Полученные случайные величины сравниваются с заданным временем проведения испытаний T. Если t < T, к моделируемой выборке добавляется случайная величина t, соответствующая наработке до отказа. Если t > T, к моделируемой выборке добавляется случайная величина T, соответствующая наработке до цензурирования. 3. Процесс моделирования продолжается до тех пор, пока число полученных случайных величин не станет равным заданному числу членов выборки N (объему выборки). В исследованиях ставилась задача получения универсальных уравнений, которые можно применять для оборудования с разными значениями средних наработок до отказа. Поэтому параметр l исследуемого закона распределения рассчитывался для каждой генерируемой выборки с использованием случайного числа, равномерно распределенного на интервале [0, 1] с помощью функции RAND() – функции генерации случайного числа, равномерно распределенного на интервале [0, 1], и языка программирования FoxPro. Чтобы избежать повторения последовательностей псевдослучайных чисел, возникающего из-за высокого быстродействия современных процессоров, перед формированием каждой выборки генерировалось случайное число на основе системного времени. Для этого использовалась функция RAND() с отрицательным аргументом RAND(–1). Получение достаточной разницы в системном времени при генерации выборок осуществлялось с помощью задержки времени до 30 миллисекунд перед каждым циклом формирования однократно цензурированной выборки. 4. Рассчитываются параметры выборки, характеризующие ее структуру. Для описания структуры сформированной выборки случайных величин в работе использовались пять стандартных параметров [9]: X1 – степень цензурирования, X2 – коэффициент вариации, X3 – коэффициент вариации полных случайных величин, X4 – эмпирический коэффициент асимметрии, X5 – коэффициент эксцесса. Еще пять параметров представляют собой математические выражения, составленные из стандартных характеристик выборки: X6 – отношение математического ожидания полных случайных величин к математическому ожиданию всех членов выборки, X7 – отношение математического ожидания цензурированных случайных величин к математическому ожиданию всех членов выборки, X8 – относительное отклонение матожидания от середины вариационного размаха, X9 – отношение медианы к математическому ожиданию, X10 – отношение моды к математическому ожиданию. Все параметры измеряются в относительных единицах и не зависят от абсолютных значений случайных величин. Это сделано для того, чтобы полученные уравнения можно было применять к оборудованию со средними наработками на отказ разной величины. 5. Рассчитывается ОМП экспоненциального распределения. 6. Вычисляется зависимый параметр регрессионных моделей – относительное отклонение ОМП от истинного значения по формуле На ЭВМ моделировались однократно цензурированные справа выборки случайных величин объемом N=5, 10, 15, 20. Генерирование выборок выполнялось при следующих ограничениях: 6£N<10, q ³ 0,5; 10 £ N < 20, q ³ 0,3; 20 £ N £ 50, q ³ 0,2, где q – степень цензурирования выборки. Количество сформированных выборок V для каждого значения N равно 3 000. В результате компьютерного моделирования построены линейные регрессионные математические модели, устанавливающие связь между отклонением ОМП от истинного значения и параметрами, характеризующими структуру выборки. Для каждого объема выборки N построено свое уравнение регрессии [10] вида
Полученные уравнения регрессии позволяют повысить точность ОМП введением к ней поправки
где lКОН – конечная оценка параметра распределения. Для оценки эффективности предложенного алгоритма и построенных регрессионных моделей был проведен новый эксперимент компьютерного моделирования. Выборки генерировались заново. Для каждой сгенерированной выборки были рассчитаны ОМП lОМП параметра экспоненциального распределения, поправка к ОМП по уравнениям регрессии (2), конечная оценка параметра распределения lКОН по выражению (3), относительные отклонения sнач и sкон полученных оценок от истинного значения параметра экспоненциального распределения, которое использовалось при генерации выборки. По результатам исследований уравнений регрессии построены гистограммы относитель- ных отклонений оценок от истинного значения (рис. 2–5). Графики, приведенные на этих рисунках, пока- зывают, что точность ОМП после применения разработанных моделей и введения поправки возрастает. Наибольший эффект от введения поправок ОМП экспоненциального распределения достига- ется при числе членов выборки N=5. В целом можно сделать вывод о том, что введение поправок позволяет повысить точность ОМП в зависимости от объема выборки в 1,2–2 раза. Применение разработанной АСУ испытанием оборудования позволит сократить затраты на проведение испытаний путем сокращения времени их проведения или количества испытуемых образцов при сохранении достоверности полученных результатов. Литература 1. Ицкович Э.Л. Методы комплексной автоматизации производства предприятий технологических отраслей. М.: КРАСАНД, 2013. 232 с. 2. Дорохов А.Н., Керножицкий В.А., Миронов А.Н., Шестопалова О.Л. Обеспечение надежности сложных технических систем. СПб: Лань, 2011. 348 с. 3. Шишко В.Б., Чиченев Н.А. Надежность технологического оборудования. М.: Изд-во МИСиС, 2012. 190 с. 4. Лемешко Б.Ю., Лемешко С.Б., Постовалов С.Н., Чимитова Е.В. Статистический анализ данных, моделирование и исследование вероятностных закономерностей. Компьютер- ный подход: монография. Новосибирск: Изд-во НГТУ, 2011. 888 с. 5. Рассел Д., Колин Р. Метод максимального правдоподобия. М.: VSD, 2013. 111 с. 6. Русин А.Ю., Абдулхамед М. Обработка информации в системе испытаний промышленного оборудования на надежность // Технологии техносферной безопасности. 2014. № 4 (56). URL: http://ipb.mos.ru/ttb (дата обращения: 20.03.2016). 7. Труханов В.М. Надежность технических систем. М.: Машиностроение-1, 2008. 584 с. 8. Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: ЛИБРОКОМ, 2014. 352 с. 9. Ивановский Р.И. Теория вероятностей и математическая статистика: основы, прикладные аспекты с примерами и задачами в среде Mathcad. СПб: БХВ-Петербург, 2008. 528 с. 10. Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных. М.: Юрайт, 2011. 399 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=4143&page=article |
Версия для печати Выпуск в формате PDF (7.11Мб) Скачать обложку в формате PDF (0.37Мб) |
| Статья опубликована в выпуске журнала № 2 за 2016 год. [ на стр. 23-26 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Проблемы управления конфигурациями в процессе разработки программного обеспечения встроенных систем
- Метод испытания радиолокационных станций с использованием беспилотного летательного аппарата и бортового оборудования
- Взаимодействие конкурирующих интеллектуальных агентов в распределенных мультиагентных системах
- Программный комплекс для разметки и унифицированного описания лица индивида по фотоизображению
- Операционная система реального времени Багет 3.0
Назад, к списку статей




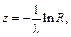 где R – случайная величина, равномерно распределенная на интервале (0, 1) [8].
где R – случайная величина, равномерно распределенная на интервале (0, 1) [8]. где l – истинное значение параметра экспоненциального распределения; lОМП – ОМП экспоненциального распределения.
где l – истинное значение параметра экспоненциального распределения; lОМП – ОМП экспоненциального распределения. . (2)
. (2) по формуле
по формуле , (3)
, (3)

