Математическое моделирование температурных полей в изделиях играет важнейшую роль в большинстве технологических процессов различных отраслей промышленности. Это процессы отжига стекла, обжига силикатного кирпича, закалки металлических изделий и другие, связанные с выбором режимов термообработки производимых изделий [1]. Геометрическая форма изделий может быть различной: плоской, цилиндрической, в виде параллелепипеда или более сложной. Одним из подходов при решении температурных задач в этом случае является приведение сложного изделия к плоской форме за счет введения характерного или эффективного размера [2]. В качестве такого размера для полого цилиндрического тела может выступать толщина стенки, параллелепипеда – наименьший из размеров (для ленты – ее толщина) и т.д. Это позволяет при получении температурного поля решать дифференциальное уравнение теплопроводности для одномерного случая:
 (1)
(1)
где t(x, t) – значение температуры в координате по толщине x в момент времени t (°C); a – коэффициент температуропроводности материала изделия (м2/с) [3].
Большую роль для точного моделирования температурных распределений в изделиях играет корректный учет начальных и граничных условий, которые в большинстве стадий технологических процессов термообработки имеют сложный характер. Так, начальные условия обычно неравномерны, граничные условия соответствуют несимметричному конвективно-радиационному теплообмену поверхностей изделия с окружающей средой и ограждающими поверхностями (нагревательными элементами) технологического оборудования [4, 5]. В этом случае наиболее удобны численные конечно-разностные методы, при использовании которых частные производные в уравнении (1) по времени и координате заменяются на их численные аналоги соответственно [ti+1(r) – ti(r)]/Dt и [ti(r–1) – – 2ti(r) + ti(r+1)]/(D )2.
)2.
Здесь  – номер временной точки расчета;
– номер временной точки расчета;  – номер точки по толщине
– номер точки по толщине  D
D = =
= =  /N
/N – толщина слоя; Dt – шаг по времени [3].
– толщина слоя; Dt – шаг по времени [3].
Тогда формулы для расчета температурного распределения во внутренних точках плоского тела будут выглядеть следующим образом:
 (2)
(2)
При расчете конвективного теплообмена необходимо приравнять тепловые потоки на поверхности, например r=0, в соответствии с законами Фурье: q(0, t)=–l׶t(0, t)/¶x и Ньютона: q(0, t) = = a1[t(0, t) – tc1(t)] [6]. Тогда градиент ¶t(0, t)/¶x= = a1[tc1(t) – t(0, t)]/l, а вторая производная на поверхности r=0:


и по аналогии для поверхности r=N:
 (3)
(3)
где a1, a2 – коэффициенты конвективной теплоотдачи для нижней и верхней поверхностей изделия (Вт/(м2град)); tc1(t), tc2(t) – температуры среды под и над пластиной (°C); l – коэффициент теплопроводности материала (Вт/(м·град)).
При расчете радиационного теплообмена с учетом закона Стефана–Больцмана по аналогии с (3) и (4) вторые производные на поверхностях r=0 и r=N находятся по выражениям:
 (4)
(4)
где es1, es2 – приведенные степени черноты нижней и верхней ограждающих поверхностей технологического оборудования; s = 5,67·10-12 (Вт/(м2K4)) – постоянная Стефана–Больцмана; TH1(t), TH2(t) – температуры ограждающих поверхностей под и над изделием (K).
C учетом передачи тепла точкам поверхностей изделия от внутренних соседних точек за счет теплопроводности получим окончательные выражения для расчета температур поверхностей плоского тела в виде:
 (5)
(5)
Для проверки модели температурного поля (2)–(5) был рассмотрен cлучай конвективно-радиационного охлаждения стеклянной пластины, приведенный в [3, 7]. При расчете использованы cледующие значения параметров: a=0,2 (см2/мин.); l=0,00838 (Вт/(см∙град.));  = 0,6 (см); εs1=εs2=0,91; N=6;
= 0,6 (см); εs1=εs2=0,91; N=6;  =0,1 (см); a1=a2=0,001256 (Вт/см2град.); t0(r)=707 (°C); tс1=tс2=27(°C); tн1=tн2=27 (°C); Dt=0,5 (с). Результаты расчета, приведенные в таблице 1, хорошо согласуются с источниками.
=0,1 (см); a1=a2=0,001256 (Вт/см2град.); t0(r)=707 (°C); tс1=tс2=27(°C); tн1=tн2=27 (°C); Dt=0,5 (с). Результаты расчета, приведенные в таблице 1, хорошо согласуются с источниками.
Таблица 1
Распределение температур в неограниченной пластине при симметричном конвективно-радиационном охлаждении
Table 1
Temperature distribution in a unconfined plate at symmetrical convective-radiant cooling
|
Время расчета t, с
|
0
|
6
|
10
|
20
|
30
|
60
|
120
|
¥
|
|
Поверхность t(0)
|
707,0
|
624,7
|
605,1
|
565,5
|
531,4
|
450,6
|
344,8
|
27,0
|
|
Центр t(3)
|
707,0
|
694,5
|
674,4
|
625,1
|
582,7
|
485,8
|
365,1
|
27,0
|
Решение поставленной задачи также может быть получено с помощью стандартной функции pdepe среды программирования Matlab [8, 9]. Рассмотрим характерные особенности разработки такой программы.
Для использования pdepe необходимо корректное задание трех функций: типа дифференциального уравнения pdedif, начальных условий pdebeg и граничных условий pdebound. Решаемое дифференциальное уравнение в pdepe описывается следующим образом:
 (6)
(6)
где m=0 – константа формы, равная 0, 1, 2 соответственно для пластины, цилиндра, шара; c(x, t, t, ¶t/¶x)=1/a – коэффициент при ¶t/¶t в формуле (1); f(x, t, t, ¶t/¶x)= ¶t/¶x; s(x, t, t, ¶t/¶x)=0 – отсутствующий член с источником излучения.
Граничные условия в pdepe описываются выражением для x=0 на нижней и x= на верхней поверхностях плоского изделия:
на верхней поверхностях плоского изделия:
p(x, t, t)+ q(x, t)× f(x, t, t, ¶t/¶x)=0, (7)
где q(0, t)= q( , t)=1 – коэффициенты при градиентах ¶t(0, t)/¶x и ¶t(
, t)=1 – коэффициенты при градиентах ¶t(0, t)/¶x и ¶t( t)/¶x;
t)/¶x;
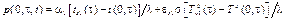 ;
;  – формулы для градиентов на поверхностях пластины при несимметричном конвективно-радиационном теплообмене.
– формулы для градиентов на поверхностях пластины при несимметричном конвективно-радиационном теплообмене.
Поэтому вышеуказанные функции типа дифференциального уравнения, начальных и граничных условий для рассмотренного примера выглядят следующим образом:
function [c,f,s]=pdedif(x,tau,t,dtdx)
global a
c = 1/a;
f = dtdx;
s = 0;
function t0=pdebeg(x)
t0=707;
function [pl,ql,pr,qr]=pdebound(xl,tl,xr,tr,tau)
global alfa1 alfa2 es1 es2 sig Kel lambd
tc1=27; tc2=27;
tn1=27; tn2=27;
pl=alfa1/lambd*(tc1-tl)+es1*sig/lambd*((tn1+Kel)^4-(tl+Kel)^4);
ql = 1;
pr=-alfa2/lambd*(tc2-tr)-es2*sig/lambd*((tn2+Kel)^4-(tr+Kel)^4);
qr = 1;
Приведем текст основной программы с использованием функции pdepe:
clear
close all
clc
global a alfa1 alfa2 es1 es2 sig Kel lambd
m = 0; sig=5.67e-12; Kel=273.15; es1=0.91; es2=es1;
l=0.6; N=15; a=0.2; Ntau=241; lambd=0.00838;
tau_fin=2; alfa1=0.001256; alfa2=0.001256;
x = linspace(0,l,N);
tau = linspace(0,tau_fin,Ntau);
options=odeset('RelTol',1e-4);
sol = pdepe(m,@pdedif,@pdebeg,@pdebound,x,tau,options);
t = sol(:,:,1)
surf(x,tau,t)
title(strcat('Температурное поле для числа точек по координате N=',num2str(N)))
xlabel('Координата x, см')
ylabel('Время \tau, мин')
 Полученная поверхность рассчитанного температурного распределения приведена на рисунке.
Полученная поверхность рассчитанного температурного распределения приведена на рисунке.
Результаты расчета температурного поля в пластине в среде Matlab приведены в таблице 2. Разница с результатами, полученными с помощью конечно-разностных соотношений (2)–(5), не превышает 1°C.
Таблица 2
Распределение температур в неограниченной пластине при симметричном конвективно-радиационном охлаждении, полученное в среде Matlab
Table 2
Temperature distribution in a unconfined plate at symmetrical convective-radiant cooling in Matlab
|
Время расчета t, с
|
0
|
6
|
10
|
20
|
30
|
60
|
120
|
¥
|
|
Поверхность t(0)
|
707,0
|
624,7
|
605,2
|
565,7
|
531,8
|
451,1
|
345,4
|
27,0
|
|
Центр t(3)
|
707,0
|
693,8
|
673,9
|
625,0
|
582,9
|
486,3
|
365,7
|
27,0
|
Предложенные модели температурного поля в изделиях плоской формы при их конвективно-радиационном теплообмене с окружающей средой и ограждающими поверхностями можно использовать для идентификации условий теплообмена и оптимизации режимов их термообработки в различных технологических процессах [10]. Идентификация позволяет найти параметры конвективного (коэффициенты теплоотдачи) и радиационного (приведенные степени черноты) теплообмена, обеспечивающие совпадение рассчитанных по модели температур поверхностей изделия с их экспериментальными значениями с некоторой точностью. Оптимизация направлена на сокращение длительности технологического процесса или энергетических затрат на процесс термообработки изделия.
Наличие в Matlab наряду с pdepe функции fmincon, эффективно решающей задачи нелинейной оптимизации функции нескольких переменных с ограничениями типа неравенств и равенств, позволяет говорить о перспективности использования этой среды программирования для последующего решения задач идентификации и оптимизации.
Литература
1. Рубанов В.Г. Автоматизация и управление объектами промышленности строительных материалов // Строительные материалы. 1996. № 2. С. 18–19.
2. Мазурин О.В., Белоусов Ю.Л. Отжиг и закалка стекла: учеб. пособие. М.: Изд-во МИСИ и БТИСМ, 1984. 114 с.
3. Марголис Б.И. Моделирование полей температур и напряжений в стеклоизделиях: монография. Тверь: Изд-во ТвГТУ, 2001. 100 с.
4. Мазурин О.В., Лалыкин Н.В. Математическая модель процесса отжига листового стекла // Стекло и керамика. 1984. № 1. С. 13–15.
5. Марголис Б.И. Моделирование температурных полей в стеклоизделиях при их отжиге // Стекло и керамика. 2003. № 2. С. 3–5.
6. Лыков А.В. Теория теплопроводности: учеб. пособие. М.: Высш. школа, 1967. 599 с.
7. Gardon R. Calculation of temperature distributions in glass plates undergoing heat-treatment. J. Amer. Ceram. Soc., 1958, vol. 41, no. 6, pp. 200–209.
8. Лазарев Ю. Моделирование процессов и систем в MATLAB: учеб. курс. СПб: Питер, 2005. 512 с.
9. Дьяконов В.П. MATLAB 7.*/ R2006/ R2007: самоучитель. М.: ДМК Пресс, 2008. 768 с.
10. Марголис Б.И. Нахождение оптимального режима отжига стеклоизделий, обеспечивающего минимальные энергозатраты // Стекло и керамика. 2003. № 5. С. 12–13.

 (1)
(1) )2.
)2. – номер временной точки расчета;
– номер временной точки расчета;  – номер точки по толщине
– номер точки по толщине  D
D (2)
(2)

 (3)
(3) (4)
(4) (5)
(5) = 0,6 (см); εs1=εs2=0,91; N=6;
= 0,6 (см); εs1=εs2=0,91; N=6;  =0,1 (см); a1=a2=0,001256 (Вт/см2град.); t0(r)=707 (°C); tс1=tс2=27(°C); tн1=tн2=27 (°C); Dt=0,5 (с). Результаты расчета, приведенные в таблице 1, хорошо согласуются с источниками.
=0,1 (см); a1=a2=0,001256 (Вт/см2град.); t0(r)=707 (°C); tс1=tс2=27(°C); tн1=tн2=27 (°C); Dt=0,5 (с). Результаты расчета, приведенные в таблице 1, хорошо согласуются с источниками. (6)
(6) на верхней поверхностях плоского изделия:
на верхней поверхностях плоского изделия: t)/¶x;
t)/¶x;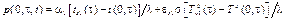 ;
;  – формулы для градиентов на поверхностях пластины при несимметричном конвективно-радиационном теплообмене.
– формулы для градиентов на поверхностях пластины при несимметричном конвективно-радиационном теплообмене.