Для решения разнообразных задач все чаще требуется мониторинг пространства. Под мониторингом в общем случае понимается систематическое наблюдение за каким-либо процессом с целью фиксации соответствия (или несоответствия) результатов этого процесса первоначальным предположениям. В данной работе рассмотрим мониторинг пространства, то есть поставим задачу оперативного обнаружения заранее заданного объекта на определенной территории (при его появлении). Среди таких задач наиболее интересной кажется задача обнаружения заранее заданных объектов на определенной ограниченной территории. Следует отметить, что целевой объект может иметь разную природу: являться не только физическим объектом (предметом), но и, например, сигналом. Такие задачи часто возникают при проведении метеорологических наблюдений [1], экологического мониторинга [2], мониторинга сложных технических систем [3] и т.д.
Задача делится на две составные части: задачу распознавания и задачу геометрического расположения. Действительно, необходимо, с одной стороны, определить механизм обнаружения и распознавания целевого объекта неким обнаружителем, а с другой, расположить этот обнаружитель таким образом, чтобы обнаружение осуществлялось наиболее качественно.
Первая задача носит частный характер для каждого конкретного случая и зависит от свойств и параметров объекта, обнаружителя и среды. Предлагается решать ее децентрализованной сетью мо- бильных сенсоров. Такой подход имеет ряд преимуществ, в числе которых масштабируемость, гибкость, оперативность развертывания и свертывания системы (следовательно, перебазирования), самоорганизационная устойчивость к изменению факторов воздействия внешней среды (вплоть до факторов, способствующих выходу из строя устройств), а также возможность создания за счет изменения количества сенсоров широкой области обзора. При этом под областью обзора понимается область, при появлении целевого объекта в которой обнаружение может быть осуществлено без изменения геометрического положения устройств (алгоритмов поиска цели). Сами устройства (сенсоры) будем также называть абонентами.
Задача оптимального геометрического расположения сенсоров сводится к поиску такого набора геометрических положений сенсоров, который гарантирует решение задачи мониторинга. Понятие эффективности решения на данном этапе не определяется, так как существенным образом зависит от специфики задачи, о которой будет упомянуто далее. Дело в том, что от начальных условий зависят сама постановка задачи, подходы к ее решению, а также понятия об эффективности решения задачи. В зависимости от геометрических параметров зоны мониторинга, а также количества сенсоров и геометрических параметров их зон принципиально выделяются два случая [4].
1. Существует такое множество точек в зоне мониторинга (за вычетом препятствий), что при размещении указанного (при задании начальных условий) числа сенсоров в них зона мониторинга полностью содержится в множестве, представляющем собой объединение зон видимости всех сенсоров. Иными словами, возможно покрытие зоны мониторинга указанным числом сенсоров с соответствующими характеристиками.
2. Зону мониторинга невозможно покрыть указанным (при задании начальных условий) числом зон видимости, соответствующих сенсорам, размещенным в зоне мониторинга (в любых точках, кроме препятствий).
Первый случай называется задачей покрытия, второй – задачей патрулирования. В данной статье рассматривается только первая задача.
Математическое описание задачи
Наиболее общая формулировка задачи покрытия такова:
- задана некая рабочая зона (зона мониторинга) – связная область пространства;
- даны N одинаковых устройств, каждому из которых соответствует своя зона покрытия (определяется аналогично для всех устройств);
- в рабочей зоне задано распределение конечного числа препятствий – связных множеств точек рабочей зоны, в которых устройства не могут находиться;
- каждое препятствие каким-либо образом (известным для каждой частной задачи) изменяет зону покрытия каждого устройства (в зависимости от взаимного расположения препятствия и устройства); после учета влияния всех препятствий образуется реальная зона видимости.
Требуется найти такие k£N наборов координат, что, если каждое устройство займет позицию, соответствующую одному из этих наборов (так, чтобы два устройства не использовали один набор координат), в рабочей зоне не будет точек, не входящих в реальную зону видимости какого-либо из устройств. При этом значение k должно быть минимальным из всех возможных.
Следует отметить следующий принципиальный момент. При подобной постановке задачи возможна ситуация, при которой препятствия будут изменять зону покрытия таким образом, что мониторинг в некоторых точках будет невозможен при любом взаимном расположении устройств. В таком случае будет сделан вывод о невозможном полном решении задачи с помощью сети таких устройств. Однако в какой-то мере задача может быть решена, поэтому при реальной постановке требуется ука- зать допустимые размеры слепых зон (зон, которые не могут входить в зону видимости ни одного из устройств независимо от расположения), при которых решение задачи считается допустимым.
Соответственно, математически представим задачу следующим образом.
· Дано связное ограниченное множество A, на котором задано K связных подмножеств Bi. При этом 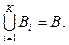 Считаем, что множества задаются на некоей евклидовой плоскости, а значит, можно вычислять расстояния между элементами этих множеств.
Считаем, что множества задаются на некоей евклидовой плоскости, а значит, можно вычислять расстояния между элементами этих множеств.
· Задан закон, ставящий в соответствие некоей точке рабочей зоны X=(x1, x2, x3) ограниченное связное множество C(X), которое содержит в себе точку X.
· Для каждого Bi задана функция fi, преобразующая C(X) в каждой точке X рабочей зоны. Таким образом, при заданном распределении Bi каждой точке X можно поставить в соответствие множество  .
.
Требуется найти k£N точек Xi, таких, что "iÎ{1, 2, ..., k}® XiÏB;  ; k®min.
; k®min.
Соответствие введенных обозначений реальным физическим характеристикам приводится в таблице 1.
Пример взаимного расположения рабочей зоны, препятствий и зон видимости показан на рисунке 1.
Дискретизация задачи и алгоритм ее решения
Сведем задачу к дискретной.
Рабочая зона A представляется в виде сетки (некоего аналога расчетной сетки [5, 6]) L={li} с шагом D.
Определяется сетка следующим образом:
- элементом сетки являются точки в рассматриваемом пространстве;
- для каждого элемента li на расстоянии D находится как минимум один элемент lj; если таких элементов несколько, расстояние между ними равно или 2D, или  соответственно; на евклидовой плоскости это соответствует некоей структуре, состоящей из квадратов, вершинами которых являются элементы L;
соответственно; на евклидовой плоскости это соответствует некоей структуре, состоящей из квадратов, вершинами которых являются элементы L;
- нет такой точки пространства A, в D-окрестности которой (на расстоянии, не превышающем D) не находился бы хотя бы один элемент сетки L.
С точки зрения физики шаг D должен быть пренебрежимо малым по отношению к характерным размерам задачи.
Итак, после перехода к описанию рабочей зоны в виде сетки начинается мышление в дискретных терминах. То есть, например, будем считать, что D(li) – дискретное множество, состоящее из элементов L, принадлежащих непрерывному множеству, соответствующему непрерывному D(li), описанному ранее.
Поскольку рабочая зона A ограничена и D – конечное число, можем считать, что задано конечное множество L=(l1, l2, ..., lM). Действительно, ограниченность множества  означает, что "xÎA $MÎN®
означает, что "xÎA $MÎN® где N – множество натуральных чисел; distr(x, y) – расстояние между элементами x и y. Соответственно, общее число элементов сетки не может превышать M 2 (при рассмотрении каждого элемента xÎA). Это очень грубая оценка, но она в полной мере подтверждает конечность множества L. Обозначим множество подмножеств L как S=(S1, S2, ..., Sp). Здесь Si=D(li) для всех liÎA\B. Таким образом, надо найти покрытие множества A – подмножество S ¢ÍS, такое, что
где N – множество натуральных чисел; distr(x, y) – расстояние между элементами x и y. Соответственно, общее число элементов сетки не может превышать M 2 (при рассмотрении каждого элемента xÎA). Это очень грубая оценка, но она в полной мере подтверждает конечность множества L. Обозначим множество подмножеств L как S=(S1, S2, ..., Sp). Здесь Si=D(li) для всех liÎA\B. Таким образом, надо найти покрытие множества A – подмножество S ¢ÍS, такое, что  .
.
Покрытие S¢ называется минимальным, если не существует покрытия S ²Í S ¢. Минимальных покрытий может быть несколько [7]. Покрытие S ¢ называется наименьшим, если для любого минимального покрытия S ² выполняется ½S ¢½£½S ²½, где ½X½ – мощность множества X [8]. Оптимально искать наименьшее покрытие S ¢ [9].
Лемма 1.
 Условие
Условие  является необходимым и достаточным условием того, что S ¢ – покрытие L.
является необходимым и достаточным условием того, что S ¢ – покрытие L.
Доказательство.
· Необходимость. Пусть S ¢ – покрытие L. Следовательно, выполняется условие  . Пред- положим, что
. Пред- положим, что  Значит,
Значит,  Однако, с другой стороны,
Однако, с другой стороны,  Значит,
Значит,  что может быть верным только в случае F=Æ. Что и требовалось доказать.
что может быть верным только в случае F=Æ. Что и требовалось доказать.
· Достаточность. 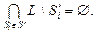 . Из этого следует, что
. Из этого следует, что  то есть S ¢ – покрытие L. Что и требовалось доказать.
то есть S ¢ – покрытие L. Что и требовалось доказать.
Лемма 2.
Покрытие S ¢ минимально тогда и только тогда, когда выполняется условие 
 , которое является необходимым и достаточным условием того, что покрытие S ¢ – минимальное покрытие L.
, которое является необходимым и достаточным условием того, что покрытие S ¢ – минимальное покрытие L.
Доказательство.
· Необходимость. Пусть S ¢ – минимальное покрытие L. Предположим, что  . Тогда рассмотрим S²= S¢\{S¢k}. Для этого множества выполняется
. Тогда рассмотрим S²= S¢\{S¢k}. Для этого множества выполняется  . Согласно лемме 1, это означает, что S² – покрытие L. Но S²Ì S¢, а значит, S ¢ не является минимальным покрытием L. Что и требовалось доказать.
. Согласно лемме 1, это означает, что S² – покрытие L. Но S²Ì S¢, а значит, S ¢ не является минимальным покрытием L. Что и требовалось доказать.
· Достаточность. Предположим, что условие  выполняется, но S ¢ не является минимальным покрытием L. Значит, $ S²Ì S ¢, при этом S² – покрытие L. Тогда, согласно лемме 1,
выполняется, но S ¢ не является минимальным покрытием L. Значит, $ S²Ì S ¢, при этом S² – покрытие L. Тогда, согласно лемме 1,  . Однако из условия
. Однако из условия  напрямую следует, что
напрямую следует, что  . Значит, S² не может быть покрытием L, то есть получаем противоречие. Что и требовалось доказать.
. Значит, S² не может быть покрытием L, то есть получаем противоречие. Что и требовалось доказать.
Метод построения полного нагруженного графа. Строим полный нагруженный граф G=(V, E, L(V), L(E)). В нем множеству вершин V={vi}, iÎ{1, 2, ..., p} взаимно однозначно сопоставляется множество L(V)={L(vi)}, где L(vi)=L\Si. Соответственно, число вершин равно мощности множества S. Каждая вершина  нагружена множеством L(vi).
нагружена множеством L(vi).
Множеству ребер E={eij}={(vi, vj)} сопоставляется множество L(E)={L(eij)}, где L(eij)= L(vi)ÇL(vj), i¹j. Множество всех ребер, инцидентных вершине vi, будем обозначать Ei. Множество всех вершин, инцидентных ребрам из множества Ei, будем обозначать V(Ei).
Лемма 3. Минимальное по мощности подмножество E¢iÍEi при выполнении условий L(vi)¹Æ,  определяет минимальное покрытие S ¢ множества L, однозначно соответствующее множе- ству V(E¢i)\{vi} вершин, если
определяет минимальное покрытие S ¢ множества L, однозначно соответствующее множе- ству V(E¢i)\{vi} вершин, если  , или множеству V(E¢i), если
, или множеству V(E¢i), если  .
.
Доказательство.
L(vi)¹Æ, следовательно, {Si} не является покрытием множества L.
Условие  в силу того, что, по определению, L(eij)= L(vi)ÇL(vj), i¹j, можно записать как
в силу того, что, по определению, L(eij)= L(vi)ÇL(vj), i¹j, можно записать как  Значит, согласно лемме 1, множество
Значит, согласно лемме 1, множество  соответствующее V(E¢i), определяет покрытие множества L.
соответствующее V(E¢i), определяет покрытие множества L.
Можно также утверждать, что при соблюдении условия  множество
множество  однозначно соответствующее V(E¢i)\{vi}, определяет покрытие множества L.
однозначно соответствующее V(E¢i)\{vi}, определяет покрытие множества L.
Установим теперь, являются ли эти покрытия минимальными. Исходя из предположения о том, что E¢iÍEi – минимальное по мощности подмножество, и рассматривая его, можно сделать вывод о возможности построения E¢i, удовлетворяющего условию леммы 2 (при рассмотрении отдельно множеств  и
и  с соблюдением соответствующих условий). Что и требовалось доказать.
с соблюдением соответствующих условий). Что и требовалось доказать.
Лемма 4. Минимальное по мощности подмножество E¢iÍEi при выполнении условий  "vÎV ®L(v)¹Æ,
"vÎV ®L(v)¹Æ,  определяет наименьшее покрытие S ¢, однозначно соответствующее множеству V(Ei)\{vi} вершин, если
определяет наименьшее покрытие S ¢, однозначно соответствующее множеству V(Ei)\{vi} вершин, если  , или множеству V(Ei), если
, или множеству V(Ei), если  .
.
Доказательство.
Поскольку "vÎV ®L(v)¹Æ, тривиального решения не существует.
E¢iÍEi выбирается таким образом, чтобы выполнялось условие  . Значит, используя лемму 3, можно сделать вывод о том, каким образом определяется минимальное покрытие. Однако, учитывая условие
. Значит, используя лемму 3, можно сделать вывод о том, каким образом определяется минимальное покрытие. Однако, учитывая условие  , можно сделать вывод о том, что данное покрытие также будет являться наименьшим. Что и требовалось доказать.
, можно сделать вывод о том, что данное покрытие также будет являться наименьшим. Что и требовалось доказать.
На основании всего вышесказанного, используя названные леммы, особенно лемму 4, можно выработать следующий алгоритм.
Алгоритм построения наименьшего покрытия множества L.
1. Имея множество L, задающее рабочую область, строим множество подмножеств S=(S1, S2, ..., Sp), где Si=D(li) для всех liÎA\B.
2. Ставим в соответствие этим множествам множество L(V(0))={L\Si}. Если один из его элементов – пустое множество, делаем вывод о том, что существует тривиальное решение, алгоритм закон- чен. Иначе – переход к шагу 3.
3. Строим полный нагруженный граф G(0)=(V(0), E(0), L(V(0)), L(E(0))). (О том, какие вершины и ребра какими множествами надо нагружать, уже говорилось.)
4. Проверка существования покрытия. Для произвольной вершины  определяется подмножество
определяется подмножество  . Если в результате получится непустое множество, делается вывод о том, что покрытия не существует, алгоритм закончен. В противном случае – переход к шагу 5.
. Если в результате получится непустое множество, делается вывод о том, что покрытия не существует, алгоритм закончен. В противном случае – переход к шагу 5.
5. k ¬ 0. Присвоение переменной k значения 0.
6. В полном нагруженном графе G(k) осуществляется поиск ребра  , для которого
, для которого  . Если
. Если  , осуществляется переход к шагу 8, иначе – к шагу 7.
, осуществляется переход к шагу 8, иначе – к шагу 7.
7. Строится полный нагруженный граф G(k+1)=(V(k+1), E(k+1), L(V(k+1)), L(E(k+1))) следующим образом:  ,
,  ,
,  ,
,  для всех
для всех  ,
,  , k ¬ k+1.
, k ¬ k+1.
Переход к шагу 6.
8. Начало построения наименьшего покрытия  .
.
9. Если k=0, осуществляется переход к шагу 12. В противном случае k¬k–1, переход к шагу 10.
10. В графе  определяется подмножество
определяется подмножество  .
.
11. Если в G(k) выполняется условие L(V)¹Æ, то  . Переход к шагу 9.
. Переход к шагу 9.
12. Множество  определяет наименьшее покрытие множества L.
определяет наименьшее покрытие множества L.
Конец алгоритма.
Лемма 5.
Трудоемкость алгоритма оценивается как O(p)=p3+p2.
Доказательство.
Вся вычислительная мощность реализуется при построении полного нагруженного графа. Число вершин графа совпадает с мощностью множества S и равняется p, как уже было определено ранее. Для p вершин графа имеем p действий по вычислению нагрузки в вершинах и  действий для вычисления нагрузки ребер полного графа. Такие вычисления выполняются (p–2) раза. Таким образом, грубая оценка O(p)=p3+p2.
действий для вычисления нагрузки ребер полного графа. Такие вычисления выполняются (p–2) раза. Таким образом, грубая оценка O(p)=p3+p2.
Величина p зависит от соотношения между размерами множества A\B и величиной D.
Программное моделирование
Для апробации разработанных алгоритмов была построена программная (компьютерная) модель, позволяющая провести ряд экспериментов и рассчитать основные показатели, свидетельствующие о работоспособности и эффективности представленного алгоритма.
На вход программы поступает обработанный участок карты какой-либо местности, соответствующий зоне мониторинга (рис. 2).
Также на вход программы подается число устройств, которым предполагается решить задачу. Зоны покрытия (видимости) каждого абонента считаются заранее заданными окружностями определенного радиуса. Препятствия не влияют на зоны видимости.
 Пример работы модели показан на рисунке 3, где найденные положения сенсоров обозначены зелеными точками. Для наглядности показано не только решение задачи покрытия для 12 абонентов, но и то, каким образом устройства, расположенные в обозначенных точках, покрывали бы своими зонами видимости весь участок пространства, соответствующий зоне мониторинга. Отметим достаточно большое число попарных пересечений зон видимости абонентов, характерных для зон видимости такой формы.
Пример работы модели показан на рисунке 3, где найденные положения сенсоров обозначены зелеными точками. Для наглядности показано не только решение задачи покрытия для 12 абонентов, но и то, каким образом устройства, расположенные в обозначенных точках, покрывали бы своими зонами видимости весь участок пространства, соответствующий зоне мониторинга. Отметим достаточно большое число попарных пересечений зон видимости абонентов, характерных для зон видимости такой формы.
Для проведения экспериментов использовались заранее обработанные участки карты Москвы. Поскольку здания имеют самые разные размеры и форму, для того чтобы охарактеризовать размер выбираемых участков, используется их отношение к радиусу зон видимости абонентов R.
В настоящей работе были рассмотрены 84 прямоугольных участка карт, линейные размеры которых 4R и 6R. Соответственно, площади рассматриваемых участков карты к площади зон видимости относятся как  . Таким образом, минимальное число устройств, для которых может быть решена задача покрытия при данных начальных условиях, равно 8.
. Таким образом, минимальное число устройств, для которых может быть решена задача покрытия при данных начальных условиях, равно 8.
По результатам моделирования были получены следующие результаты.
Программа успешно завершает свою работу (находит решение задачи) для 78 из 84 случайно выбранных карт, что составляет 93 %. Эта цифра постоянна для любого числа абонентов. Ситуации, при которых задача не может быть решена, возникают тогда, когда препятствия (в совокупности с границами зоны мониторинга) отсекают от выбранного участка карты связную область. В этом случае абонент никаким образом не может попасть туда и в некоторых случаях в силу этого не может осуществлять мониторинг в этой зоне. Также такая ситуация может возникнуть при слишком больших линейных размерах препятствий. Информация о количестве успешных решений задач покрытия для разного числа абонентов приведена в таблице 2.
Таблица 2
Зависимость решения задачи покрытия от числа абонентов
Table 2
The dependence of covering problem solution on the number of subscribers
|
Число абонентов
|
Задача покрытия, %
|
|
1
|
0,0
|
|
2
|
0,0
|
|
3
|
0,0
|
|
4
|
0,0
|
|
5
|
0,0
|
|
6
|
0,0
|
|
7
|
0,0
|
|
8
|
0,0
|
|
9
|
2,4
|
|
10
|
38,1
|
|
11
|
66,7
|
|
12
|
73,8
|
|
13
|
82,1
|
|
14
|
88,1
|
|
15
|
91,7
|
|
16
|
92,9
|
|
17
|
92,9
|
Из таблицы видно, что при использовании 16 абонентов задача успешно решается на максимально возможном проценте карт, соответственно, дальнейшее увеличение числа абонентов не приведет к изменению этого процента и будет бессмысленным.
 Зависимость процента карт, на которых успешно решается задача покрытия, от числа абонентов показана на графике (рис. 4), из которого следует, что уже для 13 абонентов задача покрытия решается более, чем в 80 % случаев, а для 15 – более, чем в 90 %. На основании этого графика можно делать вывод о вероятности успешного завершения случайной карты при выборе того или иного числа абонентов для решения задачи покрытия.
Зависимость процента карт, на которых успешно решается задача покрытия, от числа абонентов показана на графике (рис. 4), из которого следует, что уже для 13 абонентов задача покрытия решается более, чем в 80 % случаев, а для 15 – более, чем в 90 %. На основании этого графика можно делать вывод о вероятности успешного завершения случайной карты при выборе того или иного числа абонентов для решения задачи покрытия.
В целом результаты экспериментов показали работоспособность предложенных алгоритмов и подходов.
В заключение отметим, что в работе предложен и обоснован алгоритм, позволяющий решать задачу мониторинга пространства в частном случае. На его основе был разработан программный комплекс, позволяющий находить решение задачи мониторинга с помощью заданного числа мобильных сенсоров при известной карте пространства. Работоспособность алгоритма была подтверждена экспериментально. Общий подход, продемонстрированный в данной статье, позволяет применять разработанные методы для использования широкого спектра устройств в качестве субъектов мониторинга при решении соответствующих задач.
Разработанный программный комплекс имеет потенциал для применения при решении задач, связанных с мониторингом пространств децентрализованной сетью мобильных сенсоров. Данный комплекс может войти в число системы программ, позволяющей эффективно решать такие задачи.
Литература
1. Израэль Ю.А. Глобальная система наблюдений. Прогноз и оценка окружающей природной среды. Основы мониторинга // Метеорология и гидрология. 1974. № 7. С. 3–8.
2. Кондратьев А.Д., Королева Т.В., Пузанов А.В., Черницова О.В., Ефременков А.А., Шарапова А.В., Горбачев И.В., Двуреченская Е.Б. Совершенствование системы экологического мониторинга районов падения отделяющихся частей ракет-носителей // МНКО. 2012. № 6 (37). С. 483–486.
3. Кульба В.В., Сомов Д.С., Кочкаров А.А. Применение структурно-интегрированных индикаторов в мониторинге сложных технических систем // Изв. ЮФУ. Сер. Технич. науки. 2011. № 3 (116). С. 52–64.
4. Кочкаров А.А., Яцкин Д.В., Рахманов О.А. Особенно- сти решения задачи геометрического мониторинга // Изв. ЮФУ. Сер. Технич. науки. 2016. № 2 (175). С. 158–168.
5. Yap P. Grid-based path-finding. Advances in Artificial Intelligence, Springer, Berlin Heidelberg, 2002, pp. 44–55.
6. Thompson J.F., Warsi Z.A., Mastin C.V. Numerical grid generation, foundations and applications. North-Holland, 1985, 438 p.
7. Cheng M., Ruan L., and Wu W. Achieving minimum coverage breach under bandwidth constraints in wireless sensor networks. Proc. 24th Annual Joint Conf. of the IEEE Computer and Communications Societies, 2005, vol. 4, pp. 2638–2645.
8. Еремеев А.В., Заозерская Л.А., Колоколов А.А. Задача о покрытии множества: сложность, алгоритмы, экспериментальные исследования // Дискретный анализ и исследование операций. 2000. Т. 7. № 2. С. 22–46.
9. Батищев Д.Д., Неймарк Е.А., Старостин Н.В. Применение генетических алгоритмов к решению задач дискретной оптимизации. Н. Новгород: Изд-во НГУ, 2006.

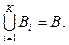 Считаем, что множества задаются на некоей евклидовой плоскости, а значит, можно вычислять расстояния между элементами этих множеств.
Считаем, что множества задаются на некоей евклидовой плоскости, а значит, можно вычислять расстояния между элементами этих множеств. .
. ; k®min.
; k®min. соответственно; на евклидовой плоскости это соответствует некоей структуре, состоящей из квадратов, вершинами которых являются элементы L;
соответственно; на евклидовой плоскости это соответствует некоей структуре, состоящей из квадратов, вершинами которых являются элементы L; означает, что "xÎA $MÎN®
означает, что "xÎA $MÎN® где N – множество натуральных чисел; distr(x, y) – расстояние между элементами x и y. Соответственно, общее число элементов сетки не может превышать M 2 (при рассмотрении каждого элемента xÎA). Это очень грубая оценка, но она в полной мере подтверждает конечность множества L. Обозначим множество подмножеств L как S=(S1, S2, ..., Sp). Здесь Si=D(li) для всех liÎA\B. Таким образом, надо найти покрытие множества A – подмножество S ¢ÍS, такое, что
где N – множество натуральных чисел; distr(x, y) – расстояние между элементами x и y. Соответственно, общее число элементов сетки не может превышать M 2 (при рассмотрении каждого элемента xÎA). Это очень грубая оценка, но она в полной мере подтверждает конечность множества L. Обозначим множество подмножеств L как S=(S1, S2, ..., Sp). Здесь Si=D(li) для всех liÎA\B. Таким образом, надо найти покрытие множества A – подмножество S ¢ÍS, такое, что  .
.
 является необходимым и достаточным условием того, что S ¢ – покрытие L.
является необходимым и достаточным условием того, что S ¢ – покрытие L. . Пред- положим, что
. Пред- положим, что  Значит,
Значит,  Однако, с другой стороны,
Однако, с другой стороны,  Значит,
Значит,  что может быть верным только в случае F=Æ. Что и требовалось доказать.
что может быть верным только в случае F=Æ. Что и требовалось доказать.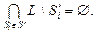 . Из этого следует, что
. Из этого следует, что  то есть S ¢ – покрытие L. Что и требовалось доказать.
то есть S ¢ – покрытие L. Что и требовалось доказать.
 , которое является необходимым и достаточным условием того, что покрытие S ¢ – минимальное покрытие L.
, которое является необходимым и достаточным условием того, что покрытие S ¢ – минимальное покрытие L. . Тогда рассмотрим S²= S¢\{S¢k}. Для этого множества выполняется
. Тогда рассмотрим S²= S¢\{S¢k}. Для этого множества выполняется  . Согласно лемме 1, это означает, что S² – покрытие L. Но S²Ì S¢, а значит, S ¢ не является минимальным покрытием L. Что и требовалось доказать.
. Согласно лемме 1, это означает, что S² – покрытие L. Но S²Ì S¢, а значит, S ¢ не является минимальным покрытием L. Что и требовалось доказать. выполняется, но S ¢ не является минимальным покрытием L. Значит, $ S²Ì S ¢, при этом S² – покрытие L. Тогда, согласно лемме 1,
выполняется, но S ¢ не является минимальным покрытием L. Значит, $ S²Ì S ¢, при этом S² – покрытие L. Тогда, согласно лемме 1,  . Значит, S² не может быть покрытием L, то есть получаем противоречие. Что и требовалось доказать.
. Значит, S² не может быть покрытием L, то есть получаем противоречие. Что и требовалось доказать. нагружена множеством L(vi).
нагружена множеством L(vi). определяет минимальное покрытие S ¢ множества L, однозначно соответствующее множе- ству V(E¢i)\{vi} вершин, если
определяет минимальное покрытие S ¢ множества L, однозначно соответствующее множе- ству V(E¢i)\{vi} вершин, если  , или множеству V(E¢i), если
, или множеству V(E¢i), если  .
. Значит, согласно лемме 1, множество
Значит, согласно лемме 1, множество  соответствующее V(E¢i), определяет покрытие множества L.
соответствующее V(E¢i), определяет покрытие множества L. однозначно соответствующее V(E¢i)\{vi}, определяет покрытие множества L.
однозначно соответствующее V(E¢i)\{vi}, определяет покрытие множества L. и
и  с соблюдением соответствующих условий). Что и требовалось доказать.
с соблюдением соответствующих условий). Что и требовалось доказать. "vÎV ®L(v)¹Æ,
"vÎV ®L(v)¹Æ,  , или множеству V(Ei), если
, или множеству V(Ei), если  .
. , можно сделать вывод о том, что данное покрытие также будет являться наименьшим. Что и требовалось доказать.
, можно сделать вывод о том, что данное покрытие также будет являться наименьшим. Что и требовалось доказать. определяется подмножество
определяется подмножество  . Если в результате получится непустое множество, делается вывод о том, что покрытия не существует, алгоритм закончен. В противном случае – переход к шагу 5.
. Если в результате получится непустое множество, делается вывод о том, что покрытия не существует, алгоритм закончен. В противном случае – переход к шагу 5. , для которого
, для которого  . Если
. Если  , осуществляется переход к шагу 8, иначе – к шагу 7.
, осуществляется переход к шагу 8, иначе – к шагу 7. ,
,  ,
,  ,
,  для всех
для всех  ,
,  , k ¬ k+1.
, k ¬ k+1. .
. определяется подмножество
определяется подмножество  .
. . Переход к шагу 9.
. Переход к шагу 9. определяет наименьшее покрытие множества L.
определяет наименьшее покрытие множества L. действий для вычисления нагрузки ребер полного графа. Такие вычисления выполняются (p–2) раза. Таким образом, грубая оценка O(p)=p3+p2.
действий для вычисления нагрузки ребер полного графа. Такие вычисления выполняются (p–2) раза. Таким образом, грубая оценка O(p)=p3+p2.
 . Таким образом, минимальное число устройств, для которых может быть решена задача покрытия при данных начальных условиях, равно 8.
. Таким образом, минимальное число устройств, для которых может быть решена задача покрытия при данных начальных условиях, равно 8.