Одним из направлений обеспечения качества продукции при серийном производстве является статистический контроль технологического процесса. При контроле независимых параметров исследуемого процесса стандарты предусматривают применение карт Шухарта и кумулятивных сумм. В случае контроля нескольких коррелированных параметров могут использоваться карты Хотеллинга и многомерных экспоненциально взвешенных скользящих средних, а также их модификации.
Многие работы зарубежных и отечественных авторов [1–3] рассматривают применение статистических методов для проведения контроля технологических процессов. Обнаружение нарушений процесса, как правило, проводится на основе выхода контролируемой статистики за заданные границы карты. Вместе с тем для одномерного контроля широко используются и другие критерии, в частности, поиск структур специального вида на карте Шухарта: если на карте имеет место структура (набор точек), вероятность появления которой близка к вероятности ложной тревоги, это свидетельствует о нарушении процесса.
Используются и карты с предупреждающими границами: попадание нескольких точек подряд между границами указывает на нарушение процесса. Современная компьютерная техника и ПО позволяют применить аналогичные подходы при многомерном статистическом контроле процесса.
Постановка задачи
Контролируются р параметров технологического процесса Х1, Х2, …, Хр. Предполагается, что р-мерный параметр имеет многомерное нормальное распределение Х ~ Nр(m, S) (m – вектор средних, S – ковариационная матрица). Результаты наблюдений анализируются с применением контрольной карты Хотеллинга [3–5]: для каждой t-й мгновенной выборки (t = 1, ..., m) рассчитывается статистика:
Tt2 = n( - m0)T S-1(
- m0)T S-1( - m0), (1)
- m0), (1)
здесь  – вектор средних в мгновенных выборках, `Xt = (
– вектор средних в мгновенных выборках, `Xt = (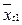 , ...,`xtp)T; `xtj – среднее значение в t-й мгновенной выборке по j-му показателю (j = 1, ..., p); m0 – вектор общих средних, m0 = (m1, ..., mp)T, mj =
, ...,`xtp)T; `xtj – среднее значение в t-й мгновенной выборке по j-му показателю (j = 1, ..., p); m0 – вектор общих средних, m0 = (m1, ..., mp)T, mj =  ; (2)
; (2)
S – оценка ковариационной матрицы S; компоненты ковариационной матрицы, определяющие рассеяние показателей качества и степень тесноты их связи, оцениваются по формуле
sjk =  , (3)
, (3)
j, k = 1, …, p.
Положение контрольной границы карты Хотеллинга определяется по формуле
Tkp2 =  (4)
(4)
где a – уровень значимости (вероятность ложной тревоги); F1–a(k1, k2) – квантиль F-распределения Фишера с числами степеней свободы в числителе k1, в знаменателе k2.
По аналогии с широко распространенными картами Шухарта процесс считается стабильным, если значения статистики (1) не превышают критическое значение (4): Шухартом было рекомендовано в качестве признаков вероятной разладки процесса рассматривать попадание точки, соответствующей контролируемому параметру, в область, находящуюся вне контрольных границ. На практике по мере расширения использования этих карт все чаще возникали случаи, когда все точки находились в зоне между контрольными границами, но по графику было видно, что процесс протекает нестабильно. Например, исследуемый процесс имеет явную тенденцию к росту или снижению, носит периодических характер, присутствует размещение множества последовательных точек по одну сторону от центральной линии и т.д. Вследствие этого возникла необходимость расширить перечень критериев, с помощью которых можно визуально оценить стабильность процесса. С этой целью было предложено выявлять структуры специального вида, или так называемые неслучайные структуры [6–8], то есть совокупности точек, вероятность образования которых сопоставима с вероятностью ложной тревоги (таких, появление которых при нормальном ходе процесса маловероятно).
Еще один подход для повышения эффективности контрольных карт может быть основан на использовании на карте предупреждающей границы. Для одномерных карт средних значений используется стандарт, предусматривающий возможность применения предупреждающей границы в трех вариантах принятия решения: процесс считается нестабильным, если в зоне между предупреждающей и контрольной границами находятся две, три или четыре точки подряд. Аналогичный подход возможен и при многомерном контроле [9].
Подсистема поиска специальных структур на карте Хотеллинга
 Опыт использования контрольных карт Хотеллинга пока недостаточен, чтобы можно было четко сформулировать основные критерии нестабильности процесса. Тем не менее, очевидно, что некоторые из критериев, используемых для интерпретации карт Шухарта, применимы и для карты Хотеллинга. По аналогии с рекомендуемой стандартом методикой обнаружения структур специального вида, свидетельствующих о нарушении процесса, на карте Шухарта область между горизонтальной осью t на карте Хотеллинга и контрольной границей (Upper Control Limit) UCL = Tkp2 разделена на три зоны – А, В и С (рис. 1).
Опыт использования контрольных карт Хотеллинга пока недостаточен, чтобы можно было четко сформулировать основные критерии нестабильности процесса. Тем не менее, очевидно, что некоторые из критериев, используемых для интерпретации карт Шухарта, применимы и для карты Хотеллинга. По аналогии с рекомендуемой стандартом методикой обнаружения структур специального вида, свидетельствующих о нарушении процесса, на карте Шухарта область между горизонтальной осью t на карте Хотеллинга и контрольной границей (Upper Control Limit) UCL = Tkp2 разделена на три зоны – А, В и С (рис. 1).
Существенный практический интерес может представлять анализ следующих структур специального вида, показанных на этом рисунке:
а) выход точки, соответствующей расчетному значению статистики Хотеллинга, за контрольную границу UCL;
б) тренд (сколько точек подряд на возрастание или на убывание в зависимости от количества контролируемых параметров могут рассматриваться как специальная структура, то есть вероятность появления такого количества точек соизмерима с вероятностью ложной тревоги);
в) приближение к оси абсцисс (зона С: в диапазоне до 1/3Ткр2) (сколько точек, расположенных подряд в этой зоне, в зависимости от количества контролируемых параметров могут рассматриваться как структура специального вида);
г) приближение к контрольной границе (зо- на А);
д) резкие скачки на карте – на величину kТкр2, (при каком k при заданном количестве контролируемых показателей р соответствующий скачок на карте может рассматриваться как специальная структура);
е) цикличность (сколько точек, расположенных в шахматном порядке, могут рассматриваться как структура специального вида).
Результаты расчета структур, свидетельствующих о возможном нарушении процесса [9], при контроле от двух до восьми параметров представлены в таблице 1.
Из данной таблицы следует, что, например, при контроле шести параметров в качестве структур специального вида могут рассматриваться тренд из 7 точек на карте Хотеллинга, или 10 точек подряд вблизи оси абсцисс, или 9 циклически расположенных точек и т.п.
Поиск соответствующих структур проводится с применением специальных алгоритмов. На рисунке 2 в качестве примера показана блок-схема алгоритма обнаружения приближения точки на карте Хотеллинга к оси абсцисс.

Подсистема построения карты с предупреждающей границей
Эффективность контрольных карт также может быть повышена путем использования предупреждающей границы, которое подразумевает разбиение области значений контролируемого параметра на три подобласти. Кроме обычных зон, характерных для стандартной карты Хотеллинга, при помощи предупреждающей границы выделяется до- полнительная область для переходного состояния процесса (зона W). Расположение нескольких точек подряд (от 2 до 4) в этой области может свидетельствовать о возможном нарушении процесса.
Определим положение контрольной границы UСL и предупреждающей UWL таким образом, чтобы попадание k точек подряд (k = 2, 3, 4) в об- ласть W свидетельствовало о наличии заданного опасного смещения среднего уровня процесса. Ре- зультат решения этой задачи методами теории цепей Маркова представлен в таблице 2, где дано положение контрольной UCL и предупреждающей UWL границ карты в зависимости от количества контролируемых показателей р и количества точек k, расположение которых подряд между границами карты свидетельствует о нарушении процесса на уровне значимости a = 0,005, наиболее распространенном при многомерном контроле [9].
Таблица 2
Положение контрольной и предупреждающей границ при 2, 3 и 4 точках подряд между границами
Table 2
The location of a control and warning limit with 2, 3 and 4 points in a row between limits
|
Количество параметров
|
2 точки
|
3 точки
|
4 точки
|
|
ucl
|
uwl
|
ucl
|
uwl
|
ucl
|
uwl
|
|
2
|
12,39
|
5,70
|
13,29
|
3,60
|
14,10
|
2,55
|
|
3
|
14,89
|
7,44
|
15,35
|
5,12
|
15,60
|
3,87
|
|
4
|
17,82
|
8,84
|
18,29
|
6,31
|
18,63
|
5,95
|
|
5
|
19,48
|
10,52
|
20,79
|
7,70
|
21,19
|
7,64
|
|
6
|
21,77
|
11,79
|
22,69
|
8,87
|
23,00
|
8,79
|
|
7
|
23,74
|
13,27
|
24,58
|
10,15
|
24,98
|
9,91
|
|
8
|
25,72
|
14,74
|
26,26
|
11,43
|
26,83
|
10,83
|
Программа обнаружения нарушений процесса
 Программа «Анализ специальных структур на карте Хотеллинга» (рис. 3) предназначена для диагностики нарушений при многомерном статисти- ческом контроле технологического процесса. Исходные данные включают количество контроли- руемых параметров, количество наблюдений в выборке, количество выборок, результаты измерений. В зависимости от степени коррелированности параметров их можно объединить в группы и строить карты для каждой группы.
Программа «Анализ специальных структур на карте Хотеллинга» (рис. 3) предназначена для диагностики нарушений при многомерном статисти- ческом контроле технологического процесса. Исходные данные включают количество контроли- руемых параметров, количество наблюдений в выборке, количество выборок, результаты измерений. В зависимости от степени коррелированности параметров их можно объединить в группы и строить карты для каждой группы.
Программа включает две подсистемы: для обнаружения структур специального вида на карте Хотеллинга; для построения карты с предупреждающей границей с поиском последовательности заданного числа точек, расположенных между пре- дупреждающей и контрольной границами. Программа обеспечивает диагностику процесса путем выявления соответствующих нарушений.
Разработанный программный продукт имеет следующие характеристики: тип операционной системы – Windows XP и выше; среда разработки – C#; использованы стандартные библиотеки MS Visual Studio 2013; размер программы – 3,42 Мб.
Численный эксперимент
Осуществлялся контроль десяти параметров Х1, Х2,…, Х10 – диаметры крышки датчика аэродинамических углов. Заданы допуски на изготовление: Х1 =  (Х1min=115,929 мм; Х1max=115,964 мм), Х2 = 113+0,35 (Х2min = 113 мм; Х2max = 113,35 мм), Х3 = 110е8 (Х3min = 109,928 мм; Х3max = 109,982 мм) и т.п. Для контроля предполагалось использовать многомерную карту Хотеллинга. Основная задача – проследить, как реагирует эта карта на возможные нарушения процесса.
(Х1min=115,929 мм; Х1max=115,964 мм), Х2 = 113+0,35 (Х2min = 113 мм; Х2max = 113,35 мм), Х3 = 110е8 (Х3min = 109,928 мм; Х3max = 109,982 мм) и т.п. Для контроля предполагалось использовать многомерную карту Хотеллинга. Основная задача – проследить, как реагирует эта карта на возможные нарушения процесса.
 На этапе анализа отлаженного процесса через равные промежутки времени делались замеры одной крышки (контроль по индивидуальным наблюдениям: n = 1). По результатам контроля 30 крышек построена корреляционная матрица (на рис. 4 жирным шрифтом выделены значимые корреляции), из которой следует, что все множество параметров может быть разбито на три подмножества по нали- чию корреляций: 1) Х1, Х3, Х10; 2) Х2, Х4, Х5, Х6; 3) Х7, Х8, Х9 (см. [2, 3]). По полученным данным были построены три карты Хотеллинга по каждому из рассматриваемых подмножеств: все три карты подтвердили стабильность процесса изготовления крышки. Основной целью этого этапа было определение положения контрольных границ карт для каждого подмножества параметров.
На этапе анализа отлаженного процесса через равные промежутки времени делались замеры одной крышки (контроль по индивидуальным наблюдениям: n = 1). По результатам контроля 30 крышек построена корреляционная матрица (на рис. 4 жирным шрифтом выделены значимые корреляции), из которой следует, что все множество параметров может быть разбито на три подмножества по нали- чию корреляций: 1) Х1, Х3, Х10; 2) Х2, Х4, Х5, Х6; 3) Х7, Х8, Х9 (см. [2, 3]). По полученным данным были построены три карты Хотеллинга по каждому из рассматриваемых подмножеств: все три карты подтвердили стабильность процесса изготовления крышки. Основной целью этого этапа было определение положения контрольных границ карт для каждого подмножества параметров.
При последующем мониторинге процесса с помощью карт Хотеллинга с найденными на предыдущем этапе контрольными границами по результатам наблюдений за 60 деталями нарушений процесса обнаружено не было. При этом для диагностики возможных нарушений процесса были использованы как карты с предупреждающей границей [9], так и обычные карты Хотеллинга с анализом неслучайных структур [8].
С целью выявления реакции различных модификаций карты Хотеллинга на возможные нарушения были смоделированы три типа нарушений:
1) смещение среднего уровня процесса по одному из показателей (с 10-го наблюдения до 20-го все значения Х1 увеличивались на некоторую постоянную величину, задаваемую в долях от стандартного отклонения: Х’1,k = Х1,k + as1; k = 10, 11, …, 20);
2) тренд процесса по всему подмножеству показателей; для моделирования этого нарушения каждое из значений Х1, Х3, Х10, начиная с 10-го наблюдения, последовательно увеличивалось на некоторую величину, например, для Х3: Х’3,10 = = Х3,10 + 0,2s3, Х’3,11 = Х3,11 + 0,4s3 и т.п.;
3) увеличение рассеяния данных по одному из контролируемых показателей.
 Первое из этих нарушений (смещение среднего уровня процесса) было выявлено с помощью карты Хотеллинга с предупреждающей границей (рис. 5), второе (тренд), как и ожидалось, проявилось в виде тренда на обычной карте Хотеллинга, третье (увеличение рассеяния) проявилось сразу в виде трех неслучайных структур: цикличности, резкого скачка и приближения значений статистики Хотеллинга к оси абсцисс (рис. 6). Заметим, что ни одно из смоделированных нарушений не проявилось бы, если бы была использована стандартная методика оценки статистической управляемости процесса, при которой нарушением процесса считается выход статистики Хотеллинга за контрольную границу. Как видно из результатов проведенных испытаний, выходов за контрольную границу при заданных нарушениях процесса нет.
Первое из этих нарушений (смещение среднего уровня процесса) было выявлено с помощью карты Хотеллинга с предупреждающей границей (рис. 5), второе (тренд), как и ожидалось, проявилось в виде тренда на обычной карте Хотеллинга, третье (увеличение рассеяния) проявилось сразу в виде трех неслучайных структур: цикличности, резкого скачка и приближения значений статистики Хотеллинга к оси абсцисс (рис. 6). Заметим, что ни одно из смоделированных нарушений не проявилось бы, если бы была использована стандартная методика оценки статистической управляемости процесса, при которой нарушением процесса считается выход статистики Хотеллинга за контрольную границу. Как видно из результатов проведенных испытаний, выходов за контрольную границу при заданных нарушениях процесса нет.
Итак, в работе предложена программа для интерпретации контрольных карт, реализующая методы, повышающие чувствительность многомерного контроля к возможным нарушениям технологического процесса. Результаты численного эксперимента на примере контроля десяти параметров датчика аэродинамических углов с использованием разработанного ПО свидетельствуют об эффективности этих методов.
Литература
1. Уилер Д., Чамберс Д. Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта. М.: Альпина Бизнес Букс, 2009. 409 c.
2. Айвазян С.А., Бухштабер В.М., Енюков И.С. Прикладная статистика // Классификация и снижение размерности. М.: Финансы и статистика, 1989. 607 с.
3. Montgomery D.C. Introduction to statistical quality control. NY: John Wiley and Sons, 2009, 754 р.
4. Ryan T.P. Statistical methods for quality improvement. NY, John Wiley and Sons, 2011, 687 р.
5. Bersimis S., Psarakis S., Panaretos J. Multivariate statistical process control charts: an overview. Quality and Reliability Eng. Intern., 2007, vol. 23, рр. 517–543.
6. Robert F., Marilyn K. Criteria for lack of control. Quality Management in Health Care, 2003, vol. 12, iss. 1, pр. 5–19.
7. Юнак Г.Л., Годлевский А.Н., Плотников А.Н. Об интерпретации серий на контрольных картах // Методы менеджмента качества. 2005. № 4. С. 41–48.
8. Клячкин В.Н., Кравцов Ю.А. Диагностика состояния объекта по наличию неслучайных структур на контрольной карте // Приборы и системы. Управление, контроль, диагностика. 2013. № 5. С. 44–50.
9. Клячкин В.Н., Кравцов Ю.А. Повышение эффективности статистического контроля многопараметрического технологического процесса на основе карты Хотеллинга с предупреждающей границей // Автоматизация и современные технологии. 2013. № 10. С. 35–37.



 - m0)T S-1(
- m0)T S-1(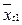 , ...,`xtp)T; `xtj – среднее значение в t-й мгновенной выборке по j-му показателю (j = 1, ..., p); m0 – вектор общих средних, m0 = (m1, ..., mp)T, mj =
, ...,`xtp)T; `xtj – среднее значение в t-й мгновенной выборке по j-му показателю (j = 1, ..., p); m0 – вектор общих средних, m0 = (m1, ..., mp)T, mj =  ; (2)
; (2) , (3)
, (3) (4)
(4)


 (Х1min=115,929 мм; Х1max=115,964 мм), Х2 = 113+0,35 (Х2min = 113 мм; Х2max = 113,35 мм), Х3 = 110е8 (Х3min = 109,928 мм; Х3max = 109,982 мм) и т.п. Для контроля предполагалось использовать многомерную карту Хотеллинга. Основная задача – проследить, как реагирует эта карта на возможные нарушения процесса.
(Х1min=115,929 мм; Х1max=115,964 мм), Х2 = 113+0,35 (Х2min = 113 мм; Х2max = 113,35 мм), Х3 = 110е8 (Х3min = 109,928 мм; Х3max = 109,982 мм) и т.п. Для контроля предполагалось использовать многомерную карту Хотеллинга. Основная задача – проследить, как реагирует эта карта на возможные нарушения процесса.

