Программные продукты и системы

Эмпирический риск обычно вычисляется как среднее арифметическое от значений параметрической функции потерь. Эмпирическая оценка средних потерь как среднее арифметическое адекватна со статистической точки зрения, если потери распределены по нормальному закону. Однако даже для нормального закона среднее арифметическое не является робастной оценкой среднего значения, в то время как медиана позволяет оценивать эмпирическое среднее при наличии выбросов. Поэтому для построения параметрических регрессионных зависимостей также используются эмпирические оценки среднего при помощи медианы, несмотря на то, что использование медианы делает процедуру настройки параметров регрессионной зависимости более медленной.

В условиях выбросов также используют оценки квантилей, когда искажения в распределении потерь составляют меньше 50 %. Это позволяет при настройке параметров при помощи медианы не терять полезную часть распределения потерь, которая расположена выше значения медианы, разделяющей упорядоченный по возрастанию набор потерь на две равные части.

Классический метод эмпирического риска

Задача поиска параметрической регрессионной зависимости y = f(x, w) между входами x и скалярным выходом y является одной из классических задач машинного обучения. Имеются конечный на­бор входов и набор известных значений на выходе: : k = 1, …, N}. Требуется найти такой набор параметров w*, при котором функция f*(x) = f(x, w*) адекватно представляет зависимость между y и x на множестве

В качестве меры адекватности f* часто используют эмпирический риск. Набор параметров w*, задающий адекватную параметрическую зависимость, должен минимизировать величину эмпирического риска.

Эмпирический риск обычно вычисляется как среднее арифметическое от значений параметрической функции потерь , где ℓk(w) = ℓk(rk(w)), где ℓ(r) – функция потерь; – функция невязки между значением функции f и ожидаемым значением в k-й точке. Например:

·      разность: ;

·      абсолютная разность: ;

·      несимметричная абсолютная разность: , где

·     относительная разность: при условии, что значения 𝑦 отделены от нуля, или .

Функция потерь – это неотрицательная функция, которая имеет единственный минимум, так что ℓ(0) = min ℓ(r) = 0. Например:

·      абсолютная:;

·      квадратичная: ;

·      Хьюбера:

·      Тьюки (для простоты приведена производная функции):

·  несимметричная абсолютная:

·  несимметричная квадратичная:

Здесь c > 0, 0 < a < 1.

Со статистической точки зрения оценка потерь при помощи среднего арифметического является адекватной, если потери распределены по нормальному закону. Однако если в действительности потери распределены по другому закону, оценка средних потерь должна осуществляться другим способом. Но даже в случае нормально распределенных потерь среднее арифметическое не является устойчивым по отношению к выбросам в эмпирическом распределении. В этом случае существенно более адекватной оценкой является, например, медиана или квантили.

Среднее арифметическое, медиана и квантили – примеры усредняющей агрегирующей функции, поэтому в общем случае средние потери можно вычислять при помощи усредняющих агрегирующих функций.

Усредняющие агрегирующие функции

Пусть – сегмент ; – множество всех конечных последовательностей {z1, …, zN}Ï.

Определение. Агрегирующая функция – это отображение M: ®, которое удовлетворяет следующим требованиям:

·      ;

·      , то .

Последнее требование – требование монотонности агрегирующей функции.

Агрегирующая функция M симметричная, если M{z1, …, zN}= M{zp(1), …, zp(N)} для любой перестановки π ряда чисел 1, …, N.

Усредняющие агрегирующие функции, по определению, удовлетворяют дополнительному требованию min{z1, …, zN} ≤ M{z1, …, zN} ≤ max{z1, …, zN}.

Основные понятия и основные свойства агрегирующих функций подробно описаны в [2–4].

Существует универсальный способ определения усредняющих агрегирующих функций [5]. Для их определения используются штрафные функции.

Определение. Функция P{z1, …, zN, u} является штрафной, если удовлетворяет следующим требованиям:

·  P{z1, …, zN, u} ³ 0 для всех u и z1, …, zN;

·  P{z1, …, zN, u} = 0, только если z1 = … = = zN =u ;

·  для всех z1, …, zN множество Mz1, …, zN = = {u: P(z1, …, zN, u) = Pmin(z1, …, zN)}, где Pmin(z1, …, zN) =, является синглетоном или связным сегментом.

Всякую усредняющую агрегирующую функцию можно определить на основе некоторой штрафной функции P следующим образом: Mp{z1, …, zN} =, если Mz1, …, zN – синглетон и Mp{z1, …, zN} = , если Mz1, …, zN – сегмент с концами 𝑎 и 𝑏. Заметим, что формально в последнем случае можно было бы выбрать любое значение из интервала (𝑎, 𝑏) или некоторое значение из (𝑎, 𝑏), зависящее от P.

Далее рассмотрим разновидность штрафных функций, которые являются суммами функций несходства:

P(z1, …, zN, u) = , (1)

где 𝑝(𝑧, 𝑢) – функция несходства (dissimilarity function). Функция несходства определяется следующим образом.

Определение. Функция 𝑝(𝑧, 𝑢) является функцией несходства, если удовлетворяет следующим условиям:

·      p(𝑧, 𝑢) = 0 Û 𝑧 = 𝑢;

·      p(𝑧1, 𝑢) ³ p(𝑧2, 𝑢), когда 𝑧1 ³ 𝑧2 ³ u или 𝑧1 ≤ 𝑧2 ≤ u.

Агрегирующую функцию, определенную на базе штрафной функции вида (1), будем обозначать Mp.

Статистическая интерпретация Mp{z1, …, zN} на основе принципа максимума правдоподобия следующая: если случайная величина z распределена по вероятностному закону , где – среднее значение, то Mp{z1, …, zN} является эмпирической оценкой

Уникальность минимума Pz1, …, zN(u) = P(z1, …, zN, u) и монотонность Mp{z1, …, zN} гарантированы, когда

p(𝑧, 𝑢) = G(h(z)– h(u)), (2)

где G: – непрерывная строго выпуклая функция; h(u) – строго монотонная функция [4, 5].

Приведем примеры известных усредняющих агрегирующих функций, которые можно определить таким образом.

·      Среднее арифметическое получается при p(z, u) = (zk–u)2: M{z1, …, zN} =

·      Медиана

получается при p(zk – u) = ½zk – u½:

,

где z(1), …, z(N) – множество z1, …, zN, упорядоченное в порядке неубывания.

·      Квантиль a Qa{z1, …, zN} получается при p(z, u) = ½zk – u½a:

,

где

·        Экспектиль a

,

где

·        Среднее по Колмогорову

получается при p(u, zk) = (g(u) – g(zk))2:

.

·        Масштабированная медиана

получается при p(u, zk) =½g(u) – g(zk)½:

.

Поиск значения Mp{z1, …, zN} можно осуществ- лять методом полного градиента или методом Ньютона. В первом случае на каждом шаге текущая оценка искомого значения обновляется по следующему правилу: , где .

Во втором случае обновление осуществляется по правилу

, где .

Параметр темпа обучения ht в этих методах может быть постпостоянным или выбираться при помощи одного из методов поиска типа line search.

При больших N удобнее применять стохастические варианты этих алгоритмов. Например, такие алгоритмы, в основе которых лежит такая же схема, как и в основе SAG [6, 7].

В первом случае обновление будет осуществляться по правилу , где k(t) – номер случайно выбранного значения из z1, …, zN на шаге t. При этом

Среднее значение производной можно обновлять на каждом шаге по простому правилу

Во втором случае обновление осуществляется по следующему правилу: где и .

При этом

а

Значение отношения Gt/Ht обновляется на каждом шаге по простому правилу:

Псевдокод алгоритма – Алг. 1.

Algorithm 1. Алгоритм типа SAG для вычисления значения Mg{z1, …, zN}.

Инициализировать u0

, k = 1, …, N

, k = 1, …, N

G¬G1+ …+ GN

If используется схема Ньютона then

, k = 1, …, N,

H¬H1+ …+ HN

end if

t¬0

repeat

k ¬ k(t)

If используется схема Ньютона then

else

end if

t ¬ t + 1

until значение ut не стабилизируется.

От эмпирического риска к агрегированному

Усредняющие агрегирующие функции уже использовались в [8, 9] для построения функционалов потерь в контексте задачи построения операций над алгоритмами классификации и регрессии, которые сохраняют свойство корректности алгоритмов. Применим их теперь для оценки средних потерь: , где усредняющая агрегирующая функция Mp определяется на основе штрафной функции вида (1):

Оптимальный набор параметров w* доставляет минимум : .

Если p(z, u) имеет частные производные до второго порядка включительно, то

где .

Тогда

где .

Поиск оптимального набора w можно осуществлять при помощи следующего варианта про- цедуры полного градиента. Правило обновления вектора параметров имеет вид

Обновления вектора параметров осуществляются до тех пор, пока значения wt и не стабилизируются.

Если p(z, u) = G(z – u) – частный случай (2), то

,

где , причем a1(w) + …+ aN(w) = 1.

Нетрудно заметить, что в этом случае процедура градиентного спуска похожа на процедуру поиска минимума взвешенного среднего от потерь с числовыми весами. Однако в данном случае веса являются функциями от – отклонений между агрегированным средним от потерь и текущими потерями. Если G(z–u) = (z–u)2/2, то ak(w) = 1/N, что соответствует среднему арифметическому от потерь или значению эмпирического риска.

Псевдокод алгоритма настройки параметров w на основе метода полного градиента – алгоритм PBFG. Приведенный алгоритм не является оптимальным с вычислительной точки зрения, так как на каждом шаге итерации необходимо решать задачу поиска минимума функции для вычисления значения агрегированного среднего значения. Поэтому рассмотрим другой итерационный алгоритм, который ищет значения w* и Mp{ℓ1(w*), …, ℓN(w*)} одновременно.

Algorithm PBFG. Алгоритм полного градиентного спуска на базе агрегирующей функции

t ¬ 0

Инициализировать w0

repeat

t ¬ t+1

until {u} и {wt} не стабилизируется.

Алгоритм стохастического усредненного градиента на базе агрегирующих функций

Поскольку данный усредненный градиент является взвешенной суммой градиентов от соответствующих потерь, можно применить метод, лежащий в основе алгоритма SAG (Stochastic Average Gradient) [6, 7]. Построим на основе этого метода алгоритм PBSAG (Penalty Based Stochastic Average Gradient) стохастически усредненного градиента на базе усредняющей верной агрегирующей функции. Схема адаптации параметров w и u имеет вид

, ,

где .

Значение для поиска минимального значения усредняющей агрегирующей функции Mp может обновляться в соответствии с одним из следующих правил: или в зависимости от используемого метода: градиентного спуска или Ньютона. Векторы из набора обновляются по следующему правилу:

Значения из наборов и обновляются по следующим правилам:

Algorithm PBSAG. Алгоритм стохастически усредненного градиента на базе усредняющей функции

t ¬ 0

Инициализировать w0

for kÎ{1, …, N} do

end for

G ¬ G1 + … +GN

H ¬ H1 + … + HN

Q ¬ Q1 + … + QN

repeat

k = k(t)

if используется схема Ньютона then

else

end if

v

v

until {ut} и {wt} не стабилизируются

Алгоритму PBSAG на каждом шаге необходимо хранить по одному градиентному вектору и по два значения на каждый пример из обучающего набора данных, то есть N(m + 2) вещественных чисел, где m – ранг вектора параметров w. Поэтому его следует применять, если есть память для хранения такого объема данных.

Нетрудно заметить, что при p(z, u) = (z–u)2/2 схема алгоритма PBSAG редуцируется к схеме алгоритма SAG: , где

Таким образом, схема алгоритма PBSAG является естественным обобщением схемы алгоритма SAG [6, 7], когда для вычисления средних потерь используется усредняющая агрегирующая функция, основанная на штрафной, вместо среднего арифметического.

Примеры применения PBSAG

Рассмотрим применение PBSAG с использованием аппроксимированного варианта LMS [10, 11] для поиска линейной регрессии в условиях выбросов. В стандартном алгоритме LMS ищется минимум медианы квадрата ошибки:

PBSAG нельзя применить, когда M является медианой. Однако ее можно заменить на суррогат медианы, который асимптотически эквивалентен ей.

Определение. pa(z – u) определяет суррогат медианы, асимптотически эквивалентный медиане, если для некоторого a*

.

Рассмотрим пример:

где a*=0,

Соответствующую ей усредняющую агрегирующую функцию будем называть a-медианой:

Другой пример суррогата можно построить на основе следующей функции несходства:

. (3)

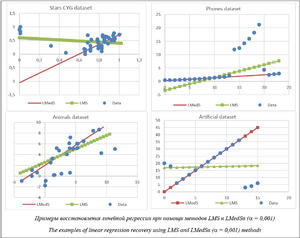
На рисунке представлены примеры применения алгоритма PBSAG. Они показывают способность метода и алгоритма PBSAG на базе усредняющего верного агрегирующего функционала, аппроксимирующего медиану (3), восстановливать линейную регрессионную зависимость в случае, когда исходные данные содержат выбросы.

Заключение

В данной работе эти функции используются для оценки средних потерь, где усредняющая агрегиру- ющая функция определяется на основе штрафной функции. В результате процедура градиентного спуска становится аналогичной процедуре поиска минимума взвешенного среднего от потерь с числовыми весами. Это позволяет построить алгоритм PBSAG – стохастически усредненного градиента на базе усредняющей верной агрегирующей функции. Предложенный алгоритм, реализующий метод минимизации эмпирического риска, позволяет справляться с задачей восстановления линейной регрессионной зависимости в случае, когда исходные данные содержат выбросы. Данное свойство алгоритма продемонстрировано на соответствующих примерах.

(Работа выполнена при поддержке гранта РФФИ № 15-01-03381 и гранта ОНИТ РАН).

Литература

1.     Vapnik V. The nature of statistical learning theory (Information Science and Statistics). Springer-Verlag. NY, 2000, 314 p.

2.     Mesiar R., Komornikova M., Kolesarova A., Calvo T. Aggregation functions: a revision. In H. Bustince, F. Herrera, J. Montero, eds. (Fuzzy Sets and Their Extensions: Representation, Aggregation and Models). Springer, Berlin, Heidelberg, 2008.

3.     Grabich M., Marichal J.-L., Pap E. Aggregation functions (Encyclopedia of Mathematics and its Applications), Cambridge Univ. Press, 2009, no. 127.

4.     Beliakov G., Sola H., Calvo T. A practical guide to averaging functions. Springer, 2016, 329 p.

5.     Calvo T., Beliakov G. Aggregation functions based on penalties. Fuzzy Sets and Systems. 2010, vol. 161, no. 10, pp. 1420–1436.

6.     Le Roux N., Schmidt M., Bach F. A stochastic gradient method with an exponential convergence rate for finite training sets. 2012. URL: http://arxiv.org/abs/1202.6258 (дата обращения: 05.10.2016).

7.     Schmidt M., Le Roux N., Bach F. Minimizing finite sums with the stochastic average gradient. 2013. URL: http://arxiv.org/ abs/1309.2388 (дата обращения: 05.10.2016).

8.     Shibzukhov Z.M. Correct aggregate operations with algorithms, Pattern Recognition and Image Analysis, 2014, vol. 24, no. 3, pp. 377–382.

9.     Shibzukhov Z.M. Aggregation correct operations on algorithms. Dokl. Math. 2015, vol. 91, no. 3, pp. 391–393.

10.   Rousseeuw P.J. Least median of squares regression. Jour. of the American Statistical Association, 1984, no. 79, pp. 871–880.

11.   Rousseeuw P.J., Leroy A.M. Robust regression and outlier detection. NY, John Wiley and Sons, 1987.