В современном мире рост производительности при обработке большого количества разнообразной информации достигается только в тех случаях, когда часть интеллектуальной нагрузки берут на себя компьютеры. Одним из направлений исследований в области искусственного интеллекта [1, 2] являются интеллектуальные информационные системы, которые находятся на пике исследовательской активности, практики прикладного приме- нения и коммерциализации. Они широко вошли в разные области промышленности, экономики, медицины и т.д. Интеллектуальные информационные системы сосредоточили в себе наиболее наукоемкие технологии с высоким уровнем автоматизации процессов не только подготовки информации для принятия решений, но и выработки вариантов решений, опирающихся на полученные информационной системой данные.
Проблемы эффективного применения, использования, внедрения интеллектуальных систем определяют сложность подходов к классификации задач искусственного интеллекта и решаются в рамках различных направлений исследований, основанных на близких моделях, методах и алгоритмах. К таким исследованиям относятся распознава- ние образов, машинное обучение, машинный пере- вод, интеллектуальный анализ данных и др. [2].
Одной из базовых апорий интеллектуального анализа данных [3] являются технологии распознавания образов [4–6]. Распознавание образов – класс задач, связанных с определением принадлежности объекта к одному из классов объектов. Распознавание образов можно рассматривать как классификацию объектов. Сложность и многофакторность проблемы распознавания образов, разнообразие проблемных областей и категорий задач, отсутствие универсальных методов решения задач распознавания приводят к тому, что традиционная методология разработки систем распознавания, как правило, не позволяет достигнуть требуемой эффективности результатов в рамках промышленного применения.
В настоящее время существует значительное противоречие, обусловленное уровнем развития формального аппарата теории распознавания образов, сравнительной ограниченностью и узкой направленностью большинства из существующих прикладных систем распознавания. Данное противоречие частично может быть преодолено путем разработки интегрированных многофункциональ- ных автоматизированных информационных систем распознавания, ориентированных на решение широкого класса задач и допускающих адаптацию и настройку на новую предметную область и категорию задач.
Описание программы. В рамках исследований по тематике «Web-инструментарий машинного обучения» в качестве прототипа облачного ресурса разработана программа «Web-инструментарий распознавания образов на основе расширяющейся библиотеки методов машинного обучения» [7, 8]. Программа может быть использована для принятия решений широким кругом лиц, в том числе студентами, преподавателями, бизнесменами, специалистами в различных областях.
В базовой версии программы реализован класс методов прецедентов как пользующаяся популярностью классика в области data-mining. Методы прецедентов состоят из следующих циклов: 1) извлечение похожего прецедента из библиотеки; 2) использование выбранного прецедента для построения решения; 3) проверка полученного решения; 4) занесение решения как нового прецедента в библиотеку. Таким образом, системой накапливается опыт (прецеденты) и реализуется машинное обучение, что способствует повышению качества принимаемого решения [9].
Главным достоинством методов прецедентов является их высокая эффективность для множества задач с точки зрения достоверности результата и компактности алгоритмов анализа, а главным недостатком – требование значительных вычислительных ресурсов. Особенно это актуально при работе с большими объемами данных.
 В качестве основных алгоритмов анализа в программе (рис. 1) были реализованы такие методы прецедентов, как метод k-ближайших соседей, метод потенциальных функций, метод эталонов, метод коррекционных приращений, метод наименьших среднеквадратических ошибок, метод наивный байесовский. Методы основаны на алгоритмах метрической классификации и оценивании сходства объектов, для всех методов характерно наличие обучающей выборки.
В качестве основных алгоритмов анализа в программе (рис. 1) были реализованы такие методы прецедентов, как метод k-ближайших соседей, метод потенциальных функций, метод эталонов, метод коррекционных приращений, метод наименьших среднеквадратических ошибок, метод наивный байесовский. Методы основаны на алгоритмах метрической классификации и оценивании сходства объектов, для всех методов характерно наличие обучающей выборки.
Программа развивает концепцию облачных вычислений и осуществляет распознавание образов на основе методов машинного обучения посредством реализации web-сервиса и использования web-технологий. Компоненты web-технологий в программе реализованы с помощью сервлетов, которые расширяют функциональность web-серверов. Выбор в пользу сервлетов обусловлен тем, что они позволяют создавать платформенно-независимый код, предоставляют возможность масштабирования программы и могут выполняться параллельно в рамках одного процесса на сервере.
Алгоритмы распараллеливания методов прецедентов. Борьба за эффективное использование вычислительных ресурсов привела к появлению технологий распределенных систем и параллельных вычислений [10, 11], в частности, grid- и интернет-технологий. Grid-система строится по принципу клиент–сервер, состоит из одного или нескольких компьютеров-серверов и множества компьютеров-клиентов свободной конфигурации и представляет собой эффективную для распараллеливания структуру вычислительных ресурсов.
Так как у методов прецедентов наличие обучающей выборки обязательно, в их работе можно выделить два последовательных этапа: этап обучения и этап распознавания. Рассмотрим схемы реализации этих этапов на одном компьютере (базовом для расчетов компьютере K0) более подробно. В рамках исследований множества обучающих и классифицируемых объектов представлены как отдельные файлы, а объекты в них – как строки атрибутов. Файл с обучающими объектами (Fобуч.) содержит w объектов (строк), а файл с классифицируемыми объектами (Fклассиф.) имеет m объектов.
Этап обучения. Этап обучения на K0 компьютере заключается в следующем: 1) компьютер K0 поочередно считывает один из w обучающих объектов (qk-й объект) из файла Fобуч. и подает его на вход классификатора; 2) классификатор, получив qk-й обучающий объект, строит на его основе решение с учетом меры близости применяемого метода прецедента. После построения решения на основе всех w объектов из файла Fобуч. на выходе классификатора образуется система решающих правил, способная определить класс классифицируемого объекта.
 Обозначим время обучения классификатора на qk-м объекте как Tобуч.(qk). Тогда время обучения на основе файла Fобуч. на K0 компьютере рассчитывается как суммарное время обучения классификатора на w обучающих объектах:
Обозначим время обучения классификатора на qk-м объекте как Tобуч.(qk). Тогда время обучения на основе файла Fобуч. на K0 компьютере рассчитывается как суммарное время обучения классификатора на w обучающих объектах:
 . (1)
. (1)
Этап распознавания. Этап распознавания на K0 компьютере (рис. 2) заключается в следующем: 1) компьютер K0 поочередно занимается предобработкой одного из m классифицируемых объектов (xk-й объект) из файла Fклассиф.; обозначим этот этап как функцию Fпредобр.(xk), а время, затраченное на предобработку xk-го объекта, как Tпредобр.(xk); 2) затем xk-й объект поступает на вход системы решающих правил, которая определяет его класс (ck); обозначим этот этап как функцию Fопред.(xk), а время, затраченное на определение класса xk-го объекта, как Tопред.(xk); 3) в заключение класс xk-го объекта (ck) добавляется в выходной файл, этот этап обозначим как функцию Fдобав.(ck), а время, затраченное на добавление ck-го класса, как Tдобав.(ck).
Тогда время распознавания на K0 компьютере рассчитывается по формуле
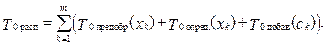 (2)
(2)
Или, сгруппировав время по функциям, перепишем формулу (2):
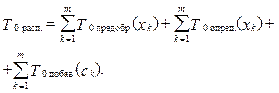 (3)
(3)
Рассмотрим и проанализируем входящие в распознавание классифицируемых объектов процессы на K0 компьютере более подробно.
Процесс предобработки (функция Fпредобр.(xk)) на K0 компьютере состоит из двух этапов: 1) чтение xk-го объекта из файла Fклассиф.; обозначим чтение как функцию Fчтен.(xk), а время, затраченное на чтение xk-го объекта, как Tчтен.(xk); 2) запись xk-го объекта в выходной файл; обозначим запись как функцию Fзап.(xk), а время, затраченное на запись прочитанного xk-го объекта в выходной файл, как Tзап.(xk). Другими словами, время предобработки xk-го объ- екта на K0 компьютере определяется по формуле T0 предобр.(xk) = T0 чтен.(xk) + T0 зап.(xk).
Процесс определения класса специфичен для каждого из методов прецедентов, следовательно, время определения класса будет зависеть от примененного метода прецедента.
Процесс добавления результатов распознавания xk-го объекта в виде класса ck в выходной файл (функция Fдобав.(ck)) на одном K0 компьютере представляет собой функцию записи класса ck в конец выходного файла и рассчитывается следующим образом: T0 добав.(ck) = T0 зап.(сk).
Дополнительно введем два параметра: T0 средн. опред. и V0 средн. опред..
T0 средн. опред. – среднее время определения класса на K0 компьютере одного классифицируемого объекта:  .
.
V0 средн. опред. – средняя скорость определения класса объектов на K0 компьютере, то есть сколько классов объектов (число может быть нецелым) K0 компьютер определяет в единицу времени:
 . (4)
. (4)
Стоит отметить, что T0 средн. опред. и V0 средн. опред.. для всех объектов распознавания на K0 компьютере одинаковы, потому что порядок и количество операций для определения класса любого объекта одинаково, а скорость выполнения операции на K0 компьютере постоянна. Следовательно, чем больше скорость выполнения операции на K0 компьютере (производительность), тем меньше T0 средн. опред. и больше V0 средн. опред..
С учетом формулы (4) формулу (3) можно переписать так:
 (5)
(5)
Реализация параллельной вычислительной системы. Анализ основных процессов этапа распознавания и формулы (2) позволяет сделать вывод, что распознавание xk-го объекта никак не связано с распознаванием остальных классифицируемых объектов. Таким образом, распознавание объектов можно делать параллельно на n компьютерах, а записывать результаты распознавания в один выходной файл на центральном сервере. Другими словами, подключив n компьютеров к K0, можно получить вычислительную сеть, где K0 будет играть роль центрального сервера.
На рисунке 3 показана структура такой параллельной вычислительной системы из n компьютеров K1, K2, Kn и сервера K0, где функции Fпредобр.(xk), Fдобав.(ck) такие же, как в случае одного компьютера K0, потому что сервером является K0 компьютер. Особую роль в вычислительной системе играет функция распределения m классифицируемых объектов между n компьютерами, то есть функция P(m, n). Функция P(m, n) по мере того, как компьютеры закончили обработку одного объекта, передает им по заданному алгоритму новый классифицируемый объект для распознавания. Совокупность объектов для обработки на Ki-м компьютере обозначим как Xi = .
Суть работы такой вычислительной системы заключается в следующем: 1) сервер поочередно занимается предобработкой одного из m классифицируемых объектов (xk-й объект) из файла  и передает его функции P(m, n); 2) функция P(m, n) распределяет полученный xk-й объект на Ki-й компьютер согласно алгоритму реализации функции P(m, n); 3) после распознавания на выходе Ki-го компьютера образуется результат в виде класса ck; 4) сервер, получив класс ck, добавляет его в выходной файл с помощью функции Fдобав.(ck).
и передает его функции P(m, n); 2) функция P(m, n) распределяет полученный xk-й объект на Ki-й компьютер согласно алгоритму реализации функции P(m, n); 3) после распознавания на выходе Ki-го компьютера образуется результат в виде класса ck; 4) сервер, получив класс ck, добавляет его в выходной файл с помощью функции Fдобав.(ck).
Необходимо учитывать, что скорость распознавания (Vi средн. опред.) у компьютеров может быть различной, так как компьютеры могут обладать разной производительностью. Отсортируем компьютеры по скорости Vi средн. опред. в порядке возрас- тания. Если скорости Vi средн. опред. у нескольких компьютеров одинаковые, будем сортировать их в порядке возрастания индексов i (компьютеры представлены в виде Ki).
 Введем обозначение Ki мин. произ. для отсортиро- ванного по возрастанию скорости Vi средн. опред. ряда компьютеров, а их скорость Vi средн. опред. обозначим Vi мин. произ. средн. опред.. Например, K1 мин. произ. – первый компьютер в ряду, то есть компьютер, у которого скорость V1 мин. произ. средн. опред. ≤ Vi мин. произ. средн. опред., где 1 < i ≤ n, то есть скорости Vi средн. опред. меньше, чем у него, среди n компьютеров нет.
Введем обозначение Ki мин. произ. для отсортиро- ванного по возрастанию скорости Vi средн. опред. ряда компьютеров, а их скорость Vi средн. опред. обозначим Vi мин. произ. средн. опред.. Например, K1 мин. произ. – первый компьютер в ряду, то есть компьютер, у которого скорость V1 мин. произ. средн. опред. ≤ Vi мин. произ. средн. опред., где 1 < i ≤ n, то есть скорости Vi средн. опред. меньше, чем у него, среди n компьютеров нет.
Дополнительно отметим, что K2 мин. произ. – второй компьютер в ряду, то есть, если из множества n компьютеров исключить K1 мин. произ., то скорости Vi средн. опред. меньше V2 мин. произ. средн. опред. среди множества n–1 компьютеров не будет.
Рассчитаем время распознавания файла Fклассиф. такой системой. Исследовав этапы работы параллельной вычислительной системы из n компьютеров, можно сделать вывод, что время распознавания будет зависеть от работы самого долгого по времени звена. Обозначим компьютер из этого звена как Kдолг. звена, количество объектов, поступивших на Kдолг. звена, как p долг. звена, скорость Vсредн. опред. компьютера Kдолг. звена как V долг. звена средн. опред.. Стоит заметить, что компьютер Kдолг. звена может не совпадать с K1 мин. произ..
Для расчетов времени распознавания также необходимо отметить следующее: 1) как говорилось выше, Ki-й компьютер получает объект для распознавания только после распознавания xk-го объекта и записи сервером его класса в выходной файл; 2) из-за того, что чтение объектов из файла Fклассиф. происходит последовательно, а распознавание параллельно, может возникнуть ситуация ожидания чтения Ki-м компьютером своего объекта для распознавания, то есть Ki-й компьютер вынужден ждать, пока остальные компьютеры не прочитают свои объекты; 3) запись в выходной файл тоже происходит последовательно, что предполагает наличие возможности ожидания Ki-м компьютером своей очереди записи. Другими словами, необходима синхронизация процессов распознавания.
Заметим, что из-за синхронизации компьютер Kдолг. звена может оказаться последним в очереди на чтение и ему придется ждать, пока все n–1 компьютеры не прочитают свои объекты из файла Fклассиф.. То же самое относится и к записи класса в выходной файл. С учетом этих условий рассчитаем время распознавания файла Fклассиф.:
 (6)
(6)
где  – сумма времени ожидания, пока все n–1 компьютеры не прочитают свои объекты, и времени чтения компьютером Kдолг. звена своего объекта;
– сумма времени ожидания, пока все n–1 компьютеры не прочитают свои объекты, и времени чтения компьютером Kдолг. звена своего объекта;  – время определения класса одного классифицируемого объекта компьютером Kдолг. звена;
– время определения класса одного классифицируемого объекта компьютером Kдолг. звена; 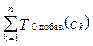 – сумма времени ожидания, пока все n–1 компьютеры не запишут свои классы, и времени записи компьютером Kдолг. звена класса своего объекта; p долг. звена – количество объектов, которое распознает компьютер Kдолг. звена.
– сумма времени ожидания, пока все n–1 компьютеры не запишут свои классы, и времени записи компьютером Kдолг. звена класса своего объекта; p долг. звена – количество объектов, которое распознает компьютер Kдолг. звена.
Или, сгруппировав время по функциям, перепишем формулу (6):
 (7)
(7)
Необходимо принять во внимание, что от реализации алгоритма распределения объектов функцией P(m, n) будет зависеть и результат обработки, так как от функции P(m, n) зависит число pдолг. звена. Рассмотрим несколько вариантов реализации этой функции.
Первый вариант. Функция P(m, n) равномерно распределяет классифицируемые объекты между n компьютерами по следующему принципу: Xi = .
Рассчитаем количество классифицируемых объектов, которые получит каждый компьютер. Для этого учтем тот факт, что m (количество объектов) может быть не кратным числу n (количество компьютеров). Тогда некоторые компьютеры получат меньше объектов, а другие больше объектов (pмакс.). Рассчитаем максимальное количество объектов, которые получат компьютеры при условии, что m ≥ n:
 , (8)
, (8)
где 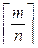 – округление числа m/n до целого числа в большую сторону.
– округление числа m/n до целого числа в большую сторону.
Чтобы воспользоваться формулой (7), необходимо определить Kдолг. звена, а точнее, его скорость Vдолг. звена средн. опред. и количество объектов, которое он распознает. Из (8) и определения K1 мин. произ. можно сделать вывод, что Kдолг. звена = K1 мин. произ., Vдолг. звена средн. опред. = V1 мин. произ. средн. опред., а pдолг. звена= = pмакс.. Тогда по формуле (7) рассчитаем время распознавания файла Fклассиф. при равномерном распределении объектов между n компьютерами:
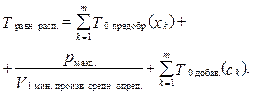 (9)
(9)
Проанализировав формулу (9), можно сделать вывод, что скорость V1 мин. произ. средн. опред. обратно пропорциональна времени распознавания.
Выразим V1 мин. произ. средн. опред. через V0 средн. опред.: V1 мин. произ. средн. опред. = α * V0 средн. опред. Параметр α показывает, во сколько раз K1 мин. произ. медленнее K0, если 0 < α < 1, и быстрее, если α > 1.
Перепишем формулу (9) с учетом введенного параметра a:
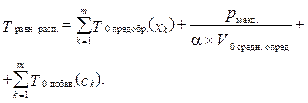 (10)
(10)
Рассмотрев формулу (10), можно заметить, что первое и третье слагаемые всегда будут вносить одинаковый вклад в общее время распознавания несмотря на изменение параметра α. Другими словами, как бы ни изменялся параметр α, сумма 
 всегда будет нижней границей времени распознавания.
всегда будет нижней границей времени распознавания.
Исследуем влияние параметра α на время распознавания:
1) α = 1, тогда V1 мин. произ. средн. опред. = V0 средн. опред., а общее время распознавания, согласно формуле (10), является суммой времени распознавания pмакс. объектов, времени предобработки m объектов и времени добавления результатов распознавания m объектов в выходной файл:

2) α = 2, тогда V1 мин. произ. средн. опред. = = 2 * V0 средн. опред., а общее время распознавания рассчитывается следующим образом:
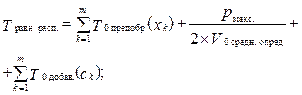
3) раз V1 мин. произ. средн. опред. обратно пропорционально общему времени распознавания, определим αlimit, при котором T0 расп. = Tравн. расп., то есть не будет выигрыша по времени при распознавании; приравняв формулы (5) и (10), определим αlimit = pмакс./m.
Рассмотрев формулу (10) и сравнив между собой время распознавания при различных значениях параметра α, можно сделать следующие выводы:
- если параметр α < pмакс./m, то выигрыша по времени при распознавании не будет;
- если параметр α = pмакс./m, то T0 расп. = = Tравн. расп.;
- если α > pмакс./m, то можно будет наблюдать уменьшение времени распознавания.
Дополнительно отметим, что с ростом α время распознавания тоже будет уменьшаться, но только до своей нижней границы:
 .
.
 Рассмотрим достоинства и недостатки данной реализации функции P(m, n). Среди достоинств можно выделить простоту реализации функции P(m, n), отсутствие трудоемких вычислений и то, что заранее известно, какие объекты на какие компьютеры попадут.
Рассмотрим достоинства и недостатки данной реализации функции P(m, n). Среди достоинств можно выделить простоту реализации функции P(m, n), отсутствие трудоемких вычислений и то, что заранее известно, какие объекты на какие компьютеры попадут.
Главным недостатком данной функции P(m, n) является то, что она не учитывает особенности скорости обработки компьютерами объектов. Другими словами, у компьютеров может быть разная производительность, а время работы вычислительной системы n компьютеров определяется временем работы самым медленным K1 мин. произ. компьютером. Отсюда вытекает возможность простоя вычислительных ресурсов других компьютеров.
Одним из способов решения проблемы простоя компьютеров является возврат системе компьютера, который выполнил свою работу, чтобы он мог выполнять работу уже другой задачи. Определить объем работы (количество объектов для распознавания) компьютера возможно благодаря тому, что заранее известно распределение объектов по компьютерам.
Но этот способ не поможет решить проблему, если задачу нужно решить в минимальные сроки, то есть критерием оптимальности выступит время распознавания. Несмотря на наличие свободных ресурсов, система не сможет ими воспользоваться для сокращения времени распознавания объектов.
Второй вариант. В предыдущем примере существует проблема простоя компьютеров. Для ее решения можно предложить реализацию функции P(m, n) на основе жадного алгоритма, суть которого заключается в том, чтобы отправлять объект для распознавания первому освободившемуся компьютеру, тем самым уменьшая время простоя.
Введем следующие параметры: число b – число классифицируемых объектов, которое пришло на вход K1 мин. произ. компьютера; число z = pмакс. – b – число перераспределенных объектов, то есть, ес- ли на вход K1 мин. произ. компьютера поступит число b и b < pмакс., то жадный алгоритм перераспреде- лит z объектов с K1 мин. произ. компьютера на другие компьютеры, тем самым уменьшая время их простоя.
В результате работы этого алгоритма могут сло- житься две различные ситуации.
1. Жадному алгоритму не удалось переопределить число объектов, пришедших на вход K1 мин. произ. компьютера, то есть b = pмакс. Тогда Tжадн. расп. = Tравн. расп. и нет никакого выигрыша во времени. Такая ситуация возможна, когда скорости Vi средн. опред. всех n компьютеров равны между собой. В таком случае распределение классифицируемых объектов между n компьютерами жадного алгоритма будет совпадать с распределением равномерного алгоритма.
2. Жадному алгоритму удалось переопределить число объектов, пришедших на вход K1 мин. произ. компьютера, то есть b < pмакс. Тогда Tжадн. расп. < < Tравн. расп.. Для доказательства обратимся к рисунку 4.
Рассмотрим точку времени Tb – время, когда завершит свою работу K1 мин. произ. компьютер по распознаванию b объектов. Стоит заметить, что в это время уже не будет объектов для распознавания. Иначе жадный алгоритм должен будет назначить K1 мин. произ. компьютеру объект для распознавания, что противоречит тому, что на вход K1 мин. произ. компьютера было подано только b объектов.
В точке времени Tb возможны два варианта работы жадного алгоритма.
1. Все остальные (n–1) компьютеры уже выполнили свою работу, то есть простаивают. Тогда время распознавания равно времени обработки K1 мин. произ. компьютером b объектов:
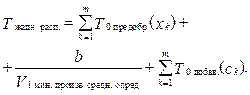 (11)
(11)
2. Часть компьютеров из n–1 еще обрабатывают свои последние объекты. Определим компьютер с минимальной производительностью среди n–1 компьютеров, то есть компьютер K2 мин. произ.. Для простоты сдвинем время начала обработки пос- леднего объекта K2 мин. произ. компьютера с точки T2 мин. произ. до точки Tb, то есть Tb = T2 мин. произ. + ∆T. Тогда время распознавания равно сумме времени обработки K1 мин. произ. компьютером b объектов и времени обработки K2 мин. произ. своего последнего объекта:
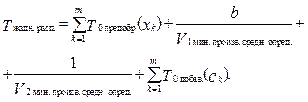 (12)
(12)
Очевидно, что время распознавания по формуле (12) больше времени распознавания по формуле (11). Поэтому дальше будем ориентироваться на время, рассчитанное по формуле (12).
Докажем теперь, что время распознавания по формуле (12) меньше времени распознавания по формуле (9). Очевидно, что можно опустить слагаемые 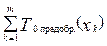 и
и  , так как они вносят одинаковый вклад в обе формулы. Для доказательства рассмотрим граничный случай, когда количество объектов в обеих формулах одинаково, то есть жадный алгоритм смог переопределить только один объект с компьютера K1 мин. произ.. Тогда формула (12) будет выглядеть следующим образом:
, так как они вносят одинаковый вклад в обе формулы. Для доказательства рассмотрим граничный случай, когда количество объектов в обеих формулах одинаково, то есть жадный алгоритм смог переопределить только один объект с компьютера K1 мин. произ.. Тогда формула (12) будет выглядеть следующим образом:
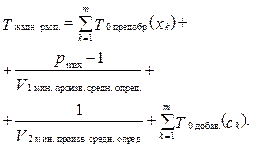 (13)
(13)
Проведя анализ формул (9) и (13), можно сделать вывод: для доказательства того, что Tжадн. расп.< < Tравн. расп., стоит сравнить между собой 1/V1 мин. произ. средн. опред. и 1/V2 мин. произ. средн. опред.. Как отмечалось выше, V1 мин. произ. средн. опред. ≥ ≥ V2 мин. произ. средн. опред. и Tb = T2 мин. произ.+ ∆T. Это позволяет сделать вывод, что 1/V1 мин. произ. средн. опред. > > 1/V2 мин. произ. средн. опред.. Знак «строго» берется потому, что даже при равенстве скоростей между собой необходимо учитывать тот факт, что Tb = = T2 мин. произ. + ∆T, то есть K2 мин. произ. компьютер начнет работу раньше, чем закончит работу K1 мин. произ. компьютер.
В других же случаях с уменьшением параметра b будет уменьшаться b/V1 мин. произ. средн. опред., что приводит к уменьшению времени распознавания.
Рассмотрим достоинства и недостатки реализации функции P(m, n) в виде жадного алгоритма. Среди достоинств можно выделить простоту реализации функции P(m, n), отсутствие трудоемких вычислений и возможность уменьшения времени простоя компьютеров, что отразится на времени распознавании.
Недостатки данной функции P(m, n): не- известно, какие объекты на какие компьютеры попадут; распределение по жадному алгоритму не всегда будет оптимальным, если критерием оптимальности выступит общее время распознавания.
Характеристики сети. Важнейшей характеристикой системы является время коммутации и передачи данных по каналам связи в сети, которое может оказать значительное влияние на длительность решения задачи. Фактически интерес представляет время, через которое после начала процесса вычисления пользователь получит его результат. Время получения результата на i-м компьютере (Ti получ. резул.) складывается из времени подключения (Ti подкл.) и времени на обработку данных (Ti обраб. дан.): Ti получ. резул. = Ti подкл. + Ti обраб. дан..
 Рассчитаем время, которое нужно потратить на этап обучения (рис. 5).
Рассчитаем время, которое нужно потратить на этап обучения (рис. 5).
Суть обучения n компьютеров заключается в следующем: пользователь передает на сервер файл с обучающими объектами; сервер отправляет дальше этот файл параллельно n компьютерам; каждый компьютер обучается на этом файле. Время обучения n компьютеров рассчитывается следующим образом:
 , (14)
, (14)
где Tзагр.(Fобуч.) – время загрузки файла Fобуч. на сервер; Tмакс. перед. – максимальное время передачи файла Fобуч. на один из n компьютеров; Tмакс. обуч. – максимальное время обучения одного из n компьютеров на основе файла Fобуч.
 Рассчитаем время, необходимое на распознавание (рис. 6).
Рассчитаем время, необходимое на распознавание (рис. 6).
Распознавание происходит следующим образом: 1) пользователь передает на сервер файл с классифицируемыми объектами; 2) сервер осуществляет предобработку и распределение классифицируемых объектов из этого файла параллельно n компьютерам согласно реализации функции P(m, n); 3) i-й компьютер, получив классифицируемый объект, начинает процесс определения его класса; 4) класс распознанного объекта записывается в выходной файл i-го компьютера, после чего отправляется на сервер; 5) сервер после получения класса объекта начинает добавление его в общий выходной файл; 6) после добавления всех классов в общий выходной файл сервер отправляет общий выходной файл клиенту.
Как уже отмечалось, общее время работы системы зависит от времени работы звена с максимальным временем обработки своих объектов, то есть компьютером Kдолг. звена. Для равномерного распределения компьютер Kдолг. звена определялся параметром V1 мин. произ. средн. опред., но при этом не учитывались характеристики канала связи. Поэтому теперь для Ki-го компьютера время расчета определения класса одного объекта складывается из следующих параметров: Ti сетев. опред. = Ti перед.(xk) + + Ti сред. опред. (xk) + Ti перед. (ck), где Ti перед. (xk) – время передачи xk-го объекта с сервера на i-й компьютер; Ti сред. опред. (xk) – время определения класса xk-го объекта на i-м компьютере; Ti перед. (ck) – время передачи класса xk-го объекта с i-го компьютера на сервер.
Другими словами, компьютер Kдолг. звена будет определяться не только производительностью компьютера, но и характеристиками канала связи. Те- перь с учетом вышесказанных замечаний и формулы (7) рассчитаем общее время распознавания:
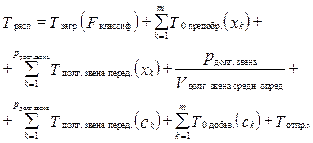 (15)
(15)
где Tзагр.(Fклассиф.) – время загрузки файла Fклассиф. на сервер;  – время передачи pдолг. звена объектов на компьютер Kдолг. звена;
– время передачи pдолг. звена объектов на компьютер Kдолг. звена;  – время передачи классов pдолг. звена объектов на сервер; Tотпр. – время отправки общего выходного файла клиенту.
– время передачи классов pдолг. звена объектов на сервер; Tотпр. – время отправки общего выходного файла клиенту.
Если время решения задачи T0 реш. зад. = T0 обуч. + + T0 расп. на K0 компьютере меньше времени Tпаралл. реш. зад. = Tпаралл. обуч. + Tпаралл. расп. (с учетом времени коммутации и передачи данных по сети), то распараллеливание не повысит общую производительность системы. Здесь T0 обуч. рассчитывается по формуле (1), T0 расп. – по формуле (3), Tпаралл. обуч. – по формуле (14), Tпаралл. расп. – по формуле (15). Такая ситуация может возникнуть при значительном влиянии характеристик канала связи, в том числе времени коммутации и передачи данных.
Минимизировать Ti обраб. дан. можно за счет установки высокопроизводительного оборудования. Минимизация Tрасп. достигается путем установки дополнительных компьютеров, тем самым снижая среднее значение Ti обраб. дан., а также стремлением к максимально низкому значению Ti подкл., размещая сервер и компьютеры в одной локальной сети. Следует помнить, что при Ti обраб. дан., близком к Ti подкл., требуется решить задачу выбора оптимального количества компьютеров, дабы избежать отрицательного эффекта от применения системы. Оптимизировать параметры Ti подкл. и Ti обраб. дан. стоит исходя из соображений целесообразности и общей эффективности.
В ходе исследования было разработано web-ориентированное инструментальное средство по распознаванию образов в идее расширяемой библиотеки методов на основе прецедентов, способное не только работать на одном сервере, но и распараллеливать обработку данных между компьютерами.
Реализация такой параллельности была представлена в статье [12], где описаны теоретические и экспериментальные разработки двух схем распараллеливания на основе grid-технологий: с распараллеливанием алгоритма обучения и с распараллеливанием алгоритма распознавания, а также представлены элементы практических наработок различных этапов параллельного распознавания на n компьютерах на основе метода k ближайших со- седей.
Перспективность исследования определяется практической эффективностью разработанного web-приложения. Практика показывает, что распараллеливание позволяет эффективно применять вычислительные ресурсы для решения задач в минимальные сроки, а применение web-технологии – повысить объем обрабатываемых данных и скорость доступа к ним.
Теоретические выкладки и расчеты работы являются базовыми для практических разработок данного web-приложения. В статье обозначены ограничения на применение вычислительных ресурсов, несоблюдение которых приводит к ухудшению результатов времени распознавания. Также рассчитана минимальная граница времени распознавания вне зависимости от количества используемых компьютеров.
Реализуемая архитектура инструментария позволяет решать задачу повышения эффективности вычислительных ресурсов через процедуры настройки структуры подключаемых методов и алгоритмов обработки данных и реконфигурирования подключаемых технических вычислительных средств Internet-сети.
Литература
1. Козлов А.Н. Интеллектуальные информационные системы. Пермь: Изд-во Перм. ГСХА, 2013. 278 с.
2. Громов Ю.Ю., Иванова О.Г., Алексеев В.В. [и др.]. Интеллектуальные информационные системы и технологии. Тамбов: Изд-во ТГТУ, 2013. 244 с.
3. Han J., Kamber M., Pei J. Data mining: concepts and techniques, Elsevier, 2012, 744 p.
4. Фомин Я.А. Распознавание образов: теория и применения. М.: Фазис, 2014. 460 c.
5. Мерков А.Б. Распознавание образов: введение в методы статистического обучения. М.: Едиториал УРСС, 2011. 254 с.
6. Sandoval J., Hernández G. Learning of natural trading strategies on foreign exchange high-frequency market data using dynamic bayesian networks. Machine Learning and Data Mining in Pattern Recognition. Proc. 10th Intern. Conf., 2014, pp. 408–421.
7. Сикулер Д.В., Фомин В.В. Проектные решения web-ресурса интеллектуального анализа данных и поддержки принятия решений на основе унифицированного класса методов решающих функций. СПб: Изд-во РГПУ, 2016. 102 с.
8. Марманис Х., Бабенко Д. Алгоритмы интеллектуального Интернета. Передовые методики сбора, анализа и обработки данных; [пер. с англ.]. СПб: Символ-Плюс, 2011. 466 с.
9. Варшавский П.Р., Еремеев А.П. Моделирование рассуждений на основе прецедентов в интеллектуальных системах поддержки принятия решений // Искусственный интеллект и принятие решений. 2009. № 1. С. 45–57.
10. Петров Е.В., Фомин В.В. Organization of parallel processing for implementation of web data mining system // Ученые записки РГГМУ. 2014. № 33. С. 149–154.
11. Алпатов А.Н. Развитие распределенных технологий и систем // Перспективы науки и образования. 2015. № 2. С. 60–66.
12. Фомин В.В., Александров И.В. Об одном опыте применения параллельных вычислений при разработке web-инструментария распознавания образов // Программные продукты, системы и алгоритмы. 2017. № 1. URL: http://swsys-web.ru/ experience-in-parallel-computing-web-tool-for-pattern-recognition. html (дата обращения: 02.04.2017).



 . (1)
. (1)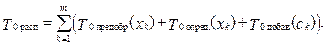 (2)
(2)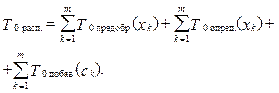 (3)
(3) .
. . (4)
. (4) (5)
(5) и передает его функции P(m, n); 2) функция P(m, n) распределяет полученный xk-й объект на Ki-й компьютер согласно алгоритму реализации функции P(m, n); 3) после распознавания на выходе Ki-го компьютера образуется результат в виде класса ck; 4) сервер, получив класс ck, добавляет его в выходной файл с помощью функции Fдобав.(ck).
и передает его функции P(m, n); 2) функция P(m, n) распределяет полученный xk-й объект на Ki-й компьютер согласно алгоритму реализации функции P(m, n); 3) после распознавания на выходе Ki-го компьютера образуется результат в виде класса ck; 4) сервер, получив класс ck, добавляет его в выходной файл с помощью функции Fдобав.(ck).
 (6)
(6) – сумма времени ожидания, пока все n–1 компьютеры не прочитают свои объекты, и времени чтения компьютером Kдолг. звена своего объекта;
– сумма времени ожидания, пока все n–1 компьютеры не прочитают свои объекты, и времени чтения компьютером Kдолг. звена своего объекта;  – время определения класса одного классифицируемого объекта компьютером Kдолг. звена;
– время определения класса одного классифицируемого объекта компьютером Kдолг. звена; 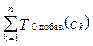 – сумма времени ожидания, пока все n–1 компьютеры не запишут свои классы, и времени записи компьютером Kдолг. звена класса своего объекта; p долг. звена – количество объектов, которое распознает компьютер Kдолг. звена.
– сумма времени ожидания, пока все n–1 компьютеры не запишут свои классы, и времени записи компьютером Kдолг. звена класса своего объекта; p долг. звена – количество объектов, которое распознает компьютер Kдолг. звена. (7)
(7) , (8)
, (8)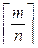 – округление числа m/n до целого числа в большую сторону.
– округление числа m/n до целого числа в большую сторону.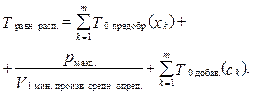 (9)
(9)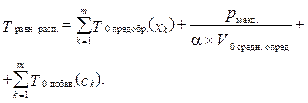 (10)
(10)
 всегда будет нижней границей времени распознавания.
всегда будет нижней границей времени распознавания.
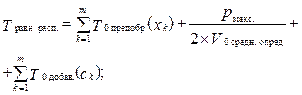
 .
.
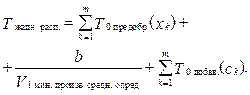 (11)
(11)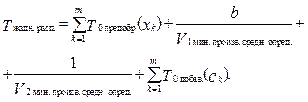 (12)
(12)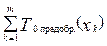 и
и  , так как они вносят одинаковый вклад в обе формулы. Для доказательства рассмотрим граничный случай, когда количество объектов в обеих формулах одинаково, то есть жадный алгоритм смог переопределить только один объект с компьютера K1 мин. произ.. Тогда формула (12) будет выглядеть следующим образом:
, так как они вносят одинаковый вклад в обе формулы. Для доказательства рассмотрим граничный случай, когда количество объектов в обеих формулах одинаково, то есть жадный алгоритм смог переопределить только один объект с компьютера K1 мин. произ.. Тогда формула (12) будет выглядеть следующим образом: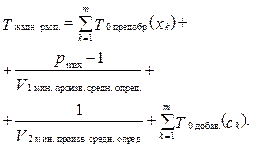 (13)
(13)
 , (14)
, (14)
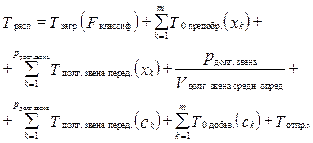 (15)
(15) – время передачи pдолг. звена объектов на компьютер Kдолг. звена;
– время передачи pдолг. звена объектов на компьютер Kдолг. звена;  – время передачи классов pдолг. звена объектов на сервер; Tотпр. – время отправки общего выходного файла клиенту.
– время передачи классов pдолг. звена объектов на сервер; Tотпр. – время отправки общего выходного файла клиенту.