Устойчивое функционирование распределенных информационных систем (РИС) является за- логом эффективной работы организаций и предприятий в различных сферах экономики. Под устойчивостью функционирования системы понимается ее способность выполнять возложенные функции с заданными показателями качества в условиях воздействия внутренних и внешних дестабилизирующих факторов.
В отличие от надежности под устойчивостью подразумевается обеспечение требуемых значений показателей эффективности системы в условиях возможной ее реконфигурации (изменения ее структуры).
В общем случае дестабилизирующие факторы в РИС делятся по местоположению источника на внешние и внутренние, а по характеру возникновения – на случайные и преднамеренные [1].
Наиболее опасными с точки зрения обеспечения целевых показателей функционирования РИС являются дестабилизирующие факторы, в результате воздействия которых ухудшаются параметры процессов обеспечения информационных запросов пользователей, хранения и обработки информации. К таким факторам можно отнести следующие:
- структурная деградация сети (выход из строя средств обработки информации в узлах распределенной системы, каналов передачи информации);
- разрушение элементов ПО (разрушение данных и кодов исполняемых программ, внесение тонких, труднообнаруживаемых изменений в информационные массивы);
- внедрение программных закладок в другие программы и подпрограммы (вирусный механизм воздействий);
- искажение или уничтожение собственной информации сервера и тем самым нарушение работы сети;
- нарушение целостности (преднамеренное или случайное искажение, разрушение) элементов информационного обеспечения (баз и банков данных), модификация пакетов сообщений и др.
Воздействие этих факторов может иметь катастрофические последствия вплоть до выхода из строя технического, программного и информационного обеспечения систем и, как следствие, привести к нарушениям в процессах обработки инфор- мации или к отказам функционирования систем в целом [1]. Для нейтрализации последствий воздействия дестабилизирующих факторов может потребоваться реструктуризация системы с перераспределением информационных ресурсов.
В качестве показателя устойчивости функционирования системы в условиях воздействия i-го дестабилизирующего фактора обычно понимается коэффициент устойчивости Кучi, определяемый из выражения Кучi=1– , где Ктр – требуемое значение показателя качества функционирования системы; Кдфi – значение показателя качества функционирования системы в условиях воздействия i-гo дестабилизирующего фактора [2, 3].
, где Ктр – требуемое значение показателя качества функционирования системы; Кдфi – значение показателя качества функционирования системы в условиях воздействия i-гo дестабилизирующего фактора [2, 3].
Тогда общий показатель устойчивости системы, выражаемый как коэффициент устойчивости Ку, определяется выражением Ку =  , где I – количество учитываемых дестабилизирующих факторов в системе.
, где I – количество учитываемых дестабилизирующих факторов в системе.
Кроме того, за показатели качества функционирования системы, характеризующие ее устойчивость, могут быть взяты время выполнения рассматриваемого процесса в системе, коэффициент готовности системы, коэффициент эффективности системы и другие [3].
В настоящее время наиболее эффективными для обеспечения устойчивости функционирования РИС являются следующие подходы:
- совершенствование процессов хранения и обработки информации (ПХОИ), в том числе в части обеспечения их устойчивости;
- создание высоконадежных подсистем хранения и обработки данных с учетом их резервирования [4].
Для повышения устойчивости ПХОИ на этапах проектирования и эксплуатации РИС целесообразно выполнять рациональное распределение элементов ПО и информационных массивов по узлам вычислительной сети, а при воздействии дестабилизирующих факторов, в случае структурной деградации сети – их перераспределение [4].
Основу РИС составляет система хранения и обработки данных (СХОД), предназначенная для организации надежного, а также отказоустойчивого хранения данных, высокопроизводительного доступа серверов к устройствам хранения и обработки информации. Обеспечение сохранности информации в СХОД производится путем применения специальных мер организации хранения, восстановления (регенерации) информации, специальных устройств резервирования. Качество обеспечения сохранности информации зависит от ее целостности (точности, полноты) и готовности к постоянному использованию [5–7].
Наиболее простые и эффективные способы обеспечения сохранности информации в СХОД – создание резервных хранилищ данных и реализация мероприятий по оперативному и восстановительному резервированию информации [7].
По типу устройств резервирования резервные хранилища информации в СХОД [5] делятся на хранилища на базе HDD/SSD-дисков (RAID-массивы), на магнитных лентах, на базе оптических дисков.
По количеству уровней резервирования резервные хранилища делятся на одноуровневые и многоуровневые.
При большом количестве разновидностей систем и средств высоконадежного хранения данных, а также их конфигураций стоит задача выбора их состава с учетом решаемых СХОД задач.
Решение задач организации ПХОИ позволяет повысить эффективность функционирования системы за счет снижения издержек, связанных с разрушением информации, включая потери от невозможности решения задач и получения недостоверных выходных результатов, за счет уменьшения времени и затрат на восстановление разрушенной или искаженной информации, рационального использования внешней памяти вычислительных средств для размещения данных РИС и т.д.
Для рациональной организации ПХОИ в РИС в структуре СХОД создают центры хранения и обработки информации (ЦХОИ), основной задачей которых является реализация эффективных с точки зрения решаемых в системе задач ПХОИ.
Для обеспечения сохранности информации целесообразно в ЦХОИ создавать подсистемы хранения и обработки данных, основу которых составляют технические средства хранения и обработки информации, интегрируемые в ЦХОИ. В качестве элементов ПО рассматривались программные комплексы, программные модули, осуществляющие решение функциональных задач с использованием информационных массивов в РИС.
Вследствие ограниченности материальных средств, выделяемых на создание РИС, хранение и обработка информации в них осуществляются в ограниченном количестве ЦХОИ, создаваемых в соответствующих узлах сети. В этих центрах аккумулируются мощные вычислительные средства и средства хранения данных, обеспечивающие решение функциональных задач как отдельного сегмента сети, так и системы в целом.
Таким образом, для обеспечения устойчивости функционирования РИС разработан комплекс математических моделей оптимизации
- распределения элементов ПО функциональных задач по узлам сети по критерию минимума объема информации, передаваемой по каналам связи при решении всех функциональных задач;
- распределения информационных ресурсов по ЦХОД по критерию минимума общего значения среднего времени восстановления информации в СХОД;
- состава технических средств СХОД по критерию максимума значения коэффициента готовности системы хранения данных в целом;
- распределения резерва информационных ресурсов по ЦХОД по критерию минимума среднего времени решения всех задач в РИС [8].
Данные задачи относятся к классу задач комбинаторной оптимизации [9], а именно целочисленного дискретного программирования с булевыми переменными [9, 10].
В общем случае математические модели обеспечения устойчивости функционирования РИС могут быть следующими [11].
Определить такие значения xj (j=1, 2, …, N), что
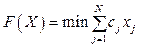 (1)
(1)
при ограничениях
xj = {0, 1}, j = 1, 2, …, N; (2)
 i = 1, 2, …, M, (3)
i = 1, 2, …, M, (3)
где N – число переменных; M – число ограничений.
Для обеспечения эффективности практического применения разработанных математических моделей к методам их решения должны предъявляться определенные требования:
- возможность получения оптимального (квазиоптимального) решения в минимально возможное время;
- возможность управления точностью полученного решения в условиях ограничения на время решения задач;
- невысокая вычислительная сложность;
- возможность распараллеливания процесса получения оптимального (квазиоптимального) решения;
- простота программной реализации вычислительных процедур алгоритма;
- возможность практического применения на вычислительных комплексах с ограниченными характеристиками (невысокой производительности).
Для получения точного решения задачи (1)–(3) существует достаточно большое количество методов дискретной оптимизации [9, 10], наиболее распространенным и наиболее широко используемым из которых является метод ветвей и границ [10].
Основными процедурами, составляющими метод ветвей и границ, являются построение дерева возможных вариантов решения, определение оценки границы решения для каждой вершины дерева и отсечение бесперспективных вершин, которые не могут привести к улучшению рекорда [10].
Общая эффективность метода ветвей и границ при решении задач обеспечения устойчивости функционирования РИС непосредственно зависит от выбора стратегии ветвления переменных и способа оценки границ решения, а также от способа организации компьютерных вычислений [10, 12]. Результаты этого выбора зависят от конкретных условий решения данных задач оптимизации.
Для формирования дерева вариантов в ходе решения задачи наиболее широко используют такие стратегии ветвления переменных [12], как фланговая (левофланговая, правофланговая), фронтальная, локально-избирательная и глобально-поисковая.
Выбор стратегии ветвления оказывает влияние на требуемый для хранения дерева вариантов при решении задачи объем оперативной памяти вычислительного комплекса, а также (за счет особенностей реализации поисковых процедур на дереве решений) на время решения.
Эффективность вычислительных алгоритмов зависит от точности и простоты способа определения верхней или нижней границы возможных решений [10, 12]. Точность определения верхней (нижней) границы целевых решений напрямую влияет на число бесперспективных вариантов, которые отсеиваются в процессе решения. Увеличение точности расчета границ решений связано с ростом вычислительной сложности алгоритмов и, как следствие, – объема вычислений.
В качестве методов оценки границ решения используют точные методы (симплекс-метод и его модификации) и приближенные методы решения двойственной задачи.
Применение теории двойственности при решении задач методом ветвей и границ позволяет использовать для оценки границы решения приближенные алгоритмы [10]. Однако этот способ оценки границы решения эффективен только при простом и достаточно точном алгоритме решения двойственной задачи.
При решении задачи (1)–(3) методом ветвей и границ условие целочисленности переменных (2) можно заменить условием
0 ≤ xj ≤ 1. (4)
Двойственной задачей по отношению к (1), (2), (4) является задача
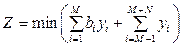 (5)
(5)
при ограничениях
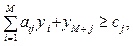 j = 1, 2, …, N, (6)
j = 1, 2, …, N, (6)
yi ³ 0, i = 1, 2, …, M+N. (7)
В работе [6] предложен приближенный алгоритм оценки границ решения в методе ветвей и границ, основанный на градиентной процедуре решения задачи, двойственной по отношению к исходной. В данном алгоритме использование свойств двойственной задачи и особенностей реализации градиентной процедуры позволяет в процессе решения осуществлять оценку вклада каждой переменной в результат и за счет этого определять порядок ветвления переменных. Для повышения эффективности метода ветвей и границ предложено однократное решение задачи, двойственной по отношению к исходной, с применением данного ал- горитма для определения порядка ветвления переменных [10, 13].
Экспериментальная оценка эффективности методов решения задач обеспечения устойчивости функционирования РИС проводилась на вычислительной системе со следующими характеристиками: OC Windows 7 Professional x64 Service Pack 1; процессор Intel Core i5-3450 c тактовой частотой 3.10 Ghz; объем оперативной памяти 8 Gb.
При экспериментальной проверке методов и алгоритмов решения задач обеспечения устойчивости функционирования РИС методом ветвей и границ ставились следующие задачи:
- оценка эффективности стратегий ветвления переменных в методе ветвей и границ;
- оценка эффективности применения предложенного способа сокращения времени решения задач методом ветвей и границ на основе применения теории двойственности;
- определение параметров генетического алгоритма (ГА), обеспечивающих наилучшее качество получаемого решения;
- определение влияния исходных данных на эффективность методов;
- определение области эффективного применения методов решения формализованных математических моделей.
Исходные данные для экспериментальной проверки эффективности методов решения разработанных математических моделей формировались следующим образом.
Коэффициенты при переменных в целевой функции и ограничениях генерировались как независимые друг от друга целые случайные числа, равномерно распределенные на интервале [0, 100]. Правые части ограничений вычислялись по зависимости 
Коэффициент Q определял жесткость ограничений и выбирался из интервала [30, 90] с шагом 20 %. Для каждой размерности решалось по 10 задач.
В качестве характеристик метода ветвей и границ [14, 15] использовались следующие величины: время решения задачи (tmin – минимальное, tmax – максимальное, tср – среднее); число просмотренных вершин (Vmin – минимальное, Vmax – максимальное, Vcp – среднее); общее время определения границ решения выбранным методом (Tmin – минимальное, Tmax – максимальное, Tcp – среднее).
Для оценки эффективности метода ветвей и границ при решении разработанных задач использовался разработанный программный комплекс [16].
Результаты экспериментальной оценки эффективности применения метода ветвей и границ для решения задач различных размерностей приведены на рисунках 1–4.




Из представленных данных видно, что наимень- шее время решения задач обеспечивают глобально-поисковая и локально-избирательная стратегии ветвления. Наименее эффективной является фланговая стратегия ветвления. Следует отметить нестабильность поведения фронтальной стратегии ветвления.
При некоторых условиях использование фронтальной стратегии приводит к тому, что процесс решения задачи сводится к полному перебору вариантов решения. Поведение фронтальной стратегии ветвления не зависит от исходных данных решаемых задач и выбора метода оценки границ решения.
Результаты оценки влияния жесткости ограничений на эффективность стратегий ветвления пред- ставлены на рисунках 2 и 3. На них видно, что со снижением жесткости ограничений число просмотренных вершин и, соответственно, время решения задач уменьшаются. Это влияние особенно сильно проявляется с увеличением размерности задачи (числа переменных). Так, на размерности 100 переменных и 30 ограничений снижение жесткости ограничений с Q = 50 % до Q = 90 % сокращает время решения задач в 29 раз. Это объясняется снижением количества перспективных вершин среди не ответвленных на дереве решений. Таким образом, повышение жесткости ограничений приводит к значительному увеличению числа просматриваемых методом вариантов решения, что ставит под сомнение целесообразность использования в этих случаях таких стратегий ветвления переменных, как фланговая, фронтальная и их модификации.
Анализ результатов расчетов, представленных на рисунке 3, показывает, что в зависимости от выбранной стратегии ветвления 27–89 % от времени решения задачи составляет совокупное время определения границ решения симплекс-методом.
При оценке влияния применения алгоритма определения порядка ветвления переменных на эффективность метода ветвей и границ в качестве методов оценки границ решения использовались симплекс-метод и приближенный метод решения двойственной задачи.
Результаты экспериментальной проверки эффективности влияния предварительного определения порядка ветвления переменных приведены в таблице 1 и на рисунке 4 [13–15]. В качестве методов оценки границ решения использовались симплекс-метод и рассмотренный выше приближенный метод решения двойственной задачи на основе применения градиентной процедуры, в качестве стратегии ветвления переменных – глобально-поисковая стратегия.
 Из таблицы 1 и рисунка 4 видно, что предварительное определение порядка ветвления переменных при решении задач различных размерностей позволяет снизить время решения задач в 3–14 раз. Результаты решения стабильны независимо от способа оценки верхней границы. Это говорит об эффективности предложенного алгоритма и целесообразности его использования при решении практических задач методом ветвей и границ.
Из таблицы 1 и рисунка 4 видно, что предварительное определение порядка ветвления переменных при решении задач различных размерностей позволяет снизить время решения задач в 3–14 раз. Результаты решения стабильны независимо от способа оценки верхней границы. Это говорит об эффективности предложенного алгоритма и целесообразности его использования при решении практических задач методом ветвей и границ.
Таким образом, экспериментальная проверка эффективности метода ветвей и границ показала, что наиболее эффективными при решении задач обеспечения устойчивости РИС являются глобально-поисковая и локально-избирательная стратегии ветвления переменных. Увеличение жесткости ограничений приводит к значительному росту времени решения задач методом ветвей и границ независимо от используемых стратегий ветвления и методов оценки границ решения. Применение предложенного способа ранжирования переменных по уровню влияния на результат решения задачи для организации процесса ветвления переменных совместно с точным методом оценки границ решения обеспечивает существенное (от 3 до 14 раз) повышение производительности метода ветвей и границ.
Достоинством метода ветвей и границ является точность получаемого решения за ограниченное время, недостатком – экспоненциальная зависимость времени решения от размерности решаемых задач [15].
Для практического применения формализованных задач обеспечения устойчивости функционирования РИС решения задачи в условиях жестких ограничений на время решения предложено и экспериментально проверено использование ГА как варианта стохастического эволюционного поиска решения. Основу ГА составляет хромосома (особь) [17, 18].
Применительно к данной задаче хромосома (особь) состоит из набора N генов, каждый из которых представляет собой значение соответствующей переменной решаемой задачи и принимает значение 0 или 1.
В ГА над хромосомами выполняются следующие действия: определение значения функции приспособленности, скрещивание (кроссинговер), мутация, отбор особей для скрещивания.
Значение функции приспособленности используется для оценки качества варианта решения, соответствующего значениям генов хромосомы.
Функция приспособленности рассчитывается как значение целевой функции.
Если геном хромосомы соответствует недопустимому значению переменных (не выполняются ограничения), функция приспособленности возвращает значение < 0 (например –100 000), в противном случае – положительное число, значение W.
Для генерации новых вариантов решения (особей) в ГА используют механизмы отбора особей, скрещивания и мутации хромосом.
Для работы ГА [17–19] обычно используют следующие популяции:
- исходная популяция; служит для хранения особей, участвующих в текущем шаге ГА; на начальном шаге ГА исходная популяция обычно генерируется случайным образом;
- родительская популяция (родительский пул); в родительскую популяцию отбираются все особи исходной популяции, значения функции приспособленности которых не меньше среднего значения функции приспособленности для исходной популяции в целом;
- элитная популяция; служит для сохранения лучших особей родительской (исходной) популяции;
- дочерняя популяция; формируется путем многократного выполнения операций отбора особей, кроссинговера, мутации; на основе дочерней популяции формируется исходная популяция для следующего шага ГА.
Для упрощения процедур ГА предлагается использовать исходную популяцию постоянного размера. В случае, если на какой-либо итерации вновь сформированная популяция, которая на следующей итерации будет использоваться как исходная, имеет размер, менее заданного, предлагается дополнять ее до требуемого размера случайно сгенерированными особями.
Особи для скрещивания выбираются из родительской популяции. Первая хромосома выбирается случайным образом.
Выбор второй особи для скрещивания возможен по следующим вариантам:
- случайный выбор; вторая особь выбирается случайно из родительской популяции; данный вариант наиболее прост для реализации, однако вследствие своей природы не может гарантировать качество получаемого решения;
- родственное скрещивание на основе анализа расстояния между особями; в качестве расстояния между хромосомами для решаемой задачи целесообразно использовать расстояние Хэмминга, определяемое для двух особей как  , где g1i и g2i – значения i-х генов 1-й и 2-й особей.
, где g1i и g2i – значения i-х генов 1-й и 2-й особей.
В соответствии с этим различают близкородственное (инбридинг) и дальнеродственное (аутбридинг) скрещивание.
Аутбридинг – выбирается хромосома с максимальным значением расстояния Хэмминга до первой выбранной: S®max. Данный вид отбора обеспечивает снижение скорости сходимости алгоритма к локальному экстремуму и увеличивает вероятность достижения глобального экстремума.
Инбридинг – выбирается хромосома с минимальным расстоянием от выбранной первой: S®min. Данный вид отбора обеспечивает максимально быструю сходимость алгоритма к локальному экстремуму.
Для обеспечения сохранения лучших найден- ных особей содержимое элитной популяции авто- матически включается в дочернюю популяцию на текущем шаге алгоритма.
Размер элитной популяции Lel определяется как Lel = kel Lsr, где kel – коэффициент элитизма; Lsr – размер исходной популяции.
Операция скрещивания (кроссинговер) выполняется над парой хромосом, являющихся родительскими. Результат операции – две хромосомы-потомка.
Исследования показали, что одним из наиболее эффективных с точки зрения конечного результата является универсальный кроссинговер, который выполняется следующим образом.
Генерируется шаблон двоичных чисел длиной N. Шаблон указывает, какие гены должны наследоваться от первого родителя (остальные гены берутся от второго родителя).
Для первого потомка: если в j-й позиции шаблона 1, то j-й ген для данного потомка берется от первого родителя, если 0 – от второго. Для второго потомка: если в j-й позиции шаблона 1, то j-й ген для данного потомка берется от второго родителя, а если 0 – от первого.
Кроме того, потенциально хороший результат может показать триадный кроссинговер с формированием маски кроссинговера из лучшей особи элитной популяции. Он аналогичен универсальному, за исключением того, что маска кроссинговера формируется не случайно, а соответствует лучшей особи в элитной популяции.
В качестве претендента на использование возможно применение триадного кроссинговера на основе анализа схемы [20] в следующем виде.
Пусть g1, g2 и g3 – родительские хромосомы; 
 ,
,  – значения функции приспособленности родительских особей. g1 и g2 выбираются в соответствии с текущей схемой отбора особей, g3 – случайным образом из особей родительской популяции.
– значения функции приспособленности родительских особей. g1 и g2 выбираются в соответствии с текущей схемой отбора особей, g3 – случайным образом из особей родительской популяции.
Так как гены принимают только значения из набора {0, 1}, обозначим через P0(j) и P1(j) частоты появления значений 0 и 1 для j-го гена в родительской популяции соответственно. Тогда для всех j, j=1, 2, …, N, определим значения генов дочерних особей  и
и  по следующим правилам.
по следующим правилам.
Если 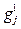 =
= 
 , то
, то  =
= 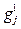 .
.
Если 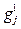 ¹
¹  , то
, то
при 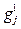 = 0, если
= 0, если  P0(j) ³
P0(j) ³ P1(j),
P1(j),  =
= 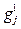 и
и  =
=  в противном случае;
в противном случае;
при 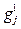 = 1, если
= 1, если  P1(j) ³
P1(j) ³ P0(j),
P0(j),  =
= 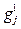 и
и  =
=  в противном случае.
в противном случае.
Если  >
> , то g4 = g1,
, то g4 = g1,  =
= и g4 = g2,
и g4 = g2,  =
= в противном случае.
в противном случае.
Если 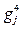 =
=  , то
, то  =
= 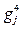 .
.
Если 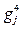 ¹
¹  , то
, то
при 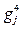 = 0, если
= 0, если  P0(j) ³
P0(j) ³ P1(j),
P1(j),  =
= 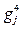 и
и  =
=  в противном случае;
в противном случае;
при  , если
, если  P1(j) ³
P1(j) ³ P0(j),
P0(j),  =
= 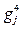 и
и  =
=  в противном случае.
в противном случае.
Нетрудно заметить, что при P1(j) = 1 или P0(j) = 1 все особи в популяции имеют одинаковое значение j-го гена и это значение гарантированно перейдет по наследству потомкам.
Операция мутации выполняется над выбранной хромосомой. Данный оператор необходим для «выбивания» популяции из локального экстремума и препятствует преждевременной сходимости. Это достигается за счет того, что изменяется случайно выбранный ген gi (i = 1, 2, ..., N) в хромосоме. Значение выбранного гена (переменной исходной задачи в данном варианте решения) инвертируется.
Введем обозначения: Ngen – число поколений, формируемых островом в одной итерации ГА; Pc – вероятность выполнения скрещивания хромосом; Pm – вероятность мутации хромосомы.
Простой ГА состоит из следующих шагов.
1. Начальная инициализация исходной популяции случайно сформированными хромосомами.
2. k = 0.
3. Определение среднего значения функции принадлежности хромосом исходной популяции.
4. Формирование родительской популяции из особей исходной популяции, значение функции принадлежности которых не меньше среднего значения функции принадлежности в исходной популяции. Определение длины родительской популяции Lpr.
5. Формирование элитной популяции из Lel лучших особей исходной популяции.
6. Включение в дочернюю популяцию хромосом, входящих в элитную популяцию.
7. i = 0.
8. Случайный выбор хромосомы g1 из родительской популяции.
9. В соответствии с заданным способом выбора второй хромосомы для скрещивания выбор из родительской популяции хромосомы g2.
10. Формирование случайного числа rnd Î Î [0, 1]. Если rnd ≤ Pc, выполнение процедуры скрещивания хромосом g1 и g2 c получением новых хромосом  и
и  , для которых выполняется расчет значения функции принадлежности. Если rnd > Pc, присвоение
, для которых выполняется расчет значения функции принадлежности. Если rnd > Pc, присвоение  значения g1 и
значения g1 и  значения g2.
значения g2.
11. Формирование случайных чисел из интервала [0, 1] rnd1 и rnd2. Если rnd1 ≤ Pm, выполнение операции мутации с хромосомой  Если rnd2 ≤Pm, выполнение операции мутации с хромосомой
Если rnd2 ≤Pm, выполнение операции мутации с хромосомой  .
.
12. Включение с учетом результатов проверки на совпадение хромосом и допустимость значения функции принадлежности хромосом  и
и  в до- чернюю популяцию.
в до- чернюю популяцию.
13. i = i+1.
14. Если i < Lpr/2, переход к шагу 8, в противном случае – к шагу 15.
15. Дополнение дочерней популяции хромосомами из родительской популяции, не входящими в состав дочерней. Определение размера дочерней популяции Lch.
16. Если Lch < Lsr, дополнение дочерней популяции случайно сформированными хромосомами в количестве Lsr – Lch.
17. Очистка исходной, родительской и элитной популяций. Перенос хромосом из дочерней популяции в исходную. Очистка дочерней популяции.
18. k = k + 1.
19. Если k < Ngen, переход к шагу 3, иначе – к шагу 20.
20. Формирование элитной популяции.
21. Конец. Результат – лучшая особь в элитной популяции.
При решении задач обеспечения устойчивости функционирования РИС рассматривались две схемы генерации особей для формирования исходных популяций:
- случайная генерация варианта решения (особи) с последующей проверкой на выполнимость ограничений;
- последовательная генерация варианта решения (особи) с поэтапной проверкой выполнимости ограничений.
Обе схемы основаны на случайной генерации значений переменных при решении задач обеспечения устойчивости функционирования РИС.
Первая схема потенциально имеет больше шансов сформировать оптимальное решение уже в начальной популяции, однако требует существенного отсева вариантов, не удовлетворяющих ограничениям.
В соответствии со второй схемой, если на последующем этапе полученные значения переменных в варианте решения задач обеспечения устойчивости функционирования РИС не удовлетворяют ограничениям, за вариант решения берется особь, полученная на предыдущем этапе. Данная схема формирует исходную популяцию за количество шагов, незначительно превышающее размер популяции.
Экспериментальная проверка показала, что реализация первой схемы занимает до 30 % от общего времени решения задачи. Причем с ростом размерности задачи, количества ограничений, жесткости ограничений эта доля времени существенно возрастает.
Применение второй схемы позволяет сократить долю времени на формирование исходной популяции до 1–2 % от общего времени решения. Причем при ужесточении или росте числа ограничений данная величина растет незначительно.
Таким образом, при решении практических за- дач целесообразно применять схему последова- тельного формирования вариантов решения (особей) при создании исходной популяции.
Определено, что наилучшие показатели при решении задач обеспечения устойчивости функционирования РИС простой ГА имеет при Pc = 0,8, Pm = 0,1, kel = 0,1.
Выбор схемы репродукции оказывает существенное влияние на качество получаемого результата. Однако эффективность схемы репродукции существенно зависит от результатов начальной инициализации исходной популяции. Неверный выбор схемы репродукции обычно приводит к существенному ухудшению качества получаемого решения. В связи с тем, что инициализация исходной популяции осуществляется случайным образом, заранее осуществить эффективный выбор схемы репродукции не представляется возможным. Поэтому предлагается использовать адаптивную схему репродукции. Для этого в каждую хромосому необходимо включить числовые метки используемых для ее получения схемы отбора и варианта кроссинговера.
На каждом шаге алгоритма (при формировании нового поколения особей) необходимо определить количество особей в родительской популяции, сформированных с использованием каждой схемы отбора и каждого вида кроссинговера, и рассчитать частоту (вероятность) использования схем отбора и вариантов кроссинговера.
При начальной инициализации исходной по- пуляции для всех хромосом данным меткам присваивается значение –1, а частоты применения схем отбора и вариантов кроссинговера принимают равновероятными. При этом схемы отбора особей и варианты кроссинговера используются случайным образом в соответствии с полученными частотами (вероятностями) их применения.
Для реализации адаптивной схемы репродукции рассматривались схемы отбора особей: аутбридинг, инбридинг, случайный отбор, а также варианты кроссинговера: одноточечный, двухточечный, универсальный, триадный (с формированием маски кроссинговера из лучшей особи элитной популяции), триадный с учетом схемы.
В связи с незначительным влиянием мутации особей на качество получаемого решения использовался только один вариант мутации – одноточечная мутация.
Экспериментальная проверка эффективности ГА осуществлялась с применением разработанной программы [21]. Результаты экспериментальной проверки представлены в таблицах 2, 3 и на рисунке 5.

Из таблиц 2 и 3 видно, что качество получаемого решения при использовании простого ГА вследствие сходимости к случайному локальному экстремуму может существенно варьироваться в зависимости от результата начальной инициализации исходной популяции [22].
Таблица 2
Время формирования 1-го поколения ГА (сек.)
Table 2
Time of formation of the 1st generation of GA (sec.)
|
Размерность задачи
|
Схема отбора особей
|
|
Аутбридинг
|
Инбридинг
|
Случайный
|
Адаптивный
|
|
70´4
|
0,00207
|
0,00205
|
0,00207
|
0,00208
|
|
100´4
|
0,00376
|
0,00376
|
0,00371
|
0,00375
|
|
150´4
|
0,008745
|
0,008761
|
0,008381
|
0,008636
|
Экспериментальная проверка показала, что простой ГА с высокой долей вероятности позволяет получить оптимальное решение для задач малой (до 70 переменных) размерности. В случае получения в качестве решения локального экстремума отклонение от оптимума при том же времени решения составляет до 1,5 %.
На рисунке 5 представлена зависимость времени формирования одного поколения особей в ГА от размерности (числа переменных) решаемой задачи.
Из таблицы 2 и рисунка 5 видно, что с ростом числа переменных решаемой задачи время формирования одного поколения ГА растет экспоненциально. Данное обстоятельство позволяет судить о том, что время решения задач ГА будет нелинейно расти с ростом размерности задач. Степень нелинейности зависит от выбранных параметров алгоритма. Кроме того, с ростом размера популяции время решения задачи растет в квадратичной зависимости. Качество получаемого решения при использовании простого ГА вследствие сходимости к случайному локальному экстремуму может существенно варьироваться в зависимости от результата начальной инициализации исходной популяции [17, 22].
 Кроме того, из таблицы 3 видно, что с ростом размерности задачи выше 100 переменных область поиска решения столь существенно расширяется, что вероятность получения оптимального решения простым ГА значительно снижается независимо от выбора параметров алгоритма.
Кроме того, из таблицы 3 видно, что с ростом размерности задачи выше 100 переменных область поиска решения столь существенно расширяется, что вероятность получения оптимального решения простым ГА значительно снижается независимо от выбора параметров алгоритма.
Наилучшие схемы репродукции – случайный отбор и адаптивная (обеспечивают наискорейшее достижение оптимального решения при минимальном количестве итераций). При этом эффективность адаптивной схемы растет по сравнению со случайной с ростом размерности задачи. Это объясняется несколько большим разнообразием особей в исходной популяции, получаемым при использовании адаптивной схемы. Данная схема показывает более стабильный по качеству получаемого решения результат. При этом время решения незначительно выше, чем при использовании случайной схемы.
В связи с тем, что с ростом размерности решаемых задач простой ГА в большинстве случаев получает в качестве решения локальный экстремум, значение и близость которого к оптимальному существенно зависят от результатов начальной ини- циализации исходной популяции, для получания более стабильного результата предлагается использовать островной ГА (ОГА), являющийся модификацией простого ГА [23].
Сущность ОГА заключается в следующем. Одновременно и независимо друг от друга (параллельно) работают несколько простых ГА со своими популяциями. Каждый из них вследствие случайной начальной инициализации исходной популяции сходится к своему локальному экстремуму (острову). С определенной периодичностью (через определенное число поколений) по определенной схеме ГА обмениваются заданным числом лучших особей (осуществляется миграция особей), после чего процесс решения продолжается. Совокупность шагов алгоритма, завершающаяся обменом лучшими особями между островами (миграцией особей), составляет одну итерацию ОГА. Подобная схема позволяет обеспечить выход простых ГА в каждом из островов из области локального экстремума, обеспечить большее разнообразие особей в популяциях и с большей вероятностью получить лучшее решение (в том числе достичь глобального экстремума). В качестве схемы миграции особей чаще всего используются миграция с топологией полной сети, миграция с топологией кольца и их модификации [22, 23].
Введем обозначения: NLnd – число островов; NStep – число итераций ОГА.
ОГА с миграцией особей с топологией кольца состоит из следующих шагов.
1. Для каждого k-го острова (k = 1, 2, ..., NLnd) выполнить инициализацию исходной популяции путем заполнения ее особями, сгенерированными случайным образом (в исходную популяцию не включаются нежизнеспособные особи, повторное включение уже имеющейся особи не допускается) и формирование элитной популяции объемом Lel особей.
2. i = 0.
3. Для каждого острова (k = 1, 2, ..., NLnd) осуществляется последовательная эволюция поколений в количестве Ngen (выполнение простого ГА с заданной схемой репродукции).
4. Если NLnd > 1, для каждого k-го острова (k = 1, 2, ..., NLnd – 1) осуществляется перенос m (m = Lel/2) лучших особей из элитной популяции в исходную популяцию j-го (j = k + 1) острова путем замещения худших особей. Для случая k = NLnd осуществляется перенос лучших особей в 1-й остров.
5. i = i+1.
6. Если i < NStep, перейти к п. 3. В противном случае к п. 7.
7. Сформировать результирующую популяцию из особей, составляющих элитные популяции каждого из островов.
8. Из результирующей популяции выбрать лучшую особь – результат решения.
9. Конец.
Помимо адаптивной схемы репродукции, возможно использование ее упрощенного варианта – смешанной или гибридной схемы, при которой вариант селекции и кроссинговера для каждого острова выбирается при инициализации случайно и однократно.
Результаты экспериментальной проверки эффективности ОГА для решения задач дискретного линейного целочисленного программирования с булевыми переменными представлены в таблицах 4, 5 и на рисунках 6–8.

 В таблице 4 показаны экспериментально по- лученные параметры ОГА при решении задач обеспечения устойчивости функционирования РИС различной размерности, обеспечивающие максимально возможные шансы получения оптимального решения [22]. Из таблицы видно, что для получения решения максимального качества в ОГА количество островов должно быть не меньше 0,025N, количество особей в популяции – 0,6N, количество поколений в итерации должно быть в интервале от 0,9N до 1,2N, число итераций – не меньше 0,05N.
В таблице 4 показаны экспериментально по- лученные параметры ОГА при решении задач обеспечения устойчивости функционирования РИС различной размерности, обеспечивающие максимально возможные шансы получения оптимального решения [22]. Из таблицы видно, что для получения решения максимального качества в ОГА количество островов должно быть не меньше 0,025N, количество особей в популяции – 0,6N, количество поколений в итерации должно быть в интервале от 0,9N до 1,2N, число итераций – не меньше 0,05N.
В таблице 5 представлены результаты решения задач различной размерности ОГА с применением параметров алгоритма, приведенных в таблице 2. Из таблицы 5 видно, что ОГА с достаточно высокой степенью вероятности (по сравнению с простым ГА) получает оптимальное решение задач, в том числе большой размерности (число переменных более 150). В случае получения локального экстремума отклонение от оптимального решения не превышало 0,2 %.
 На рисунке 6 показана зависимость значения целевой функции решаемой задачи (размерность 150´4) от числа итераций. ОГА осуществляет последовательное приближение к глобальному экстремуму. При этом с 4-й итерации скорость прироста качества получаемого решения существенно снижается. Это свидетельствует о том, что в случае жесткого лимита времени, отводимого на решение задачи, когда можно удовлетвориться рациональным (квазиоптимальным) решением, достаточно использования 4-5 итераций алгоритма для данной размерности задач, что позволит сократить время поиска решения не менее чем на 40–60 %.
На рисунке 6 показана зависимость значения целевой функции решаемой задачи (размерность 150´4) от числа итераций. ОГА осуществляет последовательное приближение к глобальному экстремуму. При этом с 4-й итерации скорость прироста качества получаемого решения существенно снижается. Это свидетельствует о том, что в случае жесткого лимита времени, отводимого на решение задачи, когда можно удовлетвориться рациональным (квазиоптимальным) решением, достаточно использования 4-5 итераций алгоритма для данной размерности задач, что позволит сократить время поиска решения не менее чем на 40–60 %.
Время решения задачи ОГА линейно растет с увеличением числа островов.
На рисунках 7 и 8 представлены результаты работы адаптивной схемы в ОГА при решении задачи размерности 100´4.


К 5-6-й итерациям процедура адаптации сходится к выбору одной из схем отбора особей или их устойчивой комбинации. Аналогичная ситуация наблюдается в адаптации выбора кроссинговеров к 6–8-й итерациям алгоритма. Это может свидетель- ствовать о том, что ОГА к 7-й итерации осуществляет достаточное и устойчивое сближение к локальному экстремуму в каждом из островов. При этом миграция особей между островами до схождения к локальному экстремуму не оказывает кардинального влияния на работу схемы адаптации и лишь улучшает состав популяции, обеспечивая снижение скорости схождения к ближайшему локальному экстремуму. После 5–7-й итераций (когда острова в значительной степени приблизились к локальным экстремумам) обмен лучшими осо- бями приводит к кратковременному выходу схемы адаптации из равновесного состояния.
Применение триадных кроссинговеров с учетом схемы и с использованием в качестве маски кроссинговера лучшей особи не дают требуемого качества решения; и при использовании адаптивной схемы репродукции, и в большинстве случаев к 3-4-й итерации ОГА отсекаются от применения. При этом количество лучших особей, полученных с применением универсального кроссинговера, в популяциях во всех островах ОГА составляет порядка 46 %.
На рисунках 9–11 представлена сравнительная оценка влияния исходных данных на время решения задачи ОГА и методом ветвей и границ. Из рисунка 9 видно, что для больших размерностей (более 150 переменных) время решения задачи ОГА растет не так быстро, как при методе ветвей и границ, в том числе с определением порядка ветвления переменных, что говорит об эффективности и перспективности применения ОГА для получения точного решения задач большой размерности.

Из рисунка 10 видно, что с ростом числа огра- ничений в решаемой задаче время решения ОГА возрастает по линейному закону и носит менее выраженный характер по сравнению с методом ветвей и границ. Для размерности задач с количеством ограничений меньше 4 время решения задачи методом ветвей и границ с определением порядка ветв- ления переменных меньше, чем ГА, это объясняется меньшей вычислительной сложностью данного метода для задач малой размерности (с малым числом ограничений).
 На рисунке 11 представлена оценка влияния жесткости ограничений в решаемой задаче на время решения задач. Из рисунка видно, что изменение жесткости ограничений не оказывает существенного влияния на время решения задачи ОГА. При этом время решения задачи ОГА оказывается ниже (до 20 %) времени решения той же задачи методом ветвей и границ с определением порядка ветвления переменных при значении жесткости ограничений в интервале 40–50 %.
На рисунке 11 представлена оценка влияния жесткости ограничений в решаемой задаче на время решения задач. Из рисунка видно, что изменение жесткости ограничений не оказывает существенного влияния на время решения задачи ОГА. При этом время решения задачи ОГА оказывается ниже (до 20 %) времени решения той же задачи методом ветвей и границ с определением порядка ветвления переменных при значении жесткости ограничений в интервале 40–50 %.
В таблице 6 и на рисунке 12 представлены результаты оценки зависимости влияния точности получаемого решения на общее время решения задачи ОГА. Изменение точности получаемого решения осуществлялось путем варьирования значений параметров ОГА, представленных в таблице 2. Для каждого варианта параметров ОГА задача каждой размерности решалась по 10 раз.

Из таблицы 6 и рисунка 12 видно, что ухудшение качества полученного ОГА решения всего на 0,5 % от оптимального приводит к сокращению времени получения рационального решения в 3–6 раз по сравнению со временем получения оптимального решения. При этом с ростом размерности решаемой задачи данный эффект становится более явным. Это обстоятельство позволяет сделать вывод о перспективности и целесообразности применения ОГА для оперативного получения рацио- нального (квазиоптимального) решения в условиях жестких временных ограничений.
Таким образом, результаты экспериментальной проверки показали, что применение ОГА для решения задач обеспечения устойчивости функционирования РИС эффективно для задач большой размерности (с числом переменных более 150), задач с жесткостью ограничений в интервале 40–50 %, а также в условиях жестких временных ограничений. В качестве схемы отбора особей целесообразно использовать случайный отбор или адаптивную схему. Использование простого ГА целесообразно для решения задач малой размерности (число переменных до 70). Использование ОГА для получения рационального решения поставленных задач позволит сократить время решения задачи размерности 100´4 по сравнению с применением точных методов в 5 раз с обеспечением размера относительной ошибки в 0,7 % и в 6–10 раз с обеспечением величины относительной ошибки в 1,5 %. С ростом размерности решаемых задач выигрыш по времени получения рационального решения становится еще более существенным.
Метод ветвей и границ целесообразно применять для решения задач обеспечения устойчивости функционирования РИС на этапах их проектирования, когда необходимо получить оптимальное решение и отсутствуют строгие ограничения на время его получения. На этапе эксплуатации, при реконфигурировании системы передачи и обработки данных, в условиях жесткого лимита времени на время реакции системы на отказы и сбои целесообразно применять метод получения рационального (квазиоптимального) решения, основанный на использовании ОГА, который в отличие от существующих приближенных методов обеспе- чивает за счет обоснованного выбора параметров алгоритма гарантированное получение рационального (квазиоптимального) решения (серии рациональных решений) за время, не превышающее заданное.
Литература
1. Воронин A.A., Морозов Б.И. Надежность информационных систем. СПб: Изд-во СПбГТУ, 2001. 89 с.
2. Бройдо В.Л. Вычислительные системы, сети и телекоммуникации. 2-е изд. СПб: Питер, 2004. 705 с.
3. Николаев В.И., Брук В.М. Системотехника: методы и приложения. Л.: Машиностроение, 1985. 199 с.
4. Есиков Д.О. Обеспечение устойчивого функционирования вычислительных систем за счет обеспечения высоконадежного хранения данных // Фундаментальные и прикладные исследования, разработка и применение высоких технологий в промышленности: сб. стат. XV Междунар. науч.-практич. конф. СПб: Изд-во Политехн. ун-та, 2013. С. 110–118.
5. Повзнер Л.Д. Теория систем управления. М.: Изд-во МГГУ, 2002. 472 с.
6. Данилкин Ф.А., Есиков Д.О. Оптимизация распределения информационных ресурсов в вычислительной сети // Инновации в технологиях и образовании: сб. стат. V Междунар. науч. конф. Белово: Изд-во КузГТУ, 2012. Ч. 2. 328 с.
7. Киселев В.Д., Есиков О.В., Кислицын А.С. Теоретические основы оптимизации информационно-вычислительного процесса и состава комплексов средств защиты информации в вычислительных сетях; [под ред. Е.М. Сухарева]. М.: Полиграфсервис XXI век, 2003. 198 c.
8. Есиков Д.О. Задачи обеспечения устойчивости функционирования распределенных информационных систем // Программные продукты и системы. 2015. № 4. С. 133–142.
9. Сергиенко И.В., Гуляницкий Л.Ф., Сиренко С.И. Классификация прикладных методов комбинаторной оптимизации // Кибернетика и системный анализ. 2009. № 5. С. 71–83.
10. Алексеев О.Г. Комплексное применение методов дискретной оптимизации. М.: Наука, 1987. 248 с.
11. Есиков Д.О. Оценка влияния предварительного определения порядка ветвления переменных на эффективность метода ветвей и границ // Междисциплинарные исследования в области математического моделирования и информатики: матер. науч.-практич. конф. Ульяновск: SIMJET, 2013. С. 17–21.
12. Бабаев А.А. Организация поиска решений на деревьях детерминированной структуры // Электронное моделирование. 1985. Т. 7. № 1. С. 19–25.
13. Есиков Д.О. Повышение эффективности метода ветвей и границ выбором способа организации компьютерных вычислений // Интеллектуальные и информационные системы (Интеллект 2013): сб. стат. Всерос. науч.-практич. конф. Тула: Изд-во ТулГУ, 2014. С. 143–147.
14. Yesikov D.O. Increase of level of stability of functioning of systems of storage and data processing at the expense of realization of actions for ensuring safety of information. Proc. 3rd Intern. Conf. High Performance Computing (HPC-UA 2013). Ukraine, Kiev, 2013, pp. 416–420.
15. Есиков О.В., Есиков Д.О. Математические модели и алгоритмы обеспечения сохранности информации // Изв. Тульского гос. ун-та: Технические науки. 2013. Вып. 9. Ч. II. С. 110–118.
16. Есиков Д.О., Ивутин А.Н. Программа решения задач целочисленного линейного программирования с булевыми переменными. Свид. о гос. регистр. прогр. для ЭВМ № 2014619322. Госрегистр. в Реестре прогр. для ЭВМ 15.09.2014.
17. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы; [пер. с пол. И.Д. Рудинского]. М.: Горячая линия–Телеком, 2004. 383 с.
18. Holland J.H. Adaptation in Natural and Artificial Systems: 2nd ed. Cambridge, MA: MIT Press, 1992.
19. Гладков Л.А., Курейчик В.В., Курейчик В.М. Генетические алгоритмы. М.: Физматлит, 2006. 320 с.
20. Нгуен Минь Ханг. Применение генетического алгоритма для задачи нахождения покрытия множества // Труды ИСА РАН. 2008. № 33. С. 206–219.
21. Есиков Д.О., Ивутин А.Н., Ларкин Е.В. Программа решения задач целочисленного программирования с булевыми переменными островным генетическим алгоритмом. Свид. о гос. регистр. прогр. для ЭВМ № 2015663468. Госрегистр. в Реестре прогр. для ЭВМ 18.12.2015.
22. Yesikov D.O., Ivutin A.N. Rational values of parameters of island genetic algorithms for the effective solution of problems of ensuring stability of functioning of the distributed information systems. Proc. 5th Mediterranean Conf. on Embedded Computing (MECO) 2016, pp. 309–312. DOI: 10.1109/MECO.2016.7525769.
23. Карпенко А.П. Популяционные алгоритмы глобальной поисковой оптимизации. Обзор новых и малоизвестных алгоритмов // Информационные технологии. 2012. № 7. С. 13–15.



 , где Ктр – требуемое значение показателя качества функционирования системы; Кдфi – значение показателя качества функционирования системы в условиях воздействия i-гo дестабилизирующего фактора [2, 3].
, где Ктр – требуемое значение показателя качества функционирования системы; Кдфi – значение показателя качества функционирования системы в условиях воздействия i-гo дестабилизирующего фактора [2, 3]. , где I – количество учитываемых дестабилизирующих факторов в системе.
, где I – количество учитываемых дестабилизирующих факторов в системе.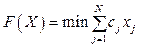 (1)
(1) i = 1, 2, …, M, (3)
i = 1, 2, …, M, (3)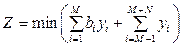 (5)
(5)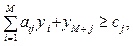 j = 1, 2, …, N, (6)
j = 1, 2, …, N, (6)





 , где g1i и g2i – значения i-х генов 1-й и 2-й особей.
, где g1i и g2i – значения i-х генов 1-й и 2-й особей.
 ,
,  – значения функции приспособленности родительских особей. g1 и g2 выбираются в соответствии с текущей схемой отбора особей, g3 – случайным образом из особей родительской популяции.
– значения функции приспособленности родительских особей. g1 и g2 выбираются в соответствии с текущей схемой отбора особей, g3 – случайным образом из особей родительской популяции. и
и  по следующим правилам.
по следующим правилам.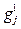 =
= 
 , то
, то  P0(j) ³
P0(j) ³ =
= =
=  , то
, то  , если
, если  и
и  , для которых выполняется расчет значения функции принадлежности. Если rnd > Pc, присвоение
, для которых выполняется расчет значения функции принадлежности. Если rnd > Pc, присвоение  Если rnd2 ≤Pm, выполнение операции мутации с хромосомой
Если rnd2 ≤Pm, выполнение операции мутации с хромосомой 









