Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Инструментальная среда эволюционного моделирования
Аннотация:
Abstract:
| Авторы: Курейчик В.В. (vkur@sfedu.ru) - Южный федеральный университет (зав. кафедрой), Таганрог, Россия, доктор технических наук, Сороколетов П.В. () - , Хабарова И.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 15072 |
Версия для печати Выпуск в формате PDF (1.30Мб) |
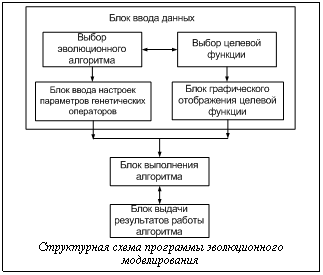
Эволюционные вычисления являются адаптивными алгоритмами, что позволяет применять их в нелинейных задачах высокой размерности при отсутствии требований к дифференцируемости оптимизируемой функции или полноты знаний о решаемой проблеме. Они отличаются устойчивостью при поиске решения оптимизационных задач искусственного интеллекта [1-4]. Для повышения качества решения оптимизационных задач используются эволюционные модели с динамическими параметрами [2,5]. При этом в процессе эволюции размер популяции и длительность жизни каждого индивида (альтернативного решения) меняется в зависимости от внешней среды. Это позволяет гибко реагировать на любые внешние параметры и повышает эффективность вычислений. В работе описана инструментальная среда по исследованию характеристик эволюционных алгоритмов (ЭА) с динамическими параметрами. Общая структурная схема инструментальной среды эволюционного моделирования приведена на рисунке. Программа для исследования эволюционных алгоритмов с динамическими параметрами DYNGEN содержит в себе [6]: - панели для выбора алгоритма для исследования и вида целевой функции; - панель настроек параметров для конкретного ЭА; - панель работы алгоритма, позволяющую отображать в процессе работы алгоритма значение исходных данных задачи, значение целевой функции, график максимальной и средней целевой функции по популяции и прогону; для визуальной оценки выполнения алгоритма предусмотрен вывод результатов на экран в виде графиков зависимости целевой функции от поколения [6]. Выбор ЭА включает: простой генетический алгоритм (ПГА), ЭА с переменным временем жизни (ЭА1), ЭА с динамическим размером популяции (ЭА2), ЭА с логистической моделью (ЭА3), ЭА с последствием, поколенческий (ЭА4), ЭА с логистическими моделями (ЭА5) [2,5,6]. Программой предусмотрен просмотр выбранной целевой функции для визуального представления задачи. Следующим этапом является ввод параметров. Параметры подразделяются на общие и дополнительные. К общим относятся: начальный размер популяции, вероятности генетических операторов, уровень репродукции, число генерируемых поколений, число отдельных запусков алгоритма, тип останова (по номеру поколения, по достижению максимума целевой функции, по отсутствию изменений) и разрядность хромосом (альтернативных решений). Дополнительные параметры для конкретного алгоритма: · для ЭА1 – минимальное время жизни хромосомы, параметр внешних воздействий, размер архива; · для ЭА2 с динамическим размером популяции – число удаляемых хромосом; · для ЭА3 – шаг изменения уровня репродукции; · для ЭА4 – возраст хромосомы; · Для программной реализации использован компилятор Delphi 5.0 для 32-разрядных систем Windows, что позволило обеспечить удобный интерфейс пользователя и визуализацию работы алгоритмов. Цель экспериментального исследования – найти оптимальные параметры предложенных алгоритмов, при которых решение данной задачи (глобальный и близкие ему локальные максимумы функций) становится возможным или улучшается по сравнению с ПГА. Объектами исследований в данной работе являются ЭА с динамическими параметрами [6]. Критерий эффективности алгоритма есть максимальное значение целевой функции, выраженное в процентах. В ходе работы были исследованы ЭА при различных значениях варьируемых динамических параметров, подобраны их оптимальные значения для нахождения глобального оптимума тестовых функций. Выбор целевой функции включает функции с одной и двумя переменными. Для проведения экспериментальных исследований рассмотрим следующие функции: f1(x)=x; f2(x)=xn, nÎ[2,4]; f3(x)=x2-y2;
В таблице показаны экспериментальные результаты оптимизации данных функций. Каждый эксперимент проводился повторно 100 раз до достижения 10 поколений. В таблицу занесены средние значения полученных результатов в процентах.
Можно сделать вывод, что из предложенных алгоритмов лучшие результаты показал ЭА5 для всех исследуемых функций, а введение динамических параметров позволяет повысить эффективность генетического поиска и обеспечить его устойчивость. Найденное максимальное и среднее значение целевой функции увеличивается в среднем на 10% по сравнению с ПГА. Использование динамических параметров при эволюционном моделировании повышает эффективность ЭА, обеспечивая сохранение найденных лучших решений. Это объясняется тем, что жесткие связи в модели приводят к замкнутости поиска, а введение динамических переменных позволяет устранить проблемы преждевременной сходимости и потери найденного лучшего решения. Список литературы 1. Тарасов В.Б. От многоагентных систем к интеллектуальным организациям: философия, психология, информатика. -М.: Эдиториал УРСС, 2002. -352с. 2. Зинченко Л.А., Курейчик В.М. Многоальтернативные генетические алгоритмы поиска экстремума функции //Изв. РАН. Теории и системы управления. – 2003. - № 4. - С. 82-91. 3. Гладков Л.А., Курейчик В.В., Курейчик В.М. Генетические алгоритмы: Учебное пособие. / Под ред. В.М. Курейчика. - М: Физматлит, 2006. 4. Курейчик В.В. Эволюционные, синергетические и гомеостатические методы принятия решений: Монография. - Таганрог: Изд-во ТРТУ, 2001. 5. Курейчик В.М., Зинченко Л.А. Эволюционное моделирование с использованием динамических параметров // Тр. VII нац. конф. по искусствен. интеллекту. - М.: Физматлит, 2000. - С. 516-523. 6. Хабарова И.В.. Разработка среды эволюционного моделирования с динамическими параметрами DYNGEN //Изв. ТРТУ. – Таганрог. - 2002. - № 3. - С. 273. |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=429&page=article |
Версия для печати Выпуск в формате PDF (1.30Мб) |
| Статья опубликована в выпуске журнала № 4 за 2006 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Нейроподобная сеть для решения задачи оптимизации антенной решетки
- Оценка защищенности информации от несанкционированного доступа при помощи имитационной модели системы защиты информации
- Гибридная система поиска решений на основе временных продукционных правил
- Формирование программ развития больших систем административно-организационного управления
- Функционально-информационные модели бухгалтерского учета
Назад, к списку статей



 для ЭА5 – возраст хромосомы, номер шага для уменьшения размера популяции.
для ЭА5 – возраст хромосомы, номер шага для уменьшения размера популяции.
 .
.