Синтез нейро-нечетких сетей с группировкой признаков
| Субботин С.А. (subbotin@zntu.edu.ua) - Запорожский национальный технический университет, Запорожье, Украина, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
При построении распознающих моделей, особенно в задачах классификации изображений и диагностики, нередко возникает ситуация, когда некоторые признаки по отдельности оказывают слабое влияние на выходной признак, а совместно влияют на него сильно [1]. Это может объясняться тем, что отдельные признаки, доступные нам для наблюдения и измерения, являются косвенными проявлениями более важных признаков (факторов), недоступных для наблюдения и (или) измерения. Попытка построения модели по косвенным признакам может быть успешной, но такая модель чаще всего крайне неудобна для последующего анализа, поскольку адекватно не отображает реальные зависимости между признаками либо выделяет факторы неявно. Поэтому представляется целесообразным перед построением модели разбивать признаки на группы в зависимости от значения некоторой меры их взаимной связи, производить обобщение признаков каждой группы путем расчета значения некоторой свертки и далее строить модель зависимости выходного признака от значений сверток для каждой группы признаков. Это позволит не только упростить последующий анализ модели, но и существенно сократить размерность обучающей выборки, а следовательно, упростить распознающую модель. Группирование признаков предлагается осуществлять путем выполнения шагов 1-10. Шаг 1. Задать обучающую выборку , x={xs}, xs={xsj}, y={ys}, где xs – s-й экземпляр выборки; xsj – значение j-го признака s-го экземпляра выборки; ys – значение целевого признака s-го экземпляра выборки. Шаг 2. Определить значения показателя информативности для каждого признака Ij, j=1,2,…,N.. Шаг 3. Для i,j=1, 2,…,N, i≠j, найти расстояния между признаками в пространстве экземпляров обучающей выборки d(xj,xi):
Шаг 4. Найти коэффициенты эквивалентности признаков eji, i,j=1,2,…,N, i≠j. Принять eji=eji-1. Шаг 5. Установить номер текущей группы g=0. Шаг 6. Если Шаг 7. Найти признак xi: Ii=max Ij, j=1,2,…,N. Шаг 8. Установить g=g+1. Добавить новую группу признаков Gg. Включить в группу Gg признак xi. Установить: Ii=-1. Шаг 9. Если Оператор F может быть определен как:
Параметры
где width – ширина изображения; div – операция целочисленного деления; mod – операция "остаток от целочисленного деления". Шаг 10. Останов. Для оценивания информативности признаков и определения характеристик для нахождения коэффициентов эквивалентности признаков предлагается использовать метод, заключающийся в выполнении шагов 1-12 [2]. Шаг 1. Инициализация. Задать обучающую выборку экземпляров x, состоящую из S экземпляров xs, где s – номер экземпляра, s=1,2,...,S. Каждый s-й экземпляр будем характеризовать набором значений N признаков xsj, где j – номер признака s-го экземпляра, j=1,2,...,N. Кроме того, каждому экземпляру xs сопоставим целевой признак ys* – номер класса s-го экземпляра. Обучающую выборку представим в виде массива, в котором признаки линеаризованы по строкам, а экземпляры – по столбцам, а также зададим соответствующий массив y*={ys*}, содержащий номера классов, сопоставленные экземплярам обучающей выборки. Создать массив {Dj}, равный по размеру количеству признаков N, элементы которого будут содержать число интервалов для каждого признака. Установить Dj=0, j=1,2,...,N, где j – номер текущего признака. Занести количество экземпляров обучающей выборки в переменную S. Установить номер текущего признака i=1. Шаг 2. Если i Шаг 3. Занести в буфер признака x вектор значений i-го признака из обучающей выборки: x(j)=xsi; занести в буфер класса y копию массива y*: y(s)=ys*, s=1,2,...,S. Шаг 4. Отсортировать массивы x и y в порядке возрастания массива x (шаги 4.1-4.7 реализуют простейший алгоритм пузырьковой сортировки, который можно заменить на практике более быстродействующим алгоритмом). Шаг 4.1. Установить номер текущего экземпляра s=1. Шаг 4.2. Если s Шаг 4.3. Установить номер текущего экземпляра k=s+1. Шаг 4.4. Если k Шаг 4.5. Если x(s)>x(k), тогда установить z=x(s), x(s)=x(k), x(k)=z, z=y(s), y(s)=y(k), y(k)=z, где z – буферная переменная. Шаг 4.6. Установить: k=k+1. Перейти на шаг 4.4. Шаг 4.7. Установить s=s+1. Перейти на шаг 4.2. Шаг 5. Установить s=1, k=1. Шаг 6. Если s Шаг 7. Пока s Шаг 8. Если s=S и y(s)=y(s-1), тогда установить K(i,k)=y(s), A(i,k)=at, B(i,k)=x(s), k=k+1, s=s+1, перейти на шаг 10. Здесь K(i,k) – номер класса, сопоставленный экземплярам обучающей выборки, значение i-го признака которых попадает внутрь k-го интервала; A(i,k) и B(i,k) – левая и правая границы k-го интервала i-го признака соответственно. Шаг 9. Если s < S и y(s) Шаг 10. Перейти на шаг 6. Шаг 11. Установить i=i+1, перейти на шаг 2. Шаг 12. Останов. В результате выполнения шагов 1–12 для обучающей пары {x,y} мы получим массив {Dj}, содержащий для каждого признака количество интервалов, на которые он разбивается, а также массивы {A(i,k)}, {B(i,k)} и {K(i,k)}, содержащие информацию о границах интервалов и номерах классов, сопоставленных им для всех признаков. Показатели информативности признаков Ij определим по формуле:
Коэффициент эквивалентности между k-м интервалом значений i-го признака для s-го экземпляра и q-м интервалом значений j-го признака для g-го экземпляра определим по формуле:
s=1,2,...,S; g=1,2,...,S; i=1,2,...,N; j=1,2,...,N; k=1,2,...,ki; q=1,2,...,kj.
i=1,2,...,N; j=1,2,...,N; k=1,2,...,ki; q=1,2,...,kj. Коэффициент взаимной эквивалентности между k-м интервалом значений i-го признака и q-м интервалом значений j-го признака определим по формуле:
i=1,2,...,N; j=1,2,...,N; k=1,2,...,ki; q=1,2,...,kj; где Ni,k – количество экземпляров обучающей выборки, попавших в k-й интервал значений i-го признака. Коэффициент взаимной эквивалентности между i-м и j-м признаками для всех экземпляров выборки определим по формуле:
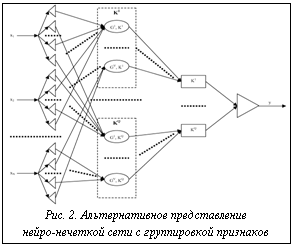
После группирования признаков можно выполнить построение распознающей модели. В данной работе для построения распознающих моделей предлагается использовать нейро-нечеткие сети, которые сочетают в себе способности к обобщению и обучению, а также обладают свойством логической прозрачности, то есть легко поддаются анализу и пониманию человеком. В случае когда целью является определение семантики скрытых признаков (факторов, соответствующих группам), целесообразно синтезировать сеть, представленную на рисунке 1.
На входы предложенных сетей будут подаваться значения соответствующих признаков распознаваемого экземпляра. На первом слое обеих сетей расположены блоки определения принадлежности распознаваемого экземпляра к нечетким термам. Нечеткие термы можно сформировать путем задания функций принадлежности для интервалов значений признаков В качестве функций принадлежности предлагается использовать трапециевидные функции:
либо П-образные функции:
где
Второй слой содержит нейроны, определяющие принадлежность распознаваемого экземпляра по группам признаков каждого класса. Количество нейронов второго слоя N2=VQ, где V – количество групп признаков; Q – количество классов. Третий слой сети содержит нейроны, объединяющие принадлежности по различным группам признаков в принадлежности к классам. Количество нейронов третьего слоя N3=Q. Единственный нейрон четвертого слоя сети осуществляет объединение принадлежностей к классам и выполняет дефазификацию. Дискриминантные функции нейронов обеих сетей будут определяться следующим образом:
Функции активации нейронов сети будут определяться по формулам:
Весовые коэффициенты нейронов
Для альтернативного представления сети весовые коэффициенты нейронов
При решении задач распознавания для трех и более классов целесообразным может оказаться построение не единой модели с выходом, принимающим три и более значений, а синтез отдельных моделей для определения принадлежности к каждому классу. Это позволит формировать наборы групп признаков, своих для каждого класса. Например, в задачах распознавания изображений может оказаться, что один и тот же признак может относиться к разным группам признаков для разных классов. Построение отдельных моделей для каждого класса позволит сохранить внутриклассовую семантическую нагрузку признаков, в то время как построение единой модели для всех классов может привести к частичной потере семантики признаков. Для построения отдельных моделей для каждого класса необходимо в исходной выборке данных заменить значения целевого признака на "1", если экземпляр принадлежит к классу, для определения которого строится модель, и на "0" в противном случае. После чего можно применить для построения модели по каждому классу тот же метод, что и для выхода, принимающего много значений. Предложенный метод позволяет строить нейро-нечеткие сети с хорошими обобщающими способностями, не требующие итеративной оптимизации параметров функций принадлежности, что исключает проблему попадания в локальные минимумы целевой функции. Список литературы 1. Дубровин В.И., Субботин С.А., Богуслаев А.В., Яценко В.К. Интеллектуальные средства диагностики и прогнозирования надежности авиадвигателей: Монография. – Запорожье: ОАО "Мотор-Сич", 2003. – 279 с. 2. Дубровин В.И., Субботин С.А. Алгоритм классификации с оценкой значимости признаков // Радiоелектронiка. Iнформатика. Управлiння. - 2001. - № 2. - С. 145-150. 3. Лакин Г.Ф. Биометрия: Учеб. пособие для биол. спец. вузов. – М.: Высш. шк., 1990. – 352 с. |
http://swsys.ru/index.php?id=430&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Гибридная система поиска решений на основе временных продукционных правил
- Формирование программ развития больших систем административно-организационного управления
- Формулировка задачи планирования линейных и циклических участков кода
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- Информационно-вычислительный комплекс по применению мембран в биотехнологии


 xj:
xj:  Ij≠-1 и
Ij≠-1 и 
 могут быть определены по соответствующим формулам:
могут быть определены по соответствующим формулам:



 N, тогда перейти на шаг 3, иначе – перейти на шаг 12.
N, тогда перейти на шаг 3, иначе – перейти на шаг 12. y(s+1), тогда установить K(i,k) = y(s), A(i,k)=at, B(i,k)=x(s), k=k+1, s=s+1, Di=Di +1, в противном случае установить K(i,k)=y(s), A(i,k)=x(s), B(i,k)=x(s), k=k+1, s=s+1.
y(s+1), тогда установить K(i,k) = y(s), A(i,k)=at, B(i,k)=x(s), k=k+1, s=s+1, Di=Di +1, в противном случае установить K(i,k)=y(s), A(i,k)=x(s), B(i,k)=x(s), k=k+1, s=s+1. , j=1,2,...,N.
, j=1,2,...,N.
 Количество экземпляров с одинаковыми номерами классов, попавших одновременно в k-й интервал значений i-го признака и в q-й интервал значений j-го признака, определим по формуле:
Количество экземпляров с одинаковыми номерами классов, попавших одновременно в k-й интервал значений i-го признака и в q-й интервал значений j-го признака, определим по формуле:

 , i=1,2,...,N; j=1,2,...,N.
, i=1,2,...,N; j=1,2,...,N.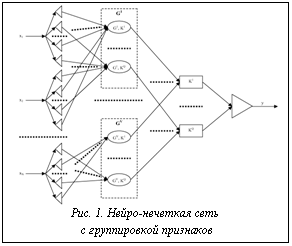 Предложенная сеть может иметь альтернативное представление (рис. 2), которое целесообразно использовать, если целью является установление влияния факторов на конкретный класс.
Предложенная сеть может иметь альтернативное представление (рис. 2), которое целесообразно использовать, если целью является установление влияния факторов на конкретный класс. , где i – номер признака; k – номер интервала значений i-го признака.
, где i – номер признака; k – номер интервала значений i-го признака.
 ,
, – S-образная функция, а
– S-образная функция, а  – Z-образная функция:
– Z-образная функция:

 ,
, =2, i=1,2,…,VQ;
=2, i=1,2,…,VQ; ,
,
 ,
, ,
,
 , где j – номер входа; i – номер нейрона;
, где j – номер входа; i – номер нейрона;  – номер слоя, нейро-нечеткой сети с группировкой признаков будут определяться по формуле:
– номер слоя, нейро-нечеткой сети с группировкой признаков будут определяться по формуле:


 будут определяться по формуле:
будут определяться по формуле: