Верификация программных и технических систем является сегодня одним из важнейших этапов их жизненного цикла. Для этих целей уже создано и успешно апробировано множество различных средств и методов разного типа сложности и применимости. Однако наиболее часто используемыми и востребованными, как правило, остаются средства формальной верификации, работа которых может быть в той или иной мере автоматизирована в отличие от, например, динамических методов верификации и экспертиз.
 Среди формальных методов верификации наибольшую популярность за свою практичность и эффективность получил так называемый метод проверки на моделях Model Checking [1, 2]. Базовая идея алгоритма этого метода для требований к системе, заданных в виде формул логики линейного времени LTL [3, 4], представлена в виде схемы на рисунке 1.
Среди формальных методов верификации наибольшую популярность за свою практичность и эффективность получил так называемый метод проверки на моделях Model Checking [1, 2]. Базовая идея алгоритма этого метода для требований к системе, заданных в виде формул логики линейного времени LTL [3, 4], представлена в виде схемы на рисунке 1.
Использование данной схемы в чистом виде при верификации моделей систем больших размеров (более 220 состояний) во многих случаях может приводить к тому, что верификация либо будет выполняться очень долго, либо вообще не будет выполнена. Для решения данных проблем и достижения более высокой производительности сегодня существует ряд специальных средств и методов, которые за счет определенных манипуляций над моделью системы и/или над требованиями к ней позволяют добиться приемлемой производитель- ности [5–7]. В частности, одним из инструментов повышения эффективности выполнения верификации является предложенный в работе [8] метод абстракции и унификации RLTL-моделей (Recursive Linear Temporal Logic).
В данной статье авторами предложен принципиально иной подход к повышению производи- тельности процесса верификации, который явля- ется результатом использования предложенной в [9] новой нотации LTL, обозначаемой как RLTL. Показана возможность выполнения на базе RLTL и самого процесса верификации, что позволит упростить алгоритм верификации методом Model Checking и привести его к виду, представленному на рисунке 2.

RLTL-нотация
Рассмотрим представления основных базовых конструкций логики LTL, заданных в RLTL-нотации:
LTL RLTL
φ1 ∨ φ2 φ1 + φ2
φ1 ∧ φ2 {φ1, φ2}
Xφ ∆ ∘ φ
Запись {φ1, φ2} означает множество μ, состоящее из предикатов φ1 и φ2.
В RLTL приняты следующий бозначения.
∘ – оператор продолжения (конкатенация выражений), что позволяет использовать оператор X в неявном виде, а также упростить его восприятие, в частности, запись μ1 ∘ μ2 будет пониматься как «μ2 следует за μ1».
μ – множество выполнимых на конкретном этапе вычислительного процесса атомарных предикатов, задающих те или иные свойства системы.
∆ – предикат неопределенности, задающий неопределенное множество свойств системы μ, выполнимых на конкретном этапе вычислительного процесса. Отрицанием предиката неопределенности является некоторое другое неопределенное подмножество свойств μ', а отрицанием отрица- ния – некоторое третье неопределенное подмноже- ство μ''. Таким образом, отрицание предиката неопределенности является неполным, а каждое последующее отрицание дает неопределенное подмножество атомарных предикатов. Каждое из этих подмножеств ввиду своей неопределенности также может быть обозначено через ∆.
⊥ – оператор остановки вычислительного процесса. Это означает, что, как только данный оператор встречается в конкретный момент времени вычислительного процесса, в дальнейшем ни одно свойство системы не будет выполнено.
Сформулируем основные аксиомы нотации RLTL:
|
A1.
|
FFφ = Fφ
|
(FF)
|
|
A2.
|
GGφ = Gφ
|
(GG)
|
|
А3.
|
˥Fφ = G˥φ
|
(˥F)
|
|
A4.
|
˥Gφ = F˥φ
|
(˥G)
|
|
A5.
|
Gφ = φ ∘ Gφ
|
(G)
|
|
A6.
|
Fφ = φ + ∆ ∘ Fφ
|
(F)
|
|
A7.
|
Gφ + ˥Gφ = ∆
|
(+ G)
|
|
A8.
|
Fφ + ˥Fφ = ∆
|
(+ F)
|
|
A9.
|
Gφ1 ∘ φ2 = Gφ1
|
(G ∘)
|
|
A10.
|
Fφ1 ∘ φ2 = F(φ1 ∘ φ2)
|
(F ∘)
|
|
A11.
|
U(φ1, φ2) = φ2 + φ1 ∘ U(φ1, φ2)
|
(U)
|
|
А12.
|
˥(μ ∘ μ1) = ˥μ + ∆ ∘ ˥μ1
|
(˥μ ∘)
|
|
А13.
|
{μ, ∆} = μ
|
(∆)
|
|
A14.
|
{φ1, ∆ ∘ φ2} = φ1 ∘ φ2
|
(∆ ∘)
|
|
A15.
|
⌉μ = (∆ \ μ)
|
⌉μ
|
|
A16.
|
⊥ ∘ μ = μ ∘ ⊥ = ⊥
|
⊥ ∘
|
|
A17.
|
⊥ + μ = μ
|
⊥ +
|
Правила вывода в RLTL: R1. ˥∆ → ∆.
Лемма 1. Оператор F логики LTL, рекурсивное представление которого задано как Fq = q ∨ X(Fq), может быть представлен в RLTL-нотации в виде F' = q + ∆ ∘ F'.
Доказательство. Обозначим Fq через F'. Тогда F' = Fq = q ∨ X(Fq) = q ∨ X(F'). Отсюда, в соответствии с правилами представления формул LTL в RLTL, получаем: F' = q + ∆ ∘ F'. ■
Лемма 2. Оператор G логики LTL, рекурсивное представление которого задано как Gq = q ∧ X(Gq), может быть представлен в RLTL-нотации в виде F' = q ∘ F'.
Доказательство. Обозначим Gq через F'. Тогда F' = Gq = q ∧ X(Gq) = q ∧ X(F'). Отсюда, в соответствии с правилами представления формул LTL в RLTL, получаем
F' = {q, ∆ ∘ F'} = [A14] = q ∘ F'. ■
Лемма 3. Оператор U логики LTL, рекурсивное представление которого задано как pUq = q ∨ (p ∧ ∧ X(pUq)), может быть представлен в RLTL-нотации в виде F' = q + p ∘ F'.
Доказательство. Обозначим pUq через F'. Тогда F' = pUq = q ∨ (p ∧ X(pUq)) = q ∨ (p ∧ X(F')). Отсюда, в соответствии с правилами представления формул LTL в RLTL, получаем: F' = q + {p, ∆ ∘ F'} = [A14] = q + p ∘ F'. ■
Построение синхронной композиции двух систем рекурсивных уравнений
Идея верификации моделей систем, заданных на базе RLTL-нотации, практически ничем не отличается от верификации систем, заданных в виде автоматов Бюхи. Для того чтобы проверить, выполняется ли целевое требование, также заданное с помощью RLTL, на модели системы или нет, необходимо запустить две системы синхронно (модель и требование к ней) и следить за процессом их синхронной работы. Система, работающая синхронно, осуществляет переход в следующее состояние по некоторому символу p тогда и только тогда, когда вторая система также может выполнить переход из своего текущего состояния в некоторое новое состояние по символу p.
Сформулируем основные аксиомы, необходимые для построения синхронной композиции двух систем рекурсивных уравнений:
S1. μ1⊗μ2 = μ1, если μ1 ⊆ μ2,
μ2, если μ2 ⊆ μ1,
⊥ в противном случае,
S2. μ⊗⊥ = ⊥,
S3. μ⊗∆ = μ,
S4. (μ1 + μ2) ⊗ μ3 = (μ1 ⊗ μ3) + (μ1 ⊗ μ3),
S5. (μ1 ∘ μ2) ⊗ (μ3 ∘ μ4) = (μ1⊗μ3) ∘ (μ2⊗μ4).
Под символом ⊗ будем понимать оператор синхронной композиции. Все, что стоит справа или слева от данного оператора, должно выполняться синхронно, если это возможно.
Пример построения синхронной композиции
Дано.
Система A:
FA1 = a ∘ FA1 + b ∘ FA2,
FA2 = c ∘ FA1.
Система B:
FB1 = c + ∆ ∘ FB1.
Для построения синхронной композиции расширим систему A следующим образом, полагая, что в случае наступления события «c» система продолжит работать бесконечно долго, то есть зациклится: FB1 = c ∘ FB2 + ∆ ∘ FB1,
FB2 = ∆ ∘ FB2.
Решение.
Построение синхронной композиции A⊗B:
P1 = FA1⊗FB1 =
= (a⊗c) ∘ (FA1⊗FB2) + (a⊗∆) ∘ (FA1⊗FB1) +
+(b⊗c) ∘ (FA2⊗FB2) + (b⊗∆) ∘ (FA2⊗FB1) =
=⊥ ∘ (FA1⊗FB2) + (a⊗∆) ∘ P1 + ⊥ ∘ (FA2⊗FB2) +
+ (b⊗∆) ∘ P2 = ⊥ + a ∘ P1 + ⊥ + b ∘ P2 = a ∘ P1 + b ∘ P2.
P2 = FA2⊗FB1 = (c⊗c) ∘ (FA1⊗FB2) + (c⊗∆) ∘ (FA1⊗FB1) =
= (c⊗c) ∘ P3 + (c⊗∆) ∘ P1 = c ∘ P3 + c ∘ P1.
P3 = FA1⊗FB2= (a⊗∆) ∘ (FA1⊗FB2) + (b⊗∆) ∘ (FA2⊗FB2) =
= a ∘ P3 + b ∘ P4.
P4 = FA2⊗FB2=(c⊗∆) ∘ (FA1⊗FB2) = c ∘ P3.
Конечная синхронная композиция:
P1 = a ∘ P1 + b ∘ P2,
P2 = c ∘ P3 + c ∘ P1,
P3 = a ∘ P3 + b ∘ P4,
P4 = c ∘ P3.
Теорема 1. Пусть заданы две системы рекурсивных уравнений A и B, где P11, P12, …, P1n – множество метапеременных системы A; P21, P22, …, P2m – множество метапеременных системы B.
P1i =  ∘ P1ij, где N = {1, 2, …, n}.
∘ P1ij, где N = {1, 2, …, n}.
P2i =  ∘ P2ik, где M = {1, 2, …, m}.
∘ P2ik, где M = {1, 2, …, m}.
∀i∀j ∃l ∊ N такое, что P1ij = P1e
∀i∀k ∃r ∊ M такое, что P2ik = P2r.
Тогда синхронная композиция двух систем уравнений A и B, где P1 = P11 ⊗ P21, конечна.
Доказательство.
Обозначим через ξ(u, v) = P1u ⊗ P2v , (*)
где u = 1, 2, …, n; v = 1, 2, …, m.
Количество выражений ξ(u, v) конечно. По построении синхронной композиции имеем
ξ(u, v) =  ∘ P1uj ⊗
∘ P1uj ⊗ 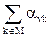 ∘ P2vk =
∘ P2vk =
=  ∘ (P1uj ⊗ P2vk) =
∘ (P1uj ⊗ P2vk) =
= ∘ Pjk, где все Pij входят в множество (*). Таким образом, получается, что система уравнений для синхронной композиции A и B конечна. ■
∘ Pjk, где все Pij входят в множество (*). Таким образом, получается, что система уравнений для синхронной композиции A и B конечна. ■
Верификация
Для верификации с помощью RLTL необходимо наличие модели M на базе RLTL, а также проверяемое относительно нее требование φ, заданное на базе LTL. Для проверки выполнимости в системе заданного требования φ, как и в алгоритме верификации формул логики линейного времени, будет использовано обратное требование ⌉φ. Главным и самым важным отличием предлагаемого алгоритма от алгоритма верификации формул LTL является то, что верификация на базе RLTL более производительная, поскольку не требуется преобразовывать модель и обратное к ней требование в автоматы Бюхи. При этом осуществляется лишь преобразование обратного требования, заданного с помощью LTL, в RLTL-представление. Переход от LTL к RLTL является тривиальным и выполняется по описанным выше правилам и аксиомам в отличие от алгоритмов перехода от LTL к автоматам Бюхи, которые, как сказано в [1], зачастую выдают автоматы Бюхи экспоненциальной сложности относительно длины формулы φ.
 Отметим также, что, если формулировать требования к системе сразу на базе RLTL-нотации, можно в принципе избавиться от всех промежуточных этапов превращения и выполнять процесс верификации сразу после создания модели системы и требований к ней. Указанные выше отличия позволяют существенно повысить производительность процесса верификации по сравнению с верификацией на основе автоматов Бюхи и получить более наглядные представления как модели системы, так и задаваемых требований в виде системы рекурсивных уравнений.
Отметим также, что, если формулировать требования к системе сразу на базе RLTL-нотации, можно в принципе избавиться от всех промежуточных этапов превращения и выполнять процесс верификации сразу после создания модели системы и требований к ней. Указанные выше отличия позволяют существенно повысить производительность процесса верификации по сравнению с верификацией на основе автоматов Бюхи и получить более наглядные представления как модели системы, так и задаваемых требований в виде системы рекурсивных уравнений.
Ключевым процессом в RLTL-верификации, как и в алгоритме верификации формул LTL, является процесс построения синхронной композиции. После того как будет построена композиция двух систем в соответствии с методом, представленным ранее, необходимо выполнить оценку результатов данного процесса. Чтобы исходное требование φ оказалось невыполнимым для модели M, достаточно найти любую ветку вычислительного процесса M, на которой выполняется обратное требование ⌉φ. Если такая ветка существует, она и будет искомым контрпримером. Обратное требование ⌉φ выполнимо для композиции M⊗⌉φ на некотором ее вычислительном пути тогда и только тогда, когда в M⊗⌉φ присутствуют все уравнения из ⌉φ.
Пример 2. Верификация модели.
Дано.
Модель системы (M):
FA1 = a ∘ FA1 + b ∘ FA2,
FA2 = c ∘ FA1.
Проверяемое требование (φ) LTL:
φ = Fc – когда-нибудь наступит «c».
Обратное требование (⌉φ) LTL:
⌉φ = G⌉c – всегда будет «⌉c».
Обратное требование (⌉φ) RLTL:
F⌉B1 = ⌉c ∘ F⌉B1.
Решение.
Построение синхронной композиции M⊗⌉φ:
P1 = FA1⊗F⌉B1 =
=(a⊗⌉c) ∘ (FA1⊗F⌉B1) + (b⊗⌉c) ∘ (FA2⊗F⌉B1) =
=(a⊗(∆\c)) ∘ (FA1⊗F⌉B1) +
+(b⊗(∆\c)) ∘ (FA2⊗F⌉B1) =
=a ∘ (FA1⊗F⌉B1) + b ∘ (FA2⊗F⌉B1) = a ∘ P1+ b ∘ P2.
P2 = FA2⊗F⌉B1 = (c⊗⌉c) ∘ (FA1⊗F⌉B1) =
= ⊥ ∘ FA1⊗F⌉B1 = ⊥.
Конечная синхронная композиция:
P1 = a ∘ P1+ b ∘ P2,
P2 = ⊥.
Результат: P1 = a ∘ P1.
Проверяемое свойство ⌉φ выполняется на M, поскольку в M⊗⌉S в полной мере было реализовано свойство ⌉φ, а именно, его уравнение на одном из путей вычислительного процесса. Из этого следует, что на этом пути не реализуется φ. Значит, путь P1 → a → P1 → a → P1 … → a → P1 является контрпримером.
Рассмотрим более содержательный пример, в котором будет выполняться проверка работы дымового извещателя. Для наглядности на рисунке 3 представлена его модель в виде автомата Бюхи, где a – режим готовности; b – срабатывание датчика дыма; с – опрос соседних датчиков; d – режим тревоги.
Модель дымового извещателя на базе нотации RLTL будет иметь следующий вид:
FA1 = a ∘ FA1 + b ∘ FA2,
FA2 = c ∘ FA3,
FA3 = d ∘ FA4 + a ∘ FA1,
FA4 = d ∘ FA4 + a ∘ FA1.
Проверяемое требование (φ) LTL: φ = = GF(b→Xc) – всегда, в случае наступления в будущем в некоторый момент времени события b, на следующем шаге будет выполнено событие с.
Обратное требование (⌉φ) LTL: ⌉φ = FG(b ∧ ∧ X⌉c) – когда-нибудь наступит такой момент, что всегда будет наступать b на текущем шаге и на следующем шаге будет ⌉с.
Обратное требование (⌉φ) RLTL:
FB1 = b ∘ FB3 + ∆ ∘ FB1,
FB2 = b ∘ FB3,
FB3 = ⌉c ∘ FB2.
Построение синхронной композиции M⊗⌉φ:
P1 = FA1⊗FB1 = (a⊗b) ∘ (FA1⊗FB3) + (b⊗b) ∘ (FA2⊗FB3) +
+ (a⊗∆) ∘ (FA1⊗FB1) + (b⊗∆) ∘ (FA2⊗FB1) =
= ⊥ ∘ (FA1⊗FB3) + b ∘ (FA2⊗FB3) + a ∘ (FA1⊗FB1) +
+ b ∘ (FA2⊗FB1) =
= b ∘ (FA2⊗FB3) + a ∘ (FA1⊗FB1) + b ∘ (FA2⊗FB1) =
= b ∘ P2 + a ∘ P1+ b ∘ P3.
P2 = (FA2⊗FB3) = (c⊗⌉c) ∘ (FA3⊗FB2) = ⊥ ∘ (FA3⊗FB2) = ⊥.
P3 = (FA2⊗FB1) = (c⊗b) ∘ (FA3⊗FB3) +
+ (c⊗∆) ∘ (FA3⊗FB1) =
= ⊥ ∘ (FA3⊗FB3) + c ∘ (FA3⊗FB1) =
= c ∘ (FA3⊗FB1) = c ∘ P4.
P4 = (FA3⊗FB1) = (d⊗b) ∘ (FA4⊗FB3) +
+ (d⊗∆) ∘ (FA4⊗FB1) + (a⊗b) ∘ (FA1⊗FB3) +
+ (a⊗∆) ∘ (FA1⊗FB1) =
= ⊥ ∘ (FA4⊗FB3) + d ∘ (FA4⊗FB1) + ⊥ ∘ (FA1⊗FB3) +
+ a ∘ (FA1⊗FB1) = d ∘ (FA4⊗FB1) + a ∘ (FA1⊗FB1) =
= d ∘ P5 + a ∘ P1.
P5 = (FA4⊗FB1) = (d⊗b) ∘ (FA4⊗FB3) +
+ (d⊗∆) ∘ (FA4⊗FB1) + (a⊗b) ∘ (FA1⊗FB3) +
+ (a⊗∆) ∘ (FA1⊗FB1) =
= ⊥ ∘ (FA4⊗FB3) + d ∘ (FA4⊗FB1) + ⊥ ∘ (FA1⊗FB3) +
+ a ∘ (FA1⊗FB1) = d ∘ P5 + a ∘ P1.
Конечная синхронная композиция:
P1 = FA1⊗FB1 = b ∘ ⊥ + a ∘ (FA1⊗FB1) + b ∘ (FA2⊗FB1) =
= a ∘ P1 + b ∘ P3.
P3 = (FA2⊗FB1) = c ∘ (FA3⊗FB1) = c ∘ P4.
P4 = (FA3⊗FB1) = d ∘ (FA4⊗FB1) + a ∘ (FA1⊗FB1) =
= d ∘ P5 + a ∘ P1.
P5 = (FA4⊗FB1) = d ∘ (FA4⊗FB1) + a ∘ (FA1⊗FB1) =
= d ∘ P5 + a ∘ P1.
Результат. Проверяемое свойство ⌉φ не выполняется на M, поскольку в композиции M⊗⌉S присутствуют не все уравнения из ⌉φ, а именно, нет уравнений FB2 и FB3. Таким образом, исходное требование φ выполнимо на M.
Заключение
В статье предложен и подробно рассмотрен новый алгоритм верификации для метода Model Checking на базе нотации RLTL для верификации формул логики линейного времени. Данный алгоритм во многом схож с алгоритмом верификации формул LTL, поскольку использует аналогичные принципы и подход к решению задачи верификации. Однако он имеет особенность – позволяет сократить число подготовительных этапов, необходимых для верификации, тем самым способствуя повышению производительности метода.
Работа предложенного алгоритма подробно рассмотрена на конкретных примерах с описанием всех этапов и их теоретической базы. Авторы считают, что он может выступить в качестве более производительной альтернативы существующему, а RLTL-нотация может использоваться в качестве основной структуры данных, на базе которой будут задаваться как модели верифицируемых систем, так и требования к ним. В целом же такой подход должен способствовать общему повышению быстродействия метода Model Checking за счет снижения сложности алгоритма верификации и использования единой структуры данных.
Литература
1. Карпов Ю.Г. Model Checking. Верификация параллельных и распределенных программных систем. СПб: БХВ-Петербург, 2010. 552 с.
2. Кораблин Ю.П. Семантика языков распределенного программирования; [под ред. В.П. Кутепова]. М.: Изд-во МЭИ, 1996. 102 с.
3. Kroger F., Merz S. Temporal logic and state systems. Springer, 2008, 436 p.
4. Manna Z., Pnueli A. The temporal logic of reactive and concurrent systems: specification. Springer, 1992, 427 p.
5. Кларк Э.М., Грамберг О., Пелед Д. Верификация моделей программ. Model Checking. М.: Изд-во МЦНМО, 2002. 416 с.
6. Gerard J. Holzman. An analysis of bitstate hashing. Proc. 15th Int. Conf. on Protocol Specification, Testing, and Verification, 1998, pp. 301–314.
7. Ernst-Rudiger Olderog, Krzysztof R. Apt. Fairness in parallel programs: the transformational approach. ACM Trans. Program. Lang. Syst., 1988, vol. 10, no. 3, pp. 420–455.
8. Шипов А.А., Кораблин Ю.П. Построение моделей систем на базе эквациональной характеристики формул LTL // Программные продукты и системы. 2017. № 1. С. 61–66.
9. Шипов А.А., Кораблин Ю.П. Эквациональная характеристика формул LTL // Программные продукты и системы. 2015. № 4. С. 175–179.





 ∘ P1ij, где N = {1, 2, …, n}.
∘ P1ij, где N = {1, 2, …, n}. ∘ P2ik, где M = {1, 2, …, m}.
∘ P2ik, где M = {1, 2, …, m}. ∘ P1uj ⊗
∘ P1uj ⊗ 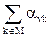 ∘ P2vk =
∘ P2vk = ∘ (P1uj ⊗ P2vk) =
∘ (P1uj ⊗ P2vk) =
