Интеллектуальные функции корабельных тренажеров и пути их реализации
| Шилов К.Ю. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Анализ состояния современного тренажеростроения и тенденций его развития показывает, что основным направлением этого развития будет увеличение интеллектуальных функций процесса обучения, реализованных на основе новых информационных технологий. Поскольку рабочее место оператора является точной копией реального рабочего места и дается разработчикам тренажера в готовом виде, наращивать интеллектуальные возможности тренажера нужно в рамках рабочего места руководителя обучения, которое должно предоставлять обучающему возможность управлять процессом подготовки по показателям уровня обученности [1]. В качестве показателей уровня обученности корабельных операторов наиболее целесообразно применять безошибочность и время выполнения операций управления, которые можно легко интерпретировать на любую шкалу оценок [2]. Рассмотрим один из возможных подходов к формализации ошибок оператора при отработке навыков управления на тренажере, который базируется на известном методе «ветвей и границ» [3]. Если разработанную ЦКБ-проектантом инструкцию по управлению корабельными техническими средствами (КТС) взять за эталон, то отклонения от нее при обучении оператора и будут его ошибками. В математическом плане постановка задачи сводится ко взаимно однозначному соответствию (биекции) двух множеств: f: A®B, где A=a1,a2,…,am – цепочка эталонной структуры; В=b1,b2,…,bn – цепочка реальной структуры; m и n – число операций в А и В. На первый взгляд кажется, что m=n, но при отработке оператора имеют место ошибки типа пропуска (mn) операций. Тогда обратная функция f-–1: A®B становится не всюду определенной, и взаимно однозначное соответствие нарушается. Определим условие существования функции f, которое назовем условием строгого следования: для любых пар операций (аi1, аi2)ÎА и (bj1, bj2)ÎВ, для которых f(аi1)=bj1; f(аi2)=bj2 при условии i1 Если оператор при управлении КТС на тренажере не допускает ошибок, тогда очевидно В=А(m=n, аi=bi, i= Если ошибки есть, то множество операций А и В необходимо сгруппировать на чередующиеся подмножества совпадающих и несовпадающих операций. Для обоснования дальнейших рассуждений введем понятия индикатора совпадений (ИС) и индикатора несовпадений (ИН) [4]. ИС – пара совпадающих подмножеств (аi, аi+1,…,аi+l)ÎА и (bj,bj+1,…,bj+l)ÎВ, ограниченная несовпадающими операциями слева (аi-1¹bj-1) и справа (аi+l+1¹bj+l+l), или началом и концом множеств А и В. Длина индикатора совпадений l=dИС. ИН – пара несовпадающих подмножеств (аi, аi+1,…,аi+v)ÎА и (bj,bj+1,…,bj+w)ÎВ, ограниченная совпадающими операциями слева (аi-1=bj-1) и справа (аi+v+1=bj+w+1) или началом и концом множеств А и В. Величина m(v,w) называется длиной ИН=dИН. Очевидно, что границами ИН будут: левая – между парами совпадающих и несовпадающих операций; правая – между парами несовпадающих и совпадающих операций. Уточним понятие ошибки оператора при управлении КТС: пропуск к операций (v=к; w=0); добавление к операций (v=0; w=к); перестановка к операций (v=к; w=к); замена к операций другими операциями (v=к1; w=к2). Информация о видах ошибок содержится в ИН. Предположим, что G – множество вариантов разбиения подмножеств А и В на чередующиеся Таким образом, вариант g1ÎG является предпочтительным, если он выявляет такие ИН, для которых
где Процесс генерации вариантов giÎG в F-сети представляется узлами (вершинами), которые соответствуют ИС, и дугами, которые соответствуют ИН. Истоку сети соответствует первый ИС в сравниваемых подмножествах А и В. Если а1¹b1, то узел, соответствующий истоку, является фиктивным. Каждому узлу сети (кроме истока) соответствует единственный путь, состоящий из дуг, ведущих от истока в этот узел. Длина пути является суммой длин ИН, соответствующих дугам, из которых образован путь. Определение функциональной сети (F-сети) и ее описательные возможности приведены в [1]. Проиллюстрируем сказанное на примере фрагмента алгоритма по пуску насоса оператором, находящимся на пульте управления КТС. Содержание эталонного и реального фрагментов и их символьное представление показаны в таблице. Таблица
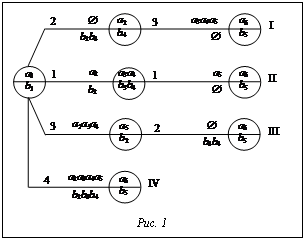
В виде F-сети данный пример будет выглядеть так, как изображено на рисунке 1. Анализ сети показывает, что имеется 4 варианта разбиения подмножеств на чередующиеся ИС и ИН. ИС (узлы сети) для каждого из путей: 1) а1=b1; a2=b4; a6=b5; (ИС: a3=b3 и a4=b4 исключены, так как они одновременно входят в вариант II); 2) а1=b1; a3а4=b3b4; a6=b5; 3) а1=b1; a5=b2; a6=b5; 4) а1=b1; a6=b5. Арабские цифры отражают длины ИН. В соответствии с выражением (1) предпочтительным является второй вариант сравнения, для которого общее число ошибок равно двум. Ветви, выходящие из каждого узла, соответствуют различным ИН, имеющим общую левую границу (аi-1=bj-1, аi¹bj), но различные правые границы. Это связано с тем, что алгоритмы управления состоят из разных операций и к ним не могут быть применены формальные алгебраические преобразования (законы поглощения, универсального множества и т.п.). В противном случае реальный алгоритм может сильно отличаться от идеального. Для нахождения всех правых границ надо образовать множество: Г=(аi,аi+1,…,аi+n)´(bj,bj+1,…, bj+n) и из него выбрать такие пары (ар,аr)ÎГ, для которых ар=аr. Величина v является глубиной перебора v£max(m,n). С учетом специфики алгоритмов управления КТС введем следующие ограничения. · Ограничим глубину перебора v величиной dИНД – допустимой длиной ИН, очевидно, зависящей от числа видов ошибок оператора, которые необходимо идентифицировать. Если при сравнении подмножеств А и В отсутствуют ИН длиной dИН£dИНД, то эти подмножества будем выводить на экран ПЭВМ рабочего места руководителя обучением для визуального анализа. · Декомпозируем сравниваемые подмножества А и В на участки детального анализа, отделенные друг от друга индикаторами совпадений длиной dИС³dИСД, где dИСД – допустимая длина ИС. Введение таких участков позволяет заменить предпочтительный по критерию (1) вариант сравнения подмножеств А и В в целом последовательным поиском варианта в каждом из участков детального анализа. · Назовем совокупность стоящих подряд ИН длиной dИН£dИНД, ограниченную слева и справа индикаторами совпадений длиной dИС³dИСД, совокупностью несовпадений (СН) (рис. 2) [4]. Количество ИН и СН назовем мощностью подмножества СН и обозначим МСН. В соответствии с методом ветвей и границ [3] ветвление нецелесообразно: - если МСН>МСНД, где МСНД – допустимая мощность СН; при отсутствии СН мощностью МСН£МСНД сравниваемые подмножества выводятся на экран ПЭВМ руководителя обучением для визуального анализа; - если сумма длин ИН, найденных на i-м шаге ветвления, больше (или равна) аналогичной суммы для СН, найденной на предыдущих шагах ветвления. Отсечение неперспективных вариантов, характерное для метода ветвей и границ, в данном случае не происходит, так как это приведет к потере части операций в алгоритме управления КТС. Операция отсечения заменена операцией упорядоченного перебора вариантов. В F-сети используются следующие узлы (вершины) [1]: - допускающие ветвление, ИС длиной dИС - не допускающие ветвления, ИС длиной dИС - исчерпывающие мощность СН, ИС длиной dИС - конечные узлы (вершины) – ИС длиной dИС³dИСД. Смысл упорядоченного перебора вариантов заключается в следующем. Двигаясь по F-сети, сначала находится вершина 4, путь к которой имеет наименьшую длину. Далее анализируются пути к узлам (вершинам) типов 2, 3 и 1, которые не короче наименьшего по длине пути к узлу типа 4, уже найденного на предыдущих шагах ветвления. Возможными путями на сети могут быть варианты: 4,2,3,1; 4,3,2,1; 4,1,2,3; 4,1,3,2; 4,2,1,3 и 4,3,1,2.
Таким образом, модифицированный алгоритм поиска ошибок оператора (без отсечения путей на сети), основанный на методе ветвей и границ, будет состоять из следующих основных операций: 1) совместить начальные символы подмножеств А и В (i=1, j=1); 2) если i>m, j>n, то перейти к шагу 18, иначе – к шагу 3; 3) если аi=bj, то перейти к шагу 4, иначе – к 5; 4) установить i=i+1, j=j+1 и перейти к шагу 2; 5) найти ИН; 6) если dИН£dИНД, то перейти к шагу 7, иначе – к шагу 13; 7) если ИН входит в СН, то перейти к шагу 8, иначе – к шагу 5; 8) найти ИС; 9) если dИС³dИСД, то перейти к шагу 10, иначе – к шагу 11; 10) зарегистрировать найденную СН (номера мест левых и правых границ ИН, входящих в СН) и перейти к шагу 5; 11) прибавить 1 к счетчику МСН; 12) если МСН<МСНД, то перейти к шагу 5, иначе – к шагу 13; 13) вычесть 1 из показаний счетчика МСН; 14) если МСН=0, то перейти к шагу 15, иначе – к шагу 5; 15) если на шаге 10 регистрировалась информация о СН, то перейти к шагу 16, иначе – к шагу 17; 16) распечатать результаты анализа; 17) распечатать подмножества А и В для визуального анализа; 18) конец алгоритма. Предлагаемый подход реализован при разработке рабочего места руководителя обучения конкретного тренажера и апробирован в процессе обучения операторов КТС. Список литературы 1. Кобзев В.В., Шилов К.Ю. Методы создания технических средств обучения корабельных операторов. – СПб.: Наука, 2005. 2. Шилов К.Ю., Бобрович В.Ю., Кобзев В.В. Выбор и обоснование показателей уровня обученности операторов в процессе тренажерной подготовки. // Системы управления и обработки информации. – СПб.: ФНПЦ «НПО «Аврора». - 2005. - Вып. 10. - С. 72. 3. Захаров И.Г. Обоснование выбора. Теория практики. - СПб.: Судостроение, - 2006. 4. Ротштейн А.П., Кузнецов П.Д. Проектирование бездефектных человеко-машинных технологий. - Киев: Техника, 1992. |
http://swsys.ru/index.php?id=434&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Гибридная система поиска решений на основе временных продукционных правил
- Информационная поддежка технического обеспечения кораблей при первой операции флота
- Оценка защищенности информации от несанкционированного доступа при помощи имитационной модели системы защиты информации
- Методы и средства моделирования wormhole сетей передачи данных
- Место XML-технологий в среде современных информационных технологий

 ).
). ИС и ИН. В теоретическом плане оператор может ошибаться на каждой операции управления. На практике же наиболее предпочтительным является вариант giÎG, для которого требуется наименьшее число операций по устранению ошибок в подмножестве В, что совпадает с целевой установкой обучения оператора на тренажере.
ИС и ИН. В теоретическом плане оператор может ошибаться на каждой операции управления. На практике же наиболее предпочтительным является вариант giÎG, для которого требуется наименьшее число операций по устранению ошибок в подмножестве В, что совпадает с целевой установкой обучения оператора на тренажере. , (1)
, (1) – общее число операций в подмножестве В, выполненных с ошибками, при варианте сравнения giÎG;
– общее число операций в подмножестве В, выполненных с ошибками, при варианте сравнения giÎG;  – длина i-го ИН в варианте giÎG; Ni – количество ИН в варианте giÎG.
– длина i-го ИН в варианте giÎG; Ni – количество ИН в варианте giÎG.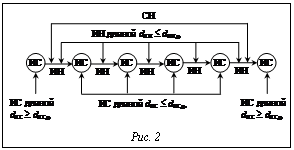 Если к пути добавляется один узел (вершина), то показания счетчика мощности МСН увеличиваются на единицу; если совершается возврат по петле или циклу к предыдущему узлу сети, то показания счетчика МСН уменьшаются на единицу. Началу сети (корню) соответствует МСН=0.
Если к пути добавляется один узел (вершина), то показания счетчика мощности МСН увеличиваются на единицу; если совершается возврат по петле или циклу к предыдущему узлу сети, то показания счетчика МСН уменьшаются на единицу. Началу сети (корню) соответствует МСН=0.