Принятие оптимальных решений на основе ситуационного анализа аномальных состояний системы
| Ивашкин Ю.А. (ivashkin@msaab.ru) - Московский государственный университет прикладной биотехнологии, доктор технических наук, Беляева М.А. (Belyaevamar@mail.ru) - Государственный университет управления (профессор), Москва, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Предлагаемый подход к моделированию и идентификации состояния больших систем основан [1,2] на формализованном описании в матричной форме влияния различных факторов на критерий достижения цели, выражаемый многомерной суммой взвешенных нормированных отклонений параметров состояния системы от заданных значений. Эффективность функционирования системы любой физической и социальной природы описывается вектором параметров Y={y1,…,ym} или критерием Q(y1,…,ym) оценки состояния системы (качество продукции, производительность, себестоимость и т.п.). Компоненты вектора Y в общем случае являются функциями характеристик входных потоков G={g1,…,gr} и параметров состояния системы X={х1,…,хn}, которые, в свою очередь, зависят от факторов возмущения V={v1,…,vq} и управляющих воздействий U={u1,…,up}. Задачей системного анализа сложного объекта является параметрическое описание происходящих процессов, качества сырья, промежуточного и конечного продуктов, технологических режимов и оборудования и нахождение математических зависимостей между ними для последующей многокритериальной оптимизации и принятия оптимальных решений. С этой целью строится матричная структурно-параметрическая модель системы [1] (см. рис.).
Недиагональные клетки описывают характеристики связей и взаимодействия между элементами и блоками технологической системы, определяемые методами факторного анализа, планирования эксперимента и экспертных оценок. Таким образом, клеточная матрица представляет полное описание структуры и характеристик связей между параметрами и факторами, определяющими функционирование любого технологического процесса или комплекса. Критерий оценки состояния системы можно записать [2] в виде аддитивно-мультипликативной свертки
где При Для оценки групповых и индивидуальных весовых коэффициентов формируется таблица экспертных оценок функционала по схеме полного или дробного факторного эксперимента с последующим вычислением оценок линейных эффектов влияния на функционал по формулам
где zik – значение i-го группового показателя в k-м опыте; zijk – значение j-й переменной i-й группы в k-м эксперименте; Qk – значение функционала в k-м эксперименте. Детализация параметрических описаний объекта в виде клеточной матрицы определяется конкретной задачей идентификации и моделирования системы, а также характером априорных данных о качественных и количественных показателях влияния и взаимодействия между ее элементами. Коэффициенты связей в виде сопоставимых количественных характеристик могут быть найдены известными методами в зависимости от степени априорных представлений о природе вещей. На основе статистических данных о состоянии системы и среды в виде массива xkj;
где Характер связей между коррелируемыми факторами определяется коэффициентами линейной множественной регрессии
с коэффициентами связи Pij j-го фактора c i-м. Для сопоставимой оценки отклонений и связей параметров различной физической природы и размерности формируется матрица безразмерных характеристик
где Dxi0, Dxj0 – допустимые отклонения от нормы. По найденной матрице характеристик взаимосвязей Cij;
При этом общий алгоритм принятия решений сводится к накоплению базы знаний в виде структурно-параметрической модели связей и к решению задач анализа причин аномальных состояний и принятию оптимальных решений в различных сферах деятельности. Структурно-параметрическая оптимизация сводится к нахождению оптимальных значений параметров состояния системы по критериям P(x), Φ(x) и Ψ(x) минимального отклонения от заданной или желаемой структуры показателей на разных уровнях анализа и управления:
где хij0, xij – значения j-й переменной состояния системы i-го блока на первом уровне иерархической структуры в желаемой и текущей ситуациях;
где blj0, blj – удельный вес l-го компонента второго уровня иерархии в j-й интегральной характеристике первого уровня в заданном и достигаемом состояниях системы; akl0, akl – удельное содержание k-го элемента третьего уровня в l-м компоненте второго уровня иерархии. Оптимизация состояния системы с минимизацией отклонения от заданной исходной структуры показателей состояния по предлагаемым критериям осуществляется методом покоординатного поиска в заданных интервалах варьирования переменных с прогнозированием конечного состояния по вышеупомянутому алгоритму [1,2] идентификации и прогнозирования на основе ситуационной модели. Список литературы 1. Ивашкин Ю.А. Структурно-параметрические модели и алгоритмы идентификации аномальных состояний технологической системы. // Вестн. Росс. акад. диалектно-системных исследований. - М.: РХТУ им. Д.И. Менделеева, 1998. - Вып. 2. - С.18-28. 2. Ивашкин Ю.А. Структурно-параметрическое моделирование и идентификация аномальных ситуаций в сложных технологических системах // Проблемы управления.- 2004. -№ 3. - С. 39-43. |
http://swsys.ru/index.php?id=435&lang=.docs&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Кросс-система автоматизации разработки программного обеспечения на базе языка высокого уровня Рада
- Исследовательское проектирование в кораблестроении на основе гибридных экспертных систем
- Методы поисковой адаптации на основе механизмов генетики, самообучения и самоорганизации
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Информационно-вычислительный комплекс по применению мембран в биотехнологии

 Каждый диагональный блок матрицы описывает параметры состояния отдельных функциональных подсистем и их цели и может быть разделен на более мелкие составные элементы или подсистемы с описанием конкретных факторов и их влияния на элементы и подсистемы.
Каждый диагональный блок матрицы описывает параметры состояния отдельных функциональных подсистем и их цели и может быть разделен на более мелкие составные элементы или подсистемы с описанием конкретных факторов и их влияния на элементы и подсистемы.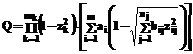 , (1)
, (1) и bij – относительное отклонение j-го фактора i-го блока системы и его весовой коэффициент;
и bij – относительное отклонение j-го фактора i-го блока системы и его весовой коэффициент;  – фактическое и желаемое значение параметра состояния;
– фактическое и желаемое значение параметра состояния;  – допустимое отклонение параметра от желаемого значения; ai – коэффициент значимости i-й группы факторов; zk – отклонение k-го фактора критической группы, определяющей неприемлемость качественного состояния системы.
– допустимое отклонение параметра от желаемого значения; ai – коэффициент значимости i-й группы факторов; zk – отклонение k-го фактора критической группы, определяющей неприемлемость качественного состояния системы. и
и  функционал (1) изменяется от 1 до 0, соответственно от эталонного состояния до его граничного допустимого значения, и обращается в нуль при выходе любого параметра критической группы за предельно допустимый уровень.
функционал (1) изменяется от 1 до 0, соответственно от эталонного состояния до его граничного допустимого значения, и обращается в нуль при выходе любого параметра критической группы за предельно допустимый уровень.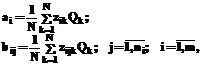 (2)
(2)
 , где xkj – значение j-го фактора в k-м опыте, составляется матрица коэффициентов корреляции
, где xkj – значение j-го фактора в k-м опыте, составляется матрица коэффициентов корреляции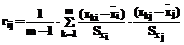 , (3)
, (3) – средние значения i-го и j-го факторов;
– средние значения i-го и j-го факторов;  – среднеквадратичные отклонения соответствующих факторов.
– среднеквадратичные отклонения соответствующих факторов. (4)
(4) , (5)
, (5)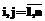 и вектору текущих отклонений Dx1, …, Dxn путем умножения ||Cij ||n на диагональную матрицу вектора изменения параметров состояния ||Dхjdjk|| формируется ситуационная матрица (6), описывающая разложение Dхi,
и вектору текущих отклонений Dx1, …, Dxn путем умножения ||Cij ||n на диагональную матрицу вектора изменения параметров состояния ||Dхjdjk|| формируется ситуационная матрица (6), описывающая разложение Dхi,  по всем координатам множества {C} и определяющая формальную процедуру идентификации аномального состояния системы [1]:
по всем координатам множества {C} и определяющая формальную процедуру идентификации аномального состояния системы [1]: . (6)
. (6) , (7)
, (7) , (8)
, (8) , (9)
, (9)