В настоящее время существуют методологии извлечения из эксперта знаний о динамических свойствах ситуаций (причинно-следственные отношения), а для фиксации этих знаний используется модель их представления в виде так называемой когнитивной карты. Методы анализа динамических ситуаций на основе когнитивных карт дают хорошо интерпретируемые результаты моделирования (прогнозы развития ситуаций и стратегии перевода ситуации в целевое состояние) для небольших когнитивных карт. Для оценки прогнозов развития ситуации и решений по управлению ею могут быть использованы статические модели оценивания состояния ситуации. Методология когнитивного моделирования основана на построении субъективной модели ситуации, отражающей знания субъекта о законах ее развития. Субъективная модель ситуации строится экспертным путем и представляется в виде ориентированного знакового графа (когнитивной карты), в котором вершины – это факторы ситуации, а взвешенные дуги – причинно-следственные отношения, вес которых отражает силу влияния факторов ситуации. Направленным дугам графа приписывается знак «+» или «–», то есть они могут быть положительными или отрицательными. Положительная связь означает, что увеличение значения фактора-причины приводит к увеличению значения фактора-следствия, а отрицательная – что увеличение значения фактора-причины приводит к уменьшению значения фактора-следствия. Задачи, решаемые с помощью когнитивных карт, заключаются в нахождении и оценивании влияний факторов ситуации и в получении на основе вычисленных влияний прогнозов развития ситуации. В настоящее время для вычисления влияний и прогнозов развития ситуации широкое применение находят нечеткие когнитивные карты (НКК).
Понятие НКК было предложено Б. Коско в 1986 г. [1] и используется в моделировании при- чинных взаимосвязей, выявленных между понятиями некоторой области [2]. НКК представляет собой нечеткий ориентированный граф с обратной связью, узлы которого являются нечеткими множествами. Направленные ребра графа отражают причинно-следственные связи между понятиями и численно характеризуют степень влияния (вес) связываемых понятий. Сила влияния между факторами, в отличие от простых когнитивных карт, задается с помощью лингвистических значений, выбранных из упорядоченного множества возможных сил влияний. Значения факторов, их приращения также задаются в лингвистическом виде и выбираются из упорядоченных множеств возможных значений фактора и его возможных приращений – шкал факторов и шкал приращений.
НКК объединяют в себе свойства нечетких систем и нейронных сетей. Использование НКК в качестве средства моделирования систем позволяет наглядно отобразить структуру взаимосвязей анализируемой системы и облегчает интерпретацию причинно-следственных связей между концептами. С точки зрения искусственного интеллекта НКК являются нейронными сетями, обучаемыми с учителем: чем больше данных доступно для моделирования задачи, тем более адаптивной является НКК в плане развития и выработки подходящего решения. Таким образом, НКК хорошо подходят для задач поиска решения на множестве альтернатив. Рассмотрим некоторые области применения данной технологии.
С этой областью связаны работы по интеграции моделей прогноза и оценивания неструктурированных ситуаций на основе подходов когнитивного моделирования. Такие модели охватывают все этапы процесса поддержки принятия решений (от анализа ситуации до выбора лучшей альтернативы) и предназначены для поддержки деятельности аналитиков в условиях неопределенности.
В качестве примера можно привести интегрированную модель поддержки принятия решений [3]. Модель поддержки принятия решений в слабо структурированных динамических ситуациях основана на интеграции нечеткой иерархической модели оценивания и нечеткой когнитивной модели ситуации. Интегрированная модель в отличие от каждой из составляющих ее моделей поддерживает все этапы процесса поддержки принятия решений. Анализ ситуации основывается на декомпозиции цели, определенной экспертом, и структурно-функциональной декомпозиции ситуации, позволяющей с системных позиций описать поведение неструктурированной ситуации – ее динамики. Конструирование (генерация) решений – альтернатив осуществляется с помощью когнитивной модели; выбор лучшего решения основан на оценивании прогнозов развития ситуации, полученных с помощью когнитивной модели в иерархической модели оценивания. В интегрированной модели множество альтернатив нефиксированное, есть возможность конструирования альтернативы и оперативного получения ее оценки относительно достижения генеральной цели.
Таким образом, иерархическая модель оценивания альтернатив управления ситуацией и динамическая когнитивная модель ситуации описывают одну и ту же наблюдаемую ситуацию, но в разных аспектах. Модель оценивания описывает ситуацию с точки зрения цели управления ситуацией, степень достижения которой выражается через предпочтения эксперта относительно критериев, выраженных с помощью их весов и конкретных значений множества листовых критериев, представленных в некоторой шкале. В динамической модели ситуации описываются изменения значений факторов во времени безотносительно их важности для достижения поставленной цели. Эта модель качественно описывает динамику развития ситуации, представленную в качественных шкалах факторов ситуации. Для интеграции этих моделей ситуации не- обходимо обеспечить, во-первых, пересечение факторов ситуации, описываемой в каждой из перечисленных моделей, во-вторых, отображение значений факторов ситуации, полученной в когнитивной модели, в значения листовых критериев модели оценивания. Проблема обеспечения пересечения факторов когнитивной карты и листовых критериев иерархии оценивания решается путем согласования методологий построения иерархической модели оценивания и когнитивной карты.
Интегрированная модель позволяет оценивать изменения текущего состояния ситуации, что дает возможность использовать ее в системах мониторинга состояния ситуации. Разработанная интегрированная модель поддержки принятия решений может служить теоретической основой для разработки компьютерной системы поддержки принятия решений в неструктурированных ситуациях, основанной на моделировании знаний и предпочтений эксперта.
 Подобные подходы используются в системах бизнес-аналитики для экономики знаний на основе интеллектуальных систем поддержки принятия решений, использующих когнитивные методы анализа сознания людей, вовлеченных в эти процессы, а также тестирование качества ЛПР по их мозговой активности, для параметрической настройки интеллектуальных систем поддержки принятия решений (рис. 1).
Подобные подходы используются в системах бизнес-аналитики для экономики знаний на основе интеллектуальных систем поддержки принятия решений, использующих когнитивные методы анализа сознания людей, вовлеченных в эти процессы, а также тестирование качества ЛПР по их мозговой активности, для параметрической настройки интеллектуальных систем поддержки принятия решений (рис. 1).
Когнитивные методы принятия решений в поведенческой экономике
Имеется большое количество работ по поведенческой экономике, в которых используются классические модели на основе рациональности. ЛПР демонстрируют ограниченную рациональность и полную иррациональность, что затрудняет прогнозирование и принятие решений в ситуациях неопределенности. Поведенческая экономика – это область экономики, которая изучает влияние социальных, когнитивных и эмоциональных факторов на принятие экономических решений. Она тесно взаимосвязана с когнитивной и экспериментальной экономиками [4]. В этих областях научных исследований используются методы нейрофизиологии, психологии, лингвистики, антропологии, а также весь аппарат современных компьютерных наук вплоть до робототехники и моделирования мозга на суперкомпьютере. Все эти направления так или иначе связаны с представлением знаний в мозге человека.
Нерациональность поведения человека не раз подтверждалась экспериментально. Нобелевский лауреат Дениэл Канеман выдвинул предположение о существовании двух эволюционно и структурно различающихся систем, обусловливающих при- нятие решений: a) быстрой, автоматической, или бессознательной (Система 1), б) медленной, целенаправленной, произвольной (Система 2). C некоторым приближением классический условный рефлекс и привыкание могут быть объединены в единую автоматическую Систему 1, тогда как целенаправленное поведение (реализуемое в том числе и через инструментальные рефлексы) в таком случае будет являться частью произвольной Системы 2.
В настоящее время многочисленные нейроэкономические исследования посвящены изучению взаимодействия рациональной и эмоциональной систем в рамках дуализма Канемана. Среди наиболее часто используемых экспериментальных моделей можно назвать игру «Ультиматум», наиболее ярко демонстрирующую возникновение подобного рода конфликтов: двум игрокам необходимо поде- лить между собой определенную сумму денег, например 100 рублей. Один из них первым предла- гает способ дележа, причем он абсолютно свободен в своем решении. Предположим, игрок захочет оставить 80 рублей себе, а 20 рублей отдать своему партнеру по игре. Партнер, которому сделали предложение, оказывается перед выбором: согласиться или не согласиться; однако, если респондент не соглашается, то, по правилам игры, денег не получает никто и игра заканчивается.
Используя метод функциональной магнитно-резонансной томографии (ФМРТ), американский нейробиолог Алан Сенфи показал, что у респондента, которому сделали несправедливое предложение в игре «Ультиматум», наблюдается активация островковой коры (anterior insula), которая, как известно из других нейробиологических иссле- дований, вовлечена в обработку негативной эмоциональной информации и особенно активна при эмоции отвращения. Интересно, что в данном исследовании активность островковой коры была пропорциональна степени несправедливости предложения. Кроме того, наблюдалась активация верхних областей лобной коры (dorsolateral prefrontal cortex, DLPFC) правого полушария и поясной извилины (anterior cingulate cortex) – областей, активация которых наблюдается при запуске когнитивных процессов самоконтроля и при внутренних конфликтах соответственно. Особого внимания заслуживает тот факт, что по соотношению активности островковой и лобной коры (DLPFC) можно предсказать, будет ли полученное игроком предложение принято или отвергнуто. Если несправедливое предложение отвергалось, наблюдалась более сильная активация островковой коры по сравнению с областью DLPFC, тогда как в случае принятия несправедливого предложения, наоборот, боль- шая активация наблюдалась в DLPFC и меньшая в островковой коре (см. рис. http://www.swsys.ru/uploaded/image/2017_4/2017-4-dop/1.jpg).
Одним из последних методических достижений когнитивных нейронаук стала транскраниальная магнитная стимуляция (transcranial magnetic stimulation, ТМС). ТМС-стимулятор – прибор, который при помощи электромагнитной катушки (конфигурации типа петли Мебиуса для оптимальной фокусировки стимулирующего импульса), располагающейся у поверхности головы, подавляет или активируют работу прилегающих зон мозга. Когда при помощи ТМС временно подавлялась активность DLPFC в правом полушарии, испытуемые принимали несправедливые предложения в игре «Ультиматум» гораздо чаще, чем испытуемые, у которых подавлялась активность DLPFC в левом полушарии.
При создании поведенческой модели принятия решения учитывались эмоции ЛПР (Система 1) и репрезентативность (Система 2). В модели используются нечеткая логика и продукционные правила. Этот подход делает модель принятия решений интуитивно понятной благодаря лингвистическим переменным, формирующим продукционные правила. Еще одно преимущество – универсальность и шкалируемость, получаемая при переходе к моделям с большим число параметров.
На этапе построения модели выделены шесть входных переменных (Service, Offer, DuringEmptions, Money, Cost, EmotionBefor) и две выходные (Expenses, EmotionAfter). Такие переменные, как DuringEmptions, EmotionBefor, Service, EmotionAfter, относятся к Системе 1, а переменные Offer, Money, Cost, Expenses, Service – к Системе 2. Каждая переменная принимает от трех до шести состояний, имеющих соответствующее лингвистическое значение, так, например, первая входная лингвистическая переменная Service имеет терм-множество Т1 = {“bad”, ”good”, ”excellent”}. Соответственно, DuringEmptions T2 = {“bad”, ”okay”, ”good”}, Cost T3 = {“small”, ”normal”, ”huge”} и т.д. Всем значениям переменных ставятся в соответствие интервалы на универсальной шкале. Пример продукционного правила: if (Money is many) and (Cost is normal) and (EmotionBefor is okay) then (EmotionsAfter is good) (Expenses is max).
В модели применяется алгоритм нечеткого вывода Мамдани в среде Fuzzy Toolbox MATLAB [5].
 Этой относительно простой схемы вполне достаточно для выявления основных принципов моделирования принятия решений в неопределенности на основе теории перспектив. В качестве результата моделирования имеем процентные значения выходных переменных на универсальной шкале. Основной интерес с точки зрения анализа полученных результатов представляют поверх- ности нечеткого вывода, позволяющие проанализировать значения выходных переменных при изменении входных. Для примера рассмотрим по- верхность, отражающую зависимость величины расходов или склонности к риску от уровня доходов ЛПР. То есть эта поверхность представляет собой функцию полезности. Изменив названия переменных Системы 2, промоделируем решение ЛПР о количестве чаевых в ресторане в зависимости от количества его доходов (рис. 2, слева).
Этой относительно простой схемы вполне достаточно для выявления основных принципов моделирования принятия решений в неопределенности на основе теории перспектив. В качестве результата моделирования имеем процентные значения выходных переменных на универсальной шкале. Основной интерес с точки зрения анализа полученных результатов представляют поверх- ности нечеткого вывода, позволяющие проанализировать значения выходных переменных при изменении входных. Для примера рассмотрим по- верхность, отражающую зависимость величины расходов или склонности к риску от уровня доходов ЛПР. То есть эта поверхность представляет собой функцию полезности. Изменив названия переменных Системы 2, промоделируем решение ЛПР о количестве чаевых в ресторане в зависимости от количества его доходов (рис. 2, слева).
На рисунке видно, что поверхность нечеткого вывода имеет участки, схожие с функцией полезности, полученной экспериментально, и совпадает с функцией полезности, полученной в работе М. Фридмена, Л. Дж. Сэвиджа «Анализ полезности при выборе среди альтернатив, предполагающих риск» (рис. 2, справа). Но основное достоинство этой модели в том, что при принятии решения учитываются влияние эмоционального центра головного мозга ЛПР, что позволяет смоделировать ограниченную рациональность или полную иррациональность поведения в неопределенности. Например: if (Money is many) and (Service is normal) and (Offer is okay) and (EmotionBefor is angry) then (EmotionsAfter is bad) (Expenses is small) или if (Money is many) and (Service is bad) and (EmotionBefor is happy) then (EmotionsAfter is good) (Expenses is generous). То есть ЛПР может отвергать выгодные предложения или принимать невыгодные под действием эмоций.
Таким образом, созданная модель представляет собой аппроксимацию работы Системы 1 и Системы 2 на универсальных шкалах с использованием продукционных правил [2].
Интегрированная модель поддержки принятия решений
Иерархическая модель оценивания альтернатив управления ситуацией и динамическая когнитивная модель ситуации описывают одну и ту же наблюдаемую ситуацию, но в разных аспектах.
Модель оценивания описывает ситуацию с точки зрения цели управления ситуацией, степень достижения которой выражается через предпочтения эксперта относительно критериев, выраженных с помощью их весов и конкретных значений множества листовых критериев, представленных в некоторой шкале.
В динамической модели ситуации описываются изменения значений факторов во времени безотносительно их важности для достижения поставленной цели. Эта модель качественно описывает динамику развития ситуации, представленную в качественных шкалах факторов ситуации.
Для интеграции этих моделей ситуации необходимо обеспечить, во-первых, пересечение факторов ситуации, описываемой в каждой из перечисленных моделей, во-вторых, отображение значений факторов ситуации, полученной в когнитивной модели, в значения листовых критериев модели оценивания.
Проблему обеспечения пересечения факторов когнитивной карты и листовых критериев иерархии оценивания предлагается решить путем согласования методологий построения иерархической модели оценивания и когнитивной карты.
При построении оценочной иерархии эксперты пользуются методологией декомпозиции цели «сверху вниз», которая позволяет достаточно полно описать проблемную ситуацию, то есть построить системную оценочную модель ситуации, включающую оценки элементов ситуации разных уровней.
Существующая в настоящее время методология построения когнитивных карт ориентирована на построение концептуальных моделей, отражаю- щих наиболее общие законы развития и управ- ления ситуацией. Очевидно, что при такой мето- дологии построения когнитивной карты достичь пересечения факторов когнитивной карты и иерархической модели оценивания будет трудно. В этом случае число листовых критериев иерархии оценивания ситуации будет больше (поскольку иерархическая модель оценивания более конкретна и точна) числа факторов модели когнитивного моделирования.
Для решения проблемы интеграции когнитивной модели и иерархической модели предлагается использовать системную методологию построения когнитивной карты ситуации, рассмотренную в работе [6]. Эта методология основывается на структурно-функциональной декомпозиции ситуации и описании ситуации в двух аспектах: структурном и функциональном. Описание ситуации в структурном аспекте заключается в выделении составных частей наблюдаемой ситуации в виде иерархии «Часть–Целое», áD, Qñ, где D = {di} – множество элементов, характеризующих целое и составные части ситуации; Q – отношение «Часть–Целое», заданное на множестве элементов ситуации D. При структурной декомпозиции определяются основ- ные факторы Fi = {fij} всех элементов ситуации di.
При описании в функциональном аспекте строятся когнитивные карты для каждого элемента ситуации di Î D, которые представляются парой (Fi, Wi), где Fi = {fij} – факторы элемента di; Wi – матрица смежности графа, отражающая знания о законах функционирования элемента ситуации di.
Когнитивные карты (Fi, Wi) элементов ситуации объединяются в когнитивную карту сложной ситуации (F, W), где F = È Fi – множество факторов – факторов ситуации; W – матрица смежности орграфа, описывающая сложную ситуацию и включающая матрицы Wi отдельных элементов ситуации и связи между ними.
Построение когнитивной карты на основе такой методологии дает возможность расширить множество факторов когнитивной модели F до уровня, позволяющего подробно описать ситуацию и приблизиться к уровню описания ситуации в модели иерархического оценивания.
Далее задача эксперта заключается в том, чтобы выделить среди факторов когнитивной модели факторы, близкие по смыслу листовым критериям иерархической модели. Выделяя такие факторы, эксперт определяет подмножество F Ì F факторов когнитивной модели, соответствующих листовым критериям li, i = 1, n.
Например, на рисунке 3 показан результат декомпозиции «Часть–Целое» проблемы защиты интересов личности. Выделены следующие составные части: государство, социум и экономика. Социум включает составные части, определяющие две социальные группы: пенсионеры и рабочие и служащие.
На рисунке 3 в соответствующих блоках перечислены основные признаки составных частей, которые являются факторами в когнитивной карте ситуации.

 Когнитивная карта ситуации показана на рисунке 4. Здесь экспертным способом были определены причинно-следственные отношения между факторами ситуации и веса связей, характеризующие силу влияния.
Когнитивная карта ситуации показана на рисунке 4. Здесь экспертным способом были определены причинно-следственные отношения между факторами ситуации и веса связей, характеризующие силу влияния.
Пересечение факторов когнитивной карты и листовых критериев – это множество Ф, которое включает следующие факторы когнитивной карты: «уровень жизни пенсионеров», «уровень жизни рабочих и служащих», «уровень безработицы», «уровень социального расслоения общества», «уровень преступности», «объем финансирования бесплатной медицины».
Значения относительной важности для альтернатив в модели иерархического оценивания могут быть получены, если заранее задано множество оцениваемых альтернатив.
При интеграции модели иерархического оценивания с моделью когнитивного моделирования альтернативы заранее не могут быть определены. Они строятся в процессе моделирования поведения ситуации с помощью когнитивной модели. Поэтому предлагается построить значения для листовых критериев на основе шкал соответствующих им факторов когнитивной модели.
В общем случае необходимо построить отображение:  , где {xij} – множество значений фактора fi когнитивной модели, заданных на отрезке числовой оси на [0, 1];
, где {xij} – множество значений фактора fi когнитивной модели, заданных на отрезке числовой оси на [0, 1];  – множество значений соответствующего листового критерия lm иерархии,
– множество значений соответствующего листового критерия lm иерархии,  Î [0, 1].
Î [0, 1].
Рассмотрим правила построения отображения  для следующих трех случаев.
для следующих трех случаев.
1. Эксперт определяет взаимно однозначное соответствие листового критерия lm и фактора fi когнитивной модели. Тогда отображение  – тождественная функция, значит, каждое значение шкалы фактора равно значению шкалы критерия, то есть
– тождественная функция, значит, каждое значение шкалы фактора равно значению шкалы критерия, то есть 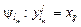 , где j – количество градаций шкалы фактора fi.
, где j – количество градаций шкалы фактора fi.
2. Эксперт определяет соответствие листового критерия и фактора когнитивной модели по смыслу, однако не выполнено правило положительной связи, действующее при построении иерархической модели. То есть реализация критериев, находящихся на нижележащих уровнях, не приводит к снижению возможности реализации критериев, находящихся на вышележащих уровнях. В когнитивной модели могут существовать факторы, близкие по смыслу некоторому критерию, но снижающие возможность реализации критериев вышележащего уровня. Например, в иерархической модели листовым критерием lm может быть критерий «занятость», а близкий к нему по смыслу фактор fi когнитивной модели – «безработица». В таких случаях отображение 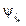 имеет следующий вид:
имеет следующий вид:  , i = 1, j, где j – количество градаций шкалы фактора fi.
, i = 1, j, где j – количество градаций шкалы фактора fi.
3. Экспертом обозначена смысловая близость фактора fi и критерия lm, однако отображение  не может быть определено перечисленными выше способами. В этом случае предлагается построить шкалу критерия lm и каждому значению xij шкалы фактора fi поставить в соответствие значение на шкале критерия lm, то есть
не может быть определено перечисленными выше способами. В этом случае предлагается построить шкалу критерия lm и каждому значению xij шкалы фактора fi поставить в соответствие значение на шкале критерия lm, то есть  .
.
После определения отображения  для всех критериев lm интегрированная модель считается построенной.
для всех критериев lm интегрированная модель считается построенной.
В рассматриваемом примере построим шкалы критериев. Причем для критериев «уровень жиз- ни пенсионеров», «уровень жизни рабочих и служащих», «уровень социального расслоения общества», «уровень преступности» строится тождественное отображение шкал одноименных факторов когнитивной карты в шкалы критериев иерархии. Шкала критерия «занятость населения» строится из шкалы фактора «уровень безра- ботицы» с использованием второго правила построения отображения шкал. Листовому критерию «уровень расходов на медицину» экспертом был поставлен в соответствие фактор «объем финансирования здравоохранения» когнитивной карты. Шкала для этого критерия построена по правилу 3.
Определение интегрированной модели поддержки принятия решений
Интегрированную модель поддержки принятия решений в неструктурированных ситуациях можно представить следующим кортежем: áCo, Ir, Ф, Y, P, F(XКФ(m), vi)ñ, где Co – когнитивная модель ситуации; Ir – иерархическая модель оценивания; Ф – множество факторов когнитивной модели, Ф Ì F, подобных по смыслу листовым критериям иерар- хической модели оценивания K, Ф = {fi Î F, lj Î K: fi ~ lj, j = 1, n}, ~ – смысловое подобие факторов из множеств F и K; Y = {yi} – множество отображений шкал факторов когнитивной модели X в шкалы листовых критериев модели иерархического оценивания Y, yi : Xi ® Yi; P = {PK} – множество альтернатив интегрированной модели поддержки принятия решений; F(XКФ(m), vi) – оценки достижимости генеральной цели альтернативой интегрированной модели поддержки принятия решений.
Допустим, что эксперт определил некоторое множество возможных управляющих воздействий P = {PK}, где PK = (p1K, …, pmK) – вектор приращений факторов ситуации в начальный момент времени. Для каждого управляющего воздействия PK Î Р может быть получен прогноз развития ситуации в последовательные дискретные моменты времени XК(0), …, XК(Т), где XК(t) = (x1K(t), …, xmK(t)) – вектор значений всех факторов когнитивной модели в момент времени t. При этом, естественно, в полученном прогнозе будут изменяться и факторы из множества Ф, непосредственно связанные с листовыми критериями модели иерархического оценивания. Тогда иерархическая модель в последовательные моменты времени будет оценивать вектор состояний XКФ(0), …, XКФ(Т), то есть будет получена оценка всех последовательных прогнозных состояний F(XКФ(t), vi).
Альтернативой в интегрированной модели поддержки принятия решений будем называть управляющее воздействие PK Î Р.
Оценкой достижимости генеральной цели альтернативой PK будем называть оценку прогноза развития ситуации для этой альтернативы F(XКФ(m), vi), где m – число факторов когнитивной модели.
В примере рассмотрим следующие альтернативы.
Альтернатива К1 – «Улучшение инвестиционного климата в РФ» реализуется как уменьшение значений факторов «уровень налогов» и «уровень преступности» на 10 %. Альтернатива представляется в виде вектора приращений P1 = (0, 0, 0, 0, –0,044, 0, –0,034, 0, 0, 0, 0, 0, 0, 0, 0, 0).
Альтернатива К2 – «Увеличение социальных трат государства» реализуется как увеличение значения фактора «социальные траты» на 10 %. Вектор, определяющий эту альтернативу, следующий: P2 = (0, 0,07, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0).
Альтернатива К3 – «Усиление борьбы с преступностью» реализуется как уменьшение значений факторов «уровень преступности» на 10 %. Вектор P3 = = (0, 0, 0, 0, 0. 0, –0.034, 0, 0, 0, 0, 0, 0, 0, 0, 0).
Начальное состояние ситуации X(0), прогнозы развития ситуации для каждой альтернативы X1(m), X2(m), X3(m), веса листовых критериев vi и произведения X1Ф(m)×vi, X2Ф(m)×vi, X3Ф(m)×vi представлены в таблице.
Параметры когнитивной карты
Cognitive map parameters
|
№
|
X(0)
|
X1(m)
|
X2(m)
|
X3(m)
|
vi
|
X1Ф(m)vi
|
X2Ф(m)vi
|
X3Ф(m)vi
|
|
1
|
0,26
|
0,264
|
0,281
|
0,26
|
0
|
0
|
0
|
0
|
|
2
|
0,34
|
0,353
|
0,41
|
0,34
|
0
|
0
|
0
|
0
|
|
3
|
0,48
|
0,51
|
0,48
|
0,48
|
0
|
0
|
0
|
0
|
|
4
|
0,47
|
0,4727
|
0,47
|
0,47
|
0,06
|
0,028362
|
0,0282
|
0,0282
|
|
5
|
0,33
|
0,27
|
0,33
|
0,33
|
0
|
0
|
0
|
0
|
|
6
|
0,61
|
0,62
|
0,605
|
0,61
|
0
|
0
|
0
|
0
|
|
7
|
0,32
|
0,286
|
0,32
|
0,286
|
0,1
|
0,0286
|
0,032
|
0,0286
|
|
8
|
0,49
|
0,514
|
0,49
|
0,49
|
0,04
|
0,02056
|
0,0196
|
0,0196
|
|
9
|
0,49
|
0,497
|
0,49
|
0,49
|
0
|
0
|
0
|
0
|
|
10
|
0,31
|
0,325
|
0,31
|
0,31
|
0
|
0
|
0
|
0
|
|
11
|
0,35
|
0,374
|
0,35
|
0,35
|
0
|
0
|
0
|
0
|
|
12
|
0,33
|
0,31
|
0,33
|
0,33
|
0,1
|
0,031
|
0,033
|
0,033
|
|
13
|
0,49
|
0,518
|
0,49
|
0,49
|
0
|
0
|
0
|
0
|
|
14
|
0,56
|
0,569
|
0,56
|
0,56
|
0
|
0
|
0
|
0
|
|
15
|
0,47
|
0,464
|
0,483
|
0,47
|
0,3
|
0,1392
|
0,1449
|
0,141
|
|
16
|
0,48
|
0,492
|
0,48
|
0,48
|
0,4
|
0,1968
|
0,192
|
0,192
|
Оценки достижимости цели для каждой альтернативы, полученные с помощью интегрированной модели, будут следующие:
К1: «Улучшение инвестиционного климата в РФ» –  ;
;
К2: «Увеличение социальных трат государст- ва» –  ;
;
К3: «Усиление борьбы с преступностью» – 
Сравнив оценки достижимости генеральной цели альтернативами К1, К2, К3, полученные в результате работы гибридной модели [7], которая представлена на рисунке 5, и оценки, полученные в классической модели иерархии, видим, что наилучшей альтернативой в обоих случаях является К2, далее идут альтернативы К1 и К3. Однако в интегрированной модели есть возможность генерации альтернатив в зависимости от изменений текущей ситуации.
Модулярная гибридная система прогнозирования временных рядов
Разработанная система прогнозирования базируется на модулярной архитектуре, придающей системе дополнительную устойчивость: даже если один из модулей выходит из строя, остальные модули продолжают выполнять свою работу [8].

 Сама система имеет три основных модуля, отвечающих за задачу прогнозирования. Гибридная нейро-нечеткая сеть выполняет прогноз временного ряда на основе численных показателей и дает так называемый количественный прогноз, результаты которого проходят через систему верификации (оценки адекватности прогноза); если прогноз соответствует необходимой точности, он передается на следующий модуль. Параллельно с нейро-нечеткой сетью работает модуль с НКК, который получает на вход данные о событийном влиянии на временной ряд, строится когнитивная карта, в которой учитываются все факторы влияния на конкретный прогнозируемый показатель. На выходе когнитивная карта дает прогноз с вероятностью его выполнения, то есть с консонансом фактора, который говорит, выполнится прогноз или нет. Далее все данные, полученные с этих модулей, поступают на третий модуль, работающий на основе нейронной сети, который агрегирует информацию, полученную с предыдущих модулей, и выдает итоговый прогноз. На рисунке 6 изображена схема системы прогнозирования.
Сама система имеет три основных модуля, отвечающих за задачу прогнозирования. Гибридная нейро-нечеткая сеть выполняет прогноз временного ряда на основе численных показателей и дает так называемый количественный прогноз, результаты которого проходят через систему верификации (оценки адекватности прогноза); если прогноз соответствует необходимой точности, он передается на следующий модуль. Параллельно с нейро-нечеткой сетью работает модуль с НКК, который получает на вход данные о событийном влиянии на временной ряд, строится когнитивная карта, в которой учитываются все факторы влияния на конкретный прогнозируемый показатель. На выходе когнитивная карта дает прогноз с вероятностью его выполнения, то есть с консонансом фактора, который говорит, выполнится прогноз или нет. Далее все данные, полученные с этих модулей, поступают на третий модуль, работающий на основе нейронной сети, который агрегирует информацию, полученную с предыдущих модулей, и выдает итоговый прогноз. На рисунке 6 изображена схема системы прогнозирования.
Далее более подробно рассмотрим модуль, являющийся гибридом НКК и нейро-нечеткой сети ANFIS.
Гибридный подход к прогнозированию на основе НКК и нейронных сетей
Данный подход позволяет повысить точность прогнозирования благодаря использованию в качестве входных данных нейронной сети узлы НКК. Не секрет, что большое влияние на точность прогноза оказывает выборка данных, на которой строится прогноз.
Подход имеет две основные стадии [9]. На первой стадии разрабатывается модель НКК по историческим данным временных рядов с помощью генетического алгоритма обучения [10].
Этапы первой стадии:
- инициализация НКК по историческим данным временных рядов;
- построение оптимизированной НКК (выбирая наиболее значимые концепты и их соединения) с помощью генетического алгоритма [8];
- тестирование НКК на основе нормализованных проверочных данных.
Используем концепты НКК для определения входов для нейронной сети для повышения точности прогнозирования. Вторая стадия состоит из следующих шагов:
- повышение точности прогнозирования, используя отобранные входные данные – концепты разработанной когнитивной карты;
- обучение нейронной сети;
- тестирование полученной нейронной сети на тестовых данных.
 Подобный пример, изображенный на рисунке 7, представляет процесс прогнозирования такого показателя, как «качество жизни населения». Использование когнитивной карты в данной ситуации наиболее целесообразно по следующей причине: чтобы построить качественный прогноз данного показателя, как многих других, необходимо выделить наиболее влияющие на него факторы. Когнитивная карта наилучшим образом помогает решить подобную задачу и тем самым подать на входы нейронной сети подготовленные данные концептов когнитивной карты.
Подобный пример, изображенный на рисунке 7, представляет процесс прогнозирования такого показателя, как «качество жизни населения». Использование когнитивной карты в данной ситуации наиболее целесообразно по следующей причине: чтобы построить качественный прогноз данного показателя, как многих других, необходимо выделить наиболее влияющие на него факторы. Когнитивная карта наилучшим образом помогает решить подобную задачу и тем самым подать на входы нейронной сети подготовленные данные концептов когнитивной карты.
Заключение
Результаты данной работы показывают эффективность создания гибридных систем как для задачи принятия решений, так и для задачи прогнозирования временных рядов. Представлена интегрированная гибридная модель поддержки принятия решений, объединяющая метод анализа иерархий Саати и НКК. Подобное решение послужило фундаментом для разработки системы прогнози- рования временных рядов. Представлена новая модель модулярной системы прогнозирования временных рядов. Подробно рассмотрен один из модулей данной системы, содержащий в себе гибридную подсистему, состоящую из комбинации НКК и нейро-нечеткой сети ANFIS.
Работа выполнена при частичной поддержке РФФИ, гранты №№ 17-07-01558 и 17-37-50013.
Литература
1. Kosko B. Fuzzy cognitive maps. Intern. Jour. of Man-Machine Studies, 1986, vol. 24, pp. 65–75.
2. Канеман Д., Словик П., Тверски А. Принятие решений в неопределенности: правила и предубеждения; [пер. с англ.]. Харьков: 2005. 632 с.
3. Аверкин А.Н., Кузнецов О.П., Кулинич А.А., Титова Н.В. Поддержка принятия решений в слабоструктурированных предметных областях: анализ ситуации и оценка альтернатив // Изв. РАН: Теория и системы управления. 2005. С. 139–149.
4. Абдикеев Н.М., Аверкин А.Н., Ефремова Н.А. Когнитивная экономика в эпоху инноваций // Вестн. РЭА. 2010. № 1. С. 3–20.
5. Ключарев В.А., Шестакова А.Н. Нейроэкономика: нейробиология принятия решений // Экспериментальная психология. 2011. Т. 4. № 2. С. 14–35.
6. Кулинич А.А. Методология когнитивного моделирования сложных плохо определенных ситуаций // Вторая Междунар. конф. по проблемам управления: тр. конф. М.: Изд-во ИПУ РАН, 2003.
7. Кулинич А.А., Титова Н.В. Модель оценки альтернатив управления слабоструктурированными динамическими ситуациями // Десятая Национальн. конф. по искусствен. интеллекту с междунар. участ. КИИ-2006: тр. конф. М.: Физматлит, 2006.
8. Ярушев С.А., Аверкин А.Н. Модулярная система прогнозирования на основе нечетких когнитивных карт и нейро-нечетких сетей // Нечеткие системы, мягкие вычисления и интеллектуальные технологии (НСМВИТ-2017): тр. VII Всерос. науч.-практич. конф. СПб: Политехника-сервис, 2017. С. 189.
9. Papageorgiou E.I., Poczęta K. A two-stage model for time series prediction based on fuzzy cognitive maps and neural networks. Neurocomputing, 2017, vol. 232, pp. 113–121.
10. Papageorgiou E. I. Learning algorithms for fuzzy cognitive maps – a review study. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2012, vol. 42, no. 2, pp. 150–163.
References
- Kosko B. Fuzzy Cognitive Maps. Int. Jour. of Man-Machine Studies. 1986, vol. 24, pp. 65–75.
- Kahneman D., Slovik P., Tversky A. Decision Making in Uncertainty: Rules and Prejudices. Kharkiv, 2005, 632 p.
- Averkin A.N., Kuznetsov O.P., Kulinich A.A., Titova N.V. Decision-making support in weakly structured subject domains: analysis of situations and evaluation of alternatives. Izvestya RAN. Teoriya i systemy upravleniya [Journal of Computer and Systems Sciences International]. 2006, iss. 3, pp. 469–479.
- Abdikeev N.M., Averkin A.N., Efremova N.A. Cognitive economics in the era of innovation. Vestnik REA [RUE Bulletin]. 2010, no. 1, pp. 3–20 (in Russ.).
- Klyucharev V.A., Shestakova A.N. Neuroeconomics: neurobiology of decision-making. Eksperimentalnaya psikhologiya [Experimental Psychology]. 2011, vol. 4, no. 2, pp. 14–35 (in Russ.).
- Kulinich A.A. Methodology of cognitive modeling of complex ill-defined situations. 2-ya Mezhdunar. konf. po problemam upravleniya: tr. konf. [Proc. 2nd Int.l Conf. on Management Problems]. Moscow, IPU RAN Publ., 2003.
- Kulinich A.A., Titova N.V. The alternatives evaluation model for managing weakly structured dynamic situations.
10-ya Nats. konf. po iskusstven. intellektu s mezhdunar. uchast. KII-2006: tr. konf. [Proc. 10th National Conf. on Artificial Intelligence with Int. Participation KII-2006]. 2006, Moscow, Fizmatlit Publ., 2006 (in Russ.).
- Yarushev S.A., Averkin A.N. Modular forecasting system based on fuzzy cognitive maps and neural-fuzzy networks. Nechetkie sistemy, myagkie vychisleniya i intellektualnye tekhnologii (NSMVIT-2017): tr. VII Vseros. nauch.-praktich. konf. [Proc. 7th All-Russian Scientific and Practical Conf. “Fuzzy systems, Soft Computing and Intelligent Technology” (NSMVIT-2017)]. St. Petersburg, Politekhnika-servis Publ., 2017, vol. 1, pp. 189 (in Russ.).
- Papageorgiou E.I., Poczęta K. A two-stage model for time series prediction based on fuzzy cognitive maps and neural networks. Neurocomputing. 2017, vol. 232, pp. 113–121.
- Papageorgiou E.I. Learning algorithms for fuzzy cognitive maps – a review study. IEEE Trans. on Systems, Man, and Cybernetics. Part C (Applications and Reviews). 2012, vol. 42, no. 2, pp. 150–163.





 , где {xij} – множество значений фактора fi когнитивной модели, заданных на отрезке числовой оси на [0, 1];
, где {xij} – множество значений фактора fi когнитивной модели, заданных на отрезке числовой оси на [0, 1];  – множество значений соответствующего листового критерия lm иерархии,
– множество значений соответствующего листового критерия lm иерархии,  Î [0, 1].
Î [0, 1]. для следующих трех случаев.
для следующих трех случаев. – тождественная функция, значит, каждое значение шкалы фактора равно значению шкалы критерия, то есть
– тождественная функция, значит, каждое значение шкалы фактора равно значению шкалы критерия, то есть 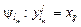 , где j – количество градаций шкалы фактора fi.
, где j – количество градаций шкалы фактора fi.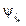 имеет следующий вид:
имеет следующий вид:  , i = 1, j, где j – количество градаций шкалы фактора fi.
, i = 1, j, где j – количество градаций шкалы фактора fi. не может быть определено перечисленными выше способами. В этом случае предлагается построить шкалу критерия lm и каждому значению xij шкалы фактора fi поставить в соответствие значение на шкале критерия lm, то есть
не может быть определено перечисленными выше способами. В этом случае предлагается построить шкалу критерия lm и каждому значению xij шкалы фактора fi поставить в соответствие значение на шкале критерия lm, то есть  .
. ;
; ;
;


