Метод определения возможностей параллельного выполнения функций алгоритмов анализа данных
| Холод И.И. (iiholod@mail.ru) - Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) (доцент), Санкт-Петербург, Россия, кандидат технических наук | |
| Ключевые слова: параллельные алгоритмы, распределенные системы, data mining, зависимость по данным |
|
| Keywords: parallel algorithms, distributed systems, data mining, data dependency |
|
|
|
|
Широкое внедрение информационных технологий приводит к появлению больших объемов хранящейся информации. Такая информация может размещаться на множестве распределенных узлов и в хранилищах (хранилищах данных [1], «облаках» [2] и т.п.), объединенных единой сетью. В связи с этим возрастает потребность в параллельной и распределенной обработке данных. Одним из видов обработки данных является анализ. Алгоритмы анализа данных характеризуются следующими особенностями: - неизменяемость анализируемых данных; - создание моделей знаний малого объема при анализе больших объемов входных данных; - извлечение из данных закономерностей сложными функциями, обрабатывающими несколько произвольных объектов из набора данных (не обладающими свойством списочного гомоморфизма); - наличие ярко выраженной итерационной структуры с множеством циклов, обрабатывающих данные и элементы строящейся модели знаний. Для параллельного и распределенного выполнения таких алгоритмов необходимы методы распараллеливания для систем как с распределенной, так и с общей памятью. Такие методы должны учитывать зависимости по данным между распа- раллеливаемыми функциями. В настоящее время известны условия Бернштейна для параллельного выполнения отдельных операций программ. Они являются достаточными, но не необходимыми. В данной статье описывается метод определения возможности параллельного выполнения функций алгоритма анализа данных в системах с общей памятью и в распределенных системах. Представление алгоритма анализа в виде композиции функций Для определения возможностей параллельного выполнения алгоритм анализа данных должен быть представлен в виде композиции функций [3]: dma = fn ° fn–1 °…° fi ° …° f1° f0, (1) где функция f0 : D → M принимает в качестве аргумента набор данных d Î D (D – множество наборов данных) и возвращает созданную по нему модель знаний m0 Î M (M – множество моделей знаний); функции fi : M → M, i = 1, ..., n, принимают в качестве входного аргумента модель знаний mi–1 Î M, построенную предыдущей функцией fi–1, и возвращают измененную модель знаний mi Î M. Набор данных содержит характеристики объектов (людей, элементов и др.), описываемых атрибутами (возраст, пол, вес и др.), и его часто представляют в виде 2-мерной матрицы для z объектов и их p атрибутов [4, 5]: d = (xj.k) где xj.k – значение k-го атрибута для j-го объекта. Набор возможных значений k-го атрибута обозначается как Defk (xj.k Î Defk). Строка матрицы (2) является вектором. Модель знаний m Î M содержит закономерности, извлеченные из набора данных d алгоритмом анализа данных dma. Такие закономерности являются элементами модели знаний (классификационные и ассоциативные правила, центры кластеров, узлы деревьев решений и т.п.). Существуют различные способы формального представления знаний: продукционные модели [6], семантические сети [7], фреймы [8] и др. Модель знаний, получаемая в результате выполнения алгоритмов анализа данных, может быть представлена в виде массива деревьев унифицированных элементов, для которых определены функции, позволяющие выполнять их параллельное построение [9]: m : [E], m = [e1, e2, …, ev, …, ew]. (3) Для индексации элементов модели знаний используем децимальную нотацию индексации элементов леса деревьев. Для хранения и обработки индексов в децимальной нотации – список целых чисел. Первое число индекса обозначает корневой элемент соответствующего дерева в модели знаний m[v] ≡ ev, следующие числа в индексе – позиции элементов модели знаний среди узлов-потомков дерева. Например, элемент модели знаний m[2, 1, 3] обозначает 3-й элемент модели знаний среди узлов-потомков 1-го узла среди узлов-потомков корневого узла 2-го дерева модели знаний m. Все множество индексов модели знаний обозначим символом I. Каждый элемент модели знаний описывает некоторую закономерность с помощью набора параметров и содержит множество дочерних элементов: e : E = <[P], [E]>, e = <[p1, p2, …, pd, …, pf], [e1, e2, …, ev, …, ew]>. При этом элементы модели знаний, являющиеся дочерними элементами одного и того же элемента, должны иметь одинаковый набор параметров. Для представления цикла алгоритма анализа введена функция высшего порядка, описывающая итерационную обработку данных строящейся модели знаний в виде композиции функции, применяемой к разным элементам модели знаний: loope : I ® I ® (M ® M) ® M ® M loope is ie ft m = (ft m[ie]) °…° (ft m[is]), где ie и is – индексы первого и последнего элементов модели знаний, обрабатываемых в цикле. Цикл, выполняющий итерационную обра- ботку элементов набора данных d (2), также может быть представлен в виде композиции функции, применяемой к разным векторам набора данных: loopd : I ® I ® (M ® M) ® D ® M, loopd is ie ft d = loopd (ft d[ie]) °…° (ft d[is]) ft d, где ie и is – индексы первого и последнего векторов набора данных, обрабатываемых в цикле. В процессе выполнения функция анализа данных fi может использовать не все элементы модели знаний mi–1, являющейся ее входным аргументом. Кроме того, результат ее работы может привести к изменению только некоторых элементов итоговой модели знаний mi. Для анализа зависимостей по данным [10, 11] между функциями алгоритма анализа данных используем соответствующие обозначения: - In(fi) – множество элементов входной модели знаний mi–1, используемых функцией fi в процессе выполнения; - Out(fi) – множество элементов выходной модели знаний mi, изменяемых функцией fi в процессе выполнения. Для распараллеливания последовательных алгоритмов и их выполнения в системах с общей и распределенной памятью введена функция высшего порядка parallel [3]: parallel : Boolean ® [(M ® M)] ® M ® M parallel s [f1, …, fk] m = if (s = = true) fork [f1, …, fk] m else join m (fork[f1, …, fk] clone m). Она использует функцию высшего порядка fork, которая принимает список функций и модель знаний, применяет каждую функцию из списка к модели знаний и полученную модель знаний добавляет в возвращаемый список: fork : [M ® M] ® M ® [M] fork [f1, …, fk] m = [(run f1 clone m), …, (run fk clone m)] = [m1, …, mk]. В функции parallel первый булевский аргумент s определяет способ выполнения: с общей или распределенной памятью. Для систем с распределенной памятью, когда каждая параллельно выполняющаяся функция работает с аргументами, хранящимися в отдельной памяти, для создания отдельных копий модели знаний может использоваться функция клонирования clone [9]. Параллельно построенные модели знаний m1, …, mk, также хранящиеся в отдельных областях памяти, должны объединяться в единую модель знаний mr. Для этого может быть использована функция объединения join [9]. При параллельном выполнении в системах с общей памятью необходимо учитывать, что все изменения с моделью знаний, реализуемые параллельными функциями, осуществляются над одним и тем же экземпляром модели знаний, хранящейся в общей памяти. Это означает, что аргументами параллельных функций является один и тот же экземпляр модели знаний, что не требует клонирования модели знаний и ее объединения. За счет этого параллельное выполнение функций алгоритма анализа данных в системах с общей памятью более эффективно. Частичное применение функции parallel с фиксацией первого аргумента позволяет получить функция распараллеливания: - для систем с общей памятью: parallels : [(M ® M)] ® M ® M parallels = parallel true [fr, …, fs] m = fork[f1, …, fk] m; - для систем с распределенной памятью: paralleld : [(M ® M)] ® M ® M paralleld = parallel false [fr, …, fs] m = join m (fork[f1, …, fk] clone m). Необходимые и достаточные условия параллельного выполнения функций алгоритмов анализа данных Согласно условиям Бернстайна [12], достаточные условия для параллельного выполнения функций fi и fi+1 следующие: - отсутствие антизависимости (data anti-dependency): In(fi ) Ç Out(fi+1 ) = Æ; - отсутствие потоковой зависимости (data flow dependency): Out(fi) Ç In(fi+1)= Æ; - отсутствие зависимости по выходу (output dependency): Out(fi) Ç Out(fi+1) = Æ. Данные условия являются достаточными, но не необходимыми для параллельного выполнения функций fi и fi+1. Определим необходимые условия для параллельного выполнения пары функций алгоритма анализа данных для систем как с общей, так и с распределенной памятью. При параллельном выполнении в системах с общей памятью функции fi и fi+1 строят общую модель знаний и существует вероятность, что функция fi+1 будет выполнена до функции fi: fi+1°fi mi–1 = fi°fi+1 mi–1. Следовательно, для корректности параллельного выполнения функций fi и fi+1 с общей моделью знаний они должны быть ассоциативными. Это возможно при следующих условиях: - если функции fi и fi+1 не используют и не изменяют общие элементы модели знаний (то есть выполняются условия Бернстайна); - если функции fi и fi+1 выполняют над общими для них элементами модели знаний только ассоциативные по отношению друг к другу операции oi и oi+1 (то есть операции, которые могут выполняться в любом порядке): oi+1(oi(mi–1[r])) = oi(oi+1(mi–1[r])) для mi–1[r] Î Î (In(fi) Ç Out(fi+1)) È (Out(fi) Ç In(fi+1)) È È (Out(fi) Ç Out(fi+1)). Ассоциативными являются операции, изменяющие свойства элементов модели знаний, например, суммирование, вычитание, инкрементация и т.п. Операции, выполняющие добавление или удаление элементов модели знаний, не являются ассоциативными. При параллельном выполнении в системах с распределенной памятью функции fi и fi+1 независимо строят разные экземпляры модели знаний (mi и mi+1 соответственно), получая на вход модель знаний mi–1, построенную предыдущей функцией. При этом в отличие от последовательного варианта на вход функции fi+1 будет поступать модель знаний mi-1, построенная функцией fi–1, а не функцией fi. Итоговая модель знаний mi+1 должна строиться путем объединения моделей знаний, построенных функциями fi и fi+1 в распределенной памяти функцией join: fi+1°fi mi–1 = join(fi+1 mi–1) (fi mi–1). Таким образом, для корректности параллельного выполнения функций fi и fi+1 с распределенной моделью знаний необходимо, чтобы независимое выполнение функций fi и fi+1 не отличалось от последовательного выполнения, а функция join корректно объединяла модели знаний, построенные независимо. Первое условие будет выполняться, если - элементы модели знаний, используемые функцией fi+1, не изменяются функцией fi, то есть отсутствует потоковая зависимость (Out(fi) Ç Ç In(fi+1) = Æ); - для элементов, входящих в потоковую зависимость, операции oi и oi+1, выполняемые над такими элементами, были ассоциативными: oi+1(oi(mi–1[r])) = oi(oi+1(mi–1[r])) для mi–1[r] Î Î (Out(fi) Ç In(fi+1)); что в том числе позволяет объединять их в функции join после независимого выполнения функций fi и fi+1. Второе условие выполняется, если - функции fi и fi+1 не изменяют общие элементы, то есть отсутствует зависимость по выходу, и в этом случае функция join объединяет множества элементов моделей знаний mi и mi+1; - для операций oi и oi+1, выполняемых над элементами моделей знаний, изменяемых функциями fi и fi+1, существует функция агрегирования Å изменений, сделанных ими независимо в функциях fi и fi+1: oi+1(oi(mi–1[r]) = oi+1(mi–1[r]) Å oi(mi–1[r]) для mi–1[r] Î (Out(fi) Ç Out(fi+1)). Наличие антизависимости между функциями fi и fi+1: In(fi) Ç Out(fi+1) ≠ Æ в системах с распределенной памятью невозможно, так как результаты параллельно выполненных функций физически разделены. Таким образом, оно не является необходимым. Метод проверки условий параллельного выполнения функций алгоритма анализа данных Верификация достаточных и необходимых условий для параллельного выполнения пары функций fi и fi+1 включает: 1) проверку наличия потоковой зависимости FD = Out(fi) Ç In(fi+1) и при ее наличии проверку ассоциативности операций, выполняемых над эле- ментами модели знаний, входящими в нее; 2) проверку наличия антизависимости AD = = In(fi) Ç Out(fi+1) и при ее наличии проверку ассоциативности операций, выполняемых над элементами модели знаний, входящими в нее; 3) проверку наличия зависимости по выходу OD = Out(fi) Ç Out(fi+1) и при ее наличии проверку а) ассоциативности операций, выполняемых над элементами модели знаний, входящими в нее; б) существования операции агрегирования для элементов модели знаний, входящих в нее. Порядок выполнения перечисленных проверок следующий: 1. выполняется проверка 1 и при ее выполнении 2. выполняется проверка 2 2.1. при ее выполнении 2.1.1. выполняется проверка 3a для проверки возможности параллельного выполнения с общей памятью функцией parallels; 3. независимо от результатов проверки 2 выполняется проверка 3б для проверки возможности параллельного выполнения с распределенной памятью функцией paralleld. Представим псевдокод метода. verifyParallelize (fr, fr+1) – функция проверки возможности параллельного выполнения функций алгоритма анализа данных Вход: пара функций fr и fr+1, для которых выполняется распараллеливание Выход: функция parallel, если параллельное выполнение возможно, и null иначе verifyParallelize(fi, fi+1) FD = Out(fi) Ç In(fi+1); // множество элементов модели знаний, составляющих потоковую зависимость AD = In(fi) Ç Out(fi+1); // множество элементов модели знаний, составляющих антизависимость OD = Out(fi) Ç Out(fi+1); // множество элементов модели знаний, составляющих зависимость по выходу if (FD ≠ Æ) // проверка наличия потоковой зависимости for each e from FD // для каждого элемента модели знаний из потоковой зависимости if oi+1(oi(e)) ≠ oi(oi+1(e)) // проверить ассоциативность операций, выполняемых над ним return null; if (AD È OD ≠ Æ) // проверка наличия антизависимости или зависимости по выходу for each e from AD È OD // для каждого элемента из антизависимости или зависимости по выходу if oi+1(oi(e)) ≠ oi(oi+1(e)) // проверить ассоциативность операций, выполняемых над ним return null return parallels; if (OD ≠ Æ) // проверка наличия зависимости по выходу for each e from OD // для каждого элемента модели знаний из зависимости по выходу if return null return paralleld; Если допустимо параллельное выполнение и с общей, и с распределенной памятью, должна использоваться функция parallels как наиболее эф- фективная (не использующая функции клонирова- ния и объединения моделей знаний). Проверка возможности параллельного выполнения функций выполняется в два этапа: - проверка возможности распараллеливания по задачам – выполняется проверка необходимых и достаточных условий для каждой пары функций, находящихся на одном уровне композиции; - проверка возможности распараллеливания по данным – выполняется проверка необходимых и достаточных условий для функций, вызывающихся итерационно в каждом цикле на разных итерациях. Пример распараллеливания алгоритма анализа данных 1R Рассмотрим распараллеливание с помощью описанного метода алгоритма классификации 1R [13]. Он формирует модель знаний m в виде простых правил классификации. Такие правила строятся по значению одного атрибута, поэтому в литературе алгоритм часто называют «1‑правило» (1‑rule). В соответствии с предложенным подходом модель знаний, представленная в виде леса деревьев (3), будет включать в себя следующие четыре дерева [3]: · m[0] – дерево метаданных набора данных d, где m[0, k] – элемент модели знаний, содержащий информацию о k-м атрибуте ak и его значениях. · m[1] – дерево классификационных правил, построенных алгоритмом 1R, в котором: - m[1].n – параметр, определяющий количество входящих в массив векторов, удовлетворяющих правилам (корректных векторов); - m[1, p] – классификационное правило, простейший вид которого может быть определен как набор параметров: m[1, p] = , где ak – атрибут ak Î A, значение которого проверяется правилом; vk.q – значение атрибута ak, с которым сравнивается значение вектора; vt.p – предсказываемое правилом значение зависимого атрибута at, vt.p Î Def(at); n – параметр, определяющий количество корректных векторов – векторов, для которых данное правило является верным: n = = |{xj : xj Î X, (ak(xj) = vk.q и at(xj) = vt.p)}|. · m[2] – дерево простых правил кандидатов. · m[3] – дерево, хранящее информацию о количестве векторов для каждой комбинации: значения независимого атрибута ak, значения зависимого атрибута at: - m[3, k] содержит элементы, соответствующие значениям независимого атрибута ak; - m[3, k, q] содержит элементы, соответствующие значению vk.q независимого атрибута ak; - m[3, k, q].mi – индекс (mi: 1..u) значения зависимого атрибута at (класса), для которого имеется максимальное количество векторов (соответствует переменной mi); - m[3, k, q, p] – количество векторов, имеющих соответствующие значения независимого атрибута ak и зависимого атрибута at: m[3, k, q, p] = = |{xj|ak(xj) = vk.q, at(xj) = vt.p, xj Î X, ak, at Î A, vk.q Î Î Def(ak), vt.p Î Def(at)}|. Представим псевдокод реализации алгоритма 1R в библиотеке Weka. // Для каждого атрибута For k = 0 ... |A| // Для каждого атрибута подсчитать появление каждого класса For j = 1 … |X| m[3, k, d[j, k], d[j, t]]++; For q = 1 … |Defk| // найти наиболее частый класс For p = 1 … |Deft| if m[3, k, m[0, k, q], m[0, t, p]] > m[3, k, m[0, k, q], m[3, k, m[3, k, q]].mi] m[3, k, q].mi = p; // сделать правило для класса и значения атрибута m[2].add( m[3, k, m[0, k, q], m[3, k, m[3, k, q]].mi]}) // вычислить ошибку класса m[2].n+= m[3, k, m[0, k, q], m[3, k, m[0, k, q]].mi] //Выбрать правило с минимальной ошибкой if(m[2].n > m[1].n) m[1].n = m[2].n; m[1] = m[2]; m[2].cleare; Сам алгоритм 1R в виде композиции функций (1) имеет вид [3]: 1R = f1°f0 = (4) = (loope [0, 1] [0, p] f11°f10°f4°f2)°f0 = = (loope [0, 1] [0, p] f11°f10°(loope [0, k, 1] [0, k, u] f9°f8°f5)°(loopd [0] [z] f3))°f0 = = (loope [0, 1] [0, p] f11°f10°(loope [0, k, 1] [0, k, u] f9°f8°(loope [0, t, 1] [0, t, y] f6))°(loopd [0] [z] f3))°f0, где f1 – цикл по метаданным с m[0, 1] по m[0, p]: f1 = loope [0, 1] [0, p] (f13°f10°f4°f2); f2 – цикл по векторам набора данных с d[0] по d[z]: f2 = loopd [0] [z] f3; f3 – функция, выполняющая инкрементацию количества корректных векторов m[3, k, q, p] для зна- чений vk.q независимого атрибута ak и значений vt.p зависимого атрибута at; f4 – цикл по значениям независимого атрибута ak с m[0, k, 1] по m[0, k, u]: f4 = loope [0, k, 1] [0, k, u] (f9°f8°f5); f5 – цикл по значениям зависимого атрибута at с m[0, t, 1] по m[0, t, y]: f5 = loope [0, t, 1] [0, t, y] f6; f6 – функция, выполняющая поиск элемента модели знаний с максимальным значением количества корректных векторов m[3, k, q, p] среди элементов поддерева m[3, k, q] и запоминающая его индекс в поле m[3, k, q].mi; f8 – функция, выполняющая добавление правила m[2, p] с максимальным количеством корректных векторов во множество правил кандидатов m[2]; f9 – функция, выполняющая подсчет корректных векторов m[2, p].n для одного атрибута ak; f10 – функция, выполняющая выбор лучшего набора правил (m[1] или m[2]) для одного атрибута; f11 – функция, выполняющая удаление набора правил кандидатов из m[2] для одного атрибута. Множества используемых и изменяемых элементов функций алгоритма 1R, определенные на основании псевдокода, представлены в таблице. Для алгоритма 1R возможности распараллеливания по задачам для каждого уровня композиции будут следующими: · функции f0 и f1 не могут выполняться параллельно, так как имеют потоковую зависимость по элементу модели знаний m[0]: Out(f0) Ç In(f1) = = {m[0]} ≠ Æ, над которым в них выполняются не ассоциативные по отношению друг другу операции добавления и извлечения; · функции f2 и f4 не могут выполняться параллельно, так как имеют потоковую зависимость по элементу модели знаний m[3, k]: Out(f2) Ç In(f4) = = {m[3, k]} ≠ Æ, над которым в них выполняются не ассоциативные по отношению друг другу операции инкрементации и сравнения; · функции f4 и f10 не могут выполняться параллельно, так как имеют потоковую зависимость по элементу модели знаний m[2]: Out(f4) Ç In(f10) = = {m[2]} ≠ Æ, над которым в них выполняются не ассоциативные по отношению друг другу операции добавления и извлечения; · функции f10 и f11 могут выполняться параллельно только с распределенной памятью, так как - не имеют потоковой зависимости Out(f10) Ç Ç In(f11) = Æ и зависимости по выходу Out(f10) Ç Ç Out(f11) ≠ Æ; - имеют антизависимость по элементу модели знаний m[2]: In(f10) Ç Out(f11) = {m[2]}, над которым в них выполняются не ассоциативные по отношению друг другу операции удаления и извлечения; · функции f5 и f8 не могут выполняться параллельно, так как имеют потоковую зависимость по элементу модели знаний m[3, k, q’].mi: Out(f5) Ç Ç In(f8) = {m[3, k, q’].mi} ≠ Æ, над которым в них выполняются не ассоциативные по отношению друг другу операции поиска (присваивания индекса максимального элемента) и чтения; · функции f8 и f9 могут выполняться параллельно, так как - не имеют потоковой зависимости: Out(f8) Ç Ç In(f9) = Æ; - не имеют антизависимости: In(f8) Ç Out(f9) = Æ; - не имеют зависимости по выходу: Out(f8) Ç Ç Out(f9) = Æ. Возможности распараллеливания по данным для каждого цикла будут следующими: · композиция функций f11°f10°f4°f2 для разных итераций k и k + 1 не может быть распараллелена по данным, так как имеется потоковая зависимость по элементам модели знаний m[1] и m[2]: Out (f11°f10°f4°f2 для k) Ç In (f11°f10°f4°f2 для k + 1) = = {m[1], m[2], m[3, k]} Ç {d, m[0, k + 1], m[1], m[2], m[3, k + 1]} = {m[1], m[2]} ≠ Æ, над которыми в ней выполняются не ассоциативные по отношению друг другу операции добавления, удаления и извлечения; · композиция функций f9°f8°f5 для разных итераций q и q + 1 может быть распараллелена по данным, так как - существуют потоковая зависимость и ан- тизависимость по элементу m[2].n: Out (f9°f8°f5 для q) Ç In (f9°f8°f5 для q + 1) = {m[3, k, q’].mi, m[2], m[2].n} Ç {m[0, k, q + 1], m[0, t], m[3, k, q + 1], m[2].n} = {m[2].n} ≠ Æ; - In (f9°f8°f5 для q) Ç Out (f9°f8°f5 для q + 1) = = {m[0, k, q], m[0, t], m[3, k, q], m[2].n} Ç {m[3, k, q’].mi, m[2], m[2].n} = {m[2].n} ≠ Æ, над которым выполняется ассоциативная операция инкрементации; - имеется зависимость по выходу по эле- ментам модели знаний m[2] и m[2].n: Out (f9°f8°f5 для q) Ç Out (f9°f8°f5 для q + 1) = {m[3, k, q’].mi, m[2], m[2].n } Ç {m[3, k, q’].mi, m[2], m[2].n} = {m[2], m[2].n } ≠ Æ, над которым выполняется ассоциативная операция инкрементации и для которого существует операция агрегирования – суммирование; · функция f6 для разных итераций p и p + 1 не может быть распараллелена по данным, так как - нет потоковой зависимости: Out (f6 для p) Ç Ç In (f6 для p + 1) = {m[3, k, q’].mi} Ç {m[0, k, q], m[0, t, p + 1], m[3, k, q’, p’], m[3, k, q’, p”]} = Æ; - нет антизависимости: In(f6 для p) Ç Out(f6 для p + 1) = {m[0, k, q], m[0, t, p], m[3, k, q’, p’], m[3, k, q’, p”]} Ç {m[3, k, q’].mi} = Æ; - но имеется зависимость по выходу по элементу m[3, k, q’].mi: Out(f6 для p) Ç Out(f6 для p + 1) = {m[3, k, q’].mi} Ç {m[3, k, q’].mi} ≠ Æ, над которым выполняется неассоциативная операция поиска (присваивания индекса максимального элемента), а также отсутствует функция агрегирования; · функция f3 для разных итераций j и j+1 может быть распараллелена по данным, так как - нет потоковой зависимости: Out (f3 для j) Ç Ç In (f3 для j + 1) = {m[3, k, q, p]} Ç {d[j + 1, k], d[j + 1, t]} = Æ; - нет антизависимости: In (f3 для j) Ç Out (f3 для j + 1) = {d[j, k], d[j, t]} Ç {m[3, k, q, p]} = Æ; - имеется зависимость по выходу по элементу модели знаний m[3, k, q, p]: Out (f3 для j) Ç Ç Out (f3 для j + 1) = {m[3, k, q, p]} Ç {m[3, k, q, p]} = {m[3, k, q, p]} ≠ Æ, над которым выполняется ассоциативная операция инкрементации и для которого существует операция агрегирования – суммирование. Таким образом, распараллеливание алгоритма 1R, представленного выражением (4), может быть выполнено следующим образом: 1RPar = (loope [0, 1] [0, p] paralleld [f10, f11]° (paralleld [loope [0, k, 1] [0, k, u] (parallels [f8 f9]) ° (loope [0, t, 1] [0, t, y] f6)]) °(parallels [loopd [0] [z] f3)])°f0. Программная реализация и эксперименты, подтверждающие эффективность такого распараллеливания, описаны в статье [3]. Заключение В данной работе рассмотрены достаточные и необходимые условия параллельного выполнения функций алгоритмов анализа данных, учитывающие множества используемых и изменяемых элементов моделей знаний. Для систем с общей памятью достаточными и необходимыми условиями являются: - наличие свойства ассоциативности у операций, выполняемых над элементами модели знаний, входящих в потоковую зависимость, или отсутствие таких элементов; - наличие свойства ассоциативности у операций, выполняемых над элементами модели знаний, входящих в антизависимость, или отсутствие таких элементов; - наличие свойства ассоциативности у операций, выполняемых над элементами модели знаний, входящих в зависимость по выходу, или отсутствие таких элементов. Для систем с распределенной памятью достаточными и необходимыми условиями являются: - наличие свойства ассоциативности у операций, выполняемых над элементами модели знаний, входящих в потоковую зависимость, или отсутствие таких элементов; - существование операции агрегирования для элементов модели знаний, входящих в зависимость по выходу, или отсутствие таких элементов. Для выполнения проверки возможностей параллельного выполнения функций алгоритмов анализа данных предложен метод, который осуществляет проверки в заданном порядке и определяет наиболее эффективную функцию для распараллеливания как по задачам, так и по данным для систем с общей и распределенной памятью. Литература 1. Inmon W.H. Building the data warehouse. Wiley Publ., 2005, 523 p. 2. Antonopoulos N., Gillam Lee. Cloud computing: principles, systems and applications. Springer, 2010, 379 p. 3. Kholod I., Shorov A., and Gorlatch S. A Functional Approach to Parallelizing Data Mining Algorithms in Java. Springer, LNCS, 2017, vol. 10421, pp. 459–472. DOI: 10.1007/978-3-319-62932-2_44. 4. Hastie T., Tibshirani R., Friedman J. The elements of statistical learning: data mining, inference and prediction, Springer, NY, 2001, 533 p. 5. Han J., Kamber M. Data mining: concepts and techniques. SF, Morgan Kaufman Publ., 2001, 550 p. 6. Roberts D. The Existential Graphs of Charles S. Peirce. France, The Hague Mouton Publ., 1973, 168 p. 7. Lehmann F., Rodin E.Y. (eds.) Semantic networks in artificial intelligence. NY, Pergamon Press, 1992, vol. 24, 758 p. 8. Минский М. Фреймы для представления знаний; [пер. с англ.]. М.: Энергия, 1979. 151 c. 9. Kholod I.I., Shorov A.V. Unification of mining model for parallel processing. Proc. EIConRus, 2017, pp. 450–455. 10. Banerjee U. Data dependence in ordinary programs. Urbana, 1976, Technical Report, no. 76-837. 11. Banerjee U. An introduction to a formal theory of dependence analysis. The J. of Supercomputing. 1988, vol. 2, pp. 133–149. 12. Bernstein A.J. Program Analysis for Parallel Processing. IEEE Trans. on Electronic Computers, 1966, vol. 15, no. 5, pp. 757–762. 13. Holte R.C. Very simple classification rules perform well on most commonly used datasets. Machine Learning, 1993, vol. 11, pp. 63–90. |
http://swsys.ru/index.php?id=4455&lang=%E2%8C%A9%3Den&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Построение ассоциативных правил в задаче медицинской диагностики
- Математическое моделирование распределенных систем защиты информации
- Программирование, ориентированное на мониторинг, в контексте контролируемого выполнения
- Математическая модель контролируемого выполнения
- Метод частотно-морфологической классификации текстов

 , (2)
, (2)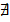 Å // проверить наличие функции агрегирования
Å // проверить наличие функции агрегирования