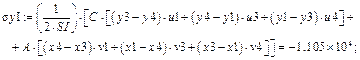Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Расчет конструкций методом конечных элементов в среде математического пакета MathCAD
Аннотация:Рассматриваются возможности математического пакета MathCAD при решении задач прочностного и деформационного расчета строительных и машиностроительных конструкций методом конечных элементов. Показано, что для решения данных задач возможностей математического пакета MathCAD явно недостаточно, так как необходимо обрабатывать достаточно большие объемы информации. Для задач иллюстративного или учебного характера, когда матрица жесткости имеет небольшую размерность и ее компоненты можно ввести в ручном режиме, возможностей пакета MathCAD вполне достаточно, и с его помощью можно получить решение задачи. При этом матрицу жесткости следует формировать путем ручного ввода значений ее компонент, вычисленных заранее в системе MathCAD. В реальных расчетных задачах матрица жесткости имеет большой порядок (порядка тысяч, десятков и сотен тысяч), поэтому для их решения следует использовать специализированные программные комплексы, например ЛИРА, SCAD, ANSYS и другие. В статье рассмотрен конкретный числовой пример расчета пластинки сложного очертания, находящейся в условиях плоского напряженного состояния, методом конечных элементов. Пластинка разбивается на три конечных элемента. Матрица жесткости при этом имеет порядок, равный десяти, и решение задачи получено лишь при ручном вводе значений ее компонент. Полученные результаты можно применять при решении задач расчета строительных и машиностроительных конструкций методом конечных элементов с использованием программно-математического обеспечения персональных компьютеров, в частности, MathCAD.
Abstract:The paper analyses mathematical package MathCAD potential when solving the problems of strength and deformation calculation of building and machine-building constructions using the finite element method. It is shown that MathCAD potentials are definitely not sufficient to solve such problems. It is due to the necessity to process quite a large amount of information. For illustrative and study tasks, when a rigidity matrix has not big dimension and its components can be introduced manually, it is enough to use MathCAD. It can help to solve a problem. In this case, the rigidity matrix should be formed by manual introduction of its component data that were calculated beforehand in MathCAD. In real calculation tasks, a rigidity matrix has a large order (thousands, tens and hundreds of thousands). Therefore, there are specialized software packages to solve them, such as LIRA, SCAD, ANSYS, etc. The paper considers a specific numerical example of calculating a compound profile plate under plain stress condition using the finite element method. The plate is separated into three finite elements. In this case, a rigidity matrix has the order equal to ten; the problem is solved only with manual introduction of its component data.
| Авторы: Бакушев С.В. (bakuchsv@mail.ru) - Пензенский государственный университет архитектуры и строительства (профессор), Пенза, Россия, доктор технических наук | |
| Ключевые слова: метод конечных элементов, матрица жесткости, математический пакет mathcad, персональные компьютеры |
|
| Keywords: finite element method, rigidity matrix, mathematical model mathcad, personal computers |
|
| Количество просмотров: 10294 |
Статья в формате PDF Выпуск в формате PDF (19.46Мб) |
Математический пакет MathCAD, входящий в прикладное программно-математическое обеспечение современных персональных компьютеров, является одним из наиболее популярных средств, предназначенных для решения как чисто математических, так и инженерных задач. Достоинства пакета MathCAD общеизвестны и описаны во многих печатных изданиях, в частности в [1–3]. Простота, доступность, интуитивность пользовательского интерфейса MathCAD приводят к соблазну использовать его для решения достаточно сложных инженерных задач. Действительно, в работах [4–6] и многих других решение математических и инженерных задач реализовано на базе этого математического пакета. Вместе с тем необходимо отметить, что реализация численных методов решения задач, в частности, задач механики деформируемого твердого тела, в системе MathCAD связана с определенными трудностями. Это обусловлено необходимостью обработки достаточно больших объемов информации, с которыми MathCAD зачастую не справляется. К такого типа задачам относятся и задачи расчета строительных и машиностроительных конструкций методом конечных элементов. Это численный метод решения краевых задач для дифференциальных уравнений, в основе которого лежит разбиение области решения на конечные элементы произвольных размеров, но, как правило, одной формы [7–9]. Искомая функция (например, функция перемещений или напряже- ний) внутри конечного элемента аппроксимиру- ется, как правило, полиномом, коэффициенты которого выражаются через значения искомой функции в вершинах конечных элементов. В итоге решение задачи сводится к решению системы линейных алгебраических уравнений относительно значений искомой функции в узлах – вершинах совокупности конечных элементов, покрывающих расчетную область. При этом матрица жесткости, симметричная относительно главной диагонали, имеет, как правило, высокий порядок, хотя и является разреженной. Компоненты матрицы жесткости вычисляются исходя из геометрии рассматриваемой области, способа ее деления на отдельные конечные элементы, а также механических характеристик материала рассчитываемой конструкции. При вычислении перемещений в вершинах конечных элементов матрицу жесткости необходимо обратить. И вот здесь возникают проблемы. Рассмотрим плоское упругое тело, модуль упругости которого E = 2,1×1011 Па, коэффициент Пуассона m = 0,3. Тело находится в условиях обобщенного плоского напряженного состояния. Разделим тело на три треугольных конечных элемента. Проиллюстрируем это рисунком 1, на котором арабскими цифрами обозначены номера вершин конечных элементов, римскими – номера конечных элементов, дугой со стрелкой – направление обхода вершин конечных элементов внутри каждого конечного элемента. К вершинам совокупности конечных элементов приложены составляющие внешних сил Фxi, Фyi. Координаты вершин конечных элементов и величины внешних сил, приложенных к вершинам конечных элементов:
Условия равновесия упругого тела выполняются:
Тело находится в условиях обобщенного плоского напряженного состояния, поэтому
Используя пакет MathCAD, вычисляем компоненты матриц жесткости конечных элементов: КЭ – I: i ® 1, j ® 3, k ® 4.
…
КЭ – II: i ® 1, j ® 4, k ® 2.
…
КЭ – III: i ® 2, j ® 4, k ® 5.
…
Вычисляем компоненты матрицы жесткости K совокупности конечных элементов (в нашем случае матрица жесткости будет десятого порядка). Расчетные формулы будут следующими:
Формируем матрицу жесткости K:
В числах матрица K имеет вид, представленный в таблице 1. Для проверки правильности вычисления значений компонент матрицы жесткости K вычисляем матрицу K–1 и перемножаем матрицу K на матрицу K–1; в результате должны получить единичную матрицу E, представленную в таблице 2. Очевидно, что единичная матрица не получается. Для получения правильного решения введем значения компонент в матрицу K в ручном режиме, сохранив три значащие цифры после запятой (см. рис. 2). Вновь попытаемся вычислить единичную матрицу:
В этом случае результат положительный. Значит, матрица жесткости, сформированная в ручном режиме, является верной. Подтверждение этому – вычисление напряжений в конечных элементах I, II и III. Так как рассчитываемая конструкция (рис. 1) симметрична относительно вертикали, проходящей через вершину 4, и по геометрии, и по внешним силовым воздействиям, напряжения в конечных элементах I и III должны быть одинаковыми (касательные напряжения должны иметь разные знаки). Расчеты показывают, что этому условию удовлетворяет лишь решение, построенное на основе матрицы жесткости K, сформированной путем ручного ввода значений ее компонент: Определяем напряжения. КЭ – I
КЭ – II
КЭ – III
Здесь SI, SII, SIII – площади конечных элементов (м2); sx, sy, txy - напряжения (Па), относящиеся к конечным элементам I, II и III. Заключение Для решения задач расчета строительных и машиностроительных конструкций методом конечных элементов возможностей математического пакета MathCAD явно недостаточно. Для задач учебного или иллюстративного характера, когда матрица жесткости имеет небольшую размерность и ее компоненты можно ввести в ручном режиме, возможностей пакета MathCAD вполне хватает и с его помощью можно получить решение задачи. В реальных расчетных задачах матрица жесткости имеет большой порядок (порядка тысяч, десятков и сотен тысяч), а потому для их решения следует использовать специализированные программные комплексы, например ЛИРА [10], SCAD [11], ANSYS [12] и другие. Полученные результаты могут найти примене- ние при решении задач расчета строительных и машиностроительных конструкций методом конечных элементов с использованием пакетов прикладных программ программно-математического обеспечения персональных компьютеров, в частности, математического пакета MathCAD. Литература 1. Бакушев С.В. Компьютерные технологии решения задач в архитектурно-строительном вузе // Смешанное и корпоративное обучение (СКО-2007): тр. Всерос. науч.-методич. симпоз. 2007. С. 110–113. 2. Рыков С.В., Кудрявцева И.В., Яворская А.Н., Камоц- кий В.И. Использование пакета MathCAD при подготовке студентов экологических и экономических направлений // Науч. журн. НИУ ИТМО. Сер.: Экономика и экологический менеджмент. 2014. № 2. С. 16–24. 3. Половко А.М., Ганичев И.В. MathCAD для студента. СПб: БХВ-Петербург, 2010. 336 с. 4. Макаров Е.Г. Инженерные расчеты в MathCAD. СПб: Питер, 2005. 448 с. 5. Бакушев С.В. Сопротивление материалов. Выполне- ние расчетно-графических работ и решение задач с исполь- зованием математического пакета MathCAD. М., 2006. 6. Охорзин В.А. Прикладная математика в системе MathCAD. СПб: Лань, 2008. 352 с. 7. Зенкевич О., Чанг И. Метод конечных элементов в теории сооружений и в механике сплошных сред; [пер. с англ. А.П. Троицкого, С.В. Соловьева; под ред. Ю.К. Зарецкого]. М.: Недра, 1974. 240 с. 8. Розин Л.Ф. Метод конечных элементов в применении к упругим системам. М.: Стройиздат, 1977. 128 с. 9. Бате К., Вилсон Е. Численные методы анализа и метод конечных элементов. М.: Стройиздат, 1982. 448 с. 10. LiraLand. URL: http://www.liraland.ru (дата обращения: 16.11.2017). 11. SCAD Office. URL: http://www.scadsoft.com (дата обращения: 16.11.2017). 12. ANSYS Discovery Products. URL: http://www.ansys.com (дата обращения: 16.11.2017). |
| Постоянный адрес статьи: http://swsys.ru/index.php?id=4471&like=1&page=article |
Версия для печати Выпуск в формате PDF (19.46Мб) |
| Статья опубликована в выпуске журнала № 2 за 2018 год. [ на стр. 382-386 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Эффективность алгоритма LU-разложения с двухмерным циклическим распределением матрицы для параллельного решения упругопластической задачи
- Реализация некоторых приложений проекта Mantevo на платформе OpenTS DMPI
- Программы моделирования температурных полей в изделиях цилиндрической формы
- Исследование производительности ряда итерационных методов решения системы линейных алгебраических уравнений в упругопластической задаче
- Разработка программного модуля для автоматического выбора решателей систем линейных алгебраических уравнений для прочностного анализа
Назад, к списку статей