Начавшийся в середине прошлого века очередной экономический кризис обусловил появление научных разработок, направленных на оптимизацию деятельности пожарной охраны и полиции, а также других органов. Так как во многих городах мира затраты на содержание охраны и полиции сокращались, возникла необходимость повысить эффективность их деятельности. В результате проведенных исследований был построен ряд моделей для обоснования минимального уровня как пожарной, так и полицейской защиты. Аналогичные исследования продолжаются до сих пор.
Остановимся на необходимом уровне пожарной защиты. Ясно, что обеспечение такого уровня лишь на настоящий момент не является полным решением задачи. Необходимо предвидеть уровень пожарной опасности на некоторое время вперед и обеспечивать соответствующую защиту с упреждением, то есть разработать методы прогнозирования пожарной опасности. Традиционно для прогнозирования временных рядов пожаров используют однофакторные линейные модели вида
yi = a + bxi + ei, (1)
где y – фактические данные пожарной статистики; x – соответствующий момент времени; a и b – оцениваемые коэффициенты; b – так называемый «тренд» модели; εi – ошибка модели; i – номер момента времени (года) [1]. Рассматриваются также линейные многофакторные модели вида
yi = a0 + a1x1i + …+ akxki + eI, (2)
где i – номер момента времени; x1, …, xk – пара- метры, с помощью которых оценивается временной ряд yi; a0, a1, …, ak – оцениваемые коэффициенты. При этом для получения модели вида (2) необходимо иметь временные ряды параметров x1, …, xk. Значения этих параметров обычно берутся из официальной статистики (Росстат, МЧС).
К сожалению, для многих объектов и явлений модели (1) и (2) не дают приемлемого описания, так как графики наблюдаемых значений результирующей переменной имеют явно криволинейное строение и не укладываются в достаточно узкую полоску на плоскости для модели (1) или не расположены в достаточной близости к гиперплоскости в модели (2).
Используются также нелинейные математические модели, где в правой части зависимости (1) помещают, помимо первых степеней некоторых параметров хi, их вторые степени и, возможно, попарные произведения [2].
Однако при взгляде на график общего числа пожаров, произошедших в какой-либо конкретной стране (в России, США или Европе) на протяжении ряда лет, заметно, что его линия совершает непериодическое волнообразное движение и не может быть удовлетворительно описана линейной зависимостью.
В такой ситуации для более точной аппроксимации статистических данных следует использовать нелинейные зависимости. Одной из самых популярных моделей, используемых в экономике на протяжении уже более 100 лет, является функция Кобба–Дугласа, моделирующая величину валового внутреннего продукта (ВВП) в зависимости от двух факторов – численности работников и оценки основных фондов объекта (страны, региона, предприятия) [3]. В экономике довольно успешно используются модели, построенные на основе так называемой производственной функции вида
 , (3)
, (3)
где Y – моделируемая величина; x1, … , xn – наблюдаемые параметры объекта [4]. С помощью моделей вида (3) довольно успешно аппроксимируют количество продукции, выпускаемой объектом исследования за определенный период времени.
Оказалось, что та же самая производственная функция (3) может достаточно успешно оценивать количество пожаров в административно-территориальной единице за определенный период времени. В частности, в качестве такой единицы можно взять всю страну. В работах [5, 6] построен ряд моделей вида
 , (4)
, (4)
где Y – общее число пожаров (в Российской Федерации или в какой-либо другой стране); Х1 – численность населения; Х2 – величина ВВП.
Отметим любопытное свойство модели (3). Если Y – оцениваемое количество продукции, выпускаемое данным объектом исследования, то в качестве параметров x1, …, xn берутся такие показатели, которые способствуют выпуску продукции. Обычно это численность работников и оценка основных фондов предприятия. Применяя эту метафору как основу для выбора модели (3) при оценке общего числа пожаров, можно считать, что пожары являются своеобразной «продукцией» социума, и для их оценки также можно использовать аналогичные показатели – численность населения (аналог числа работников предприятия) и объем основных фондов (административно-территориальной единицы).
Таким образом, в зависимости (4) под величиной Y понимается продукция объекта – страны, региона, предприятия. Практика почти столетнего моделирования показывает, что это соотношение удовлетворительно описывает зависимость выпускаемой продукции как для макро-, так и для мик- роэкономического моделирования [6]. Можно сделать предположение, что общее число пожаров, гибель людей на них, получение травм, ущерб от пожаров можно рассматривать как своего рода «продукцию» человеческого сообщества при затратах как материальных, так и человеческих ресурсов. В работе [5] зависимость (2) была применена к аппроксимации общего числа пожаров в России и США. Оказалось, что самым удивительным образом зависимость оказалась неожиданно точной – для России коэффициент корреляции с фактическими данными составляет 0,994, а для США – 0,834. Довольно любопытным оказался тот факт, что зависимость (4) очень точно отражает ди- намику общего числа пожаров для большинства стран Европы [5].
Попытаемся оценить предикторные возможности как линейной модели (2), так и производственной функции (4). Обычно производственная функция в качестве параметров использует Х1 – количество населения (млн чел.) и Х2 – основные фонды РФ (fixed assets – трлн руб.).
Используем статистические данные по населению и основным фондам РФ за 2003–2015 гг. (Росстат). Статистика пожаров приведена на сайте МЧС.
Расчет линейной модели приводит к следующей зависимости:
Y = –179,868 + 3,059×Х1 – 0,772×Х2. (5)
 Коэффициент корреляции статистических данных с оценкой по модели (5) составляет 0,991. Отметим, что коэффициент корреляции общего числа пожаров Y с оценкой основных фондов Х2 равен –0,986. Этот довольно высокий отрицательный коэффициент корреляции может навести на мысль, что при увеличении основных фондов РФ соответствующее число пожаров уменьшается, а это противоречит здравому смыслу. На рисунке 1 представлена графическая аппроксимация общего числа пожаров с помощью линейной модели (5).
Коэффициент корреляции статистических данных с оценкой по модели (5) составляет 0,991. Отметим, что коэффициент корреляции общего числа пожаров Y с оценкой основных фондов Х2 равен –0,986. Этот довольно высокий отрицательный коэффициент корреляции может навести на мысль, что при увеличении основных фондов РФ соответствующее число пожаров уменьшается, а это противоречит здравому смыслу. На рисунке 1 представлена графическая аппроксимация общего числа пожаров с помощью линейной модели (5).
Подставляя в модель (5) сведения о численности населения и объеме основных фондов за 2016 год, получаем прогноз общего числа пожаров на 2016 год:
Y = –179,868 + 3,059×146,54 – 0,772×181,62 = 128,19.
Исходя из того, что в настоящий момент статистика пожаров за 2016 год известна и общее число пожаров составляет 139,70 тыс., получаем, что ошибка прогноза на 2016 год по модели (5) составляет hлин. = (128,19 – 139,70)/139,70 % = –8,2 %.
Из представленного графика видно, что прогностическая прямая (тренд) направлена вниз и уже в 2015 году дает заниженный результат, а для 2016 года – еще более заниженный.
Рассмотрим реализацию модели (4). Ее расчет можно проводить с помощью как Microsoft Excel (надстройка «Поиск решения») [7], так и статистических пакетов (в данном случае использована программа SPSS) [8]. В результате расчета получена зависимость вида
 , (6)
, (6)
что приводит к ошибке
hлин. = (144,74 – 139,70) / 139,70 % = 3,6 %.
 На рисунке 2 представлена аппроксимация фактических данных с помощью модели (6).
На рисунке 2 представлена аппроксимация фактических данных с помощью модели (6).
Коэффициент корреляции двух временных рядов на графике рисунка 2 равен 0,988. Из рисунка 2 и расчета погрешности для нелинейной модели (6) видно, что ее возможности для прогнозирования более обоснованны.
Обратимся теперь к еще одному применению модели (4) производственной функции [9]. Здесь в качестве аппроксимируемой величины Y рассматривается полный доход гостиниц и ресторанов РФ за период с 2005 по 2014 гг. (есть официальная статистика Росстата), X1 означает численность работников гостиниц и ресторанов, Х2 – основных фондов гостиниц и ресторанов. Расчеты показывают, что модель имеет вид
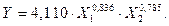 (7)
(7)
Сравнение рассчитанных по этой модели данных с фактическими представлено на рисунке 3.

Отметим хорошо наблюдаемый на графике факт – в 2010 году произошло падение выручки, что соответствует кризисному падению экономики в это время. Любопытно, что моделирующая кривая сглаживает этот скачок. Коэффициент корреляции расчетных данных с фактическими составляет 0,971, что отражает объективную динамику модели.
Поскольку модель (7) очень хорошо аппрокси- мирует данные в наблюдаемом диапазоне, ее можно использовать и как инструмент прогнозирования, то есть продолжить расчеты по данной формуле уже за пределами этого интервала.
Описанная в настоящей статье модель основана на статистических данных по Российской Федерации в целом. Аналогичные модели можно строить также и для отдельных регионов, городов, предприятий.
Таким образом, можно сделать следующие выводы.
Аппроксимация отечественной статистики имеет высокое качество (у всех построенных моделей наблюдается высокая корреляция с исходными данными).
Можно строить модели для разных уровней административно-территориальной подчиненности (для городов, их кластеров, сельской местности); при этом в качестве Х1 и Х2 следует брать соответствующие показатели (население городское, сельское, ВВП города или сельской местности и т.д.).
Поскольку такое социальное явление, как преступность, также можно рассматривать в качестве своего рода «продукции» населения и ВВП (или соответствующих их разновидностей), аналогичные расчеты следовало бы провести и для аппроксимации, и, возможно, для прогнозирования преступности.
Кроме того, было бы интересно исследовать, имеют ли содержательный смысл коэффициенты модели оценки количества пожаров.
Литература
1. Смит Г., Дрейпер Н. Прикладной регрессионный анализ. М.: Диалектика, 2016. 912 с.
2. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир, 1985. 509 с.
3. Интрилигатор И. Математические методы оптимизации и экономическая теория. М.: Айрис Пресс, 2002. 553 с.
4. Клейнер Г.Б. Производственные функции: теория, методы, применение. М.: Финансы и статистика, 1986. 354 с.
5. Пранов Б.М. О некоторых подходах к моделированию и прогнозированию временных рядов пожарной статистики // Технологии техносферной безопасности. 2014. № 5. URL: http://agps-2006.narod.ru/ttb/2014-5/23-05-14.ttb.pdf (дата обращения: 20.04.2018).
6. Leontief W. Input-output economics. Oxford Univ. Press, 1986, 436 p.
7. Мадера А.Г. Математические модели в управлении. М.: Изд-во РГГУ, 2007. 564 с.
8. Бюль А., Цефель П. SPSS: искусство обработки информации. СПб: ДиаСофтЮП, 2005. 608 с.
9. Пранов Б.М. Модели динамики и прогнозирования в сфере гостеприимства // Вестн. РМАТ. 2017. № 1. С. 24–27.
References
- Smith G., Draper N. Applied Regression Analysis. Moscow, Dialectics Publ., 2016, 912 p.
- Gill F., Murray W., Wright M. Practical Optimization. Moscow, Mir Publ., 1985, 509 p.
- Intraligator I. Mathematical Methods of Optimization and Economic Theory. Moscow, Iris Press, 2002, 576 p.
- Kleiner G.B. Production Functions: Theory, Methods, Application. Moscow, Finansy i statistika Publ., 1986, 354 p.
- Pranov B.M. Some new approach to modeling and forecasting of time series of fire statistics. Technology of Technosphere Safety. 2014, iss. 5. Available at: http://agps-2006.narod.ru/ttb/2014-5/23-05-14.ttb.pdf (accessed April 20, 2018).
- Leontief W. Input-Output Economics. Oxford, Univ. Press, 1986.
- Madera A.G. Mathematical Models in Management. Moscow, RGGU Publ., 2007, 564 p.
- Bühl A., Zöfel P. SPSS Version 10. Einfuhrung in die moderne Datenanalyse unter Windows. Pearson Studium Publ., 744 p. (Russ. ed.: St. Petersburg, DiSoftTU Publ., 2005, 608 p.).
- Pranov B.M. Dynamics and Forecasting Models in Hospitality. Vestn. RIAT. 2017, no. 1, pp. 24–27 (in Russ.).

 , (3)
, (3) , (4)
, (4)
 , (6)
, (6)
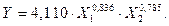 (7)
(7)