Важным источником информации о свойствах и строении нефте-, газо- и водонасыщенных пластов являются гидродинамические исследования скважин на неустановившихся режимах течения. Они позволяют определять энергетические и фильтрационно-емкостные параметры, изучать геометрию пласта и особенности его строения, вести контроль за разработкой. Для исследования околоскважинных зон пласта (десятки метров, иногда – первые сотни) используется метод восстановления давления, а межскважинного пространства – метод гидропрослушивания [1–9].
Особый интерес с точки зрения исследовательских работ и подробного изучения геологического строения представляют трещиновато-пористые коллекторы, поскольку они характеризуются высокой неоднородностью свойств и содержат сразу две системы емкостей – трещины и поры. Эти системы существенно различаются по своим свойствам, что усложняет разработку таких коллекторов. В силу некоторых особенностей трещиновато-пористых коллекторов многие стандартные методы изучения нефтяных и газовых пластов малоэффективны.
Метод двух режимов, используемый для иссле- дования скважин [3, 10–14], обычно применяется и для исследования околоскважинных зон пласта (десятки метров, иногда – первые сотни). Поскольку данный метод не требует остановки скважины (значит, нет потерь в добыче нефти), может быть исследовано большое количество добывающих скважин, что существенно повышает охват пласта исследованиями. Если при исследовании методом двух режимов разница дебитов значительна и длительность второго режима достаточна для существенного возмущения пласта, исследование можно рассматривать как аналог гидропрослушивания и, регистрируя давление на забое соседних скважин, исследовать межскважинную зону.
В связи с этим представляет интерес изучение способов интерпретации гидродинамических исследований межскважинного пространства трещиновато-пористых коллекторов методом двух режимов, в том числе с помощью численных моделей.
Математическая модель. Решение прямой задачи
Для решения прямой задачи запишем математическую модель, описывающую фильтрацию флюида при гидродинамических исследованиях меж- скважинного пространства для любой геометрии пласта, расстановки и количества скважин, распределения свойств пласта по площади. Такая модель может быть только численной. Рассмотрим границы применимости описываемой математической модели фильтрации флюида в продуктивном пласте:
- фильтрация однофазная;
- жидкость слабосжимаемая;
- пласт упругий;
- гравитационными силами можно пренебречь;
- продуктивный пласт содержит поры и трещины;
- проницаемость трещин значительно больше проницаемости пор;
- пористость трещин значительно меньше пористости пор;
- участки пористой матрицы не обмениваются между собой флюидом;
- к скважине приток происходит только по трещинам;
- при снижении давления поры матрицы отдают флюид в трещины;
- в начальный момент времени матрица и трещины находятся в равновесии, перетоки отсутствуют;
- поток из матрицы в трещину установившийся, поэтому матрицу можно рассматривать как одну ячейку в одном блоке сетки.
Тогда уравнения сохранения объема флюида в поверхностных условиях отдельно для трещин и пор можно записать соответственно как
 , (1)
, (1)
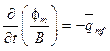 , (2)
, (2)
где нижние индексы f и m означают трещины и пористую матрицу соответственно; f – пористость; B – объемный коэффициент флюида;  – вектор скорости фильтрации;
– вектор скорости фильтрации;  – плотность потока в скважину;
– плотность потока в скважину; 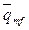 – плотность перетока из пор матрицы в трещины [1, 2, 4, 15–17].
– плотность перетока из пор матрицы в трещины [1, 2, 4, 15–17].
Скорость фильтрации определяется через закон Дарси:
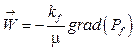 , (3)
, (3)
где kf – проницаемость трещин; m – вязкость флюида; Pf – давление в трещинах.
Уравнения (1)–(3) дополняются начальными условиями, граничными условиями и замыкающими соотношениями:
 , (4)
, (4)
 , (5)
, (5)
 , (6)
, (6)
где ff0, fm0 и B0 – пористость трещин, пористость матрицы и объемный коэффициент флюида соответственно при начальном давлении P0; Crf, Crm и Cl – сжимаемость трещин, пор и флюида соответственно.
Кроме замыкающих соотношений (4)–(6), необходимо задать источниковые члены в уравнениях (1) и (2). Поскольку поток из матрицы в трещину установившийся, его можно задать как
 , (7)
, (7)
где 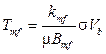 ,
,
 ,
,
 ,
, 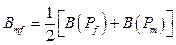 ,
,
Tmf – коэффициент трещинно-поровой проводи- мости; σ – фактор формы (шейп-фактор); Vb – элементарный объем пласта; kmx, kmy, kmz и kfx, kfy, kfz – проницаемость пор и трещин вдоль осей X, Y, Z декартовой системы координат; n – параметр формы элемента (блока) пористой матрицы (n = 1 – плита, n = 2 – призма или цилиндр, n = 3 – куб или сфера);  – характерный размер блоков матрицы [1, 2, 4, 15–17].
– характерный размер блоков матрицы [1, 2, 4, 15–17].
Приток флюида (источниковое слагаемое) к вертикальной скважине в псевдоустановившемся приближении [18] запишется как
 , (8)
, (8)
где  ,
,  ,
,
heff – эффективная толщина пласта; Rc – радиус контура питания; rwell – радиус скважины; Skin – скин-фактор скважины.
Вычислим радиус контура питания для прямоугольной конечно-разностной вычислительной сетки:
 ,
,
где i и j – индексы ячейки сетки вдоль осей X и Y соответственно; Δx и Δy – размеры ячейки вдоль осей X и Y соответственно.
Уравнения (1) и (2) с учетом (4)–(6) можно пе- реписать в виде
 , (9)
, (9)
 . (10)
. (10)
Запишем конечно-разностный аналог уравнения (9) для трещиноватой среды. Фильтрация двумерная, в горизонтальной плоскости. Численная схема – «классики». Неявное уравнение для давления в трещинах:
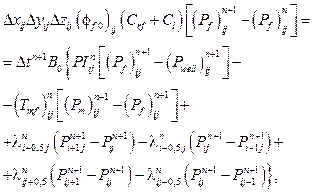 (11)
(11)
где Dtn+1 – переменный шаг по времени, определяемый в соответствии с рекомендациями [18] так, чтобы максимальное по всем блокам сетки изменение давления не превышало заданного значения (при расчетах отдельно задавалось предельное изменение давления в матрице и в трещинах),
 ,
,
 ,
,
 ,
,
 ,
,
аналогично для  ,
, 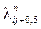 и
и  .
.
Явное уравнение для давления в трещинах:
 (12)
(12)
Название «классики» для разностной схемы связано со способом обхода расчетных точек [19]. На каждом шаге по времени n + 1 обход точек пространственной сетки в одной (в нашем случае горизонтальной) плоскости совершается дважды. На первом и последующих шагах по времени с нечетным n + 1 вычисляются значения давления в ячейках с нечетной суммой i + j. Этот первый обход осу- ществляется с помощью явной по давлению схемы. При втором обходе на том же шаге по времени вычисляют значения давления в ячейках с четной суммой i + j с помощью неявной по давлению схемы, в соседних ячейках берутся значения давления, полученные на том же шаге по времени при первом обходе. На втором и последующих шагах по времени с четными n + 1 роли узлов с четной и нечетной суммой i + j меняются. Кратко это можно резюмировать так: при i + j + n + 1 четном берется уравнение (12), а при нечетном – уравнение (11).
Запишем конечно-разностный аналог уравнения (10) для давления в пористой матрице:
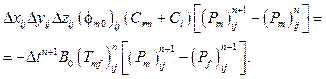 (13)
(13)
Из (13) можно легко выразить давление в матрице на новом временном шаге  через давление в трещинах
через давление в трещинах  :
:
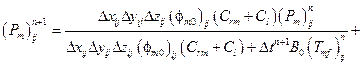
 . (14)
. (14)
Подставляя (14) в (11) и (12), исключаем из них неизвестное давление в матрице на новом шаге по времени  .
.
При расчете перетоков (7) для плоского случая 2D-геометрии будем считать  ,
,  , где αmz – коэффициент вертикальной анизотропии проницаемости пористой матрицы.
, где αmz – коэффициент вертикальной анизотропии проницаемости пористой матрицы.
Решение обратной задачи
Интерпретация гидродинамических исследований скважин сводится к совмещению расчетной и фактической кривых давления (или дебита) путем изменения параметров модели. Цель – получение наилучшего совмещения и определение параметров модели: фильтрационно-емкостных и (если такие есть) геометрических характеристик пласта. Таким образом, интерпретация гидродинамических исследований скважин сводится к обратной задаче, решаемой методами теории оптимизации. Рассмотрим один из методов решения такой зада- чи – метод Ньютона.
Пусть необходимо найти минимум функции многих переменных f(X), где X = (x1, x2, …, xn). В данном случае функция f(X) – это невязка между расчетными и фактическими точками давления, замеренного на забое скважины. Эта задача эквива- лентна задаче нахождения значений X, при которых градиент функции f(X) равен нулю:
grad(f(X)) = 0. (15)
Применим к (15) метод Ньютона:
grad(f(X j)) + H(X j)(X j+1 –X j) = 0, (16)
где j = 1, 2, 3, …, m – номер итерации; H(X) – гессиан функции f(X).
Напомним, что гессиан функции – это симметричная квадратичная форма, описывающая поведение функции во втором порядке:
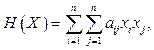
где aij = ¶2f /¶xi¶xj; функция f(X) задана на n-мерном пространстве вещественных чисел.
В более удобном для вычислений виде формулу (16) можно представить как
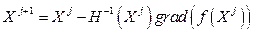 .
.
Метод Ньютона прост в реализации, но нахождение матрицы Гессе сопряжено с большими вычислительными затратами из-за необходимости нахождения большого количества частных производных. Однако ввиду некоторой простоты модели, принятой для решения прямой задачи, использование метода Ньютона вполне оправдано и дает приемлемое время счета.
Пример интерпретации гидродинамических исследований межскважинного пространства трещиновато-пористого коллектора методом двух режимов с помощью описанной модели
Для проверки описанной модели в качестве фактических данных будем использовать значения давления, полученные путем численного моделирования на сетке Вороного с помощью коммерческой программы для интерпретации гидродинамических исследований скважин и пластов Saphir компании Kappa Engineering [5].
 Геометрия рассматриваемой модели и расстановка скважин приведены на рисунке 1. Модель содержит три скважины. Две добывающие (возмущающие) скважины по очереди исследуются методом двух режимов (путем однократного изменения режима работы, то есть дебита [3, 10–14]). В третьей (реагирующей) скважине фиксируется изменение забойного давления в результате работы первых двух скважин. Все время исследования составляет 30 суток. Одна возмущающая скважина эксплуатируется 10 суток с дебитом 300 м3/сут., затем 20 суток с дебитом 100 м3/сут. Другая возмущающая скважина эксплуатируется 20 суток с дебитом 300 м3/сут., затем 10 суток с дебитом 100 м3/сут.
Геометрия рассматриваемой модели и расстановка скважин приведены на рисунке 1. Модель содержит три скважины. Две добывающие (возмущающие) скважины по очереди исследуются методом двух режимов (путем однократного изменения режима работы, то есть дебита [3, 10–14]). В третьей (реагирующей) скважине фиксируется изменение забойного давления в результате работы первых двух скважин. Все время исследования составляет 30 суток. Одна возмущающая скважина эксплуатируется 10 суток с дебитом 300 м3/сут., затем 20 суток с дебитом 100 м3/сут. Другая возмущающая скважина эксплуатируется 20 суток с дебитом 300 м3/сут., затем 10 суток с дебитом 100 м3/сут.
Основные исходные данные для расчетов следующие:
- радиус скважины – 0,1 м;
- толщина пласта – 10 м;
- расстояние между возмущающими и реаги- рующей скважинами – 500 м;
- объемный коэффициент – 1,1 м3/м3;
- вязкость – 1,3 мПа·с;
- общая сжимаемость – 4,3·10-5 см2/кгс;
- начальное пластовое давление – 250 кгс/см2.
 Тензор проницаемости трещиноватой породы диагональный. Проницаемость трещинной части пласта зависит от направления фильтрации. Оси расчетной сетки сориентированы по осям тензора проницаемости. Сетка неравномерная, размеры ячеек по оси Х приведены на рисунке 2. По оси Y размеры ячеек аналогичны. Реагирующая скважина находится в ячейке с координатами 120–120, которая имеет размеры 0,1´0,1 м. Поскольку по формуле (8) невозможно определить забойное давление при нулевом дебите, в качестве забойного давления в реагирующей скважине принято давление в ячейке, которую она занимает. Поэтому приняты столь малые размеры ячейки.
Тензор проницаемости трещиноватой породы диагональный. Проницаемость трещинной части пласта зависит от направления фильтрации. Оси расчетной сетки сориентированы по осям тензора проницаемости. Сетка неравномерная, размеры ячеек по оси Х приведены на рисунке 2. По оси Y размеры ячеек аналогичны. Реагирующая скважина находится в ячейке с координатами 120–120, которая имеет размеры 0,1´0,1 м. Поскольку по формуле (8) невозможно определить забойное давление при нулевом дебите, в качестве забойного давления в реагирующей скважине принято давление в ячейке, которую она занимает. Поэтому приняты столь малые размеры ячейки.
При интерпретации гидродинамических исследований трещиновато-пористых пластов используются следующие специфические параметры:  ,
,  , где λ – параметр, характеризующий перетоки между матрицей и трещинами; ω – отношение емкости трещин к общей емкости системы; h – толщина пласта; Ct – суммарная сжимаемость пласта и флюида [1, 2, 4, 15–17].
, где λ – параметр, характеризующий перетоки между матрицей и трещинами; ω – отношение емкости трещин к общей емкости системы; h – толщина пласта; Ct – суммарная сжимаемость пласта и флюида [1, 2, 4, 15–17].
При этом из параметра перетоков λ обычно определяют проницаемость матрицы km либо фак- тор формы σ (по которому судят о размерах блоков матрицы), а из отношения емкостей ω – пористость трещин ff. Как правило, эти параметры имеют наибольшую степень неопределенности.
Рассмотрены три варианта интерпретации исследования с различным количеством уточняемых параметров.
1. Проницаемость трещин kf, пористость матрицы fm, отношение емкостей ω, параметр перетоков λ, анизотропия проницаемости трещин по площади (kx/ky)f.
2. Отношение емкостей ω, параметр перетоков λ.
3. Проницаемость трещин kf, пористость матрицы fm, анизотропия проницаемости трещин по площади (kx/ky)f.
Выбор уточняемых параметров обусловлен наибольшей неопределенностью в указанных параметрах, возникающей при анализе промысловых данных.
Результаты интерпретации приведены в таблице. Видно, что наилучшее качество уточнения дает третья группа параметров, а наихудшее – первая, чего и следовало ожидать, так как параметры ω и λ незначительно влияют на показания давления в реагирующей скважине при больших временах [1, 16, 17], а большое количество параметров (первая группа) почти всегда плохо поддается уточнению при решении обратных задач методами теории оптимизации.

В качестве примера на рисунке 3 приведены результаты интерпретации для первого начального приближения.

Заключение
Рассмотрен подход к интерпретации гидродинамических исследований межскважинного пространства трещиновато-пористых коллекторов методом двух режимов с помощью численных моделей. Приведена оригинальная конечно-разностная схема.
Рассмотрено несколько вариантов интерпретации для различных наборов уточняемых пара- метров. Подтверждено, что параметры ω (относительная емкость трещин) и λ (параметр перетока матрица–трещины) мало влияют на показания давления в реагирующей скважине при больших временах.
Поэтому в качестве определяемых параметров рекомендуется выбирать проницаемость трещин, пористость матрицы и анизотропию проницаемости трещин по площади. Использовать в качестве определяемых параметров сразу все пять не рекомендуется.
Работа выполнена при поддержке Программы фундаментальных научных исследований государственных академий наук № I.2.П27, заказ № 18-0111_П, НИР № 0065-2018-0111.
Литература
1. Деева Т.А., Камартдинов М.Р., Кулагина Т.Е., Мангазеев П.В. Гидродинамические исследования скважин: анализ и интерпретация данных. Томск: Изд-во ЦППС НД ТПУ, 2009. 243 с.
2. Кульпин Л.Г., Мясников Ю.А. Гидродинамические методы исследования нефтегазоводоносных пластов. М.: Недра, 1974. 200 с.
3. Эрлогер Р. мл. Гидродинамические методы исследования скважин. М.–Ижевск: Изд-во ИКИ, 2007. 512 с.
4. Bourdet D. Well Test analysis: the use of advanced interpretation models. Amsterdam: Elsevier Sc. B.V., 2002, 425 p.
5. Houze O., Viturat D., Fjaere O.S. Dynamic data analysis. V 5.12. Kappa Engineering, 2017, 743 p.
6. Vela S., McKinley R.M. How areal heterogeneities affects pulse-test results. Soc. Pet. Eng. J., 1970, no. 2, pp. 181–191.
7. Jahns Hans O. Rapid method for obtaining a two-dimen- sional reservoir description from well pressure response data. Soc. Pet. Eng. J., 1966, no. 4, pp. 315–327.
8. McKinley R.M., Vela S., Carlton L.A. A field application of pulse-testing for detailed reservoir description. JPT, 1968, vol. 20, no. 3, pp. 313 – 321.
9. Woods E.G. Pulse-test response of a two-zone reservoir. Soc. Pet. Eng. J., 1970, vol. 10, no. 3, pp. 245–256.
10. Афанаскин И.В., Вольпин С.Г., Ломакина О.В., Штейнберг Ю.М. Гидродинамические исследования вертикальных скважин в пластах с двумя границами методом двух режимов // Вестн. кибернетики. 2017. № 4. С. 45–54.
11. Афанаскин И.В., Вольпин С.Г., Штейнберг Ю.М., Ломакина О.В. Гидродинамические исследования горизонтальных скважин методом двух режимов // Вестн. кибернетики. 2017. № 2. С. 108–113.
12. Афанаскин И.В., Крыганов П.В., Вольпин С.Г., Штейнберг Ю.М., Вольпин И.А. Изучение свойств нефтяных пластов с помощью гидродинамических исследований скважин методом двух режимов – теория, моделирование и практика // Вестн. кибернетики. 2015. № 3. С. 86–107.
13. Афанаскин И.В., Крыганов П.В., Вольпин С.Г., Штейнберг Ю.М., Вольпин И.А. Оценка фильтрационных и энергетических параметров нефтяных пластов с помощью гидродинамических исследований скважин на двух режимах: теория, моделирование и практика // Тр. НИИСИ РАН. 2015. Т. 5. № 1. С. 41–55.
14. Russell D.G. Determination of formation characteristics from two rate flow test. JPT, 1963, vol. 15, pp. 1317–1355.
15. Бурде Д. Интерпретация результатов исследований скважин // Petroleum Engineering and Related Management Traning Gubkin Academy: матер. лекций. М., 1994. 109 с. (рус.).
16. Гольф-Рахт Т.Д. Основы нефтепромысловой геологии и разработки трещиноватых коллекторов. М.: Недра, 1986. 608 с.
17. Райс Л. Основы разработки трещиноватых коллекторов. М.–Ижевск: Из-во ИКИ, 2012. 118 с.
18. Азиз Х., Сеттари Э. Математическое моделирование пластовых систем. М.–Ижевск: Изд-во ИКИ, 2004. 416 с.
19. Роуч П. Вычислительная гидродинамика. М.: Мир, 1980. 616 с.
References
- Deeva T.A., Kamartdinov M.R., Kulagina T.E., Mangazeev P.V. Well Test: Data Analysis and Interpretation. Tomsk, TsPPS ND TPU Publ., 2009, 243 p.
- Kulpin L.G., Myasnikov Yu.A. Investigation of Oil and Gas Reservoirs by Hydrodynamic Methods. Moscow, Nedra Publ., 1974, 200 p.
- Erloger R. jr. Advances in Well Test Analysis. Moscow–Izhevsk, IKI Publ., 2007, 512 p.
- Bourdet D. Well Test Analysis: The Use of Advanced Interpretation Models. Amsterdam, Elsevier Science B.V. Publ., 2002, 425 p.
- Houze O., Viturat D., Fjaere O.S. Dynamic Data Analysis. V 5.12. Kappa Engineering Publ., 2017, 743 p.
- Vela Saul, McKinley R.M. How areal heterogeneities affects pulse-test results. Soc. Pet. Eng. J. 1970, pp. 181–191.
- Jahns Hans O. Rapid method for obtaining a two-dimensional reservoir description from well pressure response data. Soc. Pet. Eng. J. 1966, pp. 315–327.
- McKinley R.M., Vela Saul, Carlton L.A. A field application of pulse-testing for detailed reservoir description. J. Pet. Tech. 1968, pp. 313–321.
- Woods E.G. Pulse-test response of a two-zone reservoir. Soc. Pet. Eng. J. 1970, pp. 245–256.
- Afanaskin I.V., Volpin S.G., Lomakina O.V., Shteynberg Yu.M. Two-rate tests of vertical wells in formations with two boundaries. Proc. in Cybernetics. 2017, no. 4, pp. 45–54 (in Russ.).
- Afanaskin I.V., Volpin S.G., Shteynberg Yu.M., Lomakina O.V. Two-rate tests of horizontal wells. Proc. in Cybernetics. 2017, no. 2, pp. 108–113 (in Russ.).
- Afanaskin I.V., Kryganov P.V., Volpin S.G., Shteynberg Yu.M., Volpin I.A. Oil-bearing formations characterization by two-rate well tests results – theory, modeling and practice. Proc. in Cybernetics. 2015, no. 3, pp. 86–107 (in Russ.).
- Afanaskin I.V., Kryganov P.V., Volpin S.G., Shteynberg Yu.M., Volpin I.A. Evaluation of oil-bearing formation flow and energy parameters by two-rate well tests results – theory, modeling and practice. SRISA RAS Proc. 2015, vol. 5, no. 1,
pp. 41–55 (in Russ.).
- Russell D.G. Determination of formation characteristics from two rate flow test. J. Pet. Tech. 963, pp. 1347–1355.
- Burde D. Interpretation of well test. Proc. Petroleum Engineering and Related Management Traning Gubkin Academy. Moscow, 1994, 109 p.
- Golf-Rakht T.D. Fundamental of Fractured Reservoir Engineering. Moscow, Nedra Publ., 1986, 608 p.
- Rays L. Fundamentals of the Fractured Reservoirs Development. Moscow–Izhevsk, IKI Publ., 2012, 118 p.
- Aziz Kh., Settari E. Petroleum Reservoir Simulation. Moscow–Izhevsk, IKI Publ., 2004, 416 p.
- Rouch P. Computational Fluid Dynamics. Moscow, Mir Publ., 1980, 616 p.



 , (1)
, (1)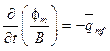 , (2)
, (2) – вектор скорости фильтрации;
– вектор скорости фильтрации;  – плотность потока в скважину;
– плотность потока в скважину; 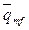 – плотность перетока из пор матрицы в трещины [1, 2, 4, 15–17].
– плотность перетока из пор матрицы в трещины [1, 2, 4, 15–17].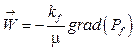 , (3)
, (3) , (4)
, (4) , (5)
, (5) , (6)
, (6) , (7)
, (7)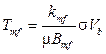 ,
, ,
, ,
, 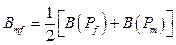 ,
, – характерный размер блоков матрицы [1, 2, 4, 15–17].
– характерный размер блоков матрицы [1, 2, 4, 15–17]. , (8)
, (8) ,
,  ,
, ,
, , (9)
, (9) . (10)
. (10)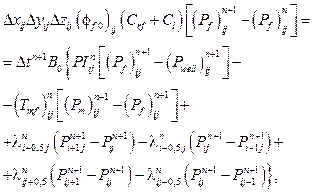 (11)
(11) ,
, ,
, ,
, ,
, ,
, 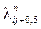 и
и  .
. (12)
(12)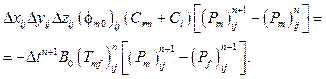 (13)
(13) через давление в трещинах
через давление в трещинах  :
: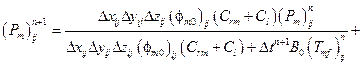
 . (14)
. (14) ,
,  , где αmz – коэффициент вертикальной анизотропии проницаемости пористой матрицы.
, где αmz – коэффициент вертикальной анизотропии проницаемости пористой матрицы.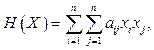
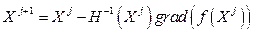 .
.

 ,
,  , где λ – параметр, характеризующий перетоки между матрицей и трещинами; ω – отношение емкости трещин к общей емкости системы; h – толщина пласта; Ct – суммарная сжимаемость пласта и флюида [1, 2, 4, 15–17].
, где λ – параметр, характеризующий перетоки между матрицей и трещинами; ω – отношение емкости трещин к общей емкости системы; h – толщина пласта; Ct – суммарная сжимаемость пласта и флюида [1, 2, 4, 15–17].

