Оптимизация обработки информационных запросов в СУБД
| Голенищев Э.П. () - , Дербанов С.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
С внедрением во все сферы профессиональной деятельности человека автоматизированных информационных систем (АИС), призванных повысить производительность труда или эффективность выполнения должностных обязанностей, повышается актуальность исследований, посвященных поиску высокоэффективных алгоритмов обработки информационных запросов к базам данных (БД), составляющих основу АИС [1,2]. Известно множество различных способов выполнения сложных запросов, поэтому одной из важнейших задач теории обработки запросов является определение наиболее эффективного из них. В первых поколениях БД низкоуровневый язык обработки запросов обычно встраивался в какой-либо из высокоуровневых языков программирования. В этом случае вся ответственность за выбор оптимальной стратегии обработки запросов возлагалась на программиста. При использовании современных декларативных языков, например SQL, пользователь должен только определить, какие данные ему нужны, не указывая на то, как эти данные могут быть получены. В результате от пользователя АИС не требуется каких-либо знаний о существующих стратегиях обработки запросов; перенос ответственности за выбор оптимальной стратегии обработки запросов на систему управления базами данных (СУБД) предотвращает выбор пользователем заведомо неэффективных стратегий и предоставляет СУБД больше возможностей контролировать общую производительность всей системы. По результатам проведенного анализа выявлено два основных метода обработки запросов (на практике чаще используется их комбинация). Первый метод для определения порядка выполнения запроса предполагает использование эвристических правил [2]. Второй метод заключается в сравнительной оценке стоимости различных вариантов выполнения запроса и выборе того варианта, который предполагает минимальное использование ресурсов [5,6]. Поскольку скорость доступа к данным на диске невелика, в качестве основного показателя оценки стоимости выполнения запроса обосновано использовать количество (время, стоимость) дисковых операций [2]. Целесообразно проанализировать последовательность основных этапов обработки запросов СУБД, представленную на рисунке.
В условиях ограничений, определяемых требованиями пользователей ко времени реакции системы, возникает следующая экстремальная задача: путем декомпозиции и выбора метода оптимизации, автоматической генерации кода СУБД необходимо представить пользователю результаты выполнения корректного информационного запроса пользователю за наименьшее время с учетом имеющихся системных ресурсов. Выделим основные частные задачи: - проверка корректности пользовательского запроса; - обоснование и выбор метода оптимизации запроса в зависимости от временных и ресурсных ограничений; - оптимальное распределение функций компиляции между программной и аппаратной частями АИС. Первые две задачи предлагается свести к известной задаче о наименьшем покрытии (ЗНП) [3,4,7]. ЗНП своим названием обязана следующей теоретико-множественной интерпретации. Даны множество R={r1, …, rM} и семейство Á={S1, …, SN} множеств SjÌR. Любое подсемейство Á¢={Sj1, Sj2,…, Sjk} семейства Á такое, что Если каждому SjÎÁ поставлена в соответствие положительная стоимость cj, то необходимо найти покрытие множества R, имеющее наименьшую стоимость, причем стоимость семейства Á¢={Sj1, Sj2,…, Sjk} определяется как В матричной форме, когда строки (M´N)-матрицы [tij], состоящей из нулей и единиц, покрываются столбцами, ЗНП может быть сформулирована аналогично задаче линейного программирования: минимизировать при ограничениях где cj³0, При исследовании решаемой задачи удалось сделать следующие выводы и упрощения. 1. Если для некоторого элемента ri из R справедливы соотношения riÏSj "j=1,…,N, то ri покрыть нельзя и, следовательно, задача не имеет решения (некорректно сформулирован запрос). 2. Если $riÎR такое, что riÎSk и riÏSj, "j¹k, то Sk должно присутствовать во всех решениях и задачу можно свести к «меньшей», положив R=R-{ri} и Á=Á-{Sk}. 3. Пусть Vi={j½ riÎSj}; тогда если $p, qÎ{1, …, M} такие, что VpÍVq, то rq можно удалить из R, поскольку любое множество, которое покрывает rp, должно также покрывать rq, то есть rp доминирует над rq. 4. Если для некоторого семейства множеств`ÁÌÁ справедливы соотношения Когда все упрощения выполнены (если они возможны) и исходная задача переформулирована в соответствующей неприводимой форме, наступает этап ее решения. В качестве R целесообразно рассматривать запрос, сформулированный пользователем АИС, а в качестве Á – семейство операций реляционной алгебры (РА) [1,5]. Запрос R будет выполнен за наименьшее время, если он будет представлен совокупностью операций реляционной алгебры, в сумме имеющих наименьшую стоимость. В свою очередь, вопрос определения стоимостей различных операций РА может решаться на основе статистической информации, накапливаемой службами современных СУБД. Так, типичная СУБД сохраняет в своем системном каталоге следующие статистические данные [2]. 1. Для каждого базового отношения X: ntuples(X) – количество кортежей в отношении X (то есть его кардинальность); bfactor(X) – показатель блокирования отношения X (то есть количество кортежей отношения Х, размещаемых в одном дисковом блоке); nblocks(X) – количество блоков вторичной памяти, необходимых для сохранения отношения Х. Если кортежи отношения Х физически размещаются на одном участке, то справедлива формула: nblocks(X)= [ntuples(X)/ bfactor(X)]. 2. Для каждого атрибута А базового отноше- ния Х: ndistinctA(X) – количество уникальных значений атрибута А в отношении Х; minA(X), maxA(X) – минимальное и максимальное количество возможных значений атрибута А в отношении Х; SCA(X) – кардинальность выборки атрибута А в отношении Х. Оно представляет собой среднее количество кортежей, которые удовлетворяют условию, заданному для атрибута А. В предположении, что значения атрибута А равномерно распределены по отношению Х и что существует по крайней мере одно значение, удовлетворяющее заданному условию, SCA(X) может принимать значения: 1 – если атрибут А является ключевым для отношения Х, и [ntuples(X)/ndistinctA(X)] – в противном случае. Кроме того, может быть выполнена оценка кардинальности выборки для различных условий. В этом случае значение SCA(X) может быть определено по следующим соотношениям: а) для А>q: [ntuples(X)*( maxA(X)-q)/(maxA(X)-minA(X))], б) для А [ntuples(X)*(q-maxA(X))/(maxA(X)-minA(X))], в) для АÎ{q1, q2, …, qn}: [(ntuples(X)/ndistinctA(X))*n], г) для АÚB: SCA(X)*SCB(X), д) для АÙB: SCA(X)*SCB(X)-SCA(X)-SCB(X). 3. Для каждого атрибута многоуровневого индекса I множества значений атрибута А: nlevelsA(I) – количество уровней индекса I; nlfblocksA(I) – количество листовых блоков индекса I. Конечно, поддержание всех этих статистических показателей в актуальном состоянии может представлять собой серьезную проблему. Так, если СУБД будет выполнять их обновление каждый раз при вставке, удалении или обновлении кортежа, то это скажется отрицательно на производительности системы. Процедуры обновления статистики целесообразно выполнять либо в моменты простоя системы, либо с установленным периодом. Накопление результатов многократного решения поставленной задачи может способствовать выработке или уточнению эвристических правил оптимизации запросов. Таким образом, постановка задачи оптимизации запросов в реляционных СУБД возможна в терминах линейного или целочисленного программирования. Список литературы 1. Голенищев Э.П., Клименко И.В. Информационные обеспечение систем управления. – Р-н-Д: Феникс, 2003. – 352с. 2. Коннолли Т., Бегг К., Страчан А. Базы данных: проектирование, реализация и сопровождение. Теория и практика. 2-е изд. /Пер. с англ. – М.: Издат. дом «Вильямс», 2000. – 1120с. 3. Кофман А. Введение в прикладную комбинаторику. – М.: Наука, 1975. – 480с. 4. Кристофидес Н. Теория графов. Алгоритмический подход. – М.: Мир, 1978. – 432с. 5. Мейер Д. Теория реляционных баз данных. / Пер. с англ. – М.: Мир, 1987. – 608с. 6. Озкарахан Э. Машины баз данных и управление базами данных. / Пер. с англ. – М.: Мир, 1989. – 696с. 7. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность / Пер. с англ. – М.: Мир, 1985. – 512с. |
http://swsys.ru/index.php?id=450&lang=%29&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Схемотехнические САПР для персональных компьютеров
- Интеллектуальный анализ данных и реализация моделей портфельного анализа в среде MS Excel
- Инструментальные и программные средства построения сетевых моделей
- Прогнозирование эффективности систем хранения информации
- Основы интеллектуальной информационной технологии обеспечения безопасности производства

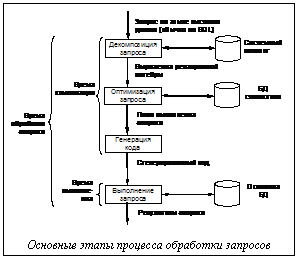 Время обработки запросов в общем случае складывается из времен его компиляции и выполнения. Сокращение любой из этих составляющих должно уменьшать общее время обработки запроса, но интуитивно понятно, что между ними должна существовать зависимость. Так, можно предположить, что чем больше времени отводится на компиляцию, тем выше вероятность получения оптимального плана, следовательно, запрос выполняется за наименьшее время.
Время обработки запросов в общем случае складывается из времен его компиляции и выполнения. Сокращение любой из этих составляющих должно уменьшать общее время обработки запроса, но интуитивно понятно, что между ними должна существовать зависимость. Так, можно предположить, что чем больше времени отводится на компиляцию, тем выше вероятность получения оптимального плана, следовательно, запрос выполняется за наименьшее время. является покрытием множества R, а множества Sji являются покрывающими множествами.
является покрытием множества R, а множества Sji являются покрывающими множествами. .
.
 i=1, 2, …, M,
i=1, 2, …, M, и
и 
 и
и  для любых SkÎÁ-`Á, то Sk может быть вычеркнуто из Á, поскольку
для любых SkÎÁ-`Á, то Sk может быть вычеркнуто из Á, поскольку  доминирует над Sk.
доминирует над Sk.