Подавляющее большинство оптимизационных задач, решаемых в процессе конструкторского этапа автоматизированного проектирования элементов электронно-вычислительной аппаратуры (ЭВА), требуют огромных затрат времени и вычислительных ресурсов. Это обусловлено необходимостью перебора огромного числа различных вариантов решений. При этом по своей вычислительной сложности задачи проектирования относятся к классу так называемых NP-полных задач, то есть задач, для которых не существует детерминированного полиномиального алгоритма.
Следовательно, для гарантированного нахождения наилучшего решения (глобального экстремума) в таких задачах требуется выполнить полный перебор, что в реальности не представляется возможным в силу их большой размерности [1–4]. Поэтому на практике для решения такого рода задач разрабатываются различные метаэвристические алгоритмы, позволяющие находить близкие к оптимальным (квазиоптимальные) решения.
Одним из подходов, позволяющих успешно решать задачу повышения эффективности и качества решения сложных оптимизационных задач большой размерности, является интеграция различных научных методов, характерных для таких направлений вычислительного интеллекта, как биоинспирированные алгоритмы, нечеткие вычисления, искусственные нейронные сети [5–8].
В научной литературе описано большое количество различных модификаций генетических алгоритмов для решения широкого круга задач конструкторского этапа проектирования [5–8]. Как правило, такие алгоритмы достаточно успешно справляются с задачей нахождения квазиоптимального решения за полиномиальное время. Однако большинство упомянутых выше алгоритмов имеют проблемы с преждевременной сходимостью процесса поиска. Также при организации генетических алгоритмов важно учитывать необходимость расширения области поиска, возможность организации поиска в различных удаленных друг от друга областях пространства допустимых решений.
В данной статье предлагается гибридный подход к решению рассматриваемых оптимизационных задач на основе интеграции таких подходов, как эволюционные алгоритмы поиска, искусственные нейронные сети, нечеткие модели управления параметрами алгоритма и механизмы распараллеливания вычислений для повышения эффективности организации процесса поиска [9–19].
Постановка задачи
К конструкторскому этапу проектирования ЭВА относятся задачи компоновки, размещения, трассировки, планирования, верификации. Наиболее сложными и ответственными с точки зрения качества будущих изделий являются задачи размещения и трассировки. Кроме того, эти задачи тесно связаны между собой, поскольку результат ре- шения задачи размещения элементов является исходной информацией для задачи трассировки, а качество решения задачи размещения непосредственно влияет на сложность и качество задачи трассировки. Поэтому представляет практический интерес разработка интегрированных методов, позволяющих решать эти задачи в едином цикле с учетом взаимных ограничений и текущих результатов [20, 21].
Пусть задано множество элементов E = {ei | i = = 1, …, N}, где ei – размещаемый элемент; N – количество размещаемых элементов. Здесь ei = (li, hi, Ti), где li – длина элемента; hi – высота элемента; Ti – список контактов элемента размещения, Ti = {tj | j = 1, …, K}, где tj – контакт, K – количество контактов элемента, причем tj = (xj, yj), где xj, yj – координаты контакта относительно базовой точки элемента.
Множество соединяющих элементы цепей U = ={uh | h = 1, …, L}, где uh – цепь, L – количество цепей; uh = {(Nek, Nck) | k = 1, …, M}, Nek – номер элемента, Nck – номер контакта, M – количество контактов, соединяемых цепью.
Необходимо найти вариант размещения элементов на монтажном пространстве: V = {(xi, yi) | i = 1, …, N}, где (xi, yi) – координаты верхнего левого угла установочной площади элемента размещения i, такие, чтобы суммарная площадь перекрытия размещенных элементов была равна нулю, а сумма значений остальных критериев минимальна.
Для каждой цепи следует найти список позиций коммутационного поля, через которые она проходит: Wh = {(xq, yq) | i = 1, …, Q}, где Q – количество позиций, через которые проходит h-я цепь.
Описание алгоритма
Кодирование пространства решений задачи. При кодировании решений множество позиций представляется в виде регулярной структуры (решетки). Каждая позиция pi имеет координаты xi, yi. Позиции нумеруются по возрастанию координаты xi в пределах строки слева направо, а строки, в свою очередь, упорядочиваются по возрастанию коорди- наты yi сверху вниз.
 Каждый элемент имеет базовую точку Odi и базовые оси координат OdiXdi, OdiYdi, относительно которых задается контурное описание элемента ei. Базовой точкой является нижний левый угол элемента. Контурное описание имеет прямоугольную форму. Будем считать, что элемент ei назначен в позицию pj, если его базовая точка Odi совмещена с точкой коммутационного поля, имеющей координаты xj, yj. Точки пересечения пунктирных линий соответствуют посадочным позициям на коммутационном поле (рис. 1).
Каждый элемент имеет базовую точку Odi и базовые оси координат OdiXdi, OdiYdi, относительно которых задается контурное описание элемента ei. Базовой точкой является нижний левый угол элемента. Контурное описание имеет прямоугольную форму. Будем считать, что элемент ei назначен в позицию pj, если его базовая точка Odi совмещена с точкой коммутационного поля, имеющей координаты xj, yj. Точки пересечения пунктирных линий соответствуют посадочным позициям на коммутационном поле (рис. 1).
Каждое решение представляется в виде хромосомы Hi. Порядковый номер гена в хромосоме соответствует порядковому номеру размещаемого элемента. Значение гена соответствует номеру позиции на коммутационном поле. Число генов в хромосоме равно количеству размещаемых элементов.
Определение целевой функции (ЦФ) задачи. При расчете значения ЦФ размещения вычисляются нормированная оценка суммы штрафа за перекрытие площадей размещаемых элементов, оценки длин межсоединений, показателя трассируемости, а также оценки тепловой и электромагнитной совместимости элементов: Fp = k1*S + k2*L + + k3*T + k4*J + k5*Q, где S – суммарная площадь перекрытия элементов; L – оценка длин межсоединений; T – показатель трассируемости; J – суммарное электромагнитное воздействие элементов друг на друга; Q – суммарное тепловое воздействие элементов друг на друга; k1, k2, k3, k4, k5 – коэффициенты, определяющие влияние каждой составляющей функции принадлежности на общую оценку.
Размер штрафа за перекрытие площадей размещаемых элементов зависит от суммарной площади пересечения всех элементов. При этом учитывается минимально допустимое расстояние между элементами.
Площадь пересечения двух элементов вычисляется следующим образом:
x11 = max(min(x1, x2 + d), min(x3, x4 + d));
x12 = min(max(x1, x2 + d), max(x3, x4 + d));
y11 = max(min(y1, y2 + d), min(y3, y4 + d));
y12 = min(max(y1, y2 + d), max(y3, y4 + d));
ЕСЛИ ((x12 – x11 >= 0) И (y12 – y11 >= 0))
ТО Rij = (x12 – x11) * (y12 – y11) ИНАЧЕ Rij = 0,
где x1, y1 – координаты верхнего левого угла первого прямоугольника; x2, y2 – координаты нижнего правого угла первого прямоугольника; x3, y3 – координаты верхнего левого угла второго прямоугольника; x4, y4 – координаты нижнего правого угла второго прямоугольника; d – минимально допустимое расстояние между элементами.
Для оценки длин межсоединений целесообразно использовать полупериметр описывающего прямоугольника цепи (рис. 2).

При решении задачи трассировки показателем качества решения является доля (процент) непротрассированных соединений. Дополнительным критерием качества трассировки является суммарная площадь пересечения областей описывающих прямоугольников всех цепей (рис. 3).

Параллельный алгоритм биоинспирированного поиска. Для совместного решения задач размещения и трассировки используется параллельный многопопуляционный генетический алгоритм [15–19]. Он предполагает параллельное выполнение эволюционных процессов на нескольких популяциях. Для обмена особями используются островная и буферная модели параллельного генетического алгоритма.
В островной модели синхронизация асинхронных процессов осуществляется в точках миграции. Оператор миграции применяется для обмена особями между популяциями. Отбор особей для миграции выполняется из некоторого количества хромосом популяции, имеющих наилучшее значение ЦФ размещения. Отбор осуществляется на основе оценки количества непротрассированных соединений. Для каждого варианта размещения, описываемого хромосомой, выполняется трассировка с помощью волнового алгоритма. Затем некоторое количество хромосом с наилучшим значением данного показателя копируется из одной популяции в другую. При этом из популяций удаляется такое же количество хромосом с наихудшим значением показателя. На рисунке 4 представлена схема модели параллельного генетического алгоритма, выполняемого на двух популяциях. На практике количество популяций может быть значительно больше.

В буферной модели обмен особями между популяциями осуществляется через общий промежуточный буфер хромосом. Обмен выполняется в точках миграции. К популяции, достигшей точки миграции, применяется оператор миграции.
Для трассировки используется волновой алгоритм. Работа алгоритма включает в себя три этапа: инициализацию, распространение волны и восстановление пути. Во время инициализации строится образ множества ячеек печатной платы, каждой ячейке приписываются атрибуты проходимости/непроходимости, запоминаются стартовая и финишная ячейки.
Далее от стартовой ячейки порождается шаг в соседнюю ячейку, при этом проверяется, проходима ли она и не является ли ранее помеченной в пути ячейкой. Для классификации соседних ячеек используется окрестность фон Неймана. Соседними ячейками считаются 4 ячейки по вертикали и горизонтали. При выполнении условий проходи- мости и непринадлежности ее к ранее помеченным в пути ячейкам в атрибут ячейки записывается число, равное количеству шагов от стартовой ячейки, на первом шаге это будет 1. Каждая ячейка, помеченная числом шагов от стартовой ячейки, становится стартовой, и из нее порождаются очередные шаги в соседние ячейки. Очевидно, что при таком переборе будет найден путь от начальной ячейки к конечной либо очередной шаг из любой порожденной в пути ячейки будет невозможен. Структурная схема волнового алгоритма представлена на рисунке 5.

После выбора метода кодирования решений и задания критериев оценки качества получаемых решений построим биоинспирированный алгоритм поиска на основе модифицированных генетических операторов.
Для создания начальной популяции использу- ется метод «дробовика». Он подразумевает случай- ный выбор альтернатив из всей области решений данной задачи [6]. После подсчета значений ЦФ для выбора решений применяется оператор селекции на основе метода «рулетки». Также в алгоритме используются модифицированные одноточечный оператор кроссинговера и многоточечный оператор мутации.
Развитие гибридных подходов и систем, ос- нованных на интеграции различных научных направлений, дает основания полагать, что при организации параллельной структуры вычислений и построении схемы процесса эволюции весьма перспективным является использование принципов построения многоагентных систем [22, 23]. Методы и модели организации многоагентных систем и технологий в последнее время наиболее бурно развиваются. Активно прорабатываются вопросы, связанные с использованием интеллектуальных организаций агентов в различных отраслях науки и экономики, в том числе в проектировании, робототехнике, в военных целях.
Эволюционное моделирование и многоагентные методы тесно взаимосвязаны. С одной стороны, применение принципов эволюционного развития позволяет решать задачи адаптации многоагентных систем к изменениям внешней среды. С другой, эволюция может быть движущей силой в процессе развития МАС, являться механизмом для достижения поставленных целей и обеспечивать мотивацию.
Можно выделить некоторые параллели (соответствия) между базовыми понятиями эволюционного моделирования и теории многоагентных систем:
|
Эволюционное моделирование
|
Теория многоагентных систем
|
|
Ген
|
Свойство агента
|
|
Хромосома
|
Набор свойств
|
|
Особь (решение)
|
Агент
|
|
Семья (2 родителя и 1 потомок)
|
Коллектив агентов
|
|
Популяция
|
Эволюционирующая многоагентная система
|
Также можно предположить, что принципы организации многоагентных систем могут быть успешно использованы для решения задачи распараллеливания вычислений.
Модуль нечеткого управления. Для повышения качества решений, получаемых биоинспирированным алгоритмом, в схему поиска включается нечеткий логический контроллер, регулирующий значения параметров основных эволюционных операторов. Таким образом, мы можем оценить текущее состояние процесса поиска и обеспечить возможность обратного управляющего воздействия на параметры генетического алгоритма с целью их оперативной коррекции [9, 11, 12, 24].
Для оценки текущего состояния популяции могут использоваться следующие величины [13, 14].
1. Разнообразие генотипа популяции. Определяется по формуле VG =  , где
, где  dmax, dmin – среднее, максимальное и минимальное расстояния хромосом популяции от лучшей. Очевидно, что VG Î [0, 1].
dmax, dmin – среднее, максимальное и минимальное расстояния хромосом популяции от лучшей. Очевидно, что VG Î [0, 1].
2. Фенотип особи. Зависит от значения ее функции пригодности VF Î [0,1]. Разнообразие фенотипа определяется по одной из следующих формул: VF = abs(fbest – ) / fbest; VF =
) / fbest; VF =  , где fbest,
, где fbest,  – лучшее и среднее значения функции пригодности.
– лучшее и среднее значения функции пригодности.
3. Скорость роста среднего значения функции пригодности по популяции SA Î [0, 1]. Она позволяет судить о том, насколько быстро происходит развитие особей в популяции. Вычисляется по следующей формуле: SA = (fave – favep) / fave, где fave, favep – среднее значение функции пригодности на текущей и предыдущей популяциях [14].
4. Изменение значения лучшей хромосомы в ходе эволюции:  , где
, где  ,
,  – лучшее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений.
– лучшее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений.
5. Среднее изменение значения функции пригодности популяции в ходе эволюции: 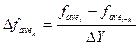 , где
, где  ,
,  – среднее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений.
– среднее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений.
Были выбраны следующие параметры для оценки эффективности эволюции:
 ;
;
 ;
;
 ;
;
 ,
,
где t – временной шаг; fbest(t) – лучшее значение ЦФ на итерации t; fbest(t – 1) – лучшее значение ЦФ на итерации (t – 1); fworst(t) – худшее значение ЦФ на итерации t; fave(t) – среднее значение ЦФ на итерации t; fave(t – 1) – среднее значение ЦФ на итерации (t – 1) [13, 14, 25, 26].
Переменные e1, e2, e3, e4 заданы на следующих интервалах: e1 Î [0; 1]; e2 Î [0; 1]; e3 Î [–1; 1]; e4 Î [–1; 1].
Выходными параметрами являются вероят- ности выполнения кроссинговера, мутации и миграции соответственно – Pc(t), ∆Pm(t), ∆Ps(t): Pc(t) Î [0; 1]; Pm(t) Î [0; 1]; Ps(t) Î [0; 1].
Для расчета выходных значений используется блок нечеткого управления, представленный ранее. В качестве входных переменных ͞xi будем использовать параметры ei. Полученные значения ͞y будут эквивалентны параметрам ∆Pc, ∆Pm, Ps(t). Для вычисления каждого из данных параметров будет использоваться отдельный модуль нечеткого управления.
Рассмотрим реализацию блока нечеткого управления, представленную двумя функциями, которые задают значения вероятности кроссинговера и мутации:
void GA::Population::set_d_ver_mut(){
kf[0]=-0.5; kf[1]=0; kf[2]=0.5;
fp[0].x=-50; fp[0].y=30;
fp[1].x=25; fp[1].y=20;
float x=exp(-((e1-fp[0].x)/fp[0].y)*((e1-fp[0].x)/fp[0].y));
float y=exp(-((e2-fp[1].x)/fp[1].y)*((e2-fp[1].x)/fp[1].y));
float s01=x*y;
float s1=x*y*kf[0];
fp[2].x=0; fp[2].y=30;
fp[3].x=50; fp[3].y=20;
x=exp(-((e1-fp[2].x)/fp[2].y)*((e1-fp[2].x)/fp[2].y));
y=exp(-((e2-fp[3].x)/fp[3].y)*((e2-fp[3].x)/fp[3].y));
float s02=x*y;
float s2=x*y*kf[1];
fp[4].x=50; fp[4].y=30;
fp[5].x=75; fp[5].y=20;
x=exp(-((e1-fp[4].x)/fp[4].y)*((e1-fp[4].x)/fp[4].y));
y=exp(-((e2-fp[5].x)/fp[5].y)*((e2-fp[5].x)/fp[5].y));
float s03=x*y;
float s3=x*y*kf[2];
float s0=s01+s02+s03;
float s=s1+s2+s3;
float a=s/s0;
ver_mut=ver_mut+a*100;
}
void GA::Population::set_d_ver_cross(){
kf[3]=-0.3; kf[4]=0; kf[5]=0.6;
fp[6].x=-50; fp[6].y=30;
fp[7].x=25; fp[7].y=20;
float x=exp(-((e1-fp[6].x)/fp[6].y)*((e1-fp[6].x)/fp[6].y));
float y=exp(-((e2-fp[7].x)/fp[7].y)*((e2-fp[7].x)/fp[7].y));
float s01=x*y;
float s1=x*y*kf[3];
fp[8].x=0; fp[8].y=30;
fp[9].x=50; fp[9].y=20;
x=exp(-((e1-fp[8].x)/fp[8].y)*((e1-fp[8].x)/fp[8].y));
y=exp(-((e2-fp[9].x)/fp[9].y)*((e2-fp[9].x)/fp[9].y));
float s02=x*y;
float s2=x*y*kf[4];
fp[10].x=50; fp[10].y=30;
fp[11].x=75; fp[11].y=20;
x=exp(-((e1-fp[10].x)/fp[10].y)*((e1-fp[10].x)/fp[10].y));
y=exp(-((e2-fp[11].x)/fp[11].y)*((e2-fp[11].x)/fp[11].y));
float s03=x*y;
float s3=x*y*kf[5];
float s0=s01+s02+s03;
float s=s1+s2+s3;
float a=s/s0;
ver_cross=ver_cross+a*100;
}
Завершающий этап в процессе проектирования модуля нечеткого управления – это определение формы представления нечетких множеств Aik, 1, …, n; k = 1, …, N. Например, это может быть функция Гаусса  , где параметры
, где параметры  и σik имеют физическую интерпретацию:
и σik имеют физическую интерпретацию:  – центр, а σik – ширина гауссовской кривой.
– центр, а σik – ширина гауссовской кривой.
Как будет показано далее, эти параметры могут модифицироваться в процессе обучения, что позволяет изменять положение и структуру нечетких множеств [25–27]. После объединения всех элементов функция для модуля нечеткого управления приобретает окончательный вид:
 .
.
Каждый элемент этой формулы можно задать в форме функционального блока (сумма, произведение, функция Гаусса), что после соответствующего объединения позволяет создать многослойную нейронную сеть. В рассматриваемом случае нейронная сеть будет содержать четыре слоя. Каждый элемент первого слоя реализует функцию принадлежности нечеткого множества Aik, 1, …, n; k = 1, …, N. В этот слой поступают входные сигналы ͞xi, а на его выходе формируются значения функции принадлежности для этих сигналов. На выходе первого слоя формируются значения функции принадлежности нечетким множествам. Конфигурация связей второго слоя соответствует базе правил, а мультипликаторы – блоку вывода. Применение мультипликаторов в качестве узлов этого слоя обусловлено тем, что в нечетких операциях используется операция умножения. Количество элементов этого слоя равно количеству правил, хранимых в базе. Третий и четвертый слои реализуют функции блока дефаззификации [25–27].
Очевидно, что описанная структура представляет собой многослойную сеть, основанную на идее нечеткого вывода. В отличие от «чистых» нейронных сетей каждый слой в целом и отдельные составляющие его элементы, как и конфигурация связей, все параметры и веса, имеют физическую интерпретацию. Это свойство оказывается необычайно важным, поскольку знания не распределяются по сети, могут быть легко локализованы и при необходимости откорректированы экспертом-наблюдателем.
В работе блока нечеткого управления используются 6 функций принадлежности для множеств Ak и 2 функции для множеств Bk. При этом kf[i] эквивалентны параметрам yk и интерпретируются как центры функций принадлежности нечетких множеств Bk; fp[i]x и fp[i]y интерпретируются соответственно как центр и ширина функции Гаусса для оценки степени принадлежности входных данных ͞xi, к соответствующим нечетким множествам Aik и соответствуют параметрам xik и σik в модуле нечеткого управления; величина a соответствует выходному значению модуля управления ͞у. В процессе работы блока вычисляются 24 функции принадлежности для множеств Aik и 6 функций для множеств Bk.
Программная реализация гибридного алгоритма
Архитектура приложения. Приложение состоит из следующих модулей: алгоритмы размещения и трассировки, модуль нечеткого управления, синтаксический анализатор и графический интерфейс. Алгоритмы размещения и трассировки реализованы в виде обобщенных алгоритмов, которые могут обрабатывать различные входные данные. Алгоритм совместного решения задач размещения и трассировки реализован на основе обобщенного алгоритма размещения, для которого определен метод расчета целевой функции размещения. На вход алгоритма подаются данные о топологии печатной платы. Алгоритм трассировки является вспомогательным и используется для оценки получаемых вариантов размещения. Модуль нечеткого управления используется для динамической настройки генетического алгоритма. База правил модуля нечеткого управления считывается из файла. Синтаксический анализатор используется для считывания данных о топологии печатной платы из файла, а также для записи данных в файл. Разработанная архитектура позволяет дополнять систему новыми свойствами и моделями поведения.
Хранение данных. Для хранения данных о топологии печатной платы используется LEF/DEF-спецификация. LEF (Library Exchange Format) – это спецификация для представления физической структуры интегральной схемы в формате ASCII. Она включает правила оформления и абстрактную информации об элементах. LEF применяется в сочетании с DEF (Design Exchange Format)-спецификацией, которая используется для представления полного размещения элементов интегральной схемы [28, 29].
Далее приведен пример описания элемента печатной платы при помощи LEF-спецификации:
MACRO ms00f80
PROPERTY LEF58_EDGETYPE "
EDGETYPE LEFT 2 ;
EDGETYPE RIGHT 2 ;
" ;
CLASS CORE ;
ORIGIN 0 0 ;
SIZE 1.6 BY 2.0 ;
SYMMETRY X Y R90 ;
SITE core ;
PIN o DIRECTION OUTPUT ;
PORT
LAYER metal2 ;
RECT 0.05 0.500 0.15 1.500 ;
END
END o
PIN a DIRECTION INPUT ;
PORT
LAYER metal1 ;
RECT 1.05 0.500 1.15 1.500 ;
END
END a
END ms00f80
Приведем также пример описания размещения элементов на печатной плате, а также описания цепей при помощи DEF-спецификации:
COMPONENTS 6;
- g2278701 ms00f80
+ PLACED (20, 10);
- g2278702 ms00f80
+ PLACED (20, 40);
- g2278703 ms00f80
+ PLACED (20, 70);
- g2278704 ms00f80
+ PLACED (60, 10);
- g2278705 ms00f80
+ PLACED (60, 40);
- g2278706 ms00f80
+ PLACED (60, 70);
END COMPONENTS
NETS 2;
- ternarymux_ln49_unr9_z_9_ (g2278701 a) (g2278705 o) (g2278703 a);
- ternarymux_ln49_unr9_z_10_ (g2278704 o) (g2278702 a) (g2278706 o);
Реализация алгоритма. Алгоритм размещения реализован классом CPlacingAlgorithm (см. http:// www.swsys.ru/uploaded/image/2018-3/2018-3-dop/2. jpg). Для выполнения алгоритма вызывается метод execute, который принимает указатель на класс CBoard, используемый для хранения топологии печатной платы. Результатом работы алгоритма является обработанная топология печатной платы с заданными позициями элементов и протрассированными соединениями. Параметры алгоритма устанавливаются с помощью метода setParams, который принимает структуру SParams, содержащую такие поля, как количество хромосом, количество итераций, вероятности кроссинговера и мутации, а также частота миграции. Генетические опера- торы устанавливаются при помощи указателей на абстрактные базовые классы, определяющие интерфейс операторов. Каждый указатель может соответствовать конкретной реализации оператора. Родительские и дочерние популяции хранятся в динамической памяти. Доступ к ним осуществляется с помощью векторов указателей. Промежуточный буфер хромосом также хранится в динамической памяти.
Алгоритм трассировки реализован классом CRoutingAlgorithm (см. http://www.swsys.ru/uploaded/image/2018-3/2018-3-dop/3.jpg). Для выполнения алгоритма вызывается метод execute, он принимает указатель на объект класса CBoard, в котором хранится топология печатной платы с размещенными элементами. Результатом работы алгоритма является обработанная топология печатной платы с протрассированными соединениями.
Алгоритм трассировки каждой цепи определяется конкретной реализацией базового класса CRoutingOperator. На текущем этапе разработки приложения используется только волновой алгоритм, реализованный в классе CWaveRoutingOperator.
Графический интерфейс. Для реализации графического интерфейса использовался фреймворк Qt 5.6. Qt представляет собой кроссплатформенный инструментарий разработки прикладного ПО, широко используемый для создания графических интерфейсов [30, 31]. Он написан на C++ и предоставляет мощные расширения этого языка. Включает в себя все основные классы, которые могут потребоваться при разработке ПО, начиная от элементов графического интерфейса и заканчивая классами для работы с сетью, БД и XML. В целом Qt является полностью объектно-ориентированным, легко расширяемым и поддерживающим технику компонентного программирования.
Рассмотрим основные элементы графического интерфейса разработанного приложения. Окно приложения состоит из меню, панели инструментов, рабочего пространства и текстового поля для вывода различной вспомогательной информации. Меню состоит из пунктов File и Help (рис. 6). Пункт меню File содержит подпункты Import и Exit. В пункте Import можно перейти к загрузке файлов, содержащих LEF- и DEF-спецификацию. Пункт Help содержит подпункты About и AboutQt, по нажатии на которые открываются окно с информацией о приложении и окно с информацией об используемой версии библиотеки Qt соответственно.

Панель инструментов содержит кнопку для загрузки конфигурации печатной платы по умолчанию, кнопки для запуска алгоритмов размещения, трассировки и обучения, а также кнопку настроек.
В окне настроек (рис. 7) можно задать параметры размещения элементов на печатной плате, такие как минимальное расстояние между элементами и шаг сетки размещения. Также можно установить параметры алгоритма: количество хромосом, количество итераций, первоначальные зна- чения вероятностей кроссинговера и мутации, частоту и интенсивность миграции, количество потоков при вычислении целевых функций алгоритмов размещения и трассировки и количество потоков выполнения основного алгоритма.

В рабочей области приложения осуществляется отрисовка текущего состояния печатной платы (см. http://www.swsys.ru/uploaded/image/2018-3/2018-3-dop/4.jpg). Для отрисовки используется класс QGraphicsView. Для представления графических элементов используются классы, наследуемые от класса QGraphicsItem. Размещаемые элементы печатной платы представляются классом СGraphic- Component, соединения – классом CGraphic-Net, сетка размещения – классом CGraphicGrid. Все графические элементы добавляются на сцену. Сцена является объектом класса QGraphicsScene. Сцена отрисовывается с помощью объекта класса QGra- phicsView, которым можно манипулировать посредством матрицы преобразований. Реализована возможность масштабирования и вращения графи- ческого отображения печатной платы. При увеличении графического отображения можно изменять видимую область путем перетаскивания. Размещенные графические элементы также можно перетаскивать, тем самым корректируя полученное размещение [10].
Для отображения графиков используется расширение для фреймворка QT – QCustomPlot. Это виджет QT, который используется для построения графиков и визуализации данных. Он не имеет дополнительных зависимостей и хорошо документирован. Данная библиотека позволяет получать качественное визуальное отображение графиков и диаграмм, при этом обладает высокой производительностью, что позволяет использовать ее в системах реального времени [30, 31].
Результаты вычислительных экспериментов
Для анализа эффективности разрабатываемых алгоритмов используются графики изменения среднего и минимального значений целевой функции размещения. На каждой итерации рассчитываются средние значения целевой функции всех популяций, в которых запущен эволюционный процесс. Также используются графики среднего и минимального значений целевой функции трассировки, рассчитываемых в точках миграции.
Для анализа работы нечеткого логического регулятора (НЛР) используются графики изменения его входных и выходных параметров (см. http:// www.swsys.ru/uploaded/image/2018-3/2018-3-dop/5. jpg, http://www.swsys.ru/uploaded/image/2018-3/ 2018-3-dop/6.jpg, http://www.swsys.ru/uploaded/image/2018-3/2018-3-dop/7.jpg).
Эффективность работы регулятора можно повысить введением блока обучения на базе нейронной сети. Коэффициенты сети можно определять путем случайного или направленного поиска. В качестве инструмента направленного поиска можно использовать генетический алгоритм. В результате использования блока обучения были определены оптимальные параметры (см. http://www.swsys.ru/ uploaded/image/2018-3/2018-3-dop/8.jpg, http:// www.swsys.ru/uploaded/image/2018-3/2018-3-dop/9. jpg, http://www.swsys.ru/uploaded/image/2018-3/ 2018-3-dop/10.jpg и рис. 8).

По умолчанию заданы параметры НЛР, определяющие следующие функции принадлежности (рис. 8):
для e1 и e2:  ,
,
 ,
,  ;
;
для e3 и e4:  ,
,
 ,
,  .
.
Нечеткий лингвистический регулятор позволяет получить значение вероятностей кроссинговера и мутации на основе четырех входных переменных, которые характеризуют эволюционный процесс. При этом зависимость выходных значений от входных переменных определяется параметрами НЛР. Количество этих параметров зависит от количества входных переменных, функций принадлежности и параметров, которые определяют каждую функцию принадлежности.
Параметры НЛР, используемые при исследовании, были получены с помощью генетического алгоритма обучения. Обучение проводилось на основе статистической информации о зависимости параметров НЛР и эффективности алгоритма размещения. Эта информация собиралась в процессе обучения. После обучения НЛР показал достаточно высокую эффективность, при этом благодаря обучению были получены зависимости выхода от входа, которые практически невозможно задать на основе опыта эксперта. Были получены достаточно сложные зависимости, которые проблематично описать, оперируя лингвистическими переменными.
Проанализировав полученные данные, можно сделать вывод о том, что для получения наилучшего решения задач размещения и трассировки необходимо использовать четыре потока параллельного генетического алгоритма. Дальнейшее увеличение количества потоков негативно отражается на результате решения задач.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, грант № 17-37-50076.
Литература
1. Alpert Ch.J., Dinesh P., Mehta D.P., Sapatnekar S.S. Handbook of algorithms for physical design automation. CRC Press, NY, USA, 2009.
2. Cohoon J.P., Karro J., Lienig J. Evolutionary algorithms for the physical design of VLSI circuit. In: Advances in Evolutionary Computing: Theory and Applications. A. Ghosh, S. Tsutsui (Eds.). Springer Verlag, London, 2003, pp. 683–712.
3. Норенков И.П. Основы автоматизированного проектирования. М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. 434 с.
4. Shervani N. Algorithms for VLSI physical design automation. Kluwer Acad. Publ., Dordrecht, 1995. 538 p.
5. Гладков Л.А., Курейчик В.М., Курейчик В.В., Сороколетов П.В. Биоинспирированные методы в оптимизации. М.: Физматлит, 2009. 384 с.
6. Гладков Л.А., Курейчик В.В., Курейчик В.М. Генетические алгоритмы. М.: Физматлит, 2010. 368 с.
7. Гладков Л.А., Курейчик В.В., Курейчик В.М., Род- зин С.И. Основы теории эволюционных вычислений: монография. Ростов н/Д.: Изд-во ЮФУ, 2010. 222 с.
8. Гладков Л.А. О некоторых подходах к построению гибридных интеллектуальных систем для решения графовых задач // Новости искусственного интеллекта. 2000. № 3. С. 71–90.
9. Michael A., Takagi H. Dynamic control of genetic algorithms using fuzzy logic techniques. Proc. 5th Intern. Conf. on Genetic Algorithms. Morgan Kaufmann, 1993, pp. 76–83.
10. Im S.-M., Lee J-J. Adaptive crossover, mutation and selection using fuzzy system for genetic algorithms. Artificial Life and Robotics. 2008, vol. 13, no. 1, pp. 129–133.
11. Herrera F., Lozano M. Fuzzy adaptive genetic algorithms: design, taxonomy, and future directions. Soft Computing, 2003, vol. 7, pp. 545–562.
12. Herrera F., Lozano M. Adaptation of genetic algorithm parameters based on fuzzy logic controllers. In: Genetic algorithms and soft computing. F. Herrera, J.L. Verdegay (Eds.), Physica-Verlag, Heidelberg, 1996, pp. 95–124.
13. Ярушкина Н.Г. Основы теории нечетких и гибридных систем. М.: Финансы и статистика, 2004. 320 с.
14. Батыршин И.З., Недосекин А.О., Стецко А.А., Тара- сов В.Б. Нечеткие гибридные системы. Теория и практика; [под ред. Н.Г. Ярушкиной]. М.: Физматлит, 2007. 208 с.
15. King R.T.F.A., Radha B., Rughooputh H.C.S. A fuzzy logic controlled genetic algorithm for optimal electrical distribution network reconfiguration. Proc. 2004 IEEE Intern. Conf. on Networking, Sensing and Control, Taipei, Taiwan, 2004, pp. 577–582.
16. Rodriguez M.A., Escalante D.M., Peregrin A. Efficient distributed genetic algorithm for rule extraction. Applied Soft Computing, 2011, vol. 11, pp. 733–743.
17. Alba E., Tomassini M. Parallelism and evolutionary algorithms. IEEE T. Evolut. Comput., 2002, vol. 6, pp. 443–461.
18. Zhongyang X., Zhang Y., Zhang L., Niu S. A parallel classification algorithm based on hybrid genetic algorithm. Proc. 6th World Congress on Intelligent Control and Automation, Dalian, China, 2006, pp. 3237–3240.
19. Кныш Д.С., Курейчик В.М. Параллельные генетические алгоритмы: Проблемы, обзор и состояние // Изв. РАН. Теория и системы управления. 2010. № 4. C. 72–82.
20. Гладков Л.А. Интегрированный алгоритм решения задач размещения и трассировки на основе нечетких генетических методов // Изв. ЮФУ. Технич. науки. 2011. № 7. C. 22–30.
21. Гладков Л.А. Гибридный генетический алгоритм решения задачи размещения элементов СБИС с учетом трассируемости соединений // Вестн. Ростов. гос. ун-та путей сообщения. 2011. № 3. С. 58–66.
22. Тарасов В.Б. От многоагентных систем к интеллектуальным организациям: философия, психология, информатика. М.: Эдиториал УРСС, 2002.
23. Гладков Л.А. Решение задач поиска и оптимизации решений на основе нечетких генетических алгоритмов и многоагентных подходов // Изв. ТРТУ. 2006. № 8. С. 83–88.
24. Пегат А. Нечеткое моделирование и управление. М.: БИНОМ. Лаборатория знаний, 2009.
25. Gladkov L.A., Gladkova N.V., Leiba S.N. Manufacturing scheduling problem based on fuzzy genetic algorithm. Proc. IEEE East-West Design & Test Symposium (EWDTS’2014). Kiev, Ukraine, 2014, pp. 209–213.
26. Gladkov L.A., Gladkova N.V., Legebokov A.A. Organization of knowledge management based on hybrid intelligent methods. In: Software engineering in intelligent systems. Proc. 4th Comp. Sc. On-line Conf. 2015 (CSOC 2015), Springer, Switzerland, 2015, vol. 3, pp. 107–113.
27. Гладков Л.А., Гладкова Н.В., Лейба С.Н. Размещение элементов схем ЭВА на основе гибридных интеллектуальных методов // Изв. ЮФУ. Технич. науки. 2015. № 4. C. 25–36.
28. Гамма Э., Хелм Р., Джонсон Р., Влиссидес Д. Приемы объектно-ориентированного программирования. Паттерны проектирования. СПб: Питер, 2001. 368 с.
29. Макконел С. Совершенный код. СПб: Питер, 2005. 896 с.
30. Qt Documentation. URL: http://doc.qt.io/qt-5/reference-overview.html (дата обращения: 20.02.2018).
31. QCustomPlot. URL: http://qcustomplot.com/index.php/ introduction (дата обращения: 20.02.2018).
References
- Alpert Ch.J., Mehta D.P., Sapatnekar S.S. Handbook of Algorithms for Physical Design Automation. CRC Press, NY, USA, 2009.
- Cohoon J.P., Karro J., Lienig J. Evolutionary algorithms for the physical design of VLSI circuits. Advances in Evolutionary Computing: Theory and Applications. A. Ghosh, S. Tsutsui (Eds.) Springer Verlag Publ., London, 2003,
pp. 683–712.
- Norenkov I.P. Fundamentals of Computer Aided Design. Moscow, Bauman MSTU Publ., 2010, 434 p.
- Shervani N. Algorithms for VLSI Physical Design Automation. Kluwer Academy Publ., Dordrecht, 1995, 538 p.
- Gladkov L.A., Kureychik V.M., Kureychik V.V., Sorokoletov P.V. Bioinspirated Methods in Optimization. Moscow, Fizmatlit Publ., 2009, 384 p.
- Gladkov L.A., Kureychik V.V., Kureychik V.M. Genetic Algorithms. Moscow, Fizmatlit Publ., 2010, 368 p.
- Gladkov L.A., Kureychik V.V., Kureychik V.M., Rodzin S.I. Fundamentals of the Theory of Evolutionary Computations. Monograph. Rostov-on-Don, SFedU Publ., 2010, 222 p.
- Gladkov L.A. On some approaches to constructing hybrid intelligent systems for solving graph tasks. News of Artificial Intelligence. 2000, no. 3, pp. 71–90 (in Russ.).
- Michael A., Takagi H. Dynamic control of genetic algorithms using fuzzy logic techniques. Proc. 5th Intern. Conf. on Genetic Algorithms. Morgan Kaufmann Publ., 1993, pp. 76–83.
- Im S.-M., Lee J-J. Adaptive crossover, mutation and selection using fuzzy system for genetic algorithms. Artificial Life and Robotics. 2008, vol. 13, no. 1, pp. 129–133.
- Herrera F., Lozano M. Fuzzy Adaptive Genetic Algorithms: design, taxonomy, and future directions. Soft Computing. 2003, vol. 7, pp. 545–562.
- Herrera F., Lozano M. Adaptation of genetic algorithm parameters based on fuzzy logic controllers. Genetic Algorithms and Soft Computing. F. Herrera, J.L. Verdegay (Eds.). Physica-Verlag, Heidelberg Publ., 1996, pp. 95–124.
- Yarushkina N.G. Fundamentals of the Theory of Fuzzy and Hybrid Systems. Moscow, Finansy i statistika Publ., 2004, 320 p.
- Batyrshin I.Z., Nedosekin A.O., Stetsko A.A., Tarassov V.B. Fuzzy Hybrid Systems. Theory and Practice. N.G. Yarushkina (Ed.). Moscow, Fizmatlit Publ., 2007, 208 p.
- King R.T.F.A., Radha B., Rughooputh H.C.S. A fuzzy logic controlled genetic algorithm for optimal electrical distribution network reconfiguration. Proc. 2004 IEEE Intern. Conf. on Networking, Sensing and Control. Taipei, Taiwan. 2004, pp. 577–582.
- Rodriguez M.A., Escalante D.M., Peregrin A. Efficient distributed genetic algorithm for rule extraction. Applied Soft Computing. 2011, vol. 11, pp. 733–743.
- Alba E., Tomassini M. Parallelism and evolutionary algorithms. IEEE T. Evolut. Comput. 2002, vol. 6. pp. 443–461.
- Zhongyang X., Zhang Y., Zhang L., Niu S. A parallel classification algorithm based on hybrid genetic algorithm. Proc. 6th World Congr. on Intelligent Control and Automation. Dalian, China. 2006, pp. 3237–3240.
- Knysh D.S., Kureychik V.M. Parallel genetic algorithms: a survey and problem state of the art. J. of Computer and Systems Sciences Intern. 2010, vol. 49, iss. 4, pp. 579–589 (in Russ.).
- Gladkov L.A. Integrated algorithm for solving allocation and tracing problems based on fuzzy genetic methods. Izvestiya SFedU. Engineering Sciences. Taganrog, 2011, no. 7, pp. 22–30 (in Russ.).
- Gladkov L.A. Hybrid genetic algorithm for solving the problem of VLSI elements placement taking into account the traceability of connections. Vestnik RGUPS. Rostov-on-Don, 2011, no. 3, 2011, pp. 58–66 (in Russ.).
- Tarasov V.B. From Multi-Agent Systems to Intellectual Organizations: Philosophy, Psychology, Informatics. Moscow, Editorial URSS Publ., 2002.
- Gladkov L.A. Solving the problems of search and optimization of solutions based on fuzzy genetic algorithms and multi-agent approaches. Proc. of TRTU. Thematic Issue: Intelligent CAD. Taganrog, 2006, no. 8, pp. 83–88 (in Russ.).
- Pegat A. Fuzzy Modeling and Control. Moscow, BINOM. Laboratoriya znany Publ., 2009.
- Gladkov L.A., Gladkova N.V., Leiba S.N. Manufacturing scheduling problem based on fuzzy genetic algorithm. Proc. IEEE East-West Design & Test Symp. (EWDTS’2014). Kiev, Ukraine, 2014, pp. 209–213.
- Gladkov L.A., Gladkova N.V., Legebokov A.A. Organization of knowledge management based on hybrid intelligent methods. Software engineering in intelligent systems. Proc. 4th Computer Science On-line Conf. 2015 (CSOC 2015). Vol. 3: Software Engineering in Intelligent Systems. Springer Intern. Publ., Switzerland, 2015, pp. 107–113.
- Gladkov L.A. Gladkova N.V., Leyba S.N. Placement of elements of EVA schemes based on hybrid intellectual methods. Izvestiya SFedU. Engineering Sciences. Thematic Issue: Intelligent CAD. Taganrog, 2015, no. 4, pp. 25–36 (in Russ.).
- Gamma E., Helm R., Johnson R., Vlissides J. Design Patterns. Elements of Reusable Object-Oriented Software. Addison-Wesley Publ., 1994, 395 p. (Russ. ed.: St. Petersburg, Piter Publ., 2001).
- McConnell S. Code Complete. Microsoft Press, 1993, 857 p. (Russ. ed.: St. Petersburg, Piter Publ., 2005).
- Qt Documentation. Available at: http://doc.qt.io/qt-5/reference-overview.html (accessed February 20, 2018).
- QCustomPlot. Available at: http://qcustomplot.com/index.php/introduction (accessed February 20, 2018).








 , где
, где  dmax, dmin – среднее, максимальное и минимальное расстояния хромосом популяции от лучшей. Очевидно, что VG Î [0, 1].
dmax, dmin – среднее, максимальное и минимальное расстояния хромосом популяции от лучшей. Очевидно, что VG Î [0, 1]. ) / fbest; VF =
) / fbest; VF =  , где fbest,
, где fbest,  , где
, где  ,
,  – лучшее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений.
– лучшее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений.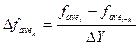 , где
, где  ,
,  – среднее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений.
– среднее значение функции пригодности на i-м и (i–k)-м поколениях; DY – точность нахождения решения; k – количество анализируемых поколений. ;
; ;
; ;
; ,
, , где параметры
, где параметры  и σik имеют физическую интерпретацию:
и σik имеют физическую интерпретацию:  .
.


 ,
, ,
,  ;
; ,
, ,
,  .
.