Развитие и внедрение информационных технологий вызвало резкое увеличение количества запросов на принятие, обработку и вывод данных в высоконагруженных системах [1–4], использование которых требует качественного увеличения производительности в вычислительных системах на каждое ядро [5]. Высоконагруженные системы чаще всего преобразуются в кластеры для повышения отказоустойчивости [6]. Под кластером понимается объединение физических серверов в единый аппаратный ресурс. Кластеры используются для решения высокопроизводительных задач в медицине, при выполнении государственных заказов нефтегазовой и энергетической отраслей, а также применяются везде, где используется численное (компьютерное) моделирование [7]. Зачастую возникает проблема перегрузки центрального процессора при нестабильном распределении вычислительных процессов по всем ядрам кластера. Это приводит к дестабилизации рабочей среды каждой ЭВМ.
Вопросами распределенных вычислений занимаются многие исследователи, о чем свидетельствуют многочисленные публикации. Например, Штейнберг О.Б. рассматривал преобразование программ, выполняющее круговой сдвиг операторов тела цикла, с последующим использованием для распараллеливания [8]. Посыпкин М.А. и Тант Син Си Ту исследовали параллельные варианты метода динамического программирования для задачи о сумме подмножеств [9]. Овчаренко О.И. получил оценки эффективности и ускорения на примере решения систем алгебраических уравнений методом циклической редукции на HPC-кластере [10]. Пе- липец А.В. распараллеливал решения задач линейной алгебры с последующим достижением минимизации числа используемых внешних кана- лов [11].
Для решения проблемы распределенных вычислений нередко используются и аппаратные технологии: ставятся дополнительные физические серверы с последующим добавлением в кластер. Но данное решение затратно и не всегда приемлемо.
Разрабатываемый аппаратно-программный модуль позволяет распределять вычислительные процессы по всем физическим и логическим яд- рам кластера (в том числе и при атаках DoS и DDoS), способствуя равномерному распределению нагрузки, с последующим повышением производительности в UNIX-подобных системах. Выбор UNIX-подобных систем объясняется тем, что они более универсальны и лучше подходят для решения ресурсоемких задач. К тому же они более производительные. Например, устанавливать Windows на вычислительный кластер не всегда рационально, так как зачастую важна производительность. К тому же существуют версии ОС Linux, в которых отсутствует графический интерфейс, что позволяет дополнительно экономить ресурсы ЭВМ.
Целью авторов данной работы является разработка программного модуля для распределения вычислительных процессов, что позволяет снизить загруженность физических и логических ядер сервера.
Обзор существующих решений
 Если рассматривать ОС семейств Windows и UNIX, то необходимо выделить функцию распределения нагрузки по физическим и логическим ядрам как персонального компьютера, так и сервера. Например, функция распределения загруженности центрального процессора в ОС семейства Windows. Схема работы данного распределения представлена на рисунке 1. Соответственно, управляющим элементом на программном уровне является ОС, взаимодействующая с аппаратными ресурсами, в том числе и с центральным процессором. При загруженности ядра на 50–60 % (данные значения характерны для Intel Xeon 5670, у других процес- соров нагрузка может варьироваться в другом диапазоне) происходит распределение нагрузки по другим ядрам. Но у данной функции имеется существенный недостаток: нестабильная работоспособность, то есть загруженность каждого ядра может достигать 100 % при запуске ресурсоемкого приложения. Соответственно, если приложение однопоточное, ОС Windows не сможет перенести его на другое ядро, так как не обладает функционалом переноса именно процессов, и приложению не будет хватать производительности для полноценного функционирования. Таким образом, ОС Windows может распределять нагрузку только многопоточных (имеющих возможность работы на нескольких ядрах одновременно) приложений.
Если рассматривать ОС семейств Windows и UNIX, то необходимо выделить функцию распределения нагрузки по физическим и логическим ядрам как персонального компьютера, так и сервера. Например, функция распределения загруженности центрального процессора в ОС семейства Windows. Схема работы данного распределения представлена на рисунке 1. Соответственно, управляющим элементом на программном уровне является ОС, взаимодействующая с аппаратными ресурсами, в том числе и с центральным процессором. При загруженности ядра на 50–60 % (данные значения характерны для Intel Xeon 5670, у других процес- соров нагрузка может варьироваться в другом диапазоне) происходит распределение нагрузки по другим ядрам. Но у данной функции имеется существенный недостаток: нестабильная работоспособность, то есть загруженность каждого ядра может достигать 100 % при запуске ресурсоемкого приложения. Соответственно, если приложение однопоточное, ОС Windows не сможет перенести его на другое ядро, так как не обладает функционалом переноса именно процессов, и приложению не будет хватать производительности для полноценного функционирования. Таким образом, ОС Windows может распределять нагрузку только многопоточных (имеющих возможность работы на нескольких ядрах одновременно) приложений.
 При рассмотрении ОС семейства UNIX необходимо учесть, что они более производительны и стабильны. В качестве тестовой ОС использовалась Ubuntu 17.10. В данной системе модуль распределения загруженности системы работает так, как показано на рисунке 2.
При рассмотрении ОС семейства UNIX необходимо учесть, что они более производительны и стабильны. В качестве тестовой ОС использовалась Ubuntu 17.10. В данной системе модуль распределения загруженности системы работает так, как показано на рисунке 2.
Соответственно, ОС взаимодействует с ресурсами центрального процессора для полного ис- пользования его мощностей. Также программное ядро является неотъемлемой частью любой ОС, в частности Ubuntu 17.10. В рассматриваемом случае процессор нагружался различными вычислительными процессами. При большой загруженности ядра одним процессом (когда приложение является многопоточным и умеет работать с несколькими ядрами одновременно) происходит распределение нагрузки между другими ядрами. Существенным недостатком является неавтоматизированная настройка прерываний по физическим и логическим ядрам сервера. Например, в случае DDoS-атаки на определенный порт, под которым работает приложение, произойдет повышение нагрузки самим процессом и сетевым стеком. Таким образом, в UNIX-подобных системах нагрузка по ядрам распределяется только в случае возможности работы процесса в режиме многопоточности. Сравнение с предлагаемым решением дано далее.
Описание графов внутренних состояний и матрицы переходов
 Графы внутренних состояний разрабатываемого алгоритма (аппаратно-программного модуля) изображены на рисунке 3.
Графы внутренних состояний разрабатываемого алгоритма (аппаратно-программного модуля) изображены на рисунке 3.
Каждый равновесный граф (рис. 1) представляет собой равновероятный переход системы из одного состояния в другое за одинаковый промежуток времени. В графах используется реализация случайных событий: после нескольких этапов (j) разработанная система (аппаратно-программный модуль) переходит в состояние «1». Таким образом, вводится вектор вероятности состояния перехода:
p(j) = (p1(j), p2(j), …, pn(j))T. (1)
Также добавляется вектор начальных состояний. Это необходимо для реализации возможности перехода из начальных состояний по всей системе:
p(0) = (p1(0), p2(0), …, pn(0))T. (2)
Далее реализуется матрица вероятностей переходов, где
I º (1, 1, …, 1) Î Mln(R). (3)
Таким образом,
 (4)
(4)
где j ³ 0, можно представить в виде Ip(j) = 1, j ³ 0. Это позволит системе находиться в одном из принимаемых состояний. Разработанный аппаратно-программный модуль (из математической модели, рис. 1) принимает следующие состояния:
PRK – состояние проверки общей загруженности кластера;
RSP – состояние распределения вычислительных процессов по физическим и логическим ядрам всего кластера;
PRK1 – состояние повторной проверки загруженности кластера (после распределения вычислительных процессов по физическим и логическим ядрам всего кластера);
KSR – состояние подсчета количества физических серверов, а также физических и логических ядер в кластере;
PRST – состояние проверки сетевого стека: нагрузка на центральный процессор, составленные лимиты в конфигурационных файлах;
RSSN – состояние распределения сетевой нагрузки по физическим и логическим ядрам всего кластера.
Значение 0,05 (рис. 1) показывает время перехода от одного состояния к другому, а также соответствует количеству задействованных дуг. Матрица вероятности строится на основе перехода от состояния к состоянию, суммируя общий проделанный путь.
Таким образом, матрица вероятности переходов
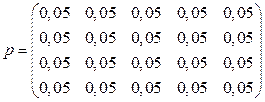 , (5)
, (5)
где 0 £ p £ 1 и значение перехода не может быть 0.
Таким образом,  (6)
(6)
Это дает возможность переходов по системе алгоритма за один шаг, позволяя выполнять операции с более высокой скоростью. В результате повышается реагирование алгоритма на повышенную загруженность физических и логических ядер, что ускоряет перенос вычислительных процессов по физическим серверам кластера.
Доработка цепей Маркова в модуле Distribution
Новизна работы заключается в равномерном распределении вычислительных процессов по физическим и логическим ядрам кластера за счет доработки цепей Маркова. Для реализации вводятся распределенные состояния цепей Маркова (P1). Под состоянием подразумевается упорядоченная пара чисел в системе массового обслуживания (СМО): (n, m) = s, (7)
где n – номер сервера кластера; m – количество занятых мест в очереди на обработку; s – распределенное состояние цепи Маркова. Таким образом, распределение цепи, за счет которого и будет производиться распределение вычислительных процессов по физическим и логическим ядрам кластера, рассчитывается по следующей формуле:
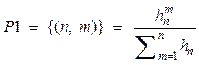 , (8)
, (8)
где n – порядковый номер сервера в кластере; m – места на обработку в очереди (под местами на обработку понимается свободное количество заявок);  – интенсивная обработка заявок (сетевых пакетов/вычислительных процессов), где m – количество сетевых пакетов, n – количество вычислительных процессов. Измерение обработки происходит многопоточно (шт./с). Это позволяет добиться более высокого процента успешных обработок заявок по переносу вычислительных процессов по кластеру. Далее необходимо узнать вероятность занятых мест в очереди на пернос процессов:
– интенсивная обработка заявок (сетевых пакетов/вычислительных процессов), где m – количество сетевых пакетов, n – количество вычислительных процессов. Измерение обработки происходит многопоточно (шт./с). Это позволяет добиться более высокого процента успешных обработок заявок по переносу вычислительных процессов по кластеру. Далее необходимо узнать вероятность занятых мест в очереди на пернос процессов:
 , (9)
, (9)
где Nn – количество заявок на одно ядро (как физическое, так и логическое). Это позволяет узнать вероятность занятых мест в очереди на обработку, но не реализует распределение очереди. Таким образом, за счет формулы (8) обрабатываются заявки по переносу вычислительных процессов. Соответственно, при применении формулы (9) возможно узнать только вероятность занятых мест в очереди на перенос процессов. Формула (9) была дорабо- тана из уравнения  (получена при стохастическом моделировании различных процессов СМО) [12], где R0 – количество заявок на обработку; P0 – состояние системы; P – вероятность перехода; K0 – лимит на количество заявок; L0 – количество заявок в обработке. Схема работы переноса вычислительных процессов (с применением цепей Маркова) по кластеру показана на рисунке 4.
(получена при стохастическом моделировании различных процессов СМО) [12], где R0 – количество заявок на обработку; P0 – состояние системы; P – вероятность перехода; K0 – лимит на количество заявок; L0 – количество заявок в обработке. Схема работы переноса вычислительных процессов (с применением цепей Маркова) по кластеру показана на рисунке 4.
Повышенная производительность достигается за счет равномерного распределения нагрузки по физическим и логическим ядрам кластера программным модулем на основе цепей Маркова.
Также при применении цепей Маркова для задачи равномерного распределения нагрузки существует ограничение по количеству заявок СМО. Соответственно, если n + m ³ 20 000 000 (m – количество сетевых пакетов; n – количество вычислительных процессов), то изначально Distribution (при помощи цепей Маркова) будет равномерно распределять нагрузку на тех серверах, куда больше всего поступает заявок.
Таким образом, при помощи доработанных цепей Маркова повышается производительность физического сервера и вычислительного кластера путем снижения нагрузки на ресурсы ЭВМ.
Разработка и реализация аппаратно-программного модуля Distribution
 Разрабатываемый аппаратно-программный модуль Distribution (переводной вариант «Распределение») предназначен для равномерного распреде- ления нагрузки на вычислительные ресурсы по физическим серверам кластера. Принцип работы модуля Distribution представлен на рисунке 5.
Разрабатываемый аппаратно-программный модуль Distribution (переводной вариант «Распределение») предназначен для равномерного распреде- ления нагрузки на вычислительные ресурсы по физическим серверам кластера. Принцип работы модуля Distribution представлен на рисунке 5.
Реализованные команды модуля Distribution, выполняемые с помощью удаленного клиента и консольной оболочки, без потребления ресурсов в деактивированном состоянии показаны в таблице 1.

Реализованные команды организуют распределение вычислительных процессов при нагрузке сетевого стека на центральный процессор с дополнительными настройками из веб-части.
Апробация Distribution
Апробация Distribution проводилась в несколько этапов. Первый этап представляет собой анализ загруженности физических ресурсов разработанными функциями аппаратно-программного модуля. Это позволяет узнать нагрузку на ЭВМ в теории и практике. Вторая часть тестирования заключается в выявлении потребления физических ресурсов сетевым стеком при массивных атаках типа DoS и DDoS и без обработки модулем Distribution. Данный фрагмент апробации предоставляет возможность получения результатов нагрузки без распределения нагрузки по физическим и логическим ядрам ЭВМ. Третий этап апробации представляет собой нагрузку, которая получена в результате DoS- и DDoS-атак, с последующей обработкой модулем Distribution. На данном этапе была выявлена разница в нагрузке до и после обработки модулем Distribution, а также получена средняя нагрузка на ресурсы ЭВМ. Это позволяет проанализировать прирост производительности за счет равномерного распределения нагрузки (сетевой и вычислительных процессов) по физическим и логическим ядрам кластера.
Тестирование аппаратно-программного модуля Distribution проводилось в течение одного календарного месяца на кластере со следующими характеристиками:
- количество физических серверов – 30;
- процессор Intel Xeon 5670 (CPU – 60, физических ядер – 360, количество потоков – 720);
- оперативная память – 960 GB;
- твердотельные накопители – RAID 10 (Intel S3710 SSDSC2BA012T401 800 GB каждый);
- 2xCisco WS-C4948-10GE;
- внешний сетевой канал – 20 Гбит/с.
Необходимо отметить, что под физическими и логическими ядрами понимается применение технологии Hyper-threading. На некоторых серверах кластера включена данная технология. Соответственно, одно физическое ядро определяется как два логических.
Апробация проводилась для получения результатов нагрузки сетевого стека на кластер до и после активации модуля Distribution с последующим выявлением его эффективности и производительности. Для более тщательного тестирования осуществлялось увеличение атаки как в размерах (GB/s), так и в емкости (количество входящих пакетов в секунду). Это позволило выявить устойчивость к высоким сетевым и вычислительным нагрузкам.
Промежуточные результаты (суточный замер) потребляемых ресурсов при активном состоянии модуля с последующей атакой в 1 GB/s представлены таблице 2.
Таблица 2
Анализ загруженности вычислительных ресурсов (%) при запуске разработанных команд в модуле Distribution
Table 2
Analysis of computing resources workload (%) at the start of the developed commands in the Distribution module
|
Команда
|
Потребление CPU
|
Потребление ОЗУ
|
Нагрузка на винчестер
|
|
Старт
|
0,50
|
0,04
|
0,01
|
|
Стоп
|
0,00
|
0,00
|
0,00
|
|
Перезапуск
|
0,50
|
0,03
|
0,01
|
|
Проверка нагрузки сетевого стека
|
0,70
|
0,05
|
0,01
|
|
Установка значения загруженности ядра
|
0,00
|
0,00
|
0,00
|
Суммарная мощность потребления центрального процессора (CPU) приравнивается к 1,7 %, ОЗУ – 0,12 %, винчестер – 0,03 %.
В ходе тестирования потребления ресурсов при DoS- и DDoS-атаках были получены результаты, которые представлены в таблицах 3 и 4.
Таблица 3
Результаты тестирования потребления физических ресурсов сетевым стеком без обработки модулем Distribution в течение десяти дней
Table 3
Test results of physical resource consumption by a network stack without processing by the Distribution module during ten days
|
A
|
B
|
C
|
D
|
A
|
B
|
C
|
D
|
|
1
|
0,50
|
15000
|
10,00
|
6
|
1,50
|
65000
|
18,90
|
|
2
|
0,70
|
25000
|
12,00
|
7
|
1,90
|
75000
|
19,90
|
|
3
|
0,90
|
35000
|
14,00
|
8
|
2,40
|
85000
|
21,80
|
|
4
|
1,10
|
45000
|
16,00
|
9
|
2,60
|
95000
|
22,24
|
|
5
|
1,30
|
55000
|
17,50
|
10
|
2,80
|
100000
|
23,12
|
В таблице 3 приняты следующие обозначения: A – день; B – суммарная мощность атаки, GB/s; C – количество сетевых пакетов в секунду; D – средняя нагрузка на CPU, %.
Средняя нагрузка на центральный процессор – 17,54 %, ОЗУ – 0 %, SSD – 0 %.
Таблица 4
Результаты тестирования загруженности физических ресурсов сетевым стеком при обработке модулем Distribution в течение десяти дней
Table 4
Test results of physical resource load of by a network stack without processing by the Distribution module during ten days
|
День
|
Суммарная мощность атаки, GB/s
|
Количество сетевых пакетов в секунду
|
Средняя нагрузка на CPU, %
|
Среднее потребление ОЗУ, %
|
Средняя нагрузка на SSD, %
|
|
1
|
0,50
|
15 000
|
0,20
|
0,01
|
0,010
|
|
2
|
0,70
|
25 000
|
0,30
|
0,02
|
0,020
|
|
3
|
0,90
|
35 000
|
0,50
|
0,03
|
0,025
|
|
4
|
1,10
|
45 000
|
0,70
|
0,04
|
0,034
|
|
5
|
1,30
|
55 000
|
1,00
|
0,05
|
0,050
|
|
6
|
1,50
|
65 000
|
1,25
|
0,06
|
0,070
|
|
7
|
1,90
|
75 000
|
1,55
|
0,07
|
0,100
|
|
8
|
2,00
|
85 000
|
1,78
|
0,08
|
0,110
|
|
9
|
2,60
|
95 000
|
2,00
|
0,09
|
0,120
|
|
10
|
2,80
|
100 000
|
2,35
|
0,10
|
0,130
|
Средняя нагрузка на центральный процессор – 1,16 %, ОЗУ – 0,055 %, SSD – 0,066 %.
Различия в нагрузке на физические ресурсы в суточном эквиваленте показаны в таблице 5.
Таблица 5
Сравнение результатов, полученных при тестировании нагрузки на CPU с обработкой и без обработки программным модулем Distribution
Table 5
Comparison of the results obtained when testing the CPU load with and without processing by the Distribution module
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
|
1
|
10,00
|
0,20
|
50,00
|
0,01
|
0,01
|
0,01
|
0,01
|
|
2
|
12,00
|
0,30
|
40,00
|
0,02
|
0,02
|
0,02
|
0,02
|
|
3
|
14,00
|
0,50
|
28,00
|
0,03
|
0,03
|
0,025
|
0,02
|
|
4
|
16,00
|
0,70
|
22,80
|
0,04
|
0,04
|
0,034
|
0,03
|
|
5
|
17,50
|
1,00
|
17,50
|
0,05
|
0,05
|
0,05
|
0,05
|
|
6
|
18,90
|
1,25
|
15,12
|
0,06
|
0,06
|
0,07
|
0,07
|
|
7
|
19,90
|
1,55
|
12,83
|
0,07
|
0,07
|
0,10
|
0,10
|
|
8
|
21,80
|
1,78
|
12,24
|
0,08
|
0,08
|
0,11
|
0,11
|
|
9
|
22,24
|
2,00
|
11,12
|
0,09
|
0,09
|
0,12
|
0,12
|
|
10
|
23,12
|
2,35
|
9,83
|
0,10
|
0,10
|
0,13
|
0,13
|
В таблице 5 приняты следующие обозначения: A – день; B – средняя нагрузка на CPU (до обработки), %; C – средняя нагрузка на CPU (после обработки), %; D – разница в нагрузке на CPU, единиц; E – среднее потребление ОЗУ (после обра- ботки), %; F – разница в потреблении ОЗУ, единиц; G – средняя нагрузка на SSD (после обработки), %; H – разница в нагрузке на SSD, единиц.
Средняя разница в нагрузке на центральный процессор понижается на 11,15 единицы, потребление оперативной памяти повышается на 0,155 единицы, загруженность твердотельного накопителя (SSD) увеличилась на 0,691 единицы. Нагрузка на SSD возникала за счет логирования (записи) данных о равномерном распределении, а также при записи и анализе в автоматизированном режиме сетевых пакетов. Таким образом, вышеприведенные показатели подтверждают эффективность работоспособности разработанного модуля Distribution.
Сравнение с аналогичными решениями
Для выявления эффективности разработанного аппаратно-программного модуля приведем сравнение с аналогичными решениями, представленными выше (табл. 6).
Таблица 6
Сравнение результатов с аналогами
Table 6
Comparison of the results with analogues
|
A
|
B
|
C
|
D
|
E
|
F
|
|
1
|
15,00
|
13,00
|
7,00
|
2,14
|
1,85
|
|
2
|
17,00
|
14,00
|
8,00
|
2,12
|
1,75
|
|
3
|
18,00
|
15,00
|
9,00
|
2,00
|
1,66
|
|
4
|
20,00
|
19,00
|
10,00
|
2,00
|
1,90
|
|
5
|
23,00
|
25,00
|
11,00
|
2,09
|
2,27
|
|
6
|
24,00
|
27,00
|
12,00
|
2,00
|
2,25
|
|
7
|
26,00
|
31,00
|
13,00
|
2,00
|
2,38
|
|
8
|
29,00
|
32,00
|
14,00
|
2,07
|
2,28
|
|
9
|
35,00
|
33,00
|
15,00
|
2,33
|
2,20
|
|
10
|
40,00
|
34,00
|
16,00
|
2,50
|
2,12
|
Примечание. Приняты следующие обозначения: A – день; B – нагрузка в Windows, %; C – нагрузка в Ubuntu 17.10 без модуля, %; D – нагрузка с использованием предлагаемого решения, %; E – разница в нагрузке на CPU между предлагаемым решением и Windows, единиц; F – разница в нагрузке на CPU между предлагаемым решением и Linux, раз.
Разница (R) вычислялась по следующей формуле:
 , (11)
, (11)
где L – первый показатель нагрузки (например B); P – второй показатель нагрузки (D).
Таким образом, разработанное программное решение существенно снижает загруженность (в два и более раз) физического сервера методом распределения нагрузки ЭВМ по ядрам, повышает производительность, что дает возможность более рацио- нального использования ресурсов физического сервера в различных целях.
Заключение
В ходе проведенных исследований и разработок был реализован аппаратно-программный модуль Distribution, предназначенный для равномерного распределения нагрузки по физическим серверам кластера, со следующими функциональными возможностями:
а) проверка загруженности физических и логических ядер на сервере;
б) создание условий проверки нагрузки сетевым стеком на центральный процессор;
в) удаленное управление программным модулем через веб-интерфейс;
г) сохранение полученных данных в СУБД MySQL;
д) проверка процентного соотношения загруженности каждого ядра;
е) вывод данных в веб-интерфейс;
ж) включение и отключение модуля при необходимости;
з) распределение нагрузки по всем серверам кластера.
Функции «a», «б», «д» и «з» разработаны за счет доработки цепей Маркова. Это способствует повышению производительности каждого физического сервера всего кластера с последующим увеличением сетевой пропускной способности (по входящим/исходящим сетевым пакетам).
Представленная математическая модель разработанного аппаратно-программного модуля Distribution показывает возможность переходов между состояниями выполнения функций при активированном аппаратно-программном модуле. Показана научная новизна, заключающаяся в доработке цепей Маркова для распределения и переноса вычислительных процессов по физическим и логическим ядрам кластера.
В работе обоснована целесообразность применения модуля Distribution на вычислительных ресурсах различной мощности. Предложена методика распределения нагрузки на физические ресурсы по серверам кластера.
Кроме того, проведено множество тестирований, позволяющих определить эффективность работы модуля Distribution. Средняя нагрузка на ресурсы центрального процессора в деактивированном/активированном режимах приравнивается к 17,54/1,16 %. Средняя разница в нагрузке составляет 11,15 единицы. Это дает возможность запуска вычислительных процессов различной ресурсоемкости с последующим повышением производительности и рациональным использованием физических ресурсов. Потребление оперативной памяти в активированном режиме составляет 0,055 %. Данная загрузка является незначительной и не вли- яет на работоспособность физических серверов. Средняя загруженность твердотельного накопи- теля (SSD) колеблется от 0 до 0,066 %. Средняя разница в нагрузке приравнивается к 0,691 единицы. Высокая производительность и низкая нагрузка на вычислительные ресурсы каждого физического сервера в кластере позволяют не только более рационально использовать вычислительную мощность, но и параллельно запускать ресурсоемкие процессы, решающие определенные задачи.
Таким образом, проанализирована и исследована рабочая среда каждого физического сервера в кластере. Удобство в управлении и равномерное распределение нагрузки на вычислительных ресурсах каждого сервера в кластере позволили организовать стабильную работу.
Литература
1. Пальчевский Е.В., Халиков А.Р. Равномерное распределение нагрузки аппаратно-программного ядра в UNIX-системах // Тр. ИСП РАН. 2016. Т. 28. Вып. 1. С. 93–102. DOI: 10.15514/ ISPRAS-2016-28(1)-6.
2. Цымблер М.Л., Мовчан А.В. Обнаружение подпоследовательностей во временных рядах // Открытые системы. СУБД. 2015. № 2. С. 42–43.
3. Иванова Е.В., Соколинский Л.Б. Декомпозиция операций пересечения и соединения на основе доменно-интервальной фрагментации колоночных индексов // Вестн. ЮУрГУ. Сер.: Вычислительная математика и информатика. 2015. Т. 4. № 1. С. 44–56. DOI: 10.14529/cmse150104.
4. Танана В.П., Бельков С.И. Конечноразностная аппроксимация метода регуляризации А.Н. Тихонова N-го порядка // Вестн. ЮУрГУ. Сер.: Вычислительная математика и информатика. 2015. Т. 4. № 1. С. 86–98. DOI: 10.14529/cmse150108.
5. Пальчевский Е.В., Халиков А.Р. Автоматизированная система обработки данных в UNIX-подобных системах // Программные продукты и системы. 2017. Т. 30. № 2. С. 227–234. DOI: 10.15827/0236-235X.030.2.227-234.
6. Лаврищева Е.М., Петренко А.К. Моделирование семейств программных систем // Тр. ИСП РАН. 2016. Т. 28. Вып. 6. С. 49–64. DOI: 10.15514/ISPRAS-2016-28(6)-4.
7. Бурдонов И.Б., Косачев А.С. Система автоматов: композиция по графу связей // Тр. ИСП РАН. 2016. Т. 28. Вып. 1. С. 131–150. DOI: 10.15514/ISPRAS-2016-28(1)-8.
8. Shteinberg О.B. Circular shift of loop body – programme transformation, promoting parallelism // Вестн. ЮУрГУ: Математическое моделирование и программирование. 2017. Т. 10. № 3. С. 120–132 (англ.). DOI: 10.14529/mmp170310.
9. Посыпкин М.А., Тант Син Си Ту. О распараллеливании метода динамического программирования для задачи о ранце // Intern. J of Open Information Technologies. 2017. Т. 5. № 7. С. 1–5 (рус.).
10. Овчаренко О.И. Об одном подходе к распараллеливанию метода циклической редукции для решения систем уравнений с трехдиагональной матрицей // Современные тенденции развития науки и производства: сб. матер. III Междунар. конф. 2016. С. 152–155.
11. Пелипец А.В. Распараллеливание итерационных методов решения систем линейных алгебраических уравнений на реконфигурируемых вычислительных системах // Суперкомпьютерные технологии (СКТ-2016): матер. 4-й Всерос. науч.-технич. конф. 2016. С. 194–198.
12. Белим С.В., Кутлунин П.Е. Выделение контуров на изображениях с помощью алгоритма кластеризации // Компьютерная оптика. 2015. Т. 39. № 1. С. 119–124. DOI: 10.18287/0134-2452-2015-39-1-119-124.
References
- Palchevsky E.V., Khalikov A.R. Uniform load distribution of a hardware-software core in UNIX systems. Proc. of ISP RAS. 2016, vol. 28, iss. 1, pp. 93–102 (in Russ.). DOI: 10.15514/ISPRAS-2016-28(1)-6.
- Tsymbler M.L., Movchan A.V. Detection of subsequences in time series. Open systems. DBMS. 2015, no. 2, pp. 42–43 (in Russ.).
- Ivanova E.V., Sokolinsky L.B. Decomposition of operations of intersection and connection based on domain and interval fragmentation of columnar indexes. Bulletin of South Ural State Univ. Series: Mathematical Modelling, Programming & Computer Software. 2015, vol. 4, no. 1, pp. 44–56 (in Russ.). DOI: 10.14529/cmse150104.
- Tanana V.P., Belkov S.I. Finite-difference approximation of Tikhonov’s regularization method of the Nth order. Bulletin of South Ural State Univ. Series: Computational Mathematics and Software Engineering. 2015, vol. 4, no. 1, pp. 86–98 (in Russ.). DOI: 10.14529/cmse150108.
- Palchevsky E.V., Khalikov A.R. Automated data processing system in UNIX-like systems. Software & Systems. 2017, vol. 30, no. 2, pp. 227–234 (in Russ.). DOI: 10.15827/0236-235X.030.2.227-234.
- Lavrishcheva E.M., Petrenko A.K. Simulation of program families. Proc. of ISP RAS. 2016, vol. 28, iss. 6, pp. 49–64 (in Russ.). DOI: 10.15514/ISPRAS-2016-28(6)-4.
- Burdonov I.B., Kosachev A.S. System of automatic machines: a bond graph composition. Proc. of ISP RAS. 2016,
vol. 28, iss. 1, pp. 131–150 (in Russ.). DOI: 10.15514/ISPRAS-2016-28(1)-8.
- Shteinberg O.B. Circular shift of the loop body – programme transformation, promoting parallelism. Bulletin of the South Ural State Univ. Series: Mathematical Modelling, Programming & Computer Software. 2017, vol. 10, no. 3, pp. 120–132 (in Russ.). DOI: 10.14529/mmp170310.
- Posypkin M.A., Si Thu Thant Sin. On the parallelization of dynamic programming method for knapsack problem. Intern. J. of Open Information Technologies. 2017, vol. 5, no. 7, pp. 1–5.
- Ovcharenko O.I. On one approach to parallelizing the method of cyclic reduction for solving systems of tridiagonal matrix equations. Current Trends in the Development of Science and Production: Proc. 3rd Intern. Practical Conf. Kemerovo, 2016, pp. 152–155 (in Russ.).
- Pelipets A.V. Parallelization of iterative methods for solving systems of linear algebraic equations on reconfigurable computing systems. Supercomputer Technologies (SKT-2016): Proc. 4th All-Russian Sci. and Tech. Conf. Rostov-on-Don, SFedU Publ., 2016, pp. 194–198 (in Russ.).
- Belim S.V., Kutlunin P.E. Image edge detection using the clustering algorithm. Computer Optics. 2015, vol. 39,
no. 1, pp. 119–124 (in Russ.). DOI: 10.18287/0134-2452-2015-39-1-119-124.




 (4)
(4)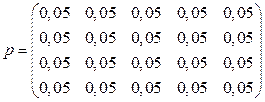 , (5)
, (5) (6)
(6)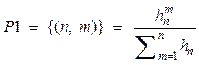 , (8)
, (8) – интенсивная обработка заявок (сетевых пакетов/вычислительных процессов), где m – количество сетевых пакетов, n – количество вычислительных процессов. Измерение обработки происходит многопоточно (шт./с). Это позволяет добиться более высокого процента успешных обработок заявок по переносу вычислительных процессов по кластеру. Далее необходимо узнать вероятность занятых мест в очереди на пернос процессов:
– интенсивная обработка заявок (сетевых пакетов/вычислительных процессов), где m – количество сетевых пакетов, n – количество вычислительных процессов. Измерение обработки происходит многопоточно (шт./с). Это позволяет добиться более высокого процента успешных обработок заявок по переносу вычислительных процессов по кластеру. Далее необходимо узнать вероятность занятых мест в очереди на пернос процессов: , (9)
, (9) (получена при стохастическом моделировании различных процессов СМО) [12], где R0 – количество заявок на обработку; P0 – состояние системы; P – вероятность перехода; K0 – лимит на количество заявок; L0 – количество заявок в обработке. Схема работы переноса вычислительных процессов (с применением цепей Маркова) по кластеру показана на рисунке 4.
(получена при стохастическом моделировании различных процессов СМО) [12], где R0 – количество заявок на обработку; P0 – состояние системы; P – вероятность перехода; K0 – лимит на количество заявок; L0 – количество заявок в обработке. Схема работы переноса вычислительных процессов (с применением цепей Маркова) по кластеру показана на рисунке 4.

 , (11)
, (11)