В современных инфокоммуникационных системах и сетях обеспечение высокой надежности [1, 2], отказоустойчивости, безопасности и производительности при минимизации задержек передачи данных в значительной мере зависит от организации метода множественного доступа [3, 4].
Как объект исследований централизованные системы передачи данных состоят из абонентских станций и базовой станции, обслуживающей абонентские станции. Передача данных между ними происходит по восходящему и нисходящему каналам. Восходящий канал предназначен для передачи от абонентской станции до базовой, при этом абонентские станции друг друга «не слышат». Взаимодействие между ними осуществляется через базовую станцию. Передача данных от базовой станции к абонентской осуществляется по нисходящему каналу, причем в широковещательном режиме, поэтому все абонентские станции ее «слышат».
В системах множественного доступа передача данных основана на соперничестве станций за общую среду передачи, при этом каждый узел, не имеющий задолженности, передает пакет, рискуя попасть в случайные конфликты [5]. По данным исследований [6], в существующих системах множе- ственного доступа с применением алгоритма ALOHA имеется проблема низкой пропускной спо- собности и низкой надежности. Алгоритм случайного множественного доступа (СМД) решает задачи доступа к каналу и разрешения конфликтов. В широко распространенных алгоритмах семейства ALOHA (двоичная экспоненциальная отсрочка, множественный доступ с прослушиванием, тактированная ALOHA) алгоритм разрешения отсутствует [7]. Для алгоритмов семейства ALOHA характерна простота реализации, но отмечается низкая пропускная способность канала. В модели СМД централизованных сетей рассматривается только конкурентный интервал. В зависимости от сложившейся ситуации в канале передачи в определенном промежутке времени возможны три ситуации в слотах – успех, пусто, конфликт [8].
Доказано, что использование древовидных алгоритмов показывает хорошую производительность по сравнению с алгоритмами семейства ALOHA [7] за счет того, что древовидные алгоритмы включают в себя, кроме алгоритма доступа к каналу, и алгоритмы разрешения конфликтов. Недостаток древовидных алгоритмов – сложная вычислительная реализация [9].
В данной работе предлагается модифицированный алгоритм с погашением интерференции, который предусматривает использование дополнительных ячеек памяти и пропуск конфликтных сигналов в нижних окнах. Он основан на идее поиска в множестве принятых сигналов ортогонального подмножества, позволяющего одновременно извлечь все множество конфликтных сигналов. Алгоритм использует полный перебор и потому обладает значительной вычислительной сложностью, в силу этого требуется оценить границу для пропускной способности системы при использовании предложенного модифицированного древовидного алгоритма.
Описание алгоритма
Предлагается модифицированный алгоритм из семейства ALOHA. Его анализ основан на следующих известных предположениях, описывающих модель множественного доступа с последовательным подавлением помех.
1. Канал разделен на временные интервалы фиксированной длины. Каждому пользовате- лю разрешается начинать передачу в начале временного интервала. Все пакеты имеют одина- ковую длину, равную одному временному ин- тервалу.
2. Безошибочный прием сигнала: слот принимается либо как пустой, успешный, либо как слот-конфликт в зависимости от количества передаваемых пакетов: ноль, один или несколько.
3. Существует бесконечный набор пользователей, генерирующих пакеты в соответствии с процессом Пуассона (где каждый пакет соответствует новому пользователю).
4. Безошибочный ответ. В конце каждого окна базовая станция передает статус конфликта: либо успех (конфликт разрешен успешно), либо нет.
Основная идея предлагаемой модификации состоит в следующем: при разрешении конфликта некоторой кратности N осуществляется поиск подмножества из N линейно независимых сигналов, переданных в процессе разрешения данного конфликта. В этом отношении существует некоторое сходство с алгоритмами беспроводного множественного доступа, введенными в [10–12]. Эти алгоритмы способны разрешать конфликт пользователей K с помощью методов разделения источников. Более конкретно: каждый из пользователей K повторно передает свой пакет в каждом последующем слоте, пока базовая станция не объявит о завершении текущего периода разрешения конфликта.
Основное отличие предлагаемой модификации алгоритма заключается в том, что пакеты декодируются с использованием абстрактной концепции вычитания/сложения сигнала, и предполагается, что множественность конфликта не может быть об- наружена. Более того, каждое сообщение-участник конфликта покидает систему в самом его конце. В древовидных алгоритмах сообщения покидают систему по мере разрешения конфликта, а не только в самом конце.
При модификации алгоритма множественного доступа в исходящий сигнал от каждого абонента добавляется служебная информация о предыдущих попытках передать сигнал.
Каждый конфликтный период представляет собой кадр, содержащий M слотов равной продолжительности, где M фиксировано, и набор из N пользователей для связи с базовой станцией (BS), которая действует как общий приемник. В начале конфликта каждый пользователь самостоятельно генерирует пакет, который должен быть передан с вероятностью pa, где pa < 1. Число активных пользователей в конфликтном периоде Na является случайной распределенной величиной со средним значением Na = pa N.
Время, прошедшее от начального столкновения до момента, когда пакеты были успешно переданы, называется периодом разрешения конфликтов (CRP). Таким образом, когда используется режим заблокированного доступа, новые поступления блокируются до тех пор, пока не закончится CRP, в течение которого они прибыли. Блокируемые поступления будут участвовать в следующем CRP.
Такое поведение повторяется для каждого из последующих слотов, пока приемник не получит сообщение SUCCESS, воспринимаемое как обратная связь, указывающая, что все пакеты успешно декодированы, а значит, завершен CRP. Для N больших это правило часто приводит к последовательности столкновений, так как вероятность успешной передачи (или пустого окна) уменьшается экспоненциально с ростом N.
Существует одно исключение из этого правила передачи: в начале каждого CRP пользователи обязаны передавать свой пакет со служебной информацией о предыдущих попытках передать сигнал. Важнейшей причиной этого правила является то, что нужно определить, были ли все пакеты, участвующие в текущем CRP, декодированы из переданных сигналов. Иначе невозможно установить всех участников конфликта и, соответственно, определить его завершение.
Пусть в текущем конфликте участвуют N абонентов (кратность конфликта N заранее неизвестна). Установим в соответствие si-му сигналу, принятому базовой станцией, бинарный вектор-столбец si ∈ {1, 0}N. Единица на позиции j вектора-столбца si означает, что в окне i абонент j осуществлял передачу. Таким образом, s0 – это вектор из N единиц, так как в первом окне конфликта все участвующие абоненты осуществляют передачу. Если некоторый вектор-столбец si содержит ровно одну единицу на позиции j, то абонент j осуществил успешную передачу сигнала.
Предположим, что с начала процедуры разрешения конфликта было передано m ≥ N сигналов, а также, что N из этих m сигналов соответствуют множеству линейно независимых вектор-столбцов si1 ,..., siN, где 1 = i1 < i1< ... < iN = m. Пусть M есть N × N – матрица, составленная из вектор-столбцов si1, ..., siN (k-й столбец которой есть вектор-столбец sik). M состоит из линейно независимых столбцов, следовательно, обратима.
Предположим теперь, что известны кратность конфликта N, набор индексов i1, ..., xN-1 и соответствующая им матрица M. В случае, если M–1 содержит только целые числа, можно восстановить исходные сигналы, решив систему уравнений s = xM относительно x или x= sM–1, гдe s – это множество принятых на базовой станции сигналов в окнах i1, ..., iN.
В качестве примера проанализируем определенный конфликт кратности N = 5. Введем в рассмотрение сигналы от четырех абонентов s = (A, B, C, D, E). Пусть в первом, втором, третьем, четвертом и пятом окнах получены следующие смеси сигналов: si1= A + B + C + D + E, si2 = A + C, si3 = A + + B, si4 = D, si5 = E. Описанная ситуация схематично изображена на рисунке. Восстановление сигналов (A, B, C, D, E) эквивалентно нахождению решения системы уравнений:
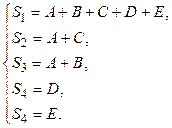
Соответствующая матрица M и ее обратная матрица M–1 следующие:
 ,
,  .
.
 Так, можно получить A как – s i1+ si2 + si3 + si4 + + si5 = – A – B – C – D – E + A + C + A + B + D + E = = A. Иными словами, вектор-столбцы М-1 обеспечивают базовую станцию необходимыми коэффициентами и операциями для процедуры погашения интерференции.
Так, можно получить A как – s i1+ si2 + si3 + si4 + + si5 = – A – B – C – D – E + A + C + A + B + D + E = = A. Иными словами, вектор-столбцы М-1 обеспечивают базовую станцию необходимыми коэффициентами и операциями для процедуры погашения интерференции.
В общем случае коэффициенты в матрице М–1 могут быть любыми рациональными числами. Если умножим каждый элемент матрицы на ее определитель, получим целые коэффициенты. В этом случае решением системы уравнений будут помноженные на определитель матрицы (целое число для двоичной матрицы) исходные абонентские сигналы. Согласно допущениям алгоритма, базовая станция в состоянии корректно декодировать сигнал aS, где а целое. Положив а = |М–1| для каждого сигнала, базовая станция, таким образом, окажется в состоянии восстановить каждый принятый сигнал.
Задача нахождения неизвестных N, i1, ..., in, и М решается с помощью полного перебора по всем возможным вариантам этих значений при приеме каждого очередного сигнала. Перебирая все возможные обратимые бинарные матрицы М и решая x = s |М| М–1, базовая станция проверяет, соответствует ли x множеству успешно переданных сигналов, и при обнаружении соответствия посылает уведомление об успешном разрешении конфликта.
Можно показать, что подобная процедура позволяет установить множество переданных сигналов с точностью до перестановки.
Время разрешения конфликта LN в предложенном алгоритме равняется среднему количеству попыток, требуемых для получения N линейно независимых векторов [10]. Среднее время разрешения конфликта прямо пропорционально его кратности:
 ,
,

При N, стремящемся к бесконечности, второе слагаемое предыдущего уравнения сходится к константе 1 • 606695. Таким образом, количество окон, необходимых для восстановления конфликтных сигналов, линейно зависит от количества этих сигналов:  , пропускная способность для данного алгоритма равна
, пропускная способность для данного алгоритма равна  .
.
Заключение
В работе предложен алгоритм множественного доступа для канала с погашением интерференции. Основная идея подхода состоит в том, чтобы разрешить конфликт некоторой кратности N, собирая достаточные (≥ N) линейные комбинации этих N пакетов, так что, эти N отдельных пакетов могут быть извлечены путем идентификации подмножества из N линейных независимых сигналов. Основное отличие данной работы в том, что от каждого абонента происходит добавление в исходящий сигнал служебной информации о предыдущих попытках передать сигнал. Кроме того, пакеты декодируются с использованием абстрактной концепции вычитания/сложения сигнала. Более того, каждое сообщение-участник конфликта покидает систему в самом его конце. В древовидных алгоритмах сообщения покидают систему по мере разрешения конфликта, а не только в самом конце. На практике данный алгоритм можно применить для автоматизации склада: автоматически собирать информацию в масштабе реального времени о поступлении и реализации товаров и сокращении времени на все логические операции.
Разработанный алгоритм обеспечивает максимальную пропускную способность (Maximum Stable Througput, MST, Rc), равную 1. Наилучший из предложенных ранее алгоритмов – алгоритм Гионнакеса (Successive Interference Cancellation Tree Algorithm, SICTA), обеспечивающий максимальную пропускную способность Rc = 0.693.
Литература
1. Sorin D. Fault Tolerant Computer Architecture. Morgan & Claypool, 2009, 103 p.
2. Богатырев В.А., Богатырев С.В. Критерии оптимальности многоустойчивых отказоустойчивых компьютерных систем // Науч.-технич. вестн. СПб гос. ун-та информ. технологий, механики и оптики. 2009. № 5. С. 92–98.
3. Коломойцев В.С. Оценка эффективности и обоснование выбора структурной организации системы многоуровневого защищенного доступа к ресурсам внешней сети // Информация и космос. 2015. № 3. С. 71–79.
4. Богатырев В.А., Богатырев С.В., Богатырев А.В. Оптимизация древовидной сети с резервированием коммутационных узлов и связей // Телекоммуникации. 2013. № 2. С. 42–48.
5. Parshutina S.A. Models to support design of highly reliable distributed computer systems with redundant processes of data transmission and handling. Proc. Intern. Conf. IT&QM&IS, 2017, pp. 96–99. DOI:10.1109/itmqis.2017.8085772.
6. Кирьянов А.Г., Ляхов А.И., Хоров Е.М. Модель передачи мультимедийных потоков реального времени при помощи детерминированного метода доступа // Информационные процессы. 2014. Т. 14. № 3. С. 197–213.
7. Цыбаков Б.C., Михайлов В.А. Свободный синхронный доступ пакетов в широковещательный канал с обратной связью // Пробл. передачи информ. 1978. Т. 22. № 4. С. 32–59.
8. Андреев С.Д. Централизованное управление множественным доступом в сетях передачи информации при высокой загрузке: дис. канд. технич. наук. СПб, 2009. 182 с.
9. Никоненко Н.Д. Древовидный алгоритм вычисления условных математических ожиданий // Современные наукоемкие технологии. 2017. № 2. С. 48–52.
10. Peeters G.T., Van Houdt B. On the capacity of a random access channel with successive interference cancellation. Proc. IEEE ICCW, 2015, pp. 2051–2056. DOI: 10.1109/TCOMM.2010.093010. 090222.
11. Paolini E., Stefanovic C., Liva G., Popovski P. Coded random access: applying codes on graphs to design random access protocols. IEEE Communications Magazine, 2015, vol. 53, no. 6, pp. 144–150. DOI: 10.1109/MCOM.2015.7120031.
12. Houdt B. Van, Peeters G.T. FCFS tree algorithms with interference cancellation and single signal memory requirements. Telecommunications, Proc. ICT 2008, pp. 1–6. DOI: 10.1109/ ICTEL.2008.4652691.
13. Богатырев В.А., Богатырев А.В. Функциональная надежность систем реального времени // Науч.-технич. вестн. СПб гос. ун-та информ. технологий, механики и оптики. 2013. № 4. С. 150–151.
14. Кобляков В.А. Управление множественным доступом в централизованных сетях передачи данных: дис. канд. технич. наук. СПб, 2016, 19 с.
15. Новиков Е.А., Зиннуров С.Х. Модель гибкого обслуживания трафика сложной структуры и алгоритм оперативного резервирования дополнительных каналов в земных станциях спутниковой связи // Системы управления, связи и безопасности. 2017. № 1. С. 98–115.
16. Топорков И.С., Ковальский А.А., Зиннуров С.Х. Модель и алгоритм управления процессом резервирования ресурса сети спутниковой связи при обслуживании разнородного нестационарного трафика // Изв. Ин-та инженерной физики. 2016. Т. 1. № 39. С. 37–47.
References
- Sorin D. Fault Tolerant Computer Architecture. Morgan & Claypool Publ., 2009, 103 p.
- Bogatyrev V.A., Bogatyrev S.V. Optimality criteria of multilevel failure-safe computer systems. Scientific and Technical J. of Information Technologies, Mechanics and Optics. 2009, no. 5, pp. 92–98 (in Russ.).
- Kolomoytsev V.S. Estimation of efficiency and rationale for the selection of the structural organization of the system of multi-level secure access to external network resources. Information and Space. 2015, no. 3, pp. 71–78 (in Russ.).
- Bogatyrev V.A., Bogatyrev S.V., Bogatyrev A.V. Tree network optimization with redundant switching nodes and connections. Telecommunications. 2013, no. 2, pp. 42–48 (in Russ.).
- Parshutina S.A. Models to support design of highly reliable distributed computer systems with redundant processes of data transmission and handling. 2017 Intern. Conf. “Quality Management, Transport and Information Security, Information Technologies” (IT&QM&IS). 2017, pp. 96–99. DOI:10.1109/itmqis.2017.8085772.
- Kiryanov A.G., Lyakhov A.I., Khorov E.M. Model of the transfer of real-time multimedia streams using a deterministic access method. Information Processes. 2014, vol. 14, no. 3, pp. 197–213 (in Russ.).
- Tsybakov B.C., Mikhaylov V.A. Free synchronous access of packets to a broadcast channel with feedback. Problems of Information Transmission. 1978, vol. 22, no. 4, pp. 32–59 (in Russ.).
- Andreev S.D. Centralized Management of Multiple Access in High-Load Information Networks. PhD Thesis. St. Petersburg, 2009, 182 p.
- Nikonenko N.D. The tree algorithm for calculation of conditional mathematical expectations. Modern Science Technologies. 2017, no. 2, pp. 48–52 (in Russ.).
- Peeters G.T., Van Houdt B. On the capacity of a random access channel with successive interference cancellation. IEEE Intern. Conf. on Communication Workshop (ICCW), 2015. 2015, pp. 2051–2056. DOI: 10.1109/TCOMM.2010.093010.
090222.
- Paolini E., Stefanovic C., Liva G., Popovski P. Coded random access: applying codes on graphs to design random access protocols. IEEE Comm. Magazine. 2015, vol. 53, no. 6, pp. 144–150. DOI: 10.1109/MCOM.2015.7120031.
- Van Houdt B., Peeters G.T. FCFS tree algorithms with interference cancellation and single signal memory requirements. Intern. Conf. on Telecommunications, ICT 2008. 2008, pp. 1–6. DOI:10.1109/ICTEL.2008.4652691.
- Bogatyrev V.A., Bogatyrev A.V. Functional reliability of real-time systems. Scientific and Technical J. of Information Technologies, Mechanics and Optics. 2013, no. 4, pp. 150–151 (in Russ.).
- Koblyakov V.A. Management of Multiple Access in Centralized Data Networks. PhD Thesis. St. Petersburg, 2016,
19 p.
- Novikov E.A., Zinnurov S.Kh. Flexible service model of complex traffic and real-time algorithm of channel reserve for satellite earth stations. Systems of Control, Communication and Security. 2017, no. 1, pp. 98–115 (in Russ.).
- Toporkov I.S., Kovalsky A.A., Zinnurov S.Kh. Model and algorithm of management of process of reservation of a resource of a network of satellite communication at service of the diverse non-stationary traffic. Proc. of Institute of Engineering Physics. 2016, vol. 1, no. 39, pp. 37–47 (in Russ.).



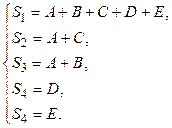
 ,
,  .
.
 ,
,
 , пропускная способность для данного алгоритма равна
, пропускная способность для данного алгоритма равна  .
.