Выравнивание различных тестов на единую метрическую шкалу
| Хлебников В.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Отображение результатов тестирования по разным тестам и в разные годы на единой метрической шкале возможно лишь в том случае, если тестовые задания разных лет имеют соизмеримые количественные характеристики трудностей. Создание соответствующей метрической шкалы предполагает калибровку тестовых заданий разных лет по единой научно обоснованной схеме и накопление определенного множества заданий, известные трудности которых и задают индексы нужной шкалы. Частным случаем является задача выравнивания на единую шкалу различных вариантов одного и того же теста. Решение указанной проблемы должно выработать как рекомендации по созданию тестов для калибровки заданий разных лет, так и рекомендации по математической обработке таких тестов. Данная работа посвящена совместной математической обработке различных тестов одинаковой содержательной валидности. Уравнения связи и взвешенные уравнения измерений Результаты тестирования по всем тестам, разработанным для калибровки заданий, мы рекомендуем обрабатывать совместно. Предположим, что обработке подлежат T различных тестов (или вариантов теста), содержащих по Нами получены соответствующие уравнения связи, то есть уравнения, связывающие то, что мы ищем, с тем, что мы измеряем. Они имеют вид:
где введено обозначение
j=0,1,2,...,K-1; g=0,1,2,...,K-1, но g>j. Здесь Так как обработке подлежат K заданий, то количество m таких уравнений равно числу сочетаний из K по 2, то есть m= Если среди всех N испытуемых имеются такие, которые выполняли и задание j, и задание g, то вместо модельной величины (2), содержащей неизвестные вероятности, естественно воспользоваться ее доступной статистической оценкой вида
Здесь Заметим, что одно и то же расстояние Итак, искомая разность параметров
Вес правой части уравнения равен
где Правая часть уравнений измерений (4) может быть получена лишь в том случае, когда имеются испытуемые, работавшие и над заданием j, и над заданием g. В противном случае величина Количество реальных уравнений измерений обычно равно Количество независимых неизвестных в этих уравнениях еще меньше и определяется числом K-1. Поэтому всегда имеются избыточные измерения, общее количество которых обычно равно Точность измеренного значения
где Соответствующий вес обратно пропорционален указанной дисперсии и, согласно (5) и (6), определяется формулой
где j=0,1,2,...,K-1 и g=0,1,2,...,K-1 при j - дисперсия единицы веса. Если какие-либо значения Для определенности примем вес измерения
и, таким образом, мы можем вычислить по формулам (6)-(8) конкретные значения весов всех измерений. Решение уравнений измерений методом наименьших квадратов Для тестов, состоящих в общей сложности из K заданий, система уравнений связи насчитывает
где j=0,1,2,...,K-1; g=0,1,2,...,K-1; j Перепишем (9) следующим образом:
Здесь
Для общности рассуждений записываются уравнения связи (9) в форме (10) и в том случае, когда их правая часть Если ошибками
оказывается несовместной и любые ее решения
Система таких уравнений называется системой уравнений поправок. Обработка каждого теста (варианта теста) по отдельности Задание с номером 0, задающее начало отсчета шкалы каждого теста, следует выбирать среди узловых заданий. Сначала надо решать систему нормальных уравнений, не обращая внимания на наличие узловых заданий. Не пересекаются и множества испытуемых, работавших над различными тестами. Для выравнивания вычисленных оценок Как при строгом, так и при приближенном подходе все элементы матрицы Q вычисляются относительно единого начала, используя тот факт, что задания с номером 0 всех тестов являются узловыми. Итак, общая проблема калибровки тестовых заданий и выравнивания их характеристик на единую шкалу трактуется нами как задача на условный экстремум. При этом предложение обрабатывать совместно много тестов (или много вариантов одного теста) не приводит к существенному увеличению объема требуемых вычислений и может быть реализовано в рамках традиционной технологии обработки результатов тестирования. |
http://swsys.ru/index.php?id=453&lang=%29&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Интеллектуальная поддержка реинжиниринга конфигураций производственных систем
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам

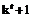 заданий, где верхний индекс t здесь и в дальнейшем обозначает номер теста (или номер варианта), t=1,2,...,T, а номера заданий в каждом тесте начинаются с нуля. Количество испытуемых, работавших над тестом с номером t равно
заданий, где верхний индекс t здесь и в дальнейшем обозначает номер теста (или номер варианта), t=1,2,...,T, а номера заданий в каждом тесте начинаются с нуля. Количество испытуемых, работавших над тестом с номером t равно 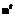 . Общее количество заданий (дихотомического типа) будем обозначать буквой K=
. Общее количество заданий (дихотомического типа) будем обозначать буквой K=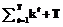 (хотя не все задания являются различными в силу перекрытий тестов), а общее количество участников тестирования - буквой N=
(хотя не все задания являются различными в силу перекрытий тестов), а общее количество участников тестирования - буквой N=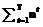 .
.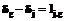 , (1)
, (1)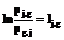 , (2)
, (2)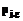 - вероятность того, что некоторый испытуемый с уровнем подготовленности
- вероятность того, что некоторый испытуемый с уровнем подготовленности  верно выполнит задание j, а при выполнении задания g ошибется;
верно выполнит задание j, а при выполнении задания g ошибется; 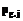 - вероятность того, что тот же испытуемый верно выполнит задание g, тогда как задание j окажется выполненным им ошибочно.
- вероятность того, что тот же испытуемый верно выполнит задание g, тогда как задание j окажется выполненным им ошибочно.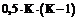 .
.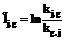 . (3)
. (3) - количество испытуемых, верно выполнивших задание с номером j, но не выполнивших задание с номером g;
- количество испытуемых, верно выполнивших задание с номером j, но не выполнивших задание с номером g; 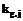 - количество испытуемых, верно выполнивших задание с номером g, но не выполнивших задание с номером j; "~" – результат измерения соответствующей величины. Числа
- количество испытуемых, верно выполнивших задание с номером g, но не выполнивших задание с номером j; "~" – результат измерения соответствующей величины. Числа 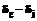 измеряется каждым испытуемым i=1,2,..., работавшим над заданиями j и g, вне зависимости от его уровня подготовленности
измеряется каждым испытуемым i=1,2,..., работавшим над заданиями j и g, вне зависимости от его уровня подготовленности 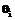 . Другими словами, объект измерений (2) остается постоянным для каждого испытуемого и может быть оценен формулой (3) без каких-либо дополнительных гипотез.
. Другими словами, объект измерений (2) остается постоянным для каждого испытуемого и может быть оценен формулой (3) без каких-либо дополнительных гипотез. и
и  для непосредственного измерения недоступна, но можно измерить ее функцию
для непосредственного измерения недоступна, но можно измерить ее функцию 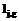 вида (2). Результат измерения
вида (2). Результат измерения 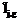 определяется числом (3). Его дисперсия
определяется числом (3). Его дисперсия 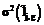 зависит от чисел
зависит от чисел 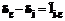 . (4)
. (4)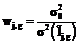 , (5)
, (5)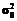 обозначает дисперсию такого измерения, вес которого условно принят за единицу.
обозначает дисперсию такого измерения, вес которого условно принят за единицу.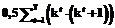 , что меньше количества уравнений связи
, что меньше количества уравнений связи 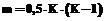 , поскольку задания разных тестов одними и теми же испытуемыми обычно не выполняются.
, поскольку задания разных тестов одними и теми же испытуемыми обычно не выполняются.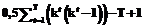 .
. определяется дисперсией
определяется дисперсией , (6)
, (6)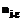 - количество испытуемых, работавших над заданиями j и g; относительная частота
- количество испытуемых, работавших над заданиями j и g; относительная частота 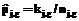 является оценкой неизвестной вероятности
является оценкой неизвестной вероятности  является оценкой неизвестной вероятности
является оценкой неизвестной вероятности 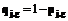 .
.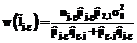 , (7)
, (7)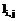 не удалось измерить, то соответствующий вес
не удалось измерить, то соответствующий вес 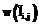 принимается равным нулю.
принимается равным нулю. за единицу. Это означает, что
за единицу. Это означает, что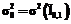 (8)
(8)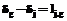 , (9)
, (9)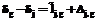 . (10)
. (10) - истинная случайная ошибка такого измерения с нулевым математическим ожиданием и дисперсией:
- истинная случайная ошибка такого измерения с нулевым математическим ожиданием и дисперсией: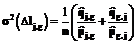 . (11)
. (11) пренебречь, то соответствующая система уравнений измерений
пренебречь, то соответствующая система уравнений измерений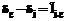 (12)
(12) приводят к необходимости добавить к правым частям
приводят к необходимости добавить к правым частям  , являющиеся уклонениями от результатов непосредственных измерений:
, являющиеся уклонениями от результатов непосредственных измерений: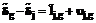 , j
, j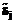 на единую шкалу надо составить и решить систему уравнений. Количество таких уравнений равно количеству пар узловых заданий. При этом возможны два подхода – строгий и приближенный.
на единую шкалу надо составить и решить систему уравнений. Количество таких уравнений равно количеству пар узловых заданий. При этом возможны два подхода – строгий и приближенный.