Одним из приоритетных направлений в области проектирования новых образцов вооружения и военной техники на основе современных достижений науки и техники является создание наземных робототехнических комплексов военного назначения (НРТК ВН), предназначенных для решения широкого спектра боевых (тактических) и обеспечивающих задач. Результаты теоретических иссле- дований и практического применения НРТК ВН свидетельствуют о высокой степени готовности отдельных образцов к использованию в составе групп [1]. Групповое применение рассматривается в качестве следующего эволюционного этапа повышения возможностей робототехнических комплексов, в ходе которого планируется согласовать совместные действия машин и объединить их в группы под управлением операторов. При этом одной из центральных проблем группового управления остается формирование тактической задачи оператором и доведение ее до группы.
Как правило, формирование тактической задачи для группы роботов осуществляется с использованием специального языка программирования текстового типа MCL (Mission Control Language) [2] или BML (Battle Management Language) [3]. Сформированная таким образом задача затем транс- лируется в сеть Петри, являющуюся удобным формальным представлением управляющего ал- горитма при групповом взаимодействии робо- тов [2, 4–6]. Недостатками такого подхода к способу формирования тактической задачи являются необходимость наличия у оператора навыков программирования и отсутствие автоматизированного ввода координат маршрутов, рубежей, районов действия и т.п., то есть привязки задачи к карте. Отличным от указанного способа является пред- ложенный в работе [7] подход к формализации тактической задачи для группы НРТК ВН, заклю- чающийся в использовании геоинформационной системы (ГИС) [8] в качестве графической основы для формирования задачи с помощью условных тактических знаков и ее дальнейшей трансляции в эквивалентную сеть Петри. В настоящей работе описан разработанный транслятор, который позволяет преобразовать тактическую задачу, заданную с помощью нанесенных на электронную карту условных тактических знаков, в эквивалентную сеть Петри.
Задача проектирования транслятора тактической задачи в сеть Петри
Тактическую задачу, формируемую оператором на карте для группы НРТК ВН, можно представить в виде ориентированного мультиграфа G = (V, A) c конечным числом вершин V и дуг A, где A Í V ´ V. Орграф состоит из рубежей (исходных, регулирования, действия) и условных тактических знаков, кодирующих групповые действия. Исходные рубежи служат для определения начального состава подгрупп и являются условными знаками, инициализирующими начало выполнения задачи. Исходных рубежей может быть несколько. До выполнения тактической задачи у оператора в распоряжении имеется только одна группа, состоящая из N единиц НРТК ВН.
Рубежи регулирования предназначены для синхронизации действий отдельных подгрупп – перераспределения НРТК между ними. Каждый рубеж vi в задаче является вершиной (viÎV, 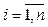 , n = ½V½), а групповое действие aj – дугой (aj Î A,
, n = ½V½), а групповое действие aj – дугой (aj Î A, , m = ½A½). Дуги могут быть кратными: при выполнении одного и того же действия между двумя рубежами несколькими разными подгруппами. Каждый из рубежей имеет свой номер, указываемый в соответствующей семантической характеристике (атрибуте знака в ГИС) и отображаемый на электронной карте. Нумерация начинается с исходных рубежей и для исключения неоднозначности ведется оператором на карте слева направо в направлении действия группы.
, m = ½A½). Дуги могут быть кратными: при выполнении одного и того же действия между двумя рубежами несколькими разными подгруппами. Каждый из рубежей имеет свой номер, указываемый в соответствующей семантической характеристике (атрибуте знака в ГИС) и отображаемый на электронной карте. Нумерация начинается с исходных рубежей и для исключения неоднозначности ведется оператором на карте слева направо в направлении действия группы.
Задача транслятора заключается в преобразовании исходного мультиграфа G в сеть Петри С = (P, T, I, O), где P – конечное множество позиций, T – конечное множество переходов, P Ç T = Æ, I – входная функция, I: T® P, О – выходная функция, О: T ® P.
Описание транслятора тактической задачи
В соответствии с приведенной постановкой далее дано описание транслятора, который позволяет получить сеть Петри для представленной на электронной карте в виде условных знаков тактической задачи.
Транслятор состоит из трех основных блоков: лексического анализатора, синтаксического анализатора и генератора сети Петри. В качестве формата хранения сети Петри выбран PNML (Petri Net Markup Language) [9], являющийся разновидностью XML-языка разметки. Транслятор построен по многопроходной схеме взаимодействия бло- ков [10], то есть лексический анализатор полно- стью обрабатывает исходные данные – нанесенное на электронную карту решение оператора, формируя на выходе цепочку лексем. Анализатором осуществляются поиск всех условных тактических знаков, нанесенных на заданную в настройках транслятора электронную карту, считывание их метрик и семантических характеристик, разделение условных тактических знаков на вершины V и дуги A. Затем производится сортировка вершин в порядке возрастания их нумерации. На выходе лексического анализатора формируются два массива: один содержит вершины, другой – дуги. Только после этого управление передается синтаксическому анализатору.
Синтаксический анализатор получает сформированную цепочку лексем и на ее основе формирует промежуточное представление сети Петри. Для этого в синтаксическом анализаторе выполняются следующие действия:
- инициализация дуг путем сравнения координат первой и последней точек метрик тактических знаков, кодирующих групповые действия, с областями метрик рубежей: ai,j,l = (vi, vj), где l – кратность дуги между i-й и j-й вершинами;
- синтаксический разбор лексем, включающий в себя проверку на дублирование нумераций рубежей, корректность введенных оператором семантических характеристик, непротиворечивость количества входных и выходных дуг и т.п.;
- ведение журнала событий процесса трансляции;
- формирование промежуточного представления сети Петри в виде двудольного графа с назначением его элементам экранных координат для последующей визуализации.
Формирование промежуточного представления сети Петри осуществляется в соответствии со следующими правилами:
- до начала выполнения задачи группа только одна, поэтому в сети Петри это условие соответствует начальному состоянию p0;
 - задача разбиения группы на подгруппы представляется макрос-переходом и позициями, количество которых равно количеству исходных рубежей k (рис. 1а), а каждая позиция соответствует условию успешной инициализации подгруппы;
- задача разбиения группы на подгруппы представляется макрос-переходом и позициями, количество которых равно количеству исходных рубежей k (рис. 1а), а каждая позиция соответствует условию успешной инициализации подгруппы;
- каждой подгруппе по умолчанию назначается групповое действие – выход на установленный рубеж;
- каждая дуга ai,j,l (групповое действие) заменяется макрос-переходом и позицией (рис. 1б);
- каждая вершина vi замещается связкой макрос-переходов и позиций (рис. 1г), количество входных дуг в макрос-переход определяется количеством подходящих к рубежу подгрупп и типом рубежа b (0 – исходный рубеж, 1 – рубеж регулирования, 2 – рубеж действия), количество выход- ных позиций – количеством покидающих рубеж подгрупп r;
- аналогично начальному моменту времени этап завершения задачи заменяется макрос-переходом, количество входных дуг которого определяется конечным числом подгрупп (рис. 1в).
Макрос-переход имеет структуру, сходную с описанной в работе [7]. К каждому макрос-переходу осуществляется привязка определенного группового действия. Нумерация позиций и макрос-переходов в пределах одной сети уникальна и задается таким образом, что позволяет однозначно определить их принадлежность к конкретному типу и индексу рубежа или к групповому действию.
Конечный формат представления тактической задачи (PNML) предполагает представление сети Петри в виде перечня объектов, основанное на расширяемом языке разметки XML: узлов (переходов и позиций) и соединяющих их дуг. К объектам привязаны их атрибуты, например, идентификаторы, семантические характеристики (порядок построения, порядок следования, скорость, время и т.п.), а также координаты экранного представления.
Программная реализация транслятора
Традиционный подход к построению трансля- торов предполагает работу исключительно со стро- ковыми данными. При таком подходе было бы необходимо представить данные ГИС в виде последовательности символов, после чего передать полученную последовательность на вход транслятору. Недостатком существующих программных инструментов для автоматической генерации лексических и синтаксических анализаторов, например Lex и Yacc, является то, что сгенерированный таким образом анализатор представляет собой «черный ящик». Альтернативой описанному подходу является построение транслятора на основе объектно-ориентированного подхода, при котором полученная из ГИС информация и средства ее обработки представлены некоторыми классами с необходимым набором полей и методов. В качестве языка программирования для разработки транслятора был выбран язык С++ – кроссплатформенный компилируемый язык с поддержкой объектно-ориентированного подхода.
Набор доступных оператору условных графических обозначений на электронных картах определяется классификатором карты. Для транслятора был разработан специальный классификатор для карт ГИС «Панорама», выполненный по аналогии с классификатором, описанным в работе [11]. Разработанный классификатор включает в себя условные тактические знаки, кодирующие групповые действия НРТК ВН, и семантические характеристики, кодирующие параметры этих действий. Классификатор также содержит идентификаторы объектов карты, обеспечивающие доступ к последним через программный интерфейс приложения ГИС «Панорама».
Для работы транслятора, помимо идентификаторов тактических знаков и семантик, необходимо задать название пользовательской карты, на которой оператор наносит решение тактической задачи, рабочую систему координат, имя и путь к выходному файлу, хранящему описание сети Петри и другие вспомогательные параметры. Учитывая, что разрабатываемый транслятор можно рассматривать как один из видов системы автоматизированного проектирования, оператору предоставлена возможность указания перечисленных параметров. Для этого в начале работы транслятора осуществляются чтение конфигурационного файла настроек и проверка корректности считанных параметров.
 Также были разработаны структуры данных, взаимосвязи между которыми представлены на диаграмме классов (рис. 2). Для хранения считанных с ГИС данных служит класс MapObject (объект карты), имеющий двух наследников: MarkObject (объекты рубежей) и TaskObject (объекты групповых действий).
Также были разработаны структуры данных, взаимосвязи между которыми представлены на диаграмме классов (рис. 2). Для хранения считанных с ГИС данных служит класс MapObject (объект карты), имеющий двух наследников: MarkObject (объекты рубежей) и TaskObject (объекты групповых действий).
Орграф тактической задачи представлен контейнером типа «словарь» (std::map), который позволяет хранить данные в виде пар «ключ–значение». В качестве ключей выступают строковые уникальные идентификаторы позиций и переходов сети Петри (вершин орграфа), значениями явля- ются сами позиции и переходы (класс Node) и указатели на смежные вершины. В классе Node указаны тип вершины, ее идентификатор и указатель на соответствующий объект карты (MapObject). Работу по трансляции реализуют два основных класса – Translator и Wrapper. В классе Translator реализованы необходимые операции лексического, синтаксического, семантического разбора и генерации конечного представления задачи в виде сети Петри. Перечисленные основные фазы работы транслятора разбиты на отдельные шаги, реализованные в методах класса Translator. Класс Wrapper хранит все необходимые для трансляции данные и выполняет запуск методов класса Translator в нужной последовательности, при этом происходит сохранение информации о выполняемых операциях при помощи экземпляра класса Logger. При возникновении на любом шаге трансляции неустранимых ошибок работа транслятора завершается с уведомлением оператора об ошибке.
Поскольку используемый для конечного представления сети Петри формат PNML предполагает графическое представление сети, на одном из этапов работы приложения происходит инициализация координат вершин двудольного графа. Для масштабирования экранного представления сети Петри под указанное пользователем разрешение необходимо определить максимальную длину простого пути (наибольшее число последовательных групповых действий) и количество параллельных путей. Данная операция выполняется при помощи модифицированного метода поиска в ширину. Результатом поиска является объект класса std::multimap> («мультисловарь»), который хранит идентифика- торы вершин с исходящими параллельными дугами и массивы с последовательностью вершин в этих путях. Далее происходит рекурсивное присваивание координат позициям и переходам графа сети Петри, начиная с пути, имеющего максимальную длину.
В конце работы транслятора происходит перевод полученного промежуточного представления сети Петри в формат PNML при помощи специализированной библиотеки. В результате успешного процесса трансляции создается файл с заданным именем, содержащий PNML-описание сети Петри, соответствующей орграфу тактической задачи.
 Транслятор реализован в виде DLL-библиотеки translator.dll, динамически подключаемой к ГИС «Панорама». Запуск транслятора осуществляется через меню «Запуск приложений» ГИС. В качестве примера на рисунке 3а приведен результат работы транслятора для примера тактической задачи (рис. 3б). Здесь по замыслу оператора с исходных рубежей 1 и 2 начинают выполнять движение в колонне три подгруппы: первая, состоящая из одного НРТК ВН № 1 со скоростью 15 км/ч с рубежа 1, вторая – из двух НРТК ВН № 2 и № 3 со скоростью 15 км/ч с рубежа 2, третья – из двух НРТК ВН № 4 и № 5 со скоростью 10 км/ч. Первая и вторая подгруппы объединяются на рубеже регулирования 3 и продолжают движение до встречи и объединения на рубеже 4 с третьей подгруппой.
Транслятор реализован в виде DLL-библиотеки translator.dll, динамически подключаемой к ГИС «Панорама». Запуск транслятора осуществляется через меню «Запуск приложений» ГИС. В качестве примера на рисунке 3а приведен результат работы транслятора для примера тактической задачи (рис. 3б). Здесь по замыслу оператора с исходных рубежей 1 и 2 начинают выполнять движение в колонне три подгруппы: первая, состоящая из одного НРТК ВН № 1 со скоростью 15 км/ч с рубежа 1, вторая – из двух НРТК ВН № 2 и № 3 со скоростью 15 км/ч с рубежа 2, третья – из двух НРТК ВН № 4 и № 5 со скоростью 10 км/ч. Первая и вторая подгруппы объединяются на рубеже регулирования 3 и продолжают движение до встречи и объединения на рубеже 4 с третьей подгруппой.
Из рисунка 3а видно, что вначале группа одна (состояние p0), далее происходят инициализация двух подгрупп и их выход на исходные рубежи (m0), затем инициализация подгрупп перед исходными рубежами (m0|1|1 и m0|2|1), перераспределение НРТК ВН между тремя подгруппами на исходных рубежах (m0|1|2 и m0|2|2), перемещение двух подгрупп к рубежу регулирования (m3|1|3|1 и m3|2|3|1), а третьей – к конечному рубежу (m3|2|4|2). Первые две подгруппы перед рубежом 3 объединяются в одну подгруппу (m1|3|1), производят инициализацию после рубежа (m1|3|2) и в составе объединенной подгруппы совершают движение к конечному рубежу (m3|3|4|1), где объединяются с третьей подгруппой (m2|4|1 и m2|4|2) и завершают выполнение тактической задачи (m5). Cравнение полученной сети Петри (рис. 3б) с композицией элементов, составляющих ее (рис. 1б), подтверждает корректность работы транслятора.
Заключение
Применение разработанного транслятора совместно с ГИС позволило автоматизировать процесс формирования тактической задачи для группы НРТК ВН: во-первых, была достигнута наглядность тактического решения за счет его графического представления на карте, во-вторых, с помощью электронной карты осуществлена привязка решения к местности, в-третьих, получено преобразование решения оператора в эквивалентную сеть Петри. Таким образом, достигнутые результаты делают предложенный в работе [7] подход к формализации тактической задачи пригодным для его практического применения операторами при групповом управлении наземными робототехническими комплексами и позволяют разработчикам групповых алгоритмов не только анализировать последовательность действий групп НРТК ВН, но и наглядно представлять состояние последних в ходе выполнения задачи.
Литература
1. Ветлугин Р., Васильков А. Робототехнические комплексы сухопутных войск США и взгляды военных специалистов на их применение // Зарубежное военное обозрение. 2016. № 6. С. 55–59.
2. Palomeras N., Ridao P., Carreras M. Using Petri nets to specify and execute missions for autonomous underwater vechicles. Proc. IEEE/RSJ Intern. Conf. of Intelligent Robots and Systems, Louis, USA, 2009, pp. 4439–4444. DOI: 10.1109/IROS.2009. 5354045.
3. Remmersmann T., Schade U., Tiderko A. Commanding heterogeneous multi-robot teams. Proc. 19th ICCRTS, Alexandria, the USA, 2014, p. 32. DOI: 10.1007/978-3-319-66471-2_25.
4. Palomeras N., Ridao P., Silvestre C., El-Fakdi A. Multiple vehicles mission coordination using Petri nets. Proc. IEEE Intern. Conf. on Robotics and Automation Convention, Anchorage, Alaska, USA, 2010, pp. 3531–3536. DOI: 10.1109/ROBOT.2010.5509552.
5. Yasuda G. Implementation of distributed control architecture for multiple robot systems using Petri nets: Petri Nets – Manufacturing and Computer Science. InTech Publ., 2012, pp. 75–94. DOI: 10.5772/50577.
6. Jianhong Ye, Zhiwu Li. Decentralized supervision of Petri nets with coordinator. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, vol. 45, iss. 6, pp. 955–966. DOI: 10.1109/TSMC.2013.2244208.
7. Максимов А.А., Тачков А.А., Малыхин А.Ю., Рудиа- нов Н.А. Подход к формализации тактической задачи для группы наземных робототехнических комплексов военного назначения // Вопросы оборонной техники: Сер. 16. 2017. № 7–8. С. 88–96.
8. Демиденко Р.А. Опыт реализации сетецентрической системы управления с использованием ГИС «Оператор» // Геопрофи. 2013. № 1. С. 8–11.
9. PNML reference site. URL: http://www.pnml.org/ (дата обращения: 02.05.2018).
10. Новичкова М.И., Трофимов Ю.А. Разработка транслятора языка программирования высокого уровня // Образование и наука в современных условиях: матер. IV Междунар. науч.-практич. конф. 2015. № 3. С. 213–214.
11. Войцеховский С.В., Девяткин А.М., Котенок А.А., Обухов А.В. Особенности создания пользовательского классификатора для отображения обстановки на электронной карте // Программные продукты и системы. 2014. № 3. С. 44–47. DOI: 10.15827/0236-235X.107.044-047.
References
- Vetlugin R., Vasilkov A. Robotic complexes of the US Army and the views of military specialists on their use. Foreign Military Review. 2016, no. 6, pp. 55–59 (in Russ.).
- Palomeras N., Ridao P., Carreras M. Using Petri nets to specify and execute missions for autonomous underwater vehicles. Proc. IEEE/RSJ Intern. Conf. of Intelligent Robots and Systems. Louis, USA, 2009, pp. 4439–4444. DOI: 10.1109/IROS.2009.5354045.
- Remmersmann T., Schade U., Tiderko A. Commanding heterogeneous multi-robot teams. Proc. 19th Intern. Command and Control Research and Technology Symp. (ICCRTS). 2014, Alexandria, USA, p. 32. DOI: 10.1007/978-3-319-66471-2_25.
- Palomeras N., Ridao P., Silvestre C., El-Fakdi A. Multiple vehicles mission coordination using Petri nets. Proc. IEEE Intern. Conf. on Robotics and Automation Convention. Anchorage, Alaska, USA, 2010, pp. 3531–3536. DOI: 10.1109/ROBOT.2010.5509552.
- Yasuda G. Implementation of distributed control architecture for multiple robot systems using Petri nets. Petri Nets – Manufacturing and Computer Science. InTech Publ., 2012, pp. 75–94. DOI: 10.5772/50577.
- Jianhong Ye, Zhiwu Li. Decentralized supervision of Petri nets with coordinator. IEEE Trans. on Systems, Man, and Cybernetics: Systems. 2015, vol. 45, iss. 6, pp. 955–966. DOI: 10.1109/TSMC.2013.2244208.
- Maksimov A.A., Tachkov A.A., Malykhin A.Yu., Rudianov N.A. An approach to formalization of mission plan for group of military unmanned ground vehicles. Military Enginery. Iss. 16. 2017, no. 7–8, pp. 88–96 (in Russ.).
- Demidenko R.A. Experience in implementing a network-centric control system using GIS Operator. Geoprofi. 2013, no. 1, pp. 8–11 (in Russ.).
- PNML reference site. Available at: http://www.pnml.org/ (accessed May 2, 2018).
- Novichkova M.I., Trofimov Yu.A. Development of a high-level programming language translator. Education and Science in Modern Conditions: Proc. 4th Intern. Sci. and Pract. Conf. 2015, no. 3, pp. 213–214 (in Russ.).
- Voytsekhovsky S.V., Devyatkin A.M., Kotenok A.A., Obukhov A.V. Features of creating a custom classifier to display the situation on an electronic map. Software & Systems. 2014, no. 3, pp. 44–47 (in Russ.). DOI: 10.15827/0236-235X.107.044-047.



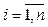 , n = ½V½), а групповое действие aj – дугой (aj Î A,
, n = ½V½), а групповое действие aj – дугой (aj Î A, , m = ½A½). Дуги могут быть кратными: при выполнении одного и того же действия между двумя рубежами несколькими разными подгруппами. Каждый из рубежей имеет свой номер, указываемый в соответствующей семантической характеристике (атрибуте знака в ГИС) и отображаемый на электронной карте. Нумерация начинается с исходных рубежей и для исключения неоднозначности ведется оператором на карте слева направо в направлении действия группы.
, m = ½A½). Дуги могут быть кратными: при выполнении одного и того же действия между двумя рубежами несколькими разными подгруппами. Каждый из рубежей имеет свой номер, указываемый в соответствующей семантической характеристике (атрибуте знака в ГИС) и отображаемый на электронной карте. Нумерация начинается с исходных рубежей и для исключения неоднозначности ведется оператором на карте слева направо в направлении действия группы.


