Прогнозирование временных рядов имеет большое значение во многих прикладных задачах, таких как формирование сигналов на фондовом рынке, управление энергопотреблением, мониторинг центров обработки данных и т.д. Предсказание значений временного ряда часто достаточно затруднительно по причине нестационарности данных. Одним из эффективных и действенных решений этой проблемы является локальная аппроксимация.
В работе рассмотрены кусочно-линейная аппроксимация как, пожалуй, наиболее часто используемый метод обработки данных [1–3], кусочно-логарифмическая аппроксимация, локальные главные компоненты [4, 5] и преобразование Хафа [6]. Для преобразования Хафа предлагается оригинальный алгоритм, учитывающий динамику. В первой модели время входит в качестве аргумента, поэтому параметры модели зависят от временного периода. В остальных моделях время присутствует неявно. Это дает дополнительные преимущества над первой моделью.
Используем следующие обозначения: X – временной ряд, xt – значение временного ряда, t – время. Предполагаем, что время дискретно. Под отрезком временного ряда  , s £ 1, будем понимать последовательность значений
, s £ 1, будем понимать последовательность значений  = {xs, …, xt}.
= {xs, …, xt}.
Сегментация временного ряда. Важным этапом в процессе построения локальных трендов является сегментация временного ряда. Несмотря на то, что существует большое количество методов сегментации, в общем случае их можно сгруппировать в три категории.
1. Скользящее окно: сегмент растет до тех пор, пока не превысит некоторую ошибку e. Процесс повторяется со следующей точки данных, не включенной в недавно полученный сегмент.
2. Сверху вниз: временной ряд рекурсивно разделяют на сегменты до тех пор, пока не будет выполнен некоторый критерий остановки.
3. Снизу вверх: сегменты объединяются, начиная с наилучшей аппроксимации, пока некоторый критерий остановки не будет соблюден.
 Результаты работы методов сегментации для нестационарного временного ряда представлены на рисунке 1. При одном и том же уровне среднеквадратической ошибки, равной 0.5, методы работают по-разному. Методы сверху вниз и скользящее окно аппроксимируют временной ряд достаточно точно, в результате локальные тренды имеют небольшую продолжительность и фактически повторяют ряд. В отличие от них построение локальных трендов с помощью метода снизу вверх позволяет выявить основные направления движения времен- ного ряда, что в процессе построения будущей модели прогнозирования дает большие преимущества. Более подробное описание методов, а также их производительности дано в [7].
Результаты работы методов сегментации для нестационарного временного ряда представлены на рисунке 1. При одном и том же уровне среднеквадратической ошибки, равной 0.5, методы работают по-разному. Методы сверху вниз и скользящее окно аппроксимируют временной ряд достаточно точно, в результате локальные тренды имеют небольшую продолжительность и фактически повторяют ряд. В отличие от них построение локальных трендов с помощью метода снизу вверх позволяет выявить основные направления движения времен- ного ряда, что в процессе построения будущей модели прогнозирования дает большие преимущества. Более подробное описание методов, а также их производительности дано в [7].
Далее для демонстрации работы методов выделения локальных тенденций будем использовать сегментацию снизу вверх с фиксированным количеством сегментов (25). Такой критерий не является оптимальным для сегментации, но позволит сравнить методы выделения локальных тенденций и определить их особенности. В качестве исходных данных будем использовать два набора: данные c электрокардиограммы со сложной периодично- стью (A) и цены закрытий акций Газпрома (B) c таймфреймом в один день.
Кусочно-линейная аппроксимация отрезка  – это приблизительное представление отрезка кусочно-линейной функцией f(t) = ait + bi, t Î [ti–1, ti), s = t0 < t1 < … < tk = t, f(t) = akt + bk.
– это приблизительное представление отрезка кусочно-линейной функцией f(t) = ait + bi, t Î [ti–1, ti), s = t0 < t1 < … < tk = t, f(t) = akt + bk.
Рассмотрим отрезок  = {f(s), …, f(t)}. Качество представления определяется в результате сравнения отрезков
= {f(s), …, f(t)}. Качество представления определяется в результате сравнения отрезков  и
и  . Один из наиболее популярных критериев – среднее квадратическое отклонение:
. Один из наиболее популярных критериев – среднее квадратическое отклонение:
 . (1)
. (1)
 Другим критерием качества аппроксимации является число точек разбиения k + 1. Задача построения кусочно-линейной аппроксимации заключается в одновременной минимизации каждого из этих критериев (рис. 2). К сожалению, при построении аппроксимации можно использовать только доступную информацию, настоящее и прошлое, то есть нельзя заглядывать в будущее. С учетом по- следнего в текущий момент времени необходимо определять, присоединять текущее значение временного ряда xr к совокупности или формировать новую совокупность. Для приемлемого решения задачи кусочно-линейной аппроксимации предлагается итерационный алгоритм, который подробно будет описан далее на примере кусочно-логарифмической модели. Кусочно-линейная аппроксимация как средство предобработки данных рассмотрена в ряде работ, например в [8, 9].
Другим критерием качества аппроксимации является число точек разбиения k + 1. Задача построения кусочно-линейной аппроксимации заключается в одновременной минимизации каждого из этих критериев (рис. 2). К сожалению, при построении аппроксимации можно использовать только доступную информацию, настоящее и прошлое, то есть нельзя заглядывать в будущее. С учетом по- следнего в текущий момент времени необходимо определять, присоединять текущее значение временного ряда xr к совокупности или формировать новую совокупность. Для приемлемого решения задачи кусочно-линейной аппроксимации предлагается итерационный алгоритм, который подробно будет описан далее на примере кусочно-логарифмической модели. Кусочно-линейная аппроксимация как средство предобработки данных рассмотрена в ряде работ, например в [8, 9].
Кусочно-логарифмическая аппроксимация. Используем обозначения предыдущего раздела. Кусочно-логарифмическая аппроксимация отрезка  – это приблизительное представление отрезка
– это приблизительное представление отрезка  отрезком
отрезком  : yt+1 = aixt, t Î [ti–1, ti), s = t0 < < t1 < … < tk = t. В данной модели критерий, аналогичный критерию (1), имеет следующий вид:
: yt+1 = aixt, t Î [ti–1, ti), s = t0 < < t1 < … < tk = t. В данной модели критерий, аналогичный критерию (1), имеет следующий вид:
 . (2)
. (2)
Критерий (2) в отличие от критерия (1) позволяет получить статистику, инвариантную по отношению к масштабу, что позволяет избавиться от ряда проблем при обучении (рис. 3).
Локальные главные компоненты. В этой модели рассмотрим отрезок  ={(Dxs+1, xs), …, (Dxt, xt–1)} как множество случайных точек на плоскости. Как и раньше, разбиение s = t0 < t1 < < … < tk = t. Отрезок
={(Dxs+1, xs), …, (Dxt, xt–1)} как множество случайных точек на плоскости. Как и раньше, разбиение s = t0 < t1 < < … < tk = t. Отрезок  , где
, где  . Обозначим через
. Обозначим через  выборочную ковариационную матрицу, соответствующую множеству
выборочную ковариационную матрицу, соответствующую множеству 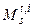 , ее собственные числа
, ее собственные числа  Критерий для данной модели будет иметь вид:
Критерий для данной модели будет иметь вид:
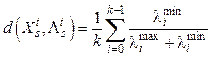 , (3)
, (3)
где  . Критерий (3) инвариантен и к сдвигу, и к масштабу. Локальные главные компоненты (рис. 4) также рассматривались в ряде работ, например в [4, 5].
. Критерий (3) инвариантен и к сдвигу, и к масштабу. Локальные главные компоненты (рис. 4) также рассматривались в ряде работ, например в [4, 5].
 Алгоритм. Как уже отмечалось, качество локальной аппроксимации определяется критериями d и k. Данную задачу будем рассматривать в следующей постановке. Первый критерий ограничим: d £ e, второй критерий постараемся сделать как можно меньшим.
Алгоритм. Как уже отмечалось, качество локальной аппроксимации определяется критериями d и k. Данную задачу будем рассматривать в следующей постановке. Первый критерий ограничим: d £ e, второй критерий постараемся сделать как можно меньшим.
Общий для всех методов алгоритм будет выглядеть следующим образом.
1. Формирование начальной выборки. Если выборка исчерпана, то переход к п. 5.
2. Добавление нового элемента. Если выборка исчерпана, то переход к п. 5.
3. Если новый элемент добавлен, то вычисление параметров модели и переход к п. 2.
4. Переход к п. 1.
5. Остановка.
Рассмотрим подробнее алгоритм на примере второй модели. Начальная выборка должна содержать два элемента, вычисляются показатели  и значение теста T1 = 0. Добавление элемента. Пусть после n итераций сформирована выборка со значениями
и значение теста T1 = 0. Добавление элемента. Пусть после n итераций сформирована выборка со значениями  и Mn. Рассматривается возможность добавления к выборке элемента xn+1. Для этого вычисляются новые значения показателей
и Mn. Рассматривается возможность добавления к выборке элемента xn+1. Для этого вычисляются новые значения показателей 
 и значение теста
и значение теста  . Элемент добавляется к выборке, если справедливо неравенство Tn+1 £ e. Если неравенство не выполняется, определяются наклон a = Mn и длина локального отрезка l = n.
. Элемент добавляется к выборке, если справедливо неравенство Tn+1 £ e. Если неравенство не выполняется, определяются наклон a = Mn и длина локального отрезка l = n.
Преобразование Хафа. Данный метод широко используется при анализе изображений [6]. Как и в модели локальной главной компоненты, рассмотрим множество точек на плоскости  ={(Dxs+1, xs), …, (Dxt, xt–1)}. Преобразование Хафа отображает каждую точку
={(Dxs+1, xs), …, (Dxt, xt–1)}. Преобразование Хафа отображает каждую точку  в синусоиду на параметрической плоскости (j, r) с помощью равенства
в синусоиду на параметрической плоскости (j, r) с помощью равенства
r = u cosj + v sinj. (4)
В параметрической плоскости строится сетка с узлами:
ci,j = (ji, rj) = (iDj, jDr), i = –l, –l + 1, …, 0, …, l; j = 0, 1, … Причем lDj = 2p. Вычисляется матрица H. Первоначально все элементы матрицы равны нулю, затем каждый элемент  изменяет матрицу H следующим образом:
изменяет матрицу H следующим образом:  ; i = –l, –l + 1, …, 0, …, l; ji = max{j: rj £ u cosji + + v sinji}. Определяется множество локальных максимумов LH = {(ik, jk)} матрицы H, по которому определяются параметры отрезков прямых
; i = –l, –l + 1, …, 0, …, l; ji = max{j: rj £ u cosji + + v sinji}. Определяется множество локальных максимумов LH = {(ik, jk)} матрицы H, по которому определяются параметры отрезков прямых  , аппроксимирующих множество точек
, аппроксимирующих множество точек  , k = 1, …, m. Множество отрезков прямых разбивает множество на непересекающиеся подмножества
, k = 1, …, m. Множество отрезков прямых разбивает множество на непересекающиеся подмножества 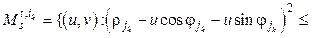

 Если разбиение множества
Если разбиение множества  соответствует динамике, полученный набор прямых является кусочно-линейной аппроксимацией.
соответствует динамике, полученный набор прямых является кусочно-линейной аппроксимацией.
Динамическое преобразование Хафа. Классическое применение преобразования Хафа имеет один недостаток. Этот метод кластеризации работает со сформированной обучающей выборкой, что накладывает ограничения при его использовании в online-обучении. Рассмотрим метод, учитывающий динамику выборки в контексте приведенного выше алгоритма. Начальная выборка содержит два элемента: (u1, v1) и (u2, v2). С использованием (4) вычисляются (j1, r1). Сначала вычисляется угол
 , (5)
, (5)
если ½v1, v2½ > e. Затем вычисляются
ra = u1 cosja + v1 sinja и
 (6)
(6)
Если ½v1 – v2½ £ e, то
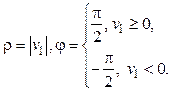 (7)
(7)
Пусть сформирована выборка из n элементов с (jn, rn) и решается вопрос о добавлении следующего элемента (un+1, vn+1) (un+1 = Dxn+1, vn+1 = xn). Для этого вычисляются приращения:
 , (8)
, (8)
где A = un+1 cosjn + vn+1 sinjn, B = vn+1 cosjn – – un+1sinjn. Вычисляется тест
 . (9)
. (9)
Если T £ e, то (un+1, vn+1) добавляется к выборке и вычисляется
 , (10)
, (10)
иначе (un+1, vn+1) не добавляется к выборке и определяются l = n и угол наклона отрезка  .
.
Прогнозирование с помощью локальной аппроксимации. Применение локальной аппрокси- мации возможно двумя способами. Первый способ заключается в том, что перед вычислением прогноза временного ряда вычисляются параметры локальной аппроксимации с использованием исторических данных.
Рассмотрим это на примере кусочно-логарифмической модели. Вычисляется точка (a, t) с использованием последовательности точек (ai, ti). Параметр a определен ранее, а параметр t – длина локальной аппроксимации. По сути t – это число использований модели с параметром a перед пересчетом (a, t). Прогноз вычисляется по простой формуле: yt+1 = xt (1 + a). Вычислить точку (a, t) можно на нейронной сети сложной архитектуры, например CNN и LSTM, с эффективным алгоритмом обучения [10].
Второй способ – это прогноз с одновременным вычислением локального тренда. Рассмотрим соответствующий алгоритм с использованием динамического преобразования Хафа.
Пусть текущее значение дискретного времени t. Определим точность e и регуляризующий пара- метр a.
1. Полагаем n = t – 3. Если выборка исчерпана, то переход к п. 5. Вычисляется (j, r) с использованием формул (5) и (6) или (7) и двух точек с координатами u2 = xt – xt–1, v2 = xt–1, u1 = xt–1 – xt–2, v1 = xt–2.
2. k = 2.
3. Добавление новой точки с координатами u = xn+1 – xn, v = xn. Если выборка исчерпана, то переход к п. 4. С использованием формулы (8) вычисляются Dj, Dr и T:
 ,
,
где A = u cosj + v sinj, B = v cosj – u sinj,  .
.
Если T > e, то переход к п. 4.
Вычисляются с применением (9):  и
и 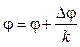 , а также n: = n – 1 и k = k+ 1.
, а также n: = n – 1 и k = k+ 1.
Переход к п. 3.
4. Вычисляются прогноз
 и новое значение для t = t + 1. Переход к п. 1.
и новое значение для t = t + 1. Переход к п. 1.
5. Остановка.
Проведем два эксперимента с наборами данных A и B. Результаты прогноза на наборе A приведены на рисунке 5.
Второй эксперимент – это прогноз на наборе данных B. Результат показан на рисунке 6.

Заключение
В данной работе основное внимание уделяется изучению локальных тенденций во временных ря- дах. Предполагается, что такая последовательность тенденций описывает долгосрочную взаимосвязь во временном ряду и, таким образом, естественно влияет на изменение следующего локального тренда. Применение методов выделения тенденций совместно с применением нейросетевых методов может значительно улучшить результаты прогнозирования.
В работе также рассмотрена неблагодарная задача прогноза. За основу взята идея кусочно- линейной аппроксимации и предложен алгоритм прогноза с использованием динамического преобразования Хафа. Отметим, что алгоритм легко распространяется на остальные способы кусочно-линейной аппроксимации данных. Данные экспериментов показали применимость предложенного метода для прогнозирования временного ряда. По крайней мере, тенденции воспроизводятся и в первом, и во втором экспериментах. Дальнейшего улучшения результатов следует ожидать при одновременном прогнозе тренда, его продолжительности и значений временного ряда.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-01-00888 а.
Литература
1. Hunter J., McIntosh N. Knowledge-based event detection in complex time series data. Artificial Intelligence in Medicine. Springer. 1999, pp. 271–280.
2. Ge X., Smyth P. Segmental Semi-Markov models for endpoint detection in plasma etching. IEEE Transactions on Semiconductor Eng., 2001, vol. 259, pp. 201–209.
3. Wang Peng, Wang Haixun, and Wang Wei. Finding semantics in time series. Proc. 2011 ACM SIGMOD Intern. Conf. on Management of Data, 2011, pp. 385–396.
4. Belyavsky G., Puchkov E. Nonlinear principal component analysis approach to pattern recognition // Modeling of Artificial Intelligence, 2016, vol. 9, iss. 1, pp. 24–32.
5. Golyandina N., Nekrutkin V., and Zhigljavsky A. Analysis of time series structure: SSA and related techniques. Chapman & Hall/CRC, 2001, 320 p.
6. Canny J.F. A computational approach to edge detection. IEEE Trans. Pattern Analysis and Machine Intelligence, 1986, no. 8, pp. 679–698.
7. Keogh E., Chu S., Hart D., Pazzani M. Segmenting time series: A survey and novel approach, in: Data mining in time series databases, World Scientific, Singapore, 2004, pp. 1–21.
8. Keogh E, Chakrabarti K., Pazzani M. & Mehrotra S. Dimensionality reduction for fast similarity search in large time series databases. Knowledge and Information Systems, 2000, no. 3, pp. 263–286.
9. Matsubara Ya., Sakurai Ya., and Faloutsos Ch. AutoPlait: Automatic mining of coevolving time sequences. Proc. 2014 ACM SIGMOD Intern. Conf. on Management of Data, 2014, pp. 193–204. DOI: 10.1145/2588555.2588556.
10. Lin Tao, Guo Tian, Aberer K. Hybrid neural networks for learning the trend in time series. Proc. 26th Intern. Joint Conf. on Artificial Intelligence, 2017, pp. 2273–2279.
References
- Hunter J., McIntosh N. Knowledge-based event detection in complex time series data. Artificial Intelligence in Medicine. Springer Publ., 1999, pp. 271–280.
- Ge X., Smyth P. Segmental Semi-markov models for endpoint detection in plasma etching. IEEE Trans. on Semiconductor Eng. 2001, vol. 259, pp. 201–209.
- Wang Peng, Wang Haixun, Wang Wei. Finding semantics in time series. Proc. 2011 ACM SIGMOD Intern. Conf. on Management of Data. 2011, pp. 385–396.
- Belyavsky G., Puchkov E. Nonlinear principal component analysis approach to pattern recognition. Modeling of Artificial Intelligence. 2016, vol. 9, iss. 1, pp. 24–32.
- Golyandina N., Nekrutkin V., Zhigljavsky A. Analysis of time series structure: SSA and related techniques. Chapman & Hall/CRC Publ., 2001, 320 p.
- Canny J.F. A computational approach to edge detection. IEEE Trans. Pattern Analysis and Machine Intelligence. 1986, no. 8, pp. 679–698.
- Keogh E., Chu S., Hart D., Pazzani M. Segmenting time series: A survey and novel approach. Data mining in time series databases. World Scientific, Singapore, 2004, pp. 1–21.
- Keogh E., Chakrabarti K., Pazzani M., Mehrotra S. Dimensionality reduction for fast similarity search in large time series databases. Knowledge and Information Systems. 2000, no. 3, pp. 263–286.
- Matsubara Ya., Sakurai Ya., Faloutsos Ch. AutoPlait: Automatic mining of coevolving time sequences. Proc. 2014 ACM SIGMOD Intern. Conf. on Management of Data. 2014, pp. 193–204. DOI: 10.1145/2588555.2588556.
- Lin Tao, Guo Tian, Aberer K. Hybrid neural networks for learning the trend in time series. Proc. 26th Intern. Joint Conf. on Artificial Intelligence. 2017, pp. 2273–2279.



 , s £ 1, будем понимать последовательность значений
, s £ 1, будем понимать последовательность значений 
 = {f(s), …, f(t)}. Качество представления определяется в результате сравнения отрезков
= {f(s), …, f(t)}. Качество представления определяется в результате сравнения отрезков  . (1)
. (1)
 : yt+1 = aixt, t Î [ti–1, ti), s = t0 < < t1 < … < tk = t. В данной модели критерий, аналогичный критерию (1), имеет следующий вид:
: yt+1 = aixt, t Î [ti–1, ti), s = t0 < < t1 < … < tk = t. В данной модели критерий, аналогичный критерию (1), имеет следующий вид: . (2)
. (2) ={(Dxs+1, xs), …, (Dxt, xt–1)} как множество случайных точек на плоскости. Как и раньше, разбиение s = t0 < t1 < < … < tk = t. Отрезок
={(Dxs+1, xs), …, (Dxt, xt–1)} как множество случайных точек на плоскости. Как и раньше, разбиение s = t0 < t1 < < … < tk = t. Отрезок  , где
, где  . Обозначим через
. Обозначим через  выборочную ковариационную матрицу, соответствующую множеству
выборочную ковариационную матрицу, соответствующую множеству 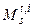 , ее собственные числа
, ее собственные числа  Критерий для данной модели будет иметь вид:
Критерий для данной модели будет иметь вид: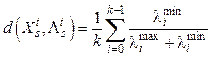 , (3)
, (3) . Критерий (3) инвариантен и к сдвигу, и к масштабу. Локальные главные компоненты (рис. 4) также рассматривались в ряде работ, например в [4, 5].
. Критерий (3) инвариантен и к сдвигу, и к масштабу. Локальные главные компоненты (рис. 4) также рассматривались в ряде работ, например в [4, 5].
 и значение теста T1 = 0. Добавление элемента. Пусть после n итераций сформирована выборка со значениями
и значение теста T1 = 0. Добавление элемента. Пусть после n итераций сформирована выборка со значениями  и Mn. Рассматривается возможность добавления к выборке элемента xn+1. Для этого вычисляются новые значения показателей
и Mn. Рассматривается возможность добавления к выборке элемента xn+1. Для этого вычисляются новые значения показателей 
 и значение теста
и значение теста  . Элемент добавляется к выборке, если справедливо неравенство Tn+1 £ e. Если неравенство не выполняется, определяются наклон a = Mn и длина локального отрезка l = n.
. Элемент добавляется к выборке, если справедливо неравенство Tn+1 £ e. Если неравенство не выполняется, определяются наклон a = Mn и длина локального отрезка l = n. в синусоиду на параметрической плоскости (j, r) с помощью равенства
в синусоиду на параметрической плоскости (j, r) с помощью равенства ; i = –l, –l + 1, …, 0, …, l; ji = max{j: rj £ u cosji + + v sinji}. Определяется множество локальных максимумов LH = {(ik, jk)} матрицы H, по которому определяются параметры отрезков прямых
; i = –l, –l + 1, …, 0, …, l; ji = max{j: rj £ u cosji + + v sinji}. Определяется множество локальных максимумов LH = {(ik, jk)} матрицы H, по которому определяются параметры отрезков прямых  , аппроксимирующих множество точек
, аппроксимирующих множество точек 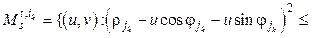


 , (5)
, (5) (6)
(6)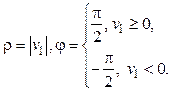 (7)
(7) , (8)
, (8) . (9)
. (9) , (10)
, (10) .
. .
. и
и 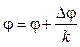 , а также n: = n – 1 и k = k+ 1.
, а также n: = n – 1 и k = k+ 1. и новое значение для t = t + 1. Переход к п. 1.
и новое значение для t = t + 1. Переход к п. 1.
