Модели и алгоритмы вычисления топологических отношений в геоинформационных системах
| Андрианов Д.Е. () - , Булаев А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Современные геоинфомационные технологии находят применение в самых различных сферах деятельности человека. Особенно интенсивно геоинформационные системы (ГИС) внедряются в системы управления городскими службами, начиная от создания земельного кадастра и заканчивая телекоммуникационными системами управления энергетическим обеспечением. В современных условиях любому городу для эффективного развития необходимы инвестиции, которые можно привлечь при условии полной прозрачности управления территорией и коммуникациями.
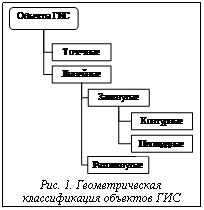
Интегрированные технологии описания и анализа топологических отношений в ГИС позволяют совместно решать ряд проблем, наиболее важными из которых являются: - унифицированность хранения и анализа данных на основе топологических отношений как в двухмерном, так и в трехмерном пространстве; - хранение единого набора отношений вместо отдельных данных для каждого масштаба, что позволяет экономить ресурсы и не сталкиваться с различием отношений для одной и той же территории; - сохранение топологической корректности при генерализации отображаемых объектов; - обеспечение набором необходимых данных алгоритмов вычислений различных параметров объектов [1]. Классификация объектов ГИС С точки зрения геометрии различают 4 вида объектов: точка, линия, полигон, поверхность. Объект «поверхность» присущ работе в трехмерном пространстве. Так как в настоящее время большинство ГИС представляют собой программные средства по работе с 2d-пространствами (картами и планами), то дальнейшее рассмотрение 3d-объектов – отдельное и серьезное направление исследований. В данной работе мы будем рассматривать следующие виды объектов: точечные, полилинейные и полигональные. В общем случае все объекты ГИС могут быть разделены на две большие группы: точечные и линейные. При этом линейные объекты воспринимаются не только как совокупность прямолинейных отрезков, а как объекты, имеющие в своем составе сегменты линий второго и высших порядков. Линейные объекты могут представляться как замкнутыми, так и разомкнутыми совокупностями линейных сегментов. Если принять во внимание, что все объекты ГИС имеют семантический контекст, который определяет их как объекты реального мира, то замкнутые линейные объекты можно подразделить на контурные и площадные объекты. Контурные объекты включают множество точек, принадлежащих непосредственно линии, образующей объект. Площадные объекты представляются множеством точек пространства, принадлежащих как границе, так и внутренней области объекта. Таким образом, классификация объектов ГИС (по геометрическим параметрам) может быть сведена к схеме, изображенной на рисунке 1. При рассмотрении картографических объектов как объектов реального мира нельзя пользоваться лишь их геометрической составляющей, так как она не позволяет понять сущность представляемого на карте объекта. В действительности указанного эффекта можно добиться лишь в пространственной (трехмерной) ГИС. В 2d ГИС воспринять объекты в их реалиях позволяет использование их семантического контекста. Если учесть совокупность геометрического и семантического контекстов объектов, то классификация объектов будет представлена схемой, изображенной на рисунке 2. Взаимное соответствие элементов этих двух классификаций представлено в таблице. Таблица
Классификация топологических отношений Можно выделить три класса топологических отношений (внутренние, межобъектные и концептуальные). Каждый класс определяет большую группу топологических отношений, которые отражают элементы внутренней или внешней топологии. Указанные классы могут перекрываться, взаимодополнять друг друга. В ГИС необходимо найти сбалансированную схему порядка установления топологических отношений. По важности установления указанные выше классы могут рассматриваться в следующем порядке: 1) внутренние – определяют целостность объекта как совокупности элементарных геометрических частей и семантического контекста; 2) концептуальные – топологические отношения, устанавливающие наиболее общие правила расположения объектов, относящихся к разным классам [3]; 3) межобъектные – топологические отношения, устанавливаемые между парой объектов [4]. Установление топологических отношений базируется на геометрическом расположении объектов на карте. Существуют следующие варианты геометрического расположения: касание, пересечение, включение, изолированность. Указанные варианты геометрического расположения могут быть дополнены двумя числовыми характеристиками, которые, на наш взгляд, являются наиболее важными при определении взаимного расположения объектов – расстояние (величина, характеризующая степень удаленности двух объектов, выраженную в единицах измерения, принятых в рассматриваемой системе) и относительное расположение, или угол между характеризующими объект элементами. Примем следующие допущения: в ГИС могут реализовываться простые и сложные топологические отношения; простые топологические отношения подразделяются на виды и типы. Разделение топологических отношений на виды будем производить по комбинации объектов, участвующих в топологическом отношении. Типизацию топологических отношений будем производить по вариантам геометрического расположения и числовым характеристикам. На основании сказанного выделим типы топологических отношений: изолированность, пересечение, вложенность, соседство, близость, удаленность, относительное расположение [5]. Формальное представление объектов в ГИС Объекты в ГИС представляются совокупностью геометрического и семантического контекстов. Примем в качестве модели представления объектов в ГИС модель из работы [6]. Объект в ГИС в общем случае можно описать вектором:
где I – идентификатор объекта; P – геометрическая составляющая объекта; A1, A2, … , AN – семантические атрибуты; N – количество атрибутов объекта. Атрибут Р – содержит не простой тип данных, а некую структуру, которая описывает: положение объекта в пространстве; условные обозначения, которыми отображается объект; другие пространственные особенности и характеристики объектов. Таким образом, параметр P представляется вектором P=(Fi), (2) где i=1..К – порядковый номер формы; N – количество форм в объекте, которому принадлежит компонент P. Каждый элемент данного множества представляет собой описание одной формы и тоже является вектором Fi=(fij), (3) где fij – j-я команда в i-й форме. Формы могут содержать точки, прямые линии и дуги. Таким образом, команды можно разбить на типы. Пусть C – множество команд, с помощью которых возможно указание действия для получения следующей точки в контуре некоторой формы объекта. Множество команд С состоит из C={NULL,M,L,A,CL,CA}, (4) где NULL – пустая команда без параметров; (Move to) – перемещение текущей точки построения объекта в точку, указываемую параметрами команды (x,y); L (Line to) – указывает на наличие в объекте прямой линии от текущей точки построения до точки (x,y), заданной в параметрах команды; (Arc to) – указывает на наличие в объекте дуги от текущей точки построения до точки (x,y), заданной в параметрах, с кривизной c, так же данной в параметре команды; CL (Close by Line) – указывает на то, что объект замкнут прямой линией, которая должна проходить от текущей точки построения до первой точки фигуры; CA (Close by Arc) – указывает на то, что объект замкнут дугой, которая должна проходить от текущей точки построения до первой точки фигуры с кривизной с, заданной в параметрах команды. Поскольку параметры команд в общем случае имеют одинаковый тип данных, вещественное число с плавающей точкой двойной точности, а число параметров в общем случае не превышает 3, отдельную команду fij в (3) представим в виде четверки , (5) где kÎC – тип команды; x,y – координаты точки, смысл которых ясен из типа команды kÎ{M,L,A}; с – кривизна дуги, если kÎ{A,CA}. Данная структура может быть дополнена еще одним общим параметром, который будет характеризовать топологию объекта, то есть структура (0а) примет вид:
где Т – топология объекта, представляющая комбинацию трех элементов, соответствующих классам топологических отношений:
где Internal – внутренняя топология; Inter – межобъектная топология; Conceptual – концептуальная топология. Алгоритмы установления топологических отношений должны базироваться на представленной формальной модели объекта. Любой точечный объект характеризуется координатами расположения.
При рассмотрении отношений между двумя точечными объектами целесообразно говорить об их совпадении и определении расстояния между ними. Рассмотрим два точечных объекта: А(ха,уа), В(xb, yb). Расстояние между точечными объектами определяется корнем суммы квадратов разностей соответствующих координат точных объектов:
Линейный объект характеризуется совокупностью вершин, рассматриваемых в определенной последовательности.
Дальнейшие модели и алгоритмы будут относиться к объектам, состоящим из прямолинейных сегментов. Примем, что линейные объекты в структуре данных представляются с учетом их контекста. Так, например, объекты, выражаемые линией на мелкомасштабной карте, могут выражаться полигоном на крупномасштабной. В пространственной базе данных будет храниться именно крупномасштабное представление, а переход к различным вариантам отображения на мелкомасштабной карте будет производиться с помощью алгоритмов генерализации. Данное допущение возможно, так как в муниципальных ГИС осуществляется работа именно с крупномасштабными отображениями. Таким образом, под линейными подразумеваются объекты, представляемые линией на карте крупного масштаба, рассматриваемые алгоритмы применимы и как части алгоритмов при работе с полигонами для решения задач установления принадлежности точечного объекта границе полигона. Точечные и линейные объекты могут находиться в двух отношениях: включение, то есть линейный объект включает в себя точечный объект, и изолированность. Если точечный и линейный объекты находятся в отношении изолированности, то для характеристики их расположения можно использовать расстояние. Для установления включения точечного объекта в линейный необходимо последовательно рассмотреть каждый сегмент линейного объекта и определить, является ли точечный объект частью рассматриваемого линейного сегмента. Рассмотрим часть линейного объекта а, представленную на рисунке 3, и два точечных объекта Р1 и Р2. Рассмотрим линейный сегмент АВ линейного объекта а. Указанный линейный сегмент является частью прямой b. Так как указанная прямая проходит через точки А и В с известными координатами, то удобно воспользоваться уравнением прямой, проходящей через две заданные точки. Это уравнение имеет следующий вид:
где (хР, уР) – координаты точки, принадлежащей данной прямой. Таким образом, принадлежность точки линии может быть установлена из выполнения равенства (11) при подстановке в него вместо хр и ур соответствующих координат точки. На рисунке 3 точки Р1 и Р2 принадлежат линии b. При этом линейному сегменту принадлежит только точка Р1. Соответственно, помимо проверки принадлежности точки прямой, необходимо производить проверку принадлежности точки линейному сегменту. Это можно выполнить по соотношению:
где (хР, уР) – координаты проверяемой точки. Таким образом, алгоритм установления отношения включения сведется к последовательности шагов: 1) дан вектор L={l1,l2,…,lk-1}={(p1,p2),(p2,p3),…, (pk-1,pk)}, хранящий линейные сегменты, составляющие его контур; 2) итеративно рассматривая сегменты l1, l2, … lm (где m=1,2,…,k-1) линейного объекта, выполнить: 2.1) выбрать пары вершин (pm, pm+1), где m – номер линейного сегмента в объекте; pm, pm+1 – вершины линейного объекта (граничные точки m-го линейного сегмента); 2.2) по формуле (11) определить принадлежность точечного объекта линии b, содержащей линейный сегмент lm, при A=pm, B=pm+1; 2.3) при выполнении (11) проверить принадлежность точечного объекта линейному сегменту по системе (12), в противном случае перейти к 2.5; 2.4) при выполнении системы (12) перейти к 3, в противном случае перейти к 2.5; 2.5) увеличить m на единицу и перейти к 2.1; 3) завершить работу алгоритма. Расстоянием между точечным и линейным объектом будем считать минимальное из расстояний от точечного объекта до сегментов линейного объекта. При рассмотрении расстояния возможны две ситуации: точечный объект проецируется на любой из сегментов линейного объекта, точечный объект не проецируется ни на один сегмент. В случае рассмотрения точечного и линейного объектов необходимо: 1) установить, принадлежит ли проекция точечного объекта линейному сегменту; 2) если точечный объект проецируется на один линейный сегмент, то определяем длину высоты, опущенной из точечного объекта на линейный сегмент; 3) Рассмотрим треугольник АР1В (рис. 4), в нем точка Р1 проецируется на ребро АВ. Для установления этого факта необходимо, чтобы выполнялось условие: то есть углы α и β – острые. В контексте обозначений (рис. 4) выражения для определения величин углов α и β будут выглядеть следующим образом:
При этом равенство знаменателя нулю в любом из выражений (14) будет указывать на совпадение рассматриваемой точки с соответствующей граничной точкой линейного сегмента. Тогда расстояние h1 от точечного объекта до линейного сегмента будет определяться по любой из формул:
Если один из рассмотренных углов будет иметь величину свыше 90°, тогда проекция точки не будет принадлежать линейному сегменту. В этом случае расстояние от точечного объекта до линейного сегмента будет определяться как наименьшее из расстояний до граничных точек линейного сегмента:
Возможна ситуация, когда при наличии сегмента линейного объекта, которому принадлежит проекция точечного объекта, расстояние до линейного объекта будет определяться не длиной перпендикуляра, опущенного из точечного объекта к линейному сегменту, а расстоянием до одной из вершин. Алгоритм определения расстояния между точечным и линейным объектом сводится к выполнению следующих шагов: 1) формируется вектор расстояний от точечного объекта до вершин линейного объекта 2) формируется вектор расстояний от точечного объекта до сегментов линейного объекта 3) расстоянием от точечного объекта до линейного объекта будем считать минимальное из расстояний этих векторов, то есть 4) в случае когда точка лежит на сегменте или совпадает с одной из вершин линейного объекта, расстояние будет приниматься равным 0. Если рассматриваемый линейный объект является замкнутым, то отношение включение меняет свой смысл. Если в случае разомкнутого линейного объекта включение подразумевало установление принадлежности точечного объекта одному из сегментов, то включение в замкнутый линейный объект подразумевает рассмотрение случая, когда точечный объект принадлежит внутренней области замкнутого контура. Для этого воспользуемся методом трассировки луча [7]. Суть метода (рис. 5) состоит в том, что из рассматриваемой точки в пространстве (точечного объекта) пускается луч в произвольном направлении и подсчитывается количество пересечений указанного луча с сегментами линейного объекта. Если количество пересечений нечетно (рис. 5а), то точечный объект принадлежит внутренней области замкнутого линейного объекта, в противном случае (рис. 5б) (количество пересечений четно) точечный объект располагается вне замкнутого линейного объекта. При реализации данного алгоритма необходимо определять точки пересечения луча, пущенного из рассматриваемого точечного объекта, и ребер полигонального объекта. В данном методе может использоваться произвольный луч, но для простоты выберем правый луч. Луч, пущенный из данной точки с координатами (х, у), лежит на прямой, определяемой уравнением:
где f(x,y) – уравнение прямой. Линейные сегменты полигонального объекта задаются координатами граничных точек (Рm(хm, уm), Рm+1(хm+1, уm+1)). Исходя из координат этих точек и в соответствии с выражением (21) определяем угловой коэффициент прямой, включающей линейный сегмент. Подставив значение коэффициента k и координаты одной из граничных точек линейного сегмента в выражение расчета кривизны, определим значение коэффициента смещения:
После определения точки пересечения луча и прямой, содержащей линейный сегмент, необходимо проверить, чтобы полученная точка принадлежала линейному сегменту, а не его продолжению (выражение 12), и чтобы координата абсцисс полученной точки была больше координаты абсцисс проверяемой точки. Перед выполнением указанных действий имеет смысл проверить принципиальную возможность пересечения луча и линейного сегмента. Это можно сделать путем проверки попадания ординаты проверяемой точки в интервал ординат граничных точек линейного сегмента:
где уb, уe – ординаты граничных точек линейного сегмента. Алгоритм установления принадлежности точечного объекта внутренней области линейного замкнутого объекта будет состоять из следующих шагов: 1) 2) ввести переменную-счетчик Intersection, хранящую число пересечений луча и сегментов объекта (в начале работы алгоритма Intersection=0); 3) итеративно рассматривая сегменты l1, l2, … lm (где m=1,2,…,k-1) линейного объекта, выполнить: 3.1) выбрать пару вершин (pm, pm+1), где m – номер линейного сегмента в объекте; pm, pm+1 – вершины линейного объекта (граничные точки m-го линейного сегмента); 3.2) по выражению (20) проверяется возможность пересечения луча с сегментом объекта; 3.3) при выполнении (20) перейти к пункту 3.4, в противном случае перейти к 3.7; 3.4) по выражению (19) найти (xp, yp) – координаты пересечения сегмента и луча; 3.5) после определения (xp, yp) устанавливать расположение найденной точки относительно точечного объекта (по формуле 19):
3.6) при выполнении условия (21) значение Intersection увеличивается на 1; 3.7) увеличить m на единицу и перейти к 3.1; 4) выполнить проверку на четность Intersection: в случае четности точечный объект не принадлежит внутренней области линейного объекта, в противном случае – принадлежит; 5) завершение работы алгоритма. Для нахождения пересечения линейных сегментов необходимо установить факт наличия пересечения линий, принадлежащих двум разным объектам. Рассмотрим модель определения пересечения отрезков (рис. 6). Каждая прямая может быть выражена уравнением прямой с угловым коэффициентом в соответствии с (20). Прямые, которым принадлежат отрезки, будут задаваться уравнениями
где k1, b1 – угловой коэффициент и коэффициент смещения 1-й прямой (Р1, Р2); k2, b2 – угловой коэффициент и коэффициент смещения 2-й прямой (Р3, Р4). Если данные прямые имеют точку пересечения, то ее можно определить, для чего приравняем оба эти выражения и выразим х. Выражение для х будет иметь вид:
Подставив полученное выражение в формулу (24), можно определить вторую координату точки:
Таким образом, была определена точка пересечения прямых, на которых лежат линейные сегменты. После определения координат точки пересечения необходимо проверить ее принадлежность обоим линейным сегментам по формуле (12). Представляет интерес ситуация, когда линейные сегменты двух объектов находятся в соседстве, а сами объекты пересекаются. В этом случае необходимо проверять тройки смежных вершин: если «боковые» вершины будут лежать по разные стороны от линии, содержащей в себе линейный сегмент другого объекта, то данные объекты пересекаются. Установление пересечения линейных незамкнутых объектов выражается следующей последовательностью шагов: 1) формируются упорядоченные векторы вершин объектов А и В; 2) осуществляется поиск пересечений линейных сегментов рассматриваемых объектов; 3) если такие пересечения найдены, то объекты пересекаются, в противном случае – не пересекаются. Для установления факта соседства линейных незамкнутых объектов можно использовать следующую последовательность действий: 1) формируются упорядоченные векторы вершин объектов А и В; 2) выполняется поиск линейных сегментов, принадлежащих различным объектам, соответствующих одному из следующих вариантов: 2.1) линейные сегменты лежат на одной прямой, одна из граничных точек одного из сегментов принадлежит другому сегменту, 2.2) линейные сегменты лежат на различных прямых, граничная точка одного из линейных сегментов принадлежит другому линейному сегменту; 3) устанавливается, что линейные объекты не имеют пересечений. Линейный объект А будет вложен в линейный объект В, если все его сегменты (за исключением первого и последнего) будут совпадать с линейными сегментами объекта В, а первый и последний сегменты объекта А, будут вложены в линейные сегменты объекта В. Для установления факта изолированности линейных объектов необходимо определить, что эти объекты не состоят в отношении соседства, пересечения и вложенности. Для определения расстояния (расстояние допустимо находить только между изолированными объектами) используется следующий алгоритм: 1) выполняется последовательный просмотр вершин объекта А и находится минимальное из расстояний от любой его вершины до объекта В, 2) аналогичное действие выполняется относительно вершин объекта В, 3) за расстояние между объектами А и В принимается минимальное из найденных расстояний. При рассмотрении линейных замкнутых объектов нужно учитывать следующее: - объекты А и В будут изолированы, если не найдется такой вершины, принадлежащей объекту А(В), что она находится внутри объекта В(А); - установление соседства выполняется аналогично линейным разомкнутым объектам; - нахождение расстояния выполняется аналогично линейным разомкнутым объектам; - линейный разомкнутый (замкнутый) объект А вложен в линейный замкнутый объект В, если все его вершины вложены в объект В и нет пересечений линейных сегментов; - объекты А и В пересекаются, если вершина, принадлежащая объекту А(В), находится внутри объекта В(А). Рассмотренные алгоритмы и методы не охватывают работу с криволинейными объектами. Это вызвано тем, что городские карты содержат в основном объекты, состоящие из линейных сегментов (дома, улицы, кварталы и т.д.). Криволинейные сегменты используются для описания лишь топоосновы. Для проверки предлагаемых алгоритмов была разработана демонстрационная программа. В качестве инструментальной ГИС успешно использовалась ГИС «Ингео». Список литературы 1. Журкин И.Г., Наумов С.В. Итерационная модель представления линейных пространственных данных // Информационные технологии. - 2003, - № 6. - С. 11-16. 2. Андрианов Д.Е., Булаев А.В. Алгоритм представления сложных топологических отношений в геоинформационных системах // Тр. Рос. науч.-технич. об-ва радиотехники, электроники и связи им. А.С. Попова. Сер. Цифр. обработка сигналов и ее применение. - М., 2006. – Вып. VIII-2. - С. 604-606. 3. Власов М.Ю., Горбачев В.Г. Концептуальные топологические отношения // Инф. бюллетень ГИС-ассоциации. - 1996. - № 2(4). - С. 17. 4. Горбачев В.Г. Что такое «топологические» отношения в цифровой картографии и для чего топологические отношения нужны в геоинформатике? - www.integro.ru. 5. Садыков С.С., Андрианов Д.Е., Еремеев С.В. Формальное определение топологических отношений между картографическими объектами в ГИС // Обработка информации: методы и системы.: Сб. науч. ст. – М.: Горячая линия – Телеком, 2003. 6. Симаков Р.А., Булаев А.В. Модель данных муниципальной ГИС // Методы и системы обработки информации.: Сб. науч. ст.: в 2 ч. / Под ред. С.С. Садыкова, Д.Е. Андрианова – М., Горячая линия – Телеком, 2004. - Ч. 1. 7. Ласло Майкл. Вычислительная геометрия и компьютерная графика на С++/ Пеp. с англ. В. Львова. - М.: Бином, 1997. - 304 с.: ил. | ||||||||||||||
http://swsys.ru/index.php?id=457&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Параллельная обработка в алгоритмах визуализации с трассировкой лучей
- Потоковый анализ программ, управляемый знаниями
- Правила построения автоматизированных информационных систем экспертной оценки и согласования
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов

 В таких системах хранение пространственной информации связано с использованием модели данных. В настоящее время все больше применяется топологическая модель пространственных данных, позволяющая полностью реализовать возможности ГИС анализа [1].
В таких системах хранение пространственной информации связано с использованием модели данных. В настоящее время все больше применяется топологическая модель пространственных данных, позволяющая полностью реализовать возможности ГИС анализа [1]. Здесь можно отметить, что информация о реальном объекте представляет собой некоторую совокупность геометрических примитивов и нашу способность правильно трактовать эту совокупность. Каждый из примитивов находится в некотором отношении с другими, поэтому задачей любой ГИС является поддержка принятия более корректного решения. Для этого необходимо разработать модели и алгоритмы, основанные на топологических отношениях объектов и их частей.
Здесь можно отметить, что информация о реальном объекте представляет собой некоторую совокупность геометрических примитивов и нашу способность правильно трактовать эту совокупность. Каждый из примитивов находится в некотором отношении с другими, поэтому задачей любой ГИС является поддержка принятия более корректного решения. Для этого необходимо разработать модели и алгоритмы, основанные на топологических отношениях объектов и их частей. , (1)
, (1) , (6)
, (6)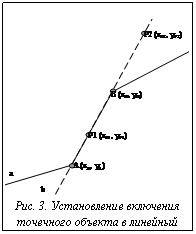
 (7)
(7) . (8)
. (8) . (9)
. (9) (10)
(10) , (11)
, (11) (12)
(12) если точечный объект проецируется на несколько линейных сегментов, то находим длины всех высот, опущенных из точечного объекта к линейным сегментам, на которые он проецируется, и выбираем наименьшую из них.
если точечный объект проецируется на несколько линейных сегментов, то находим длины всех высот, опущенных из точечного объекта к линейным сегментам, на которые он проецируется, и выбираем наименьшую из них. (13)
(13) (14)
(14) (15)
(15) . (16)
. (16) , где N – число вершин линейного объекта;
, где N – число вершин линейного объекта; , где K – число сегментов линейного объекта;
, где K – число сегментов линейного объекта; ;
; , (17)
, (17) . (18)
. (18) Зная угловой коэффициент прямой и коэффициент смещения, а также уравнение прямой, на которой лежит луч трассировки, можем найти координаты точки пересечения луча и линейного сегмента:
Зная угловой коэффициент прямой и коэффициент смещения, а также уравнение прямой, на которой лежит луч трассировки, можем найти координаты точки пересечения луча и линейного сегмента: (19)
(19) , (20)
, (20)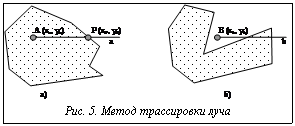 дан вектор L={l1,l2,…,lk-1}={(p1,p2),(p2,p3),…, (pk-1,pk)}, хранящий линейные сегменты, составляющие контур полигонального объекта;
дан вектор L={l1,l2,…,lk-1}={(p1,p2),(p2,p3),…, (pk-1,pk)}, хранящий линейные сегменты, составляющие контур полигонального объекта; (21)
(21) (22)
(22) . (23)
. (23) . (24)
. (24)