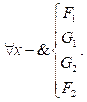Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Метод трансляции первопорядковых логических формул в позитивно-образованные формулы
Аннотация:В статье рассматриваются логическое исчисление позитивно-образованных формул (ПОФ-исчисление) и построенный на его основе метод автоматического доказательства теорем. ПОФ-исчисление впервые появилось в работах академиков РАН С.Н. Васильева и А.К. Жерлова в результате рассмотрения и решения задач теории управления и было описано как логический формализм первого порядка. Имеются примеры описания и решения задач теории управления, эффективно (с точки зрения выразительности языка и производительности средств доказательств теорем) решенных с помощью ПОФ-исчисления, например, управление группой лифтов, наведение телескопа на центр планеты, находящейся в неполной фазе, управление мобильным роботом. ПОФ-исчисление выгодно отличается от возможностей других, логических, средств формализации предметной области и поиска логических выводов выразительностью в сочетании с компактностью представления знаний, естественным параллелизмом их обработки, крупноблочностью и меньшей комбинаторной сложностью выводов, высокой совместимостью с эвристиками и широкими возможностями для интерактивного доказательства. В выделенном классе формул возможно построение конструктивного доказательства. Данный класс формул существенно шире класса хорновских дизъюнктов, используемых в языке Пролог: на логическую формализацию аксиоматической базы предметной области не накладываются никакие ограничения, а целевое утверждение – это конъюнкция запросов (в смысле языка Пролог). Для тестирования программной системы автоматического доказательства теорем (прувера), основанной на ПОФ-исчислении, использовалась библиотека задач TPTP (Thousands of Problems for Theorem Provers). Формат, в котором представлены задачи TPTP (называемые проблемами), де-факто стал стандартом среди сообщества, изучающего автоматизацию рассуждений. Возникает естественная необходимость в том, чтобы разрабатываемый прувер принимал на вход задачи в этом формате. Таким образом, возникла задача трансляции формул логики предикатов первого порядка, представленных в формате TPTP, в формат ПОФ. Эта задача нетривиальна из-за особой структуры формул ПОФ-исчисления. В данной работе предложены более эффективный (в сравнении с ранее разработанным алгоритмом в первой реализации системы автоматического доказательства теорем для ПОФ-исчисления) метод трансляции формул первопорядкового языка исчисления предикатов с сохранением исходной эвристической структуры знаний и его упрощенная версия для задач, представ-ленных на языке дизъюнктов. Под эффективностью понимаются количество шагов и длина получаемых формул. Предложенный метод был реализован в виде программной системы – транслятора языка первопорядковых логических формул в формате ТРТР в язык ПОФ. Приведены результа-ты тестирования разработанного метода, которые позволяют сделать вывод о том, что существует определенный класс первопорядковых формул, не принимаемый во внимание как особый существующими системами автоматического доказательства теорем, в то время как в ПОФ-исчислении для данного класса формул существуют специальные стратегии, повышающие эффективность поиска вывода.
Abstract:The paper considers the logic calculus of positively constructed formulas (PCF calculus) and based on it automated theorem proving (ATP) method. The PCF calculus was developed and described as a first-order logic formalism in works of S.N. Vassilyev and A.K. Zherlov as a result of formalizing and solv-ing problems of control theory. There are examples of describing and solving some control theory problems, effectively (from the point of view of the language expressiveness and the theorem proving means efficiency) solved using PCF calculus, for example, controlling a group of lifts; directing a tele-scope at the planet center, which is in an incomplete phase, and mobile robot control. Comparing to the capabilities of other logical means for subject domain formalization and logic conclusion search, the PCF calculus have the advantage of the expressiveness combined with the com-pactness of knowledge representation, the natural parallelism of their processing, large block size and lower combinatorial complexity of conclusions, high compatibility with heuristics, and great capabili-ties for interactive proof. The selected class of formulas makes it possible to build constructive proofs. This class of formulas is much wider than the class of Horn clauses used in the Prolog. There are no re-strictions in the logical formalization of the axiomatic base of the subject domain, and the target state-ment is a conjunction of queries (in terms of the Prolog). To test the ATP software system (prover) based on the PCF calculus the authors used the TPTP (Thousands of Problems for Theorem Provers) library. The TPTP format has become a standard in the community that studies automated reasoning. There is a natural need for the developed prover to ac-cept problems in this format as input. Thus, the problem of translating the first-order predicate logic formulas presented in the TPTP format to the POF format arises. This problem is nontrivial due to the special structure of the PCF calculus formulas. The paper proposes a more efficient translation method (compared to the previously developed al-gorithm in the first implementation of the prover based on the PCF calculus) for the first-order predi-cate calculus language preserving the original heuristic knowledge structure, and its simplified version for the problems presented in language of clauses. The efficiency is a number of steps and the length of the obtained formulas. The proposed method was implemented as a software system – a language trans-lator of first-order TPTP logic formulas to the PCF calculus language. The paper presents test results of the developed method, which imply that there is a certain class of first-order formulas that are not tak-en into account as special by existing ATP systems, while the PCF calculus has special strategies that increase the efficiency of the inference search for such class of formulas.
| Авторы: Давыдов А.В. (andrey.davydov@datadvance.net) - Компания «ДАТАДВАНС» (технический писатель), Москва, Россия, Ларионов А.А. (bootfrost@zoho.com) - Институт динамики систем и теории управления им. В.М. Матросова СО РАН (программист), Иркутск, Россия, Черкашин Е.А. (eugeneai@icc.ru ) - Институт динамики систем и теории управления им. В.М. Матросова СО РАН (старший научный сотрудник), Иркутск, Россия | |
| Ключевые слова: алгоритмы трансляции, автоматическое доказательство теорем, математическая логика |
|
| Keywords: translation algorithms, automated theorem proving, mathematical logic |
|
| Количество просмотров: 6128 |
Статья в формате PDF Выпуск в формате PDF (4.91Мб) |
Сегодня активно развиваются автоматическое доказательство теорем (АДТ) и его приложения, о чем свидетельствуют, например, работы ежегодной конференции CADE, на секции System description которой или представляются новые системы для АДТ, или показывается развитие ранее разработанных. В данной статье рассматриваются логиче- ское исчисление позитивно-образованных формул (ПОФ-исчисление) и построенный на его основе метод АДТ. ПОФ-исчисление выгодно отличается от возможностей других, ло- гических, средств формализации предметной области и поиска логических выводов вырази- тельностью в сочетании с компактностью представления знаний, естественным параллелизмом их обработки, крупноблочностью и меньшей комбинаторной сложностью выводов, высокой совместимостью с эвристиками и более широкими возможностями для интерактивного доказательства. В выделенном классе формул возможно построение конструктивного доказательства. Данный класс существенно шире класса хорновских дизъюнктов, используемых в Прологе: на логическую формализацию аксиоматической базы предметной области не накладывается никаких ограничений, а целевое утверждение – это конъюнкция запросов в смысле языка Пролог. Понятие ПОФ-исчисления появилось в работах в результате описания и решения задач теории управления [1, 2]. ПОФ-исчисление описано в них как логический формализм первого порядка; приводятся примеры описания и решения задач теории управления, эффективно (с точки зрения выразительности языка и производительности средств доказательств теорем) решенных с помощью ПОФ-исчисления, например, управление группой лифтов, наведение телескопа на центр планеты, находящейся в неполной фазе, управление мобильным роботом, а также доказательства корректности и полноты исчисления. Для тестирования программной системы АДТ [3], основанной на ПОФ-исчислении, использовалась библиотека задач TPTP (Thousands of Problems for Theorem Provers) [4]. Формат, в котором представлены задачи TPTP (называемые проблемами), де-факто стал стандартом среди сообщества, изучающего автоматизацию рассуждений. На сайте библиотеки TPTP представлены многие системы АДТ, например, имеющая более чем двадцатилетнюю историю система Vampire [5] или одна из новых систем Scavenger [6] и др. А в работе [7] рассматривается программа-конвертер из формата SMT-LIB в формат TPTP. Появляется естественная необходимость в том, чтобы разрабатываемый прувер принимал на вход задачи в этом формате. Таким образом, возникла не- обходимость трансляции формул логики предикатов первого порядка, представленных в формате TPTP, в формат ПОФ. Эта задача нетривиальна из-за особой структуры формул ПОФ-исчисления. В данной работе предложен более эффективный (в сравнении с ранее разработанным алгоритмом в первой реализации системы автоматического доказательства теорем для ПОФ-исчисления [8]) метод трансляции. Под эффективностью понимаются количество шагов и длина получаемых формул. Приведены результаты тестирования разработанного метода, которые позволяют сделать вывод о том, что существует определенный класс первопорядковых формул, не принимаемый во внимание как особый системами АДТ, в то время как в ПОФ-исчислении для данного класса формул есть специальные стратегии, повышающие эффективность поиска вывода. Использование специальных стратегий вывода является перспективным направлением в области АДТ, в частности, в работе [9] приводится язык стратегий для прувера Isabelle/HOL. Предварительные определения. Будем говорить о языке первопорядковых логических формул (ПЛФ), построенных на основе атомарных формул с помощью связок &, Ú, Ø, ®, «, кванторов ", $ и констант True, False. Понятия «терм», «атом», «литера» определяются обычным образом. Пусть X = {x1, …, xk} – множество переменных, A = {A1, …, Am} – множество атомарных формул, F = {F1, …, Fn} – множество подформул. Тогда формулы (("x1)…("xk)(A1 &…& Am ® (F1 Ú…ÚFn))), (($x1) …($xk)(A1 &…& Am & (F1 &…&Fn))) будем обозначать как "XA:F и $XA:F соответственно, имея в виду, что "-квантор соответствует ®FÚ, где FÚ означает дизъюнкцию всех подформул из F, а $-квантор соответствует ®F&, где F& означает конъюнкцию всех подформул из F. Если F = Æ, формулы имеют вид "XA:Æ º º "XA ® False и $XA:Æ º $XA & True, так как дизъюнкция пустого количества элементов соответствует False, в то время как конъюнкция пустого количества элементов соответствует True. Будем записывать такие формулы, соответственно, "XA и $XA. Если X = Æ, тогда "A:F и $A:F также являются сокращением. Множество атомов A называется конъюнктом. Еще раз отметим, что пустой конъюнкт эквивалентен True. Переменные из X связаны соответствующими кванторами и называются соответственно "-переменными и $-переменными. В "XA переменные из X, которые не встречаются в конъюнкте A, называются неограниченными переменными. Конструкции "XA и $XA называются позитивными типовыми кванторами. Поскольку A является конъюнкцией только лишь положи- тельных атомов, эту конъюнкцию также называют типовым условием для X. На практике такие конструкции обозначают, например, фразы: «для любого X, удовлетворяющего A, следует…», «существует X, удовлетворяющее условию A, такое что…» или «Для всех целых чисел x, y, z и n > 2 выполнимо xn + yn ≠ zn». Изначально термин «типовый квантор» был предложен Николя Бурбаки как часть обозначений для формализации математики, однако типовые кванторы оказались применимыми и в других областях. Язык ПОФ Определение ПОФ. Пусть X – множество переменных, A – конъюнкт. · $XA и "XA называются $-ПОФ и "-ПОФ соответственно. · Если F = {F1, …, Fn} является "-ПОФ, тогда $XA:F будет называться $-ПОФ. · Если F = {F1, …, Fn} является $-ПОФ, тогда "XA:F будет называться "-ПОФ. · Всякая $-ПОФ и "-ПОФ будет называться ПОФ. Такое представление логических формул называется ПОФ, так как они записываются только с помощью позитивных типовых кванторов. Формулы не содержат знак отрицания в явном виде. Любая ПЛФ может быть представлена в виде ПОФ [2]. Таким образом, ПОФ есть особая форма записи классических формул языка предикатов подобно КНФ, ДНФ и др. Те ПОФ, которые начинаются с "Æ, называются ПОФ в канонической форме. Любая ПОФ может быть приведена к канонической. Пусть F – это $-ПОФ, тогда формула "Æ: F º º True ® F º F. Если F – это неканоническая "-ПОФ, тогда "Æ: {$Æ: F} º True ® {True & & F} º F. Типовые кванторы "Æ и $Æ называются фиктивными, так как они не влияют на истинностное значение исходной ПОФ, а только служат конструкциями, сохраняющими корректную запись ПОФ. Для удобства читаемости формул будем представлять их в древовидной форме. Запись QXA:{F1, …, Fn} эквивалентна
где Q – некоторый квантор. Элементы дерева называются как обычно: узел, корень, лист, ветвление и т.д. Поскольку "-кванторы соот- ветствуют дизъюнкциям подформул {F1, …, Fn}, а кванторы $ соответствуют конъюнкции, все "-узлы соответствуют дизъюнктивному ветвлению, а $-узлы конъюнктивному. Некоторые части канонической ПОФ будем называть следующим образом: – корень ПОФ "Æ называется корнем ПОФ; – каждый непосредственный последователь $XA корня ПОФ называется базой; конъюнкт A называется базой фактов; ПОФ, корнем которой является база, называется базовой подформулой; – каждый непосредственный последователь "YB базы ПОФ называется вопросом к своей базе; если вопрос является листом дерева, то он называется целевым вопросом; – поддеревья вопросов называются консеквентами; пустая консеквента эквивалента False. Пример. Рассмотрим ПОФ-представление некоторой ПЛФ: F = Ø("x$y P(x, y) ® $z P(z, z)). Образом F в языке ПОФ является F’=":Æ{"x:Æ{$y:P(x, y)}, "z:P(z, z){$:False}}. Последняя ПОФ в древовидной форме имеет следующий вид:
Описание шагов метода трансляции. Метод трансляции состоит из следующих шагов. Шаг 1. Преобразование задачи TPTP в ПЛФ. Полученная ПЛФ представляет собой отрицание конъюнкции всех формул, входящих в аннотированные формулы. Отрицание производится с той целью, что система АДТ опровергает отрицание исходной формулы, тем самым подтверждая ее доказуемость. Шаг 2. Удаление связок ®, «, снятие двойного отрицания и применение законов де Моргана. Пусть F (возможно, с индексом) – произвольная неатомарная ПЛФ, A – атомарная ПЛФ. Тогда имеем правила преобразований (назовем эту группу преобразований Tr1), представленные в таблице 1. Шаг 3. Уплощение конъюнкций и дизъюнкций. Пусть ·Î{Ú, &}. Правило уплощения дизъюнкций и конъюнкций flat. Пусть F = G1·…·Gn·C1·…·Cm, где Ci = = (Ci1·…·Ciki), тогда Fflat = G1 ·…·Gn & C11 ·… ·C1k1 ·… ·Cm1 ·… ·Cmkm. Таблица 1 Правила преобразования Tr1 Table 1 Tr1 transformation rules
Смысл «уплощения» хорошо виден, если формулу представить синтаксическим деревом. Например, следующие требования эквивалентны:
Шаг 4. Трансляция ПЛФ в ПОФ. Пусть G (возможно, с индексами) есть некоторая ПЛФ, а A (возможно, с индексами) – атомарная ПЛФ. Введем еще одно обозначение. Пусть P, Q Î {", $}, P ≠ Q, а C – некоторый конъюнкт, тогда: Правила преобразования Tr2 можно представить в виде таблицы 2. Правило уплощения позволяет ограничить, насколько это возможно, применение правил 13 и 14, которые приводят к появлению фиктивных кванторов. Шаг 5. Правило сокращения. В получаемой формуле возникают узлы с фиктивными кванторами "Æ и $Æ, кроме этого, могут возникнуть излишние ветвления, плохо влияющие на дальнейший поиск логического вывода. Следующее правило позволяет максимально сократить получаемое дерево. Если в некоторой ПОФ F
P, Q Î {", $}, P ≠ Q, C, B – конъюнкты, удовлетворяющие условию C Í B, то F эквивалентна F¢, имеющей следующий вид:
Представленное правило нуждается в доказательстве. Пусть конъюнкт C имеет вид C1 & … & Cm. Если C Í B, то B = B¢ & C1 & … & Cm, где B¢ – некоторый, возможно, пустой конъюнкт. Переведем ПОФ F в язык исчисления предикатов. В случае, если F начинается с квантора ": F = "xA ®(FÚ$Y(Y&B(ØCÚ$z1(D1&F1)Ú… Ú (Dk&Fk)))). При раскрытии скобок получаем дизъюнкцию конъюнкций, одна из которых
Поэтому F="xA®(FÚ$Y$Y1(B&D1&Y&F1)Ú … Ú (B&Dk&Y&Fk)), что при переводе в ПОФ-представление имеет вид, совпадающий с F¢. Если F начинается с квантора $, то после перевода в язык исчисления предикатов получаем: F = $XA&Ф&
Распишем выражение в скобке:
Устраняем импликацию и группируем дизъюнктивные элементы в отдельную скобку:
Применяя закон дистрибутивности, получаем:
В первых n скобках присутствует тавтология ¬CiÚ¬Ci, поэтому
То есть
что при переводе в ПОФ-представление имеет вид, совпадающий с F¢. Доказательство завершено. В библиотеке TPTP, кроме задач в классическом первопорядковом представлении, достаточно большое количество задач представлено в виде множеств дизъюнктов, задачи приведены в скулемовской стандартной форме и восстановить их первоначальную формализацию проблематично. Для перевода задач, представленных в виде множеств дизъюнктов, в которых отсутствуют переменные, связанные кванторами существования, достаточно воспользоваться приведенной ниже формулой. Объединим дизъюнкты некоторого множества S в классы C1, C2, C3, C4, которые представляются следующим образом: · · · · ПОФ, соответствующая упорядоченному таким образом множеству дизъюнктов, будет иметь вид:
Тестирование. Для систем АДТ важно время, затраченное на решение задачи. Поскольку разработанный транслятор (включая синтаксический анализатор) планируется использовать в системе АДТ для ПОФ-исчисления, эффективность трансляции также важна. Эффективность работы программы в целом может зависеть от двух факторов: качества генерируемого кода компилятором (либо скорости исполнения интерпретатором) и качества используемых алгоритмов. Важными характеристиками полученной в результате трансляции ПОФ являются количество узлов в древовидном представлении ПОФ и количество фиктивных кванторов. Поэтому процедура трансляции ПЛФ в ПОФ состоит из нескольких шагов, часть из которых направлены на уменьшение количества узлов и фиктивных кванторов. Исходная эвристическая структура ПЛФ сохраняется благодаря тому, что сохраняются кванторы " и $ и их исходный порядок следования (в отличие от процедуры скулемизации, используемой для получения КНФ, устраняющей кванторы $ и вносящей в формулы дополнительные термы). Алгоритм трансляции написан на языке Rust [10]. Тестирование разработанных алгоритмов производилось на задачах из библиотеки TPTP. Использовался компьютер MacBookPro с процессором 2,3 GHz Intel Core i7 и оперативной памятью 8 GB 1 600 MHz DDR3. Всего было отобрано 6 817 задач, по которым собиралась статистика. Количество задач, для которых ПЛФ-представление содержит меньше узлов, чем ПОФ-представление, равно 1 169. В таблице 3 представлены 10 таких задач. Количество задач, для которых ПОФ-представление содержит меньше узлов, чем ПЛФ-представление, равно 5 648, 10 из них приведены в таблице 4. В таблице 5 показаны 5 наиболее трудоемких для трансляции задач. Кроме того, не обнаружено никакой зависимости между рейтингом задачи и наличием в ней неограниченных переменных в ПОФ-представлении данной задачи. Этот факт говорит о том, что для систем АДТ, основанных на методе резолюций, не имеет значения, содержит ли формализация задачи неограниченные переменные. Однако для метода АДТ, основанного на ПОФ-исчислении, отсутствие неограниченных переменных заметно улучшает эффективность поиска логического вывода. Поэтому с помощью ПОФ-исчисления естественным об- Заключение В работе приводится краткое описание языка ПОФ и рассматриваются вопросы их обработки перед запуском автоматических алгоритмов поиска вывода. Представлен метод пре- образования ПЛФ в язык ПОФ в виде эффективных алгоритмов обработки первопорядковых формул. Разработанные алгоритмы сохраняют исходную эвристическую структуру знаний, представленных формулами языка исчисления предикатов. Рассмотрены вопросы преобразования формул языка дизъюнктов в язык ПОФ, и предложен упрощенный алгоритм для трансляции таких задач. Работа выполнялась при поддержке РФФИ, проект № 16-29-04238офи_м. Литература 1. Vassiliev S.N. Machine synthesis of mathematical theorems. J. Logic Program., 1990, vol. 9, no. 2–3, pp. 235–266. 2. Васильев С.Н., Жерлов А.К., Федунов Е.А., Федосов Б.Е. Интеллектное управление динамическими системами. М.: Физматлит, 2000. 352 с. 3. Cherkashin E.A., Davydov A.V., Larionov A.A. Calculus of positively-constructed formulas, its features strategies and implementation. Proc. 36-th Intern. Convent. MIPRO 2013/CIS, Chroatia, Opatija, 2013, pp. 1289–1295. 4. Sutcliffe G. The TPTP problem library and associated infrastructure. The FOF and CNF parts, v3.5.0. J. Autom. Reason., 2009, vol. 43, no. 4, pp. 337–362. DOI: 10.1007/s10817-009-9143-8. 5. Kovács L., Voronkov A. First-order theorem proving and Vampire. Proc. 25th Conf. CAV, LNCS, 2013, vol. 8044, pp. 1–35. DOI: 10.1007/978-3-642-39799-8_1. 6. Itegulov D., Slaney J., Woltzenlogel Paleo B. Scavenger 0.1: A theorem prover based on conflict resolution. In: de Moura L. (eds.). Proc. 26th Conf. CADE, LNCS, 2017, vol. 10395, pp. 344–356. DOI: 10.1007/978-3-319-63046-5_21. 7. Baumgartner P. SMTtoTPTP – a converter for theorem proving formats. Proc. 25th Intern. Conf. CADE, LNCS, 2015, vol. 9195, pp. 285–294. 8. Черкашин Е.А. Программная система «КВАНТ/1» для автоматического доказательства теорем. Иркутск: Изд-во ИДСТУ СО РАН, 1999. 16 с. 9. Nagashima Y., Kumar R. A proof strategy language and proof script generation for Isabelle/HOL. Proc. 26th Conf. CADE, LNCS, 2017, vol. 10395, pp. 528–545. DOI: 10.1007/978-3-319-63046-5_32. 10. Rust Programming Language. URL: www.rust.org (дата обращения: 25.03.2019). References
|
| Постоянный адрес статьи: http://swsys.ru/index.php?id=4642&like=1&page=article |
Версия для печати Выпуск в формате PDF (4.91Мб) |
| Статья опубликована в выпуске журнала № 4 за 2019 год. [ на стр. 556-564 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик: