Гибридный нейросетевой алгоритм идентификации сложных объектов
| Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук, Санатин Д.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
|
|
|
Как известно, выделяют два основных вида аппроксимационных моделей: параметрические и непараметрические (локально-параметрические) [1,2]. При параметрическом подходе вначале выбирается аппроксимирующая зависимость, затем на основе обучающей выборки адаптируются ее параметры. К параметрическим методам моделирования относятся полиномиальные нейронные сети (Σ-Π нейронные сети), многослойные персептроны [3,4] и др. Если правильно подобрана аппроксимирующая зависимость, то качество моделирования весьма высоко даже в случае небольшой или зашумленной обучающей выборки [1,2] и наоборот. При непараметрическом подходе вначале выбирается тип аппроксимирующей зависимости, но в данном случае по экспериментальным данным строится большое количество указанных зависимостей, каждая из которых имеет свои параметры. К непараметрическим методам моделирования относятся метод М-ближайших узлов [1,2], нейронные сети с радиальными базисными элементами [3,4]. Достоинством непараметрических методов является отсутствие необходимости выбирать тип глобальной аппроксимирующей зависимости. Отклик модели в непараметрических методах определяется не всей, а лишь частью обучающей выборки, что делает такие модели малоэффективными при значительной зашумленности обучающей выборки.
Предположим, что исследуемый статический объект имеет
где Функция
где
(в которой Для функций
где
Предположим далее, что на объекте реализован эксперимент, заключающийся в регистрации
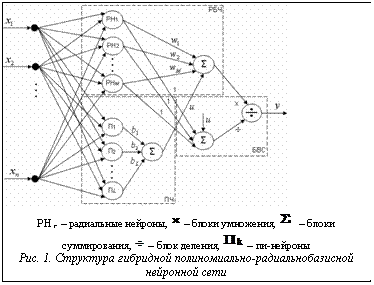
при этом значения Требуется на основе экспериментальных данных (5) восстановить неизвестную зависимость Гибридная полиномиально-радиальнобазисная искусственная нейронная сеть В работе [5] сформулирован принцип адекватности, согласно которому объект и его система моделирования или управления для наиболее оптимального решения задачи должны обладать рядом общих черт. В соответствии с принципом адекватности для решения рассматриваемой задачи предложена гибридная полиномиально-радиальнобазисная искусственная нейронная сеть (HPRBFN, от Hybrid polynomial radial basis function network), структурно состоящая из радиально-базисной части (РБЧ), полиномиальной части (ПЧ) и блока взвешенного суммирования (БВС) (рис. 1). Предложенная искусственная нейронная сеть реализует следующую нелинейную зависимость:
где
Подходы к формированию HPRBFN и базовый алгоритм ее обучения Формирование HPRBFN на основе обучающей выборки (5) состоит в последовательной реализации трех этапов. 1. Формирование ПЧ сети в предположении, что РБЧ отсутствует (
где Из формулы (9) видно, что формирование ПЧ заключается в определении количества пи-нейронов L и значений параметров данных нейронов Структура полиномиальной зависимости может выбираться как на основе информации о предметной области, так и путем оптимизации вида данной зависимости, например с использованием метода группового учета аргументов [4]. 2. Формирование РБЧ сети в предположении, что ПЧ отсутствует (
Из формулы (10) видно, что формирование РБЧ заключается в определении числа радиальных нейронов M, значений параметров При формировании РБЧ сети могут использоваться методы, разработанные для создания и обучения RBFN сетей [3,4]. 3. Настройка параметра Рассмотрим базовый алгоритм обучения HPRBFN. Шаг 0 (предварительный). Обучающая выборка (5) разбивается на две части: собственно обучающую
и контрольную
выборки (H+L=N). Размер контрольной выборки Шаг 1. Определение вектора параметров Вариант А. С использованием нерекуррентного метода наименьших квадратов (МНК) [3,4]:
где Вариант B. С использованием рекуррентного МНК [3, 4]:
где
Шаг 2. Определение числа радиальных нейронов M, значений параметров 1) Устанавливаются переменные i=1 и M=0. 2) Из обучающей выборки извлекается элемент
где 3) Если 4) Если i= N, то останов, иначе i=i+1 и переход к пункту 2. Шаг 3. Определение значения параметра отклонения радиальных нейронов Вариант А. С использованием эмпирической формулы:
где Вариант B. С использованием алгоритма оптимизации. Нейронная сеть обучается по обучающей выборке (11), после чего параметр
где 4. Настройка параметра u с использованием алгоритма оптимизации. Нейронная сеть обучается по обучающей выборке (11), после чего параметр u определяется путем минимизации ошибки на тестирующей выборке (12):
где Метод золотого сечения [6]. Предположим, необходимо найти минимум функции Шаг 1. Устанавливаются переменные: k=1,
Шаг 2. Если
иначе
Шаг 3. Проверяется критерий останова Вычислительный эксперимент Предположим, что объект имитируется зависимостью вида (1), при этом
где Аддитивная помеха На рисунке 2 показан график СКО моделей в зависимости от параметра Для обучения HPRBFN используется базовый алгоритм, описанный выше. Из приведенных на рисунке 2 зависимостей видно, что предложенная HPRBFN при малых значениях параметра q обеспечивает точность модели, близкую к полиномиальной МНК модели, при больших значениях q – близкую к точности GRNN, и в среднем дает наилучший из всех методов результат. Сложные объекты, имеющие существенную полиномиальную составляющую (см. (2)) достаточно широко распространены на практике в экономике, медицине, технике и т.п., вследствие чего предложенные полиномиально-радиальнобазисные нейронные сети могут найти широкое применение в системах моделирования и управления. Список литературы 1. Катковник В.Я. Непараметрическая идентификация и сглаживание данных. - М.: Наука, 1985. 2. Дли М.И. Локально-аппроксимационные модели сложных объектов. - М.: Наука; Физматлит, 1999. 3. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Горячая линия – Телеком, 2001. 4. Дюк В., Самойленко А. Data Mining: Учебный курс. - СПб.: Питер, 2001. 5. Ивахненко А.Г. Самообучающиеся системы распознавания и автоматического управления. - К.: Технiка, 1969. 6. Банди Б. Методы оптимизации: Вводный курс. - М.: Радио и связь, 1988. |
http://swsys.ru/index.php?id=465&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Эволюционная модель формирования структур виртуальных предприятий
- Формирование программ развития больших систем административно-организационного управления
- Формулировка задачи планирования линейных и циклических участков кода
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Инженерная программа трехмерного моделирования магнитных систем LittleMag

 В настоящей статье предложена гибридная полиномиально-радиальнобазисная нейронная сеть, позволяющая совместить достоинства как параметрического, так и непараметрического подходов.
В настоящей статье предложена гибридная полиномиально-радиальнобазисная нейронная сеть, позволяющая совместить достоинства как параметрического, так и непараметрического подходов. входов (векторный вход
входов (векторный вход  ) и один выход
) и один выход  . Связь между
. Связь между  и
и  в n-мерной области
в n-мерной области  может быть адекватно представлена моделью:
может быть адекватно представлена моделью: , (1)
, (1) – функция неизвестного вида;
– функция неизвестного вида;  – аддитивная случайная помеха (отражает действие неучитываемых факторов) с нулевым математическим ожиданием и неизвестным распределением на
– аддитивная случайная помеха (отражает действие неучитываемых факторов) с нулевым математическим ожиданием и неизвестным распределением на  .
. , (2)
, (2) – полиномиальная функция:
– полиномиальная функция: , (3)
, (3) – постоянные параметры;
– постоянные параметры;  – целый положительный параметр;
– целый положительный параметр;  – целые неотрицательные параметры);
– целые неотрицательные параметры);  – нелинейная функция общего вида.
– нелинейная функция общего вида. , (4)
, (4) – функционал, возвращающий среднеквадратичное значение функции-аргумента в области
– функционал, возвращающий среднеквадратичное значение функции-аргумента в области  ,
, 
 .
. пар значений:
пар значений: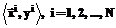 , (5)
, (5) .
. , (6)
, (6) ,
,  – весовые коэффициенты;
– весовые коэффициенты;  ,
,  – функции, реализуемые радиальными нейронами и ПЧ сети соответственно:
– функции, реализуемые радиальными нейронами и ПЧ сети соответственно: , (7)
, (7) , (8)
, (8) – евклидова векторная норма;
– евклидова векторная норма;  ,
,  ,
,  – постоянные параметры;
– постоянные параметры;  – целый положительный параметр;
– целый положительный параметр;  – целые неотрицательные параметры.
– целые неотрицательные параметры. ). В рассматриваемом случае выражение (6) принимает вид:
). В рассматриваемом случае выражение (6) принимает вид: , (9)
, (9) ,
,  .
. , а также весовых коэффициентов
, а также весовых коэффициентов  ). В рассматриваемом случае выражение (6) принимает вид:
). В рассматриваемом случае выражение (6) принимает вид: . (10)
. (10) и
и  (11)
(11) (12)
(12) , где заданный параметр
, где заданный параметр  ; по умолчанию выбирается
; по умолчанию выбирается  . Устанавливается параметр R – минимально допустимое расстояние между центрами радиальных нейронов.
. Устанавливается параметр R – минимально допустимое расстояние между центрами радиальных нейронов. ПЧ сети.
ПЧ сети.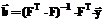 , (13)
, (13) ,
,  .
. , (14)
, (14) ,
, ,
, .
. и находится минимальное расстояние:
и находится минимальное расстояние: , (15)
, (15) .
. , то добавляется радиальный нейрон с параметрами
, то добавляется радиальный нейрон с параметрами  , устанавливаются
, устанавливаются  и M =M+1.
и M =M+1. , (16)
, (16) ,
,  – максимальное и минимальное значения компонент входного вектора
– максимальное и минимальное значения компонент входного вектора  , (17)
, (17) – отклик обученной сети при подаче на ее вход
– отклик обученной сети при подаче на ее вход  . Для решения задачи (17) используется метод золотого сечения [6].
. Для решения задачи (17) используется метод золотого сечения [6]. , (18)
, (18) – отклик обученной сети при подаче на ее вход
– отклик обученной сети при подаче на ее вход  на отрезке
на отрезке  с заданной точностью
с заданной точностью  . Алгоритм состоит в реализации следующих шагов.
. Алгоритм состоит в реализации следующих шагов. ,
,  ,
,  ,
,  . Вычисляются значения:
. Вычисляются значения:

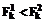 , то
, то  ,
,  ,
,  ,
,  ,
, ,
,  ,
, ,
,  ,
,  ,
,

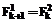 ,
, .
. . Если указанный критерий не выполнен, то
. Если указанный критерий не выполнен, то  и переход к шагу 2. В противном случае останов, решением считается
и переход к шагу 2. В противном случае останов, решением считается  .
.



 – постоянный параметр,
– постоянный параметр, 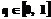 .
. и среднеквадратичной ошибкой (СКО)
и среднеквадратичной ошибкой (СКО)  . Аппроксимация производится в области
. Аппроксимация производится в области 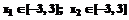 . Обучающая выборка расположена в области
. Обучающая выборка расположена в области  (LA5) [2]; многослойный персептрон со структурой 12-5-1 (MLP) [3]).
(LA5) [2]; многослойный персептрон со структурой 12-5-1 (MLP) [3]).