Программные продукты и системы

Интеллектуальные технологии управления прочно входят во все сферы человеческой деятельности. Известны подходы к управлению техническими объектами, основанные на нечеткой логике, нейронных и нейро-нечетких сетях. Внедрение интеллектуальных технологий в системы управления определяется лучшими показателями качества переходных процессов, более широкими возможностями к парированию возмущений и робастностью при изменении параметров функционирования. Вместе с тем зачастую отмечается уменьшение перерегулирования и длительности переходного процесса при управлении техническими объектами.

Информация о поведении того или иного технического объекта доступна экспертам, которые могут быть привлечены к разработке интеллектуальных регуляторов. При рассмотрении области интеллектуального управления на основе нечеткой логики возникают трудности определения количества термов в терм-множе- ствах лингвистических переменных (ЛП), вида и параметров функций принадлежности. Получили распространение треугольные функции принадлежности для снижения вычислений при определении степени принадлежности значений сигналов. В соответствии с рекомендациями терм-множества ЛП могут содержать до семи термов, что определяется сложностью разработки базы нечетких правил. Допустим, у нечеткого регулятора имеются две входные ЛП с тремя термами каждая, тогда полная база нечетких правил должна содержать 9 правил (то есть 3 ´ 3), что, очевидно, не вызовет затруднений у эксперта при ее разработке. Но при тринадцати термах у каждой входной ЛП база нечетких правил должна содержать 169 правил, и эксперту будет затруднительно составить ее без ошибок.

Также необходимо исключить возникновение избыточных (дублирующих) правил в базе, что требует от эксперта особого внимания. При этом наличие правил с одинаковым антецедентом, но разным консеквентом приводит к возникновению неопределенности. Неполнота базы правил может вызвать ситуацию, когда в базе не найдется правила, соответствующего текущим входным сигналам нечеткого регулятора. Такие базы правил можно использовать только в случае полной уверенности в невозможности подобного.

Таким образом, снижение трудоемкости разработки нечетких регуляторов и автоматизация процесса определения их параметров являются перспективными и востребованными направлениями исследований. В данной статье предложен метод автоматического синтеза нечетких регуляторов на основе измерений, снятых с системы управления с ПИ-регулятором, показан подход к определению параметров функций принадлежности ЛП и составлению базы правил в автоматическом режиме. Отдельно рассмотрен механизм редуцирования базы правил. Достоинством метода является возможность его использования независимо от вида и количества входных сигналов. Это могут быть сигнал ошибки, ее интеграл, производные и т.п.

Обзор публикаций

На сегодняшний день существует большое количество публикаций, посвященных интеллектуальным технологиям управления техническими объектами. Рассмотрим некоторые из них, непосредственно связанные с автоматизацией синтеза нечетких регуляторов, и определим основные направления исследований.

Например, в работе [1] предложен метод синтеза нечеткого регулятора на основе исходных данных о результатах работы классических регуляторов, таких как ПИД, ПИ, ПД и др. В основе метода лежит идея создания обучающей выборки вида вход-выход классического регулятора и ее использования для тренировки нечеткой модели Такаги–Сугено. Данный метод предполагает участие человека в процессе формирования терм-множеств ЛП нечеткого регулятора.

В работе [2] предложен метод синтеза базы управляющих правил нечеткого регулятора на основе кластерного анализа и генетического алгоритма. Его отличительной особенностью является наличие возможности контроля процесса настройки параметров нечеткого регулятора с целью предотвращения переобучения.

В работе [3] представлен метод оптимиза- ции количества управляющих правил нечеткого регулятора. Его основная идея заключается в выявлении и последующем объединении противоречивых правил, то есть имеющих одинаковые части условия (антецеденты) и разные заключения (консеквенты). Метод не улучшает эффективность работы нечеткого регулятора, в чем и есть его основной недостаток.

В работе [4] предложен метод оптимизации параметров нечеткого регулятора, позволяющий уменьшить количество применяемых нечетких правил. Основная идея метода заключается в приведении терм-множеств ЛП нечеткого регулятора к более простому виду с последующей проверкой эффективности выполненных преобразований. Рассмотрена ситуация, в которой несколько нечетких правил объединяются в одно, если новый вид функций принадлежности более предпочтителен и допускает это.

В работе [5] описан метод решения задачи синтеза базы правил нечеткого контроллера с ее последующим анализом и оптимизацией с использованием генетического алгоритма. Отличие метода в применении двух способов кодирования параметров нечеткого регулятора и, соответственно, в структуре получаемых хромосом. Применяемый в методе способ коррекции противоречивых правил подобен изложенному в [3] и имеет аналогичные недостатки.

В работе [6] предложен метод автоматической генерации управляющих правил нечеткого регулятора для решения задач классификации на основе статистической выборки, содержащей численные признаки объектов определенных классов. Отличительная особенность метода заключается в возможности генерации минимального количества правил, необходимого для эффективного решения поставленной задачи управления. Это достигается за счет анализа важности отдельных правил с последующим назначением им соответствующих весовых коэффициентов и объединением с аналогичными по смыслу правилами, уже существующими в базе.

В работе [7] предложен метод генерации базы правил нечеткого регулятора с использованием генетического алгоритма. Используемый в процессе синтеза нечеткого регулятора статистический набор данных аналогичен применяемому в работе [6]. Отличительной особенностью метода является использование интегральной функции приспособленности для генетического алгоритма, позволяющей комплексно оценивать параметры нечеткого регулятора и точность его работы. По сравнению с результатами работы [6] количество нечетких правил уменьшено в несколько раз при одновременном увеличении точности работы.

В работе [8], как и в [7], для синтеза нечеткого контроллера используется генетический алгоритм. Предлагаемый метод отличается отсутствием необходимости предварительного определения параметров нечеткого регулятора пользователем и использованием модифицированного алгоритма кластеризации данных.

Работа [9] по содержанию близка к работам [7, 8]. Ее основное отличие заключается в виде используемой функции приспособленности генетического алгоритма и способе формирования хромосом на основе параметров нечеткого регулятора.

В работе [10] предложен генетический алгоритм, позволяющий автоматически создавать базу управляющих правил нечеткого регулятора. Основное отличие этого метода от аналогов [4, 8] заключается в использовании специальной метрики, характеризующей степень противоречивости управляющих правил. Применение указанной метрики в качестве одного из слагаемых функции оценки генерируемых решений делает конечный результат более оптимальным.

По результатам обзора публикаций можно выделить направления автоматического синтеза нечетких регуляторов, связанные с применением генетических алгоритмов и методов кластеризации. Генетические алгоритмы позволяют достичь высоких результатов для автоматического синтеза нечетких регуляторов, но их использование ограничивается априорно заданным количеством входных и выходных ЛП и типом используемых функций принадлежности, то есть при изменении исходных данных есть необходимость в перенастройке генетического алгоритма или даже его изменении. Методы кластеризации лишены указанного недостатка и позволяют синтезировать нечеткие регуляторы при изменении исходных данных. Современные методы кластеризации не только оперируют априорно заданным количеством кластеров при анализе массивов данных, но и позволяют определить их количество самостоятельно.

Кроме того, можно отметить высокое быстродействие методов синтеза нечетких регуляторов, основанных на кластеризации массивов данных.

Метод автоматического синтеза нечетких регуляторов

В данной работе используются результаты, полученные авторами при разработке теоретических основ и методов автоматической настройки параметров интеллектуальных систем управления для технических объектов с априорной неопределенностью [11, 12]. Рассмотрим этапы реализации предлагаемого метода синтеза нечетких регуляторов, последовательность которых показана на рисунке 1.

Получение исходных данных входных и выходных сигналов управления в системе с классическим регулятором. Эти данные можно либо снять с реального объекта в процессе его функционирования, либо получить в процессе моделирования. В данной работе исследования выполнялись с помощью математической модели системы управления, разработанной в среде MatLab Simulink. Схема моделирования представлена на рисунке 2.

Схема моделирования содержит два одинаковых объекта управления, одним из которых управляет классический регулятор, а другим – нечеткий. На вход системы поступает задающее воздействие. Входные и выходные данные классического регулятора в процессе моделирования записываются в файл Base.mat.

Формирование кластеров и определение параметров функций принадлежности лингвистических переменных. В результате выполнения этапа 1 получены ряды данных Rd для входных и выходных сигналов классического регулятора. Для каждого ряда данных вводится лингвистическая переменная Lv, которая характеризуется набором áN, T, Xñ, где N – имя лингвистической переменной; T = {Ti} (i = {1, 2, …, m}) – терм-множество лингвистической переменной; X – область определения элементов из T (базовое множество).

Рассматриваемый метод синтеза нечеткого регулятора не предполагает привлечения экспертов, поэтому входные лингвистические переменные будем автоматически именовать Inp1, Inp2, …, InpM, а выходные – Out1, Out2, …, OutK в соответствии с количеством рядов данных.

Терм-множество лингвистической переменной также определим автоматически в виде T = {“1”, “2”, …, “m”} в соответствии с заданным количество термов.

Универсальное множество определяется из ряда данных, например, для входной лингвистической переменной InpI универсальное множество X = [min(Rd(InpI)), max(Rd(inpI))] = = [xiMin, xiMax].

Определим значения лингвистической переменной N из терм-множества T с помощью нечетких переменных Nv: Nv = áTi, X, miñ, где Ti – имя нечеткой переменной; mi – нечеткое множество.

В данной работе будем рассматривать тре- угольные функции принадлежности [13], описываемые формулой

         (1)

Как видно из (1), определения требуют параметры a, b, d для каждой функции принадлежности m. Допустим, что при i = 1 a = c, а при i = m b = d и точка пересечения соседних функций принадлежности m = 0,5, тогда терм-множество T будет иметь вид, представленный на рисунке 3.

Требуется данные из Rd поставить в соответствие элементам терм-множества T. Для этого выделим в универсальном множестве X кластеры cj Î С. Пусть количество кластеров определяется количеством термов в терм-множестве лингвистической переменной. Тогда размер кластера dc можно определить по фор- муле 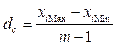, а интервалы кластеров по формулам:

Зная интервалы кластеров, нетрудно определить центры кластеров cd и параметры a, b, d функций принадлежности:

При использовании других функций принадлежности, например, трапециевидных [14] с

расчетные выражения будут иметь вид:

Для других видов функций принадлежности их параметры определяются по этому же принципу.

Создание базы правил. После определения параметров кластеров и функций принадлежности выполняется анализ Rd с целью определения принадлежности значений сигнала тому или иному кластеру. Для этого в циклах перебираются значения ряда данных и элементы множества C и определяется попадание данных в кластеры, как представлено на рисунке 4.

Для всех рядов данных определяется принадлежность кластерам и в несколько шагов формируется база правил.

Сначала таблицы кластеров всех входных и выходных переменных объединяются в единую, как представлено в таблице 1.

Таблица 1

Объединенная таблица кластеров

Table 1

Consolidated cluster table

Затем в ней выполняется поиск одинаковых строк, оставляется одна из них, а остальные удаляются, чтобы устранить дублирование правил.

Таким образом, на данном этапе формируется база правил. Следует иметь в виду, что она может быть недостаточной или избыточной. Недостаточность базы правил может быть обусловлена небольшой размерностью ряда исходных данных Rd или большим количеством термов лингвистических переменных, избыточность – наличием в таблице правил, у которых антецедент одинаковый, а консеквент разный. В этом случае потребуется редукция базы правил.

Редукция базы правил. Редукция базы правил направлена на устранение ее избыточности из-за правил с одинаковым антецедентом, но разным консеквентом. Рассмотрим процедуру редукции на примере.

Пусть у регулятора с тремя входными и одним выходным сигналами в таблице правил имеются избыточные правила, представленные в таблице 2.

Таблица 2

Избыточные правила в базе правил

Table 2

Redundant rules in the rule base

Находим центры кластеров консеквентов cm избыточных правил. Определяем среднее арифметическое:

,                                              (2)

где p – количество избыточных правил с одинаковым антецедентом.

Затем определяем принадлежность s кластеру из Cout и назначаем его номер консеквенту в одном из избыточных правил, а остальные удаляем. Следует отметить, что если избыточных правил два и их консеквенты соответствуют рядом расположенным термам, ис- пользование выражения (2) приводит к неопре- деленности. Для данного случая нужно ввести в терм-множество выходной лингвистической переменной дополнительный терм с параметрами (рис. 5): aj = cd(j–1), bj = s, dj = cd(j+1), где j – 1, j + 1 – центры кластеров, образующих функции принадлежности консеквентов избыточных правил.

Выполняя данную процедуру для всех наборов избыточных правил, получаем редуцированную базу правил.

Результаты моделирования

Исследование предложенного метода синтеза нечетких регуляторов выполнялось в среде MatLab в соответствии со схемой, приведенной на рисунке 2. В качестве объекта управления был выбран двигатель постоянного тока с математической моделью в виде передаточной функции: .

В качестве традиционного регулятора использовался ПИ-регулятор с параметрами KP = 0,221, KI = 1,1.

На вход системы подавался сигнал, изображенный на рисунке 6.

С его использованием был получен ряд данных c ПИ-регулятора, представленный в таблице 3.

Исследование выполнялось для входных лингвистических переменных с пятью термами и выходной с семью термами. Для каждого сигнала сгенерированы лингвистические переменные с параметрами:

Lv1 = á”Inp1”, {“1”, “2”, “3”, “4”, “5”}, [–0,29; 0,9]ñ;

Lv2 = á”Inp2”, {“1”, “2”, “3”, “4”, “5”}, [0,0; 0,0798]ñ;

Lv3 = á”Out”, {“1”, “2”, “3”, “4”, “5”, “6”, “7”}, [0,0108; 0,2089]ñ.

Определены следующие интервалы кластеров:

C1 = {[–0,2968; 0,0024], [–0,2968; 0,3016], [0,0024; 0,6008], [0,3016; 0,9], [0,6008; 0,9]};

C2 = {[0; 0,02], [0; 0,0399], [0,02; 0,0599],[0,0399; 0,0798], [0,0599; 0,0798]};

C3 = {[0,0108; 0,0438], [0,0108; 0,0768], [0,0438; 0,1099], [0,0768; 0,1429], [0,1099; 0,1759], [0,1429; 0,2089], [0,1759; 0,2089]}.

В результате кластеризации исходных данных составлена база правил, представленная в таблице 4.

В последнем столбце таблицы 4 указаны пять групп избыточных правил, следовательно, база правил требует редукции. В результате процедуры редукции, описанной выше, получена редуцированная база правил, представленная в таблице 5.

Как видно, полученная база правил не содержит избыточных правил. Следует отметить, что она неполная, так как должна содержать 25 правил. На основе полученных данных сгенерирована и открыта в FuzzyLogicToolbox среды MatLab fis-структура, параметры которой представлены на рисунке 7.

Как видно из результатов, автоматическая генерация нечеткого регулятора прошла успешно. Сгенерированная структура была подключена к схеме моделирования (рис. 2), и промоделирована вся система в целом. Результаты моделирования в сравнении нечеткого и ПИ-регулятора представлены на рисунке 8.

Таблица 4

База правил

Table 4

 Rule base

Таблица 5

Редуцированная база правил

Table 5

Reduced rule base

Обсуждение результатов

Результаты моделирования показали, что в случае синтеза регулятора с нередуцированной базой правил переходные процессы происходят с перерегулированием, особенно на первом этапе управления при входном воздействии 0,9. После редуцирования база правил сократилась с 17 до 12 правил. После редуцирования синтезированный нечеткий регулятор обеспечивает переходный процесс без перерегулирования и с меньшим временем регулирования по сравнению с классическим регулятором. Эксперименты авторов показали незначительное улучшение показателей качества управления при увеличении количества термов в терм-множествах лингвистических перемен- ных. Кроме того, при увеличении количества термов могут возникать ситуации, когда некоторые кластеры не содержат исходных данных и являются пустыми, то есть функции принадлежности, построенные на основе параметров пустых кластеров, априори не попадут в базу правил. Эксперименты с большими выборками исходных данных (2 000 и более значений для каждого входного сигнала) показали, что длительность синтеза нечеткого регулятора в среде MatLab составляет не более 10 секунд. Также следует отметить, что полученная база правил (табл. 5) является неполной и, следовательно, нечеткий регулятор будет эффективно функционировать при ступенчатом входном сигнале представленного на рисунке 5 типа. Для получения полной базы правил необходимо снимать исходные данные с системы управления для более разнообразного вход- ного сигнала, покрывающего все возможные сочетания функций принадлежности в антецедентах нечетких правил.

Заключение

Отличительной особенностью разработанного метода синтеза нечетких регуляторов является возможность автоматической генерации нечетких правил по измеренным данным из реальной системы управления или ее модели. В процессе синтеза экспертом задается только количество термов лингвистических переменных, а все остальные процедуры выполняются автоматически.

Рассчитанные интервалы кластеров пересчитываются в параметры функций принадлежности лингвистических переменных и позволяют выполнить анализ исходных данных для выявления принадлежности к тому или иному кластеру. Предложенная процедура редуцирования базы правил позволяет устранить избыточность и противоречивость данных.

Предлагаемый метод синтеза нечетких регуляторов может найти практическое применение:

-     как самостоятельный инструмент для автоматического создания нечетких регуляторов, при этом эксперты задействованы только на этапе задания вида функций принадлежности и количества термов в терм-множествах;

-     для помощи экспертам при создании нечетких баз правил, при этом эксперты имеют возможность расширить сгенерированную базу правил и дополнить ее недостающими правилами;

-     для исследования принципов управления техническими системами.

С использованием предложенного подхода нечеткие регуляторы синтезируются на основе алгоритма Мамдани, поэтому эксперт может изучать сгенерированную базу правил и разобраться с особенностями функционирования системы управления.

Достоинством предлагаемого подхода является то, что он позволяет формализовать и синтезировать нечеткие регуляторы на основе входных сигналов, которые являются трудноформализуемыми для экспертов. Например, эксперты легко могут синтезировать нечеткие регуляторы на основе сигналов ошибки и ее производной, но интеграл ошибки с трудом формализуется с привлечением экспертных знаний.

Будущие исследования авторов направлены на разработку алгоритма автоматического определения вида и количества функций принадлежности лингвистических переменных, а также на исследование методов кластеризации для кластеров с незаданными интервалами границ.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-38-00711.

Литература

1.    Kropotov D., Vetrov D. An algorithm for rule generation in fuzzy expert systems. Proc. ICPR, UK, Cambridge, 2004, vol. 1. DOI: 10.1109/ICPR.2004.1334061.

2.    Mohammed Al-S., Maysam F. Automatic generation of fuzzy classification rules using granulation-based adaptive clustering. Proc. IEEE Systems Conf., 2015. DOI: 10.1109/SYSCON.2015.7116825.

3.    Xiong N., Litz L. Reduction of fuzzy control rules by means of premise learning – method and case study. Proc. Fuzzy Sets and Systems, 2002, vol. 132, pp. 217–231.

4.    Nelles O. GA-based generation of fuzzy rules. Pedrycz W. (eds): Fuzzy Evolutionary Computation. Springer, 1997, pp. 269–295. DOI: 10.1007/978-1-4615-6135-4_12.

5.    Gegov A., Sanders D., Vatchova B. Aggregation of inconsistent rules for fuzzy rule base simplification. KES Journal, 2017, vol. 21, no. 3, pp. 135–145. DOI: 10.3233/KES-170358.

6.    Yung-Chou C., Li-Hui W., Shyi-Ming C. Generating weighted fuzzy rules from training data for dealing with the iris data classification problem. IJASE, 2006, vol. 4, no. 1, pp. 41–52.

7.    Castellano G., Fanelli A. A staged approach for generation and compression of fuzzy classification rules. FUZZ IEEE, Proc. Fuzzy Systems, 2000, vol. 1, pp. 42–47.

8.    Surmann H., Selenschtschikow A. Automatic generation of fuzzy logic rule bases: Examples I, Proc. ICSC, Cuba, 2002, pp. 75–81.

9.    Mohammed Al-S., Maysam F. Automatic generation of fuzzy classification rules from data. Proc. Recent Advances in Neural Networks and Fuzzy Systems, Italy, Venice, 2014, pp. 74–79.

10. García F., Martinez P., Paz V. Rule base reduction on a self-learning fuzzy controller. Proc. EUSFLAT-ESTYLF Joint Conf. 1999. URL: https://core.ac.uk/download/pdf/61893156.pdf (дата обращения: 19.08.2019).

11. Игнатьев В.В., Курейчик В.М., Спиридонов О.Б., Игнатьева А.С. Метод гибридного управления на основе адаптивной системы нейро-нечеткого вывода // Изв. ЮФУ. Технич. науки. 2017. № 9. С. 124–132.

12. Ignatyev V.V., Kovalev A.V., Spiridonov O.B., Ignatyeva A.S., Bozhich V.I., Boldyreff A.S. Model of adaptive system of neuro-fuzzy inference based on PI- and PI-fuzzy-controllers. Proc. SPIE Security, Berlin, Germany, 2018, vol. 10799 107990Y-1. DOI: 10.1117/12.2513302.

13. Yasin Md., Sultan A., Khodadad A. Comparison of fuzzy multiplication operation on triangular fuzzy number. IOSR-JM, 2016, vol. 12, iss. 4, pp. 35–41.

14. Rahmani A., Hosseinzadeh F., Rostamy-Malkhalifeh M., Allahviranloo T. A new method for defuzzification and ranking of fuzzy numbers based on the statistical beta distribution. Advances in Fuzzy Systems. 2016. DOI: 10.1155/2016/6945184.

References

1. Kropotov D., Vetrov D. An algorithm for rule generation in fuzzy expert systems. Proc. ICPR. UK, Cambridge, 2004, vol. 1. DOI: 10.1109/ICPR.2004.1334061.
2. Mohammed Al.S., Maysam F. Automatic generation of fuzzy classification rules using granulation-based adaptive clustering. Proc. IEEE SysCon. 2015. DOI: 10.1109/syscon.2015.7116825.
3. Xiong N., Litz L. Reduction of fuzzy control rules by means of premise learning – method and case study. Proc. Fuzzy Sets and Systems. 2002, vol. 132, pp. 217–231.
4. Nelles O. GA-based generation of fuzzy rules. Pedrycz W. (eds): Fuzzy Evolutionary Computation. Springer, 1997, pp. 269–295. DOI: 10.1007/978-1-4615-6135-4_12.
5. Gegov A., Sanders D., Vatchova B. Aggregation of inconsistent rules for fuzzy rule base simplification. KES Journal. 2017, vol. 21, no. 3, pp. 135–145. DOI: 10.3233/KES-170358.
6. Yung-Chou C., Li-Hui W., Shyi-Ming C. Generating weighted fuzzy rules from training data for dealing with the iris data classification problem. IJASE. 2006, vol. 4, no. 1, pp. 41–52.
7. Castellano G., Fanelli A. A staged approach for generation and compression of fuzzy classification rules. Proc. IEEE Fuzzy Systems. 2000, vol. 1, pp. 42–47.
8. Surmann H., Selenschtschikow A. Automatic generation of fuzzy logic rule bases: Examples I, Proc. ICSC. Cuba, 2002, pp. 75–81.

9. Mohammed Al.S., Maysam F. Automatic generation of fuzzy classification rules from data. Proc. Recent Advances in Neural Networks and Fuzzy Systems. Italy, Venice, 2014, pp. 74–79.

10. García F., Martinez P., Paz V. Rule base reduction on a self-learning fuzzy controller. Proc. EUSFLAT-ESTYLF Joint Conf. 1999. Available at: https://core.ac.uk/download/pdf/61893156.pdf (accessed August 19, 2019).

11. Ignatyev V.V., Kureychik V.M., Spiridonov O.B., Ignatyeva A.S. Hybrid control method based on an adaptive neuro-fuzzy inference system. Proc. SFedU. Eng. Sci. Taganrog, 2017, no. 9, pp. 124–132 (in Russ.).
12. Ignatyev V.V., Kovalev A.V., Spiridonov O.B., Ignatyeva A.S., Bozhich V.I., Boldyreff A.S. Model of adaptive system of neuro-fuzzy inference based on PI- and PI-fuzzy-controllers. Proc. SPIE Security. Berlin, Germany, 2018, vol. 10799 107990Y-1. DOI: 10.1117/12.2513302.
13. Yasin Md., Sultan A., Khodadad A. Comparison of fuzzy multiplication operation on triangular fuzzy number. IOSR-JM. 2016, vol. 12, iss. 4, pp. 35–41.
14. Rahmani A., Hosseinzadeh F., Rostamy-Malkhalifeh M., Allahviranloo T. A new method for defuzzification and ranking of fuzzy numbers based on the statistical beta distribution. Advances in Fuzzy Systems. 2016. DOI: 10.1155/2016/6945184.