Программные продукты и системы

Основная идея технологии генерации поисковых запросов, фильтрации и ранжирования результатов поиска – организация с помощью специального генетического алгоритма (ГА) эволюционного процесса (ГАП), формирующего в поисковой системе устойчивую и эффективную популяцию запросов для получения высокорелевантных результатов. Специальным образом закодированные запросы последовательно подвергаются генетическим изменениям и выполняются в поисковой системе. Оценивается релевантность промежуточных результатов поиска, вычисляются значения (целевой) фитнес-функции и осуществляется отбор наиболее пригодных запросов. Процесс повторяется до достижения квазиоптимального значения фитнес-функции.

Значение фитнес-функции ГАП определяет качество поисковых запросов и вычисляется для каждого найденного документа в результате выполнения запроса. Это значение зависит от следующих факторов: позиция документа в ранжированном списке результатов запроса, вхождение данного документа в списки результатов других запросов, семантическая близость к адаптивно модифицируемому исходному набору ключевых термов – поисковому паттерну.

В настоящей статье описываются результаты исследования способов аналитического определения веса каждого фактора, влияющего на значение фитнес-функции, и сравнительного анализа применимости каждого способа для оценки динамики изменения значений фит- нес-функции ГАП.

Описание ГАП и его фитнес-функции

В работах [1, 2] отмечается, что в ГАП поисковый паттерн K для документов есть набор термов, относящихся к некоторой предметной области. Каждый поисковый запрос представлен вектором  = (c1, c2, …, cn, …, cm), где cn = {kn, wn, Sn}, kn Î K – терм; wn – вес терма; Sn – множество синонимов терма kn; m – количество термов в запросе. Результат выполнения запроса – это набор документов R, ½R½ = D. Исходная популяция из N поисковых запросов представлена множеством Q0, где ½Q0½ = N, N < ½K½/2,  Î Q0. Результатом поискового запроса является множество документов R, которое формируется после выполнения  в поисковой системе (Bing, Google, БД SQL, данные в структуре XML и т.п.).

Эволюционная операция скрещивания (одно- или двухточечный кроссовер) реализуется обменом термами между запросами, то есть компонентами векторов  для репродукции запросов используется генотипный аутбридинг. Адекватная операция мутации – это вероятностная замена синонимом k’n Î Sn  случайно выбранного терма запроса kn. При формировании новой популяции запросов используется элитарный отбор. Условием остановки алгоритма в общем случае считается стабильность популяции.

Значение фитнес-функции, или функции пригодности  определяет качество запросов; ГАП ищет максимум

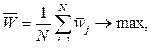                                (1)

где  – фитнес-функция j-го запроса популяции,

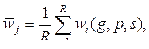                               (2)

где wi – фитнес-функция для i-го результата j-го запроса – результата ri имеет вид аддитивного критерия оптимальности:

wi = wgg + wpp + wss.                                (3)

Значение g учитывает ранг для ri, установленный поисковой системой:

, ,    (4)

где  – номер позиции ri в ранжированном списке результатов j-го запроса популяции; gmax, gmin – наибольшее и наименьшее значения g(ri, R) среди всех результатов запросов популяции.

Значение p учитывает универсальность ri, то есть частоту появления ri в списках результатов других запросов. Оно определяется следующим образом:

, ,      (5)

где , если ri присутствует в списке результатов j-го запроса, иначе ; pmax, pmin – наибольшее и наименьшее значения p(ri, R) среди всех результатов запросов популяции.

Значение s определяет семантическую близость ri и поискового образа K. В работе используется косинусная мера близости векторов документов, как это принято в векторной модели пространства документов [3]. Таким образом,

,                           (6)

где  – вектор i-го результата запроса, T – количество термов в тексте результата запроса после морфологического анализа (принимаются во внимание только существительные и прилагательные) и лемматизации (в качестве текста результата используются заголовок документа и его краткое описание (сниппет)),  – вес i-го терма из текста результата запроса,  – частота использования термина в этом тексте, , Rn – число результатов, текст которых содержит n-й терм i-го результата;  – вектор поискового образа документов K,  – вес m-го терма из K, , Rm – число результатов, текст которых содержит m-й терм из K; wg, wp, ws – весовые коэффициенты для g, p, s соответственно.

Способы аналитического определения весовых коэффициентов

Как уже отмечалось, задачей являлось исследование способов аналитического определения веса (или значимости) каждого фактора, влияющего на значение фитнес-функции. То есть необходимо определить значения весовых коэффициентов wg, wp и ws для факторных переменных g, p и s в соответствии с (3).

Отметим, что метод взвешенной суммы критериев основан на свертывании всех крите- риев в единственный обобщенный (глобальный, интегральный, агрегированный и т.д.) критерий, представляющий собой сумму критериев, взвешенных коэффициентами их относительной важности, или весами [4]. Метод известен давно, однако до сих пор является довольно распространенным и чаще других используется и активно совершенствуется [5, 6].

Оценка значений весовых коэффициентов с использованием экспертных методов включает следующие основные этапы: определение цели, формирование группы экспертов, разработка сценария и процедур экспертизы, сбор и анализ экспертной информации, анализ результатов экспертизы. Очевидно, что в рассматриваемом случае даже хорошо обоснованные экспертные методы [7] не подходят. Основная причина в отсутствии критериев для совместной сравнительной оценки факторов экспертами. Поэтому разумным представляется принять, что wg = wp = ws.

Рассмотрим некоторые способы и приемы, позволяющие по информации о качестве значений факторных переменных определять значения весовых коэффициентов wk [8, 9].

Способ 1. Для каждого частного критерия Fk(X) > 0, k = 1, 2, …, c, вычисляется коэффициент относительного разброса dk, который определяет максимально возможное отклонение по k-му частному критерию:

,                            (7)

где 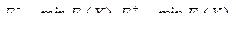 Весовые коэффициенты wk получают наибольшее значение для тех критериев, относительный разброс которых в области оценок наиболее значительный:

                                     (8)

Способ 2. Пусть все  тогда можно рассмотреть отклонение частного критерия от его наименьшего значения:

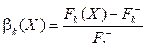.                               (9)

Предположим, что важность k-го критерия зависит от выполнения неравенства

                                           (10)

Величины xk задаются из условия, что, чем важнее критерий, тем меньшее значение xk выбирается. Геометрическая интерпретация выполнения неравенства (10) будет следующей. Пусть  – наибольший радиус шара, постро- енного около точки минимума  для критерия Fk(X), внутри которого точки  удовлетворяют условию (10). Тогда

.                     (11)

Очевидно, что, чем больше радиус шара  в котором относительное отклонение k-го критерия от его минимального значения не превосходит xk, тем меньшее значение весового коэффициента wk надо выбирать:

.                                (12)

Также имеются оригинальные разработки методов определения весовых коэффициентов, основанные на эвристических алгоритмах [10].

Методика проведения исследований

Для вычисления весовых коэффициентов описанными выше способами использовались результаты экспериментов с ГАП, выполненных ранее (https://www.rfbr.ru/rffi/ru/project_ search/o_2071601). Исходный набор K был сформирован из терминов предметной области, касающейся управления эволюцией технологических процессов на промышленных предприятиях. Использовались поисковая система Bing и следующий исходный набор значений основных параметров:

-     количество запросов в генерируемых популяциях K = 5;

-     количество ключевых слов в каждом генерируемом запросе M = 8;

-     максимальное количество результатов поиска, возвращаемых запросом Rq = 20, либо популяцией запросов RQ = 20, либо суммарно всеми популяциями R = 20;

-     вероятность мутации запроса pm = 0,1;

-     число проходов алгоритма (или число генерируемых популяций) NQ = 200.

Отметим, что условие остановки алгоритма при проведении экспериментов было отменено для создания условий предотвращения преждевременной сходимости ГАП.

Фрагмент исходных данных в качестве примера представлен в таблице.

Весовые коэффициенты wg, wp и ws необходимо вычислить способами 1 и 2. Причем вычисления должны быть произведены для следующих диапазонов исходных данных:

-     результаты выполнения каждого запроса популяции, 1 £ ri £ Rq;

-     результаты выполнения запросов каждой популяции,

-     результаты выполнения запросов всех популяций,

Фрагмент исходных данных

Source data chunk

Порядок вычислений значений весовых коэффициентов по способу 1 (пример). В качестве исходных примем данные из таблицы. Коэффициенты относительного разброса для частных критериев следующие:

dg = 1 – (0,43/0,95) = 0,5474,

dp = 1 – (0,13/1,00) = 0,8700,

ds = 1 – (0,05/0,09) = 0,4444.

Тогда весовые коэффициенты примут следующие значения:

wg = 0,5474/(0,5474 + 0,8700 + 0,4444) = 0,294,

wp = 0,8700/(0,5474 + 0,8700 + 0,4444) = 0,467,

ws = 0,4444/(0,5474 + 0,8700 + 0,4444) = 0,239.

Отметим, что wg + wp + ws = 1.

Порядок вычислений значений весовых коэффициентов по способу 2 (пример). В качестве исходных данных также примем исходные данные из таблицы. Пусть xg = 33, xp = 33, xs = 34. Тогда, в соответствии с (10):

bg = (F(g) – 0,43)/0,43 £ 0,33 при F(g) £ 0,4719,

bp = (F(p) – 0,13)/0,13 £ 0,33 при F(g) £ 0,3729,

bs = (F(s) – 0,42)/0,42 £ 0,32 при F(g) £ 0,4828.

Следовательно:

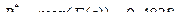
Тогда весовые коэффициенты примут следующие значения:

wg = 0,4719/(0,4719 + 0,3729 + 0,4828) = 0,355,

wp = 0,3729/(0,4719 + 0,3729 + 0,4828) = 0,281,

ws = 0,4828/(0,4719 + 0,3729 + 0,4828) = 0,364.

Отметим, что wg + wp + ws = 1.

Вычисленные значения весовых коэффициентов wg, wp и ws = 1, а также весовые коэффициенты для случая wg = wp = ws должны быть использованы для вычисления фитнес-функции  Далее должен быть проведен сравнительный анализ поведения функции при выполнении ГАП с исходным набором K.

Результаты исследований

На рисунке 1 представлены графики зависимости значений фитнес-функции  от номеров популяций запросов, порожденных ГАП. Вычисление  производилось для документов из диапазона , где ri – номер i-го документа в результатах выполнения запросов всех популяций.

На рисунке 2 изображены графики зависимости значений фитнес-функции  от номеров первых 30 популяций запросов, порожденных ГАП. Вычисление  производилось для документов из диапазона .

На рисунке 3 приведены графики зависимости значений фитнес-функции  от номеров первых 10 популяций запросов, порожденных ГАП. Вычисление  производилось для документов из диапазона 1 £ ri £ Rq.

Во всех случаях весовые коэффициенты wg, wp и ws принимались равными друг другу, а также вычислялись описанными выше способами 1 и 2. Соответственно, на графиках использованы следующие обозначения фитнес-функции: Wequ при wg = wp = ws; Wdis при вычислении wg, wp и ws способом 1; Wrad при вычислении wg, wp и ws способом 2.

Обсуждение результатов

Полученные результаты экспериментов позволяют отметить некоторые особенности фитнес-функции ГАП с весовыми коэффициентами, вычисленными различными способами, а также сделать ряд предположений.

1. Как следует из рисунка 1, графики фитнес-функций Wequ, Wdis и Wrad, значения которых вычислены по результатам выполнения за- просов всех популяций, в большой степени по- хожи. Можно предположить, что Wrad = Wequ + + dequ и Wrad = Wdis + ddis, причем ddis > dequ  и , где  и R(d) – области значений  и d соответственно. На всех трех графиках отчетливо видны локальный и глобальный максимумы  достигаемые практически в одних и тех же точках. В целом при данном диапазоне исходных данных ни один из предложенных способов расчета весовых коэффициентов не дает очевидных преимуществ.

2. При анализе графика функции Wrad на рисунке 2 можно увидеть, что при работе ГАП на заданной области определения Wrad отчетливо видны два локальных максимума, причем первый из них достигается достаточно быстро (в пределах 10 популяций). Также можно видеть последовательные улучшения популяций запросов, характерные для корректной работы генетических алгоритмов. На графиках функций Wequ и Wdis подобного не наблюдается: точка первого локального максимума пропущена, точка второго локального максимума совпадает с аналогичной точкой для Wrad, но сам максимум менее выражен. Вывод – расчет весовых коэффициентов по способу 2 с использованием результатов выполнения запросов каждой популяции представляется более предпочтительным.

3. Графики фитнес-функций Wequ, Wdis и Wrad показывают наличие локальных максимумов, найденных ГАП. Однако точки максимумов различны для всех вариантов  Из-за небольшого количества шагов выполнения ГАП формулировка каких-либо выводов для данного диапазона исходных данных, используемого при расчете весовых коэффициентов, пока преждевременна.

Заключение

Результаты экспериментов позволяют сделать вывод об эффективности предложенного подхода. Показано, как метод определения весовых коэффициентов для аддитивного критерия оптимальности – фитнес-функции ГАП – может повысить качество работы генетического алгоритма для формирования эффективных поисковых запросов. В частности, повышается вероятность быстрого обнаружения локальных экстремумов фитнес-функции, которые на заданной области ее определения могут стать оптимальным решением.

Результаты исследования будут использованы при разработке механизма селекции информации об инновационных объектах, основанного на определении семантической релевантности такой информации генерируемым поисковым запросам. Механизм является частью технологии хранилища данных с автоматическим пополнением данными из различных источников.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-00358 А.

Литература

1.    Ivanov V.K., Palyukh B.V., Sotnikov A.N. Efficiency of genetic algorithm for subject search queries. Lobachevskii J. of Mathematics, 2016, vol. 12, no. 3, pp. 244–254.

2.    Иванов В.К., Мескин П.И. Реализация генетического алгоритма для эффективного документального тематического поиска // Программные продукты и системы. 2014. № 4. С. 118–126. DOI: 10.15827/0236-235X.108.118-126.

3.    Salton G., Wong A., Yang C.S. A vector space model for automatic indexing. Communications of the ACM, 1975, vol. 18, pp. 613–620.

4.    Подиновский В.В., Потапов М.А. Метод взвешенной суммы критериев в анализе многокритериальных решений: Pro et contra // Бизнес-информатика. 2013. № 3. С. 41–48.

5.    Подиновский В.В. Чувствительность многокритериального выбора к изменению оценок важности неоднородных критериев // ИТНОУ. 2017. № 4. С. 23–27.

6.    Sorooshian S., Parsia Y. Modified weighted sum method for decisions with altered sources of information. Mathematics and Statistics, 2019, vol. 7, no. 3, pp. 57–60. URL: http://www.hrpub.org/download/20190630/MS1-13412797.pdf (дата обращения: 10.12.2019). DOI: 10.13189/ms.2019.070301.

7.    Спиридонов С.Б., Булатова И.Г., Постников В.М. Анализ подходов к выбору весовых коэффициентов критериев методом парного сравнения критериев // Науковедение. 2017. Т. 9. № 6. URL: https://naukovedenie.ru/PDF/16TVN617.pdf (дата обращения: 10.12.2019).

8.    Гудков П.А. Методы сравнительного анализа. Пенза, 2008. 81 с.

9.    Карпушкин С.В. Теория принятия проектных решений. Тамбов: Изд-во ТГТУ, 2015. 86 с.

10. Al-Shargabi B., Sabri O., Aljawarneh Sh. An enhanced arabic information retrieval using genetic algorithms: an experimental study and results. Aust. J. Basic & Appl. Sci., 2013, vol. 7, no. 13, pp. 242–248.

References

1. Ivanov V.K., Palyukh B.V., Sotnikov A.N. Efficiency of genetic algorithm for subject search queries. Lobachevskii J. of Mathematics. 2016, vol. 12, no. 3, pp. 244–254.
2. Ivanov V.K., Meskin P.I. Genetic algorithm implementation for effective document subject search. Software & Systems. 2014, no. 4, pp. 118–126. DOI: 10.15827/0236-235X.108.118-126 (in Russ.).
3. Salton G., Wong A., Yang C.S. A vector space model for automatic indexing. Communications of the ACM. 1975, vol. 18, pp. 613–620.
4. Podinovsky V.V., Potapov M.A. Weighted sum method in the analysis of multicriterial decisions: pro et contra. Business Informatics. 2013, no. 3, pp. 41–48 (in Russ.).
5. Podinovsky V.V. Sensitivity of multi-criterial selection to change assessment assessments of inhomogeneous criteria. ITNOU. 2017, no. 4, pp. 23–27 (in Russ.).
6. Sorooshian S., Parsia Y. Modified weighted sum method for decisions with altered sources of information. Mathematics and Statistics. 2019, vol. 7, no. 3, pp. 57–60. Available at: http://www.hrpub.org/download/20190630/MS1-13412797.pdf (accessed December, 10, 2019). DOI: 10.13189/ms.2019.070301.
7. Spiridonov S.B., Bulatova I.G., Postnikov V.M. Analysis of approaches to the choice of weighting criteria method of pair comparison of criteria. Int. J. Naukovedenie. 2017, vol. 9, no. 6. Available at: https://naukovedenie.ru/PDF/16TVN617.pdf (accessed December, 10, 2019) (in Russ.).
8. Gudkov P.A. Benchmarking Methods. Penza, 2008, 81 p.
9. Karpushkin S.V. Decision Theory. Tambov, TSTU Publ., 2015, 86 p. (in Russ.).
10. Al-Shargabi B., Sabri O., Aljawarneh Sh. An enhanced arabic information retrieval using genetic algorithms: an experimental study and results. Aust. J. Basic & Appl. Sci. 2013, vol. 7, no. 13, pp. 242–248.