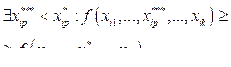Одним из вариантов практического применения алгоритмов машинного обучения является решение задачи классификации объек- тов [1]. Каждый объект данных представляется как вектор (точка) в p-мерном пространстве (упорядоченный набор p чисел). Каждая из этих точек принадлежит одному из двух классов. Необходимо определить, возможно ли разделение точек гиперплоскостью размерности p – 1, то есть, являются ли эти два класса линейно разделимыми. Искомых гиперплоскостей может быть много, поэтому полагают, что максимизация зазора между классами способствует более точной классификации. Необходимо найти такую гиперплоскость, чтобы расстояние от нее до ближайшей точки было мак- симальным. Это эквивалентно тому, что сумма расстояний до гиперплоскости от двух ближайших к ней точек, лежащих по разные стороны от нее, максимальна. Если такая гиперплоскость существует, она называется оптимальной разделяющей гиперплоскостью, а соответствующий ей линейный классификатор – оптимально разделяющим классификатором. Поиск данной гиперплоскости осуществляется с помощью алгоритма метода опорных векторов SVM (support vector machine) [2].
Метод SVM – это алгоритм обучения с учителем, используемый для решения задач классификации [3]. Его основная идея – перевод исходных векторов в пространство более высокой размерности (спрямляющее пространство) для обеспечения линейной разделимости классов и поиск разделяющей гиперплоскости с максимальным зазором в этом пространстве. Алгоритм работает в предположении, что, чем больше разница или расстояние между этими параллельными гиперплоскостями, тем меньше средняя ошибка классификатора.
Постановка задачи классификации
Определим точки обучающей выборки следующим образом: {(x1, ci), (x2, c2), …, (xn, cn)}, где ci принимает значение 1 или −1 в зависимости от того, к какому классу принадлежит точка xi [4]. Каждое xi – это p-мерный вещественный вектор, обычно нормализованный значениями [0, 1] или [−1, 1]. Если точки не будут нормализованы, то точка с большими отклонениями от средних значений координат точек слишком сильно повлияет на классификатор. В обучающей выборке для каждого элемента задан класс, к которому он принадлежит. Необходимо, чтобы алгоритм метода опорных векторов классифицировал их таким же образом. Для этого строится разделяющая гиперплоскость, имеющая вид wx – b = 0.
Вектор w – перпендикуляр к разделяющей гиперплоскости. Параметр равен по модулю расстоянию от гиперплоскости до начала координат. Если параметр b равен нулю, гиперплоскость проходит через начало координат, что ограничивает решение.
равен по модулю расстоянию от гиперплоскости до начала координат. Если параметр b равен нулю, гиперплоскость проходит через начало координат, что ограничивает решение.
Так как необходимо найти оптимальное разделение, следует определить опорные векторы и гиперплоскости, параллельные оптимальной и ближайшие к опорным векторам двух классов. Можно показать, что эти параллельные гиперплоскости могут быть описаны следующими уравнениями (с точностью до нормировки): wx – b = 1, wx – b = –1.
Если обучающая выборка линейно разделима, то можно выбрать гиперплоскости таким образом, чтобы между ними не лежала ни одна точка обучающей выборки, а затем максимизировать расстояние между гиперплоскостями. Ширина полосы между ними равна 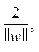 таким образом, поставленная задача сводится к минимизации úçwúç. Чтобы исключить все точки из полосы, необходимо убедиться, что для всех i
таким образом, поставленная задача сводится к минимизации úçwúç. Чтобы исключить все точки из полосы, необходимо убедиться, что для всех i

Указанные соотношения могут быть также записаны в виде
ci(wx – b ³ 1), 1 £ i £ n. (1)
Метод опорных векторов (SVM)
Основная идея метода SVM заключается в классификации объектов с помощью перевода исходных векторов, описывающих объекты, в пространство более высокой размерности и в поиске разделяющей гиперплоскости с максимальным зазором в этом пространстве. Две параллельные гиперплоскости строятся по обеим сторонам гиперплоскости, разделяющей классы. Это будет гиперплоскость, максимизирующая расстояние до двух параллельных гиперплоскостей. Алгоритм работает в предположении, что, чем больше разница или расстояние между этими параллельными гиперплоскостями, тем меньше средняя ошибка классификатора [5].
Случай линейной разделимости. Проблема построения оптимальной разделяющей гиперплоскости сводится к минимизации úçwúç при условии (1). Это задача квадратичной оптимизации, имеющая вид
 (2)
(2)
По теореме Куна–Таккера эта задача эквивалентна двойственной задаче поиска седловой точки функции Лагранжа:

где λ = (λ1, …, λn) – вектор двойственных переменных.
Задача сводится к эквивалентной задаче квадратичного программирования, содержащей только двойственные переменные:
 (3)
(3)
После решения данной задачи w и b можно найти по формулам: 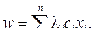 b = wxi – ci, li > 0.
b = wxi – ci, li > 0.
В итоге алгоритм классификации может быть записан в виде
 . (4)
. (4)
В данном случае суммирование идет только по опорным векторам, для которых λi ≠ 0, а не по всей выборке.
Случай линейной неразделимости. Для работы алгоритма в случае, если классы линейно неразделимы, следует допустить ошибку классификации на обучающей выборке. Вводится набор дополнительных переменных ξi ≥ 0, характеризующих величину ошибки на объектах xi, 1 £ i £ n. В качестве основы используется постановка задачи (2). В данные неравенства вводятся погрешность классификации, а также штраф за суммарную ошибку в минимизируемый функционал:

Коэффициент C – параметр настройки метода, который позволяет регулировать отношение между максимизацией ширины разделяющей полосы и минимизацией суммарной ошибки.
Аналогично по теореме Куна–Таккера задача сводится к поиску седловой точки функции Лагранжа:

Данная задача аналогично сводится к эквивалентной:
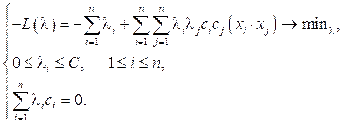
На практике при работе SVM решают именно эту задачу, а не (3), так как гарантировать линейную разделимость точек на два класса в общем случае не представляется воз- можным. Данный алгоритм называется алгоритмом с мягким зазором (soft-margin SVM). В случае линейной разделимости точек алгоритм называется алгоритмом с жестким зазором (hard-margin SVM).
Для алгоритма классификации сохраняется формула (4), однако теперь ненулевыми λi обладают не только опорные, но и неверно классифицированные объекты. В определенном смысле это недостаток, поскольку нарушителями часто оказываются шумовые выбросы и построенное на них решающее правило по сути опирается на шум. Константу C обычно выбирают по критерию скользящего контроля. При каждом значении C задачу приходится решать заново, что повышает трудоемкость работы алгоритма. Если есть основания полагать, что выборка почти линейно разделима и лишь объекты-выбросы классифицируются неверно, то можно применить фильтрацию выбросов. В этом случае вначале задача решается при некотором C и из выборки удаляется небольшая доля объектов, имеющих наибольшую величину ошибки ei. После этого задача решается заново по усеченной выборке. Вероятно, что для решения задачи будет необходимо проделать несколько таких итераций, пока оставшиеся объекты выборки не окажутся линейно разделимыми.
Ядра. Для ускорения работы метода SVM существует способ создания нелинейного классификатора, в основе которого лежит переход от скалярных произведений к произвольным ядрам, так называемый kernel trick, позволяющий строить нелинейные разделители [6]. Отличием данного алгоритма является то, что каждое скалярное произведение в приведенных выше формулах заменяется нелинейной функцией ядра (скалярным произведением в пространстве с большей размерностью). В этом пространстве уже может существовать оптимальная разделяющая гиперплоскость. Так как размерность получаемого пространства может быть больше размерности исходного, то преобразование, сопоставляющее скалярные произведения, будет нелинейным, а значит, функция, соответствующая в исходном пространстве оптимальной разделяющей гиперплоскости, также будет нелинейной. Необходимо отметить: если исходное пространство имеет достаточно высокую размерность, то велика вероятность, что выборка в нем окажется линейно разделимой [7].
Особенности SVM.
Преимущества:
- SVM является наиболее быстрым методом нахождения решающих функций;
- метод сводится к решению задачи квадратичного программирования в выпуклой области, всегда имеющей единственное решение;
- метод находит разделяющую полосу максимальной ширины, что в дальнейшем позволяет осуществлять более уверенную классификацию.
Недостатки:
- метод чувствителен к шумам и стандартизации данных;
- не существует общего подхода к автоматическому выбору ядра (и построению спрямляющего подпространства в целом) в случае линейной неразделимости классов;
- метод имеет высокую вычислительную сложность [8].
Метод FS-SVM – модификация метода SVM
Актуальность. Необходимо отметить, что работа алгоритма опорных векторов в общем случае связана с громоздкими вычислениями, что может привести к неоправданно высоким вычислительным затратам (поиск седловой точки функции Лагранжа, применение метода ядра и т.д.). Также существенным недостатком метода SVM является отсутствие общего подхода к автоматическому выбору ядра и построению спрямляющего подпространства в целом в случае линейной неразделимости классов.
В связи с этим необходима модификация метода опорных векторов, позволяющая обеспечить высокую точность решения задачи классификации (как и стандартный метод SVM в нелинейном случае с использованием функции ядра) и имеющая меньшую вычислительную и алгоритмическую сложность.
Для этого предлагается наложить некоторые ограничения на рассматриваемую задачу, что позволит разработать и применить модифицированный метод опорных векторов.
Функциональная разделимость классов. В качестве ограничения следует принять рассмотрение не общей задачи классификации классов произвольной формы, а задачи классификации при условии функционально разделимых классов.
Определение 1. Функциональная разделимость классов.
Классы являются функционально раздели- мыми, если существует функциональная зави- симость между каждым выходным параметром и набором входных параметров. При этом данная функция является непрерывной и монотонной на множестве значений входных параметров.
Формальное определение:
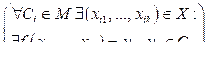 ,
,
&
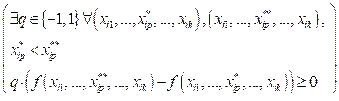 ,
,
где M – множество классов; Ci – i-й класс из m классов; X – множество n входных параметров; (xi1, …, xik) – подмножество k входных параметров, 1 £ k £ n; yi – значение функции; R = {³, £}, 1 £ p £ k.
 Данное определение проиллюстрировано на рисунке 1.
Данное определение проиллюстрировано на рисунке 1.
В качестве определения функциональной разделимости классов также можно рассматривать следующее.
Определение 2. Функциональная разделимость классов.
Классы являются функционально разделимыми, если существует функциональная зависимость между каждым выходным параметром и набором входных параметров. При этом производная данной функции не меняет знак или не определена в некоторых точках на множестве значений входных параметров.
Формальное определение:
 ,
,
&

Производная функции f ¢может оказаться неопределенной в случае, если функциональная зависимость f между входными и выходными параметрами будет представлена кусочной функцией. Тогда в точках излома данной функции производная будет не определена. Таких точек будет конечное множество, поскольку обучающая выборка, по которой может быть построена функция, является конечной последовательностью объектов, следовательно, и количество изломов может оказаться конечным.
Функциональная разделимость классов и выпуклые классы. В качестве ограничения, накладываемого на задачу классификации, также может рассматриваться условие выпуклости классов, однако оно является более жестким, чем условие функциональной разделимости (рис. 2).
Определение.
Множество M Ì Rd выпукло, если для любых точек A, B Î M отрезок AB лежит в M.

 На рисунке 3 представлено отличие данных условий.
На рисунке 3 представлено отличие данных условий.
При условии выполнимости ограничения функциональной разделимости классов для рассматриваемой задачи исключаются случаи, представленные на рисунке 3в, при которых в одной из проекций выходных переменных на множество входных переменных возможна ситуация включения одного класса в другой.
Описание блоков алгоритма FS-SVM. Рассмотрим подробно работу модифицированного метода опорных векторов – Functionally Separable – Support Vector Machine (FS-SVM).
Алгоритм FS-SVM состоит из следующих блоков.
1. Поиск опорных элементов, то есть элементов классов, которые находятся на границе класса (рис. 4а).
1.1. Элементы упорядочиваются по одной из координат при фиксированных значениях другой координаты.
 1.2. Пара элементов, для которых значение класса переходит с Ci на Cj, отмечаются как опорные элементы.
1.2. Пара элементов, для которых значение класса переходит с Ci на Cj, отмечаются как опорные элементы.
1.3. Процедура повторяется для оставшихся координат элементов.
2. Поиск точек для разделяющей гиперповерхности (рис. 4б).
2.1. Вычисляются векторы, соединяющие опорные элементы каждого класса.
2.2. Для каждого элемента класса Ci определяется элемент класса Cj, для которого расстояние до рассматриваемого элемента Ci будет минимальным.
2.3. Вычисляется середина вектора, соединяющего данные опорные элементы классов Ci и Cj. Полученная точка определяется как точка, через которую должна будет проходить разделяющая гиперповерхность.
2.4. Указанная процедура повторяется для всех опорных элементов классов Ci и Cj.
3. Построение разделяющей гиперповерхности как кусочно-линейной функции в проекции на рассматриваемые оси координат (рис. 4в). В дальнейшем развитии алгоритма указанную функцию можно аппроксимировать многочленом Чебышева для получения гладкой кривой (рис. 4г).
 При выполнении алгоритма осуществляются проверка контролируемых параметров и определение стороны относительно разделяющей гиперповерхности, в которой они находятся, для получения результата классификации.
При выполнении алгоритма осуществляются проверка контролируемых параметров и определение стороны относительно разделяющей гиперповерхности, в которой они находятся, для получения результата классификации.
Условие применимости метода FS-SVM. Необходимо отметить, что принципиальным ограничением данного алгоритма является необходимость выполнения условия, что все элементы класса должны находиться с одной из сторон от разделяющей функции (недопустимы случаи, представленные на рисунке 3в).
Докажем следующую теорему.
Теорема (FS).
В случае выполнения условия функциональной разделимости классов возможно применение модифицированного метода опорных векторов FS-SVM.
Доказательство.
Согласно определению функциональной разделимости классов, существует функциональная зависимость f между наборами исходных данных и результирующими данными задачи. Данная зависимость непрерывна и монотонна.
Монотонность функции f означает, что производная данной функции не меняет знак на об- ласти определения набора входных параметров.
Следовательно, пересечение данной гиперповерхности f пространством наборов исходных данных всегда будет представлять собой кривую незамкнутую линию.
Рассмотрим любую проекцию функциональной зависимости f на набор данных x. Тогда из условия монотонности следует, что она пересечет любой построенный перпендикуляр на ось Y не более одного раза: в случае строгой монотонности в точке или в случае нестрогой монотонности на отрезке.
Рассмотрим эту лемму.
Лемма (FS).

 Монотонная функция f пересекает поверхность не более одного раза: в случае строгой монотонности в точке или в случае нестрогой монотонности на отрезке (рис. 5).
Монотонная функция f пересекает поверхность не более одного раза: в случае строгой монотонности в точке или в случае нестрогой монотонности на отрезке (рис. 5).
Доказательство.
Функция f(x) непрерывна, то есть
"y $(xi1, …, xik): y = f(xi1, …, xik).
Функция f(x) монотонна:

Зафиксируем q = 1, то есть допустим, что функция f не убывает. Для q = –1 доказательство проводится аналогично:

Проведем доказательство от противного. Допустим, что
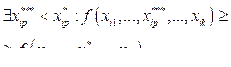
Однако, если 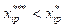 , то
, то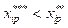 , тогда по определению
, тогда по определению

Поскольку , в предыдущей формуле заменим
, в предыдущей формуле заменим  на
на  . Получим:
. Получим:
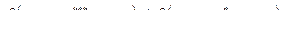
Получено противоречие предположению доказательства. Следовательно, верно обратное утверждение. Аналогично проводится доказательство для  .
.
Теорема Больцано–Коши о промежуточном значении. Пусть функция f непрерывна на отрезке [a, b] и C – произвольное число, находящееся между значениями функции на концах отрезка: A = f(a) и B = f(b). Тогда существует точка z Î [a, b], для которой f(z) = C.
Пусть для  ,
,  и
и .
.
Тогда по теореме Больцано–Коши о промежуточном значении получим, что

В данном случае C – неопределенность значения класса.
Лемма доказана.
Таким образом, можно расширить вывод леммы FS на каждый параметр xik, тогда

Поскольку функция f является разделительной между классами и незамкнутой, можно определить, с какой стороны от функции лежит конкретный пример из обучающей выборки, а значит, применить алгоритм FS-SVM.
Теорема доказана.
Практическое применение метода FS-SVM. Задача классификации режимов течения нефте-водо-газового потока.
Рассмотренное ограничение функциональной разделимости классов не является критическим для большого количества задач. В частности, это условие будет верно для задач, в которых исходные данные получены в результате наблюдения физических явлений с установленной монотонностью их происхождения.
Одной из таких задач является определение режимов течения нефте-водо-газового потока. Рассмотрим ее более подробно.
Нефтяное месторождение состоит из набора кустов скважин, каждый из которых содержит порядка десяти нефтедобывающих скважин, имеющих свои физические характеристики (плотность нефти, средние значения дебита продукции, количество примесей и другие). На нефтяных скважинах установлены насосы различных типов и производительности.
При добыче нефти происходит одновременная добыча нефти, воды, содержащейся в пласте, и попутно нефтяного газа. При этом необходимо постоянно контролировать расход каждой фракции для динамического изменения режима работы насоса скважины.
Например, если своевременно не обнаружить, что большую долю объема добываемой продукции составляет газ, то может произойти «завоздушивание» насоса, что приведет к его холостой работе и остановке скважины.
При существенном увеличении доли воды в добываемой смеси необходимо снизить частоту оборотов насоса или выключить его на некоторое время. В этом случае следует дать нефтяному пласту время на выделение нефти из слоя почвы и продолжить добычу спустя некоторое время.
Данные параметры непрерывно контролируются на устье скважины с помощью многофазного расходомера, состоящего из набора первичных преобразователей и вычислительного блока.
К первичным данным относятся следующие параметры: доплеровская скорость потока (вектор значений), Гц; газосодержание потока (вектор значений), %; скорость звука в смеси (вектор значений), м/с; давление смеси, Мпа; температура, °C.
Расчетные параметры следующие: расход жидкости, м3/сутки; расход газа, м3/сутки; обводненность продукции, %.
Представленный набор данных характеризует режим течения потока, что является важнейшим параметром при работе нефтяной скважины.
Существуют четыре основных класса режимов течения двухфазного потока в вертикальных каналах [9]: пузырьковый, снарядный, эмульсионный и дисперсно-кольцевой [10] (см. http://www.swsys.ru/uploaded/image/2020-3/ 2020-3-dop/15.jpg).
В данном случае необходимо решить задачу классификации контролируемых параметров нефтяной скважины по режимам течения нефте-водо-газового потока.
Теоретические расчеты, а также результаты многолетних испытаний нефте-водо-газового расходомера на сертифицированных эталонных стендах (в том числе и зарубежных) показали, что рассматриваемые контролируемые параметры монотонно характеризуют режим течения потока (см. http://www.swsys.ru/uploaded/image/2020-3/2020-3-dop/16.jpg, http:// www.swsys.ru/uploaded/image/2020-3/2020-3-dop/17.jpg).
Также установлена монотонная зависимость между первичными и расчетными данными, которая легла в основу построения вычислительной модели работы многофазного расходомера (см. http://www.swsys.ru/uploaded/ image/2020-3/2020-3-dop/18.jpg, http://www. swsys.ru/uploaded/image/2020-3/2020-3-dop/19. jpg).
Таким образом, показано, что рассматриваемая задача удовлетворяет ограничению функциональной разделимости для задачи классификации и, соответственно, к ней может применяться модифицированный метод опорных векторов.
Заключение
В статье рассмотрен метод SVM для решения задачи классификации, выделены его достоинства и недостатки. Разработан алгоритм FS-SVM (модификация алгоритма опорных векторов) для решения задачи классификации с ограничениями на предметную область.
Кроме того, сформулировано определение функциональной разделимости классов. Предложено использовать функциональную разделимость классов как ограничение, накладываемое на предметную область, которое позволит применить алгоритм FS-SVM.
Авторы вводят теорему (FS) для обоснования применимости алгоритма FS-SVM. Рассмотрено доказательство данной теоремы.
В качестве примера предметной области, в которой может применяться алгоритм FS-SVM, приводится задача классификации режимов течения нефте-водо-газового потока по исходных данным, регистрируемым многофазным расходомером на устье нефтяной скважины.
Работа выполнена при финансовой поддержке РФФИ, проект № 18-01-00459.
Литература
1. Башмаков А.И., Башмаков И.А. Интеллектуальные информационные технологии. M.: Изд-во МГТУ им. Н.Э. Баумана, 2005. 304 с.
2. Вьюгин В.В. Математические основы теории машинного обучения и прогнозирования. М., 2013. 390 с.
3. Statnikov A., Aliferis C.F., Hardin D.P., Guyon I. A Gentle Introduction to Support Vector Machines in Biomedicine: Vol. 1: Theory and Methods. 2011, 200 p. DOI: 10.1142/7922.
4. Rojo-Álvarez J.L., Martinez-Ramon M., Muñoz-Marí J., Camps-Valls G. Support vector machine and kernel classification algorithms. In: Digital Signal Processing with Kernel Methods. 2018, pp. 433–502. DOI: 10.1002/9781118705810.ch10.
5. Pisner D.A., Schnyer D.M. Machine Learning. Methods and Applications to Brain Disorders. 2020, pp. 101–121. DOI: 10.1016/B978-0-12-815739-8.00006-7.
6. Nefedov A. Support Vector Machines: A Simple Tutorial. 2016, 35 p. URL: https://svmtutorial.online (дата обращения: 20.01.2020).
7. Alam S., Kang M., Pyun J.Y., Kwon G.R. Performance of classification based on PCA, linear SVM, and Multi-kernel SVM. Proc. 8th ICUFN, IEEE 2016, pp. 987–989. DOI: 10.1109/ICUFN.2016.7536945.
8. Xiangdong H., Shaoqing W. Prediction of bottom-hole flow pressure in coalbed gas wells based on GA optimization SVM. Proc. 3rd IAEAC, IEEE, 2018, pp. 138–141. DOI: 10.1109/IAEAC.2018.8577488.
9. Баттерворс Д., Хьюитт Г. Теплопередача в двухфазном потоке; [пер. с англ.]. М.: Энергия, 1980. 328 с.
10. Киселев П.Т. Гидравлика: основы механики жидкости. М.: Энергия, 1980. 360 с.
References
- Bashmakov A.I., Bashmakov I.A. Intellectual Information Technologies. Moscow, 2005, 304 p. (in Russ.).
- Vyugin V.V. Mathematical Foundations of the Theory of Machine Learning and Forecasting. Moscow, 2013, 390 p. (in Russ.).
- Statnikov A., Aliferis C.F., Hardin D.P., Guyon I. A Gentle Introduction to Support Vector Machines in Biomedicine. Vol. 1: Theory and Methods. 2011, 200 p. DOI: 10.1142/7922.
- Rojo-Álvarez J.L., Martinez-Ramon M., Muñoz-Marí J., Camps-Valls G. Support vector machine and kernel classification algorithms. In: Digital Signal Processing with Kernel Methods. 2018, pp. 433–502. DOI: 10.1002/9781118705810.ch10.
- Pisner D.A., Schnyer D.M. Machine Learning. Methods and Applications to Brain Disorders. 2020,
pp. 101–121. DOI: 10.1016/B978-0-12-815739-8.00006-7.
- Nefedov A. Support Vector Machines: A Simple Tutorial. 2016, 35 p. Available at: https://svmtutorial.online (accessed January 20, 2020).
- Alam S., Kang M., Pyun J.Y., Kwon G.R. Performance of classification based on PCA, linear SVM, and Multi-kernel SVM. Proc. 8th ICUFN, IEEE, 2016, pp. 987–989. DOI: 10.1109/ICUFN.2016.7536945.
- Xiangdong H., Shaoqing W. Prediction of bottom-hole flow pressure in coalbed gas wells based on GA optimization SVM. Proc. 3rd IAEAC, IEEE, 2018, pp. 138–141. DOI: 10.1109/IAEAC.2018.8577488.
- Butterworth D. and Hewitt G.F. (Eds.). Two-Phase Flow and Transfer. Oxford Univ. Press, 1977 (Russ. ed.: Moscow, 1980, 328 p.).
- Kiselev P.T. Hydraulics: Fundamentals of Fluid Mechanics. Moscow, 1980, 360 p.

 (2)
(2)
 (3)
(3)

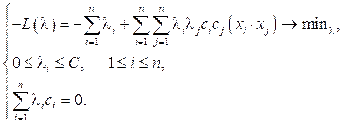
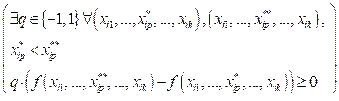 ,
,