Необходимость совершенствования математического аппарата теории классификации уже рассматривалась ранее [1]. Авторами предложен современный подход, основанный на применении фундаментальных алгебраических конструкций теории категорий [2]. Адекватность выбора данной теории обусловлена ее фрагментарным использованием в ряде работ, посвященных решению задачи классифика- ции [3]. При этом введен ряд определений, таких как однозначно не идентифицируемый объект A, категория однозначно не идентифицируемых объектов 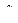, ковариантный функтор однозначно не идентифицируемых объектов F, дуальная категория однозначно не идентифицируемых объектов . В основу разрабатываемых теоретических положений включена система аксиом Бернайса–Геделя.

В известной литературе предложен ряд классических схем отнесения исследуемых объектов к тому или иному классу [3]. Пусть на категории однозначно не идентифицируемых объектов 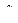 определены некоторое множество Xn, , и множество их классов толерантности 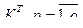. При этом  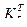⊂ Fu,  – множество промежуточных состояний; f = {f1, f2, f3, …, fg–1} – отношения эквивалентности (морфизмы) Fu. Их особенностью является непосредственное (прямое) установление отношения эквивалентности между объектом Xn, , и классом Kp, , где Kp Í F. Однако в настоящее время существует ряд актуальных прикладных задач в области классификации, требующих иного подхода к установлению отношения эквивалентности, а именно: вместо прямого отношения предлагается использовать модель каскадного фильтра с промежуточными состояниями, представленную на рисунке.

При установлении f1 определяется соответствие исследуемого элемента некоторому классу толерантности 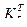. При этом может четко идентифицировать объект, тогда  = есть класс эквивалентности (класс A на рисунке). В противном случае  есть пе- ресечение классов идентифицируемых объектов (классы B, C, D на рисунке).

После наделения исследуемых классов структурой идентифицируемые объекты образуют пересечения в масштабах классов . Объем пересечений  представляет собой не что иное, как информационную неопределенность об объекте. Это дает основание задать на ней меру – меру информационной неопределенности (энтропии).

В данном случае энтропия интерпретируется как недостаток сведений о состоянии исследуемого объекта. Информация в той или иной мере устраняет эту неопределенность. Однако сведения, несущие информацию, могут содержать некую неопределенность, причем неопределенность двух типов: неточность сведения о состоянии объекта и определенную степень истинности данного сведения, то есть сведение может быть неабсолютно точным и неабсолютно истинным. Таким образом, в широком смысле неопределенность – векторный показатель, характеризующий неточность H и неистинность P сведений.

В части, касающейся рассмотрения аспекта неточности сведений, в нормативных докумен- тах допустимые значения неопределенностей результатов переработки информации задаются предельными погрешностями в единицах измерения соответствующих физических величин. Следовательно, применение мер неопределенности необходимо рассмотреть с точки зрения представления результатов в соответствующих единицах измерения физических величин, а не в условных (бит, дит и т.д.). Для обоснования приемлемой меры неопределенности предлагается использовать теоретические положения математического аппарата теории ультраоператоров [4–6].

Пусть дано множество W, содержащее точку W0, W0 Î d Ì W. Если d содержит те и только те точки Wi, которые обладают некоторым свойством, то возможно отождествление подмножества d с данным свойством [4–6]. При этом истинное высказывание представляет собой точку W0 из множества W, обладающую свойством d и являющуюся элементарным сведением о точке W0, представимой в виде одноместного предиката d(W0).

Таким образом, любое подмножество есть компакт d(W0), такой что W0 Î d(W0), при этом d(W0) Ì W – элементарное сведение о точке W0.

Пусть даны сведение d(W0) Ì W и семейство Ĩ сведений о точке W0, являющееся фильтром над подмножеством d(W0). Семейство Ĩ подмножеств некоторого множества называется фильтром, если выполняются условия: f Ï Ĩ, B Ì A, B Î Ĩ Þ A Î Ĩ, A, B Î Ĩ Þ A Ç B Î Ĩ [7].

Математическое определение информации введено в работах [6, 8, 9]. Семейство Ĩ подмножеств множества W-сведений о точке W0, являющееся фильтром над подмножеством d(W0), есть элементарная информация о точке W0. Иными словами, элементарная информация – это семейство всех истинных следствий и умозаключений, полученных средствами математической логики из истинного высказывания – элементарного сведения d(W0).

Если множества W, d измеримы (по Лебегу), то введенная на них мера может служить ме- рой неопределенности Н сведения d(W0) о точке W0 [8]. Неопределенность сведения d(W0) измеримого множества есть мера (Лебега) данного множества: H(d(W0)) = mes(d(W0)).

Мерой mes (необязательно Лебега) на полукольце множеств называется неотрицательная функция, принимающая конечные значения и являющаяся аддитивной [7, 8]:

A Ç B = f Þ mes(A È B) = mes(A) + mes(B), mes(f) = 0.

Исходя из определения меры введенная мера неопределенности неотрицательна и конечна, то есть ограничена, и удовлетворяет общим требованиям [8] к мерам неопределенности (неотрицательности, равенства нулю при отсутствии неопределенности, аддитивности):

1. H(d(W0)) ≥ 0;

2. d(W0) = W0 Þ H(d(W0)) = 0, d(W0) ≠ W0 Þ Þ H(d(W0)) > 0;

3. d1(W0) Ç d2(W0) = W0 Þ H(d1(W0) È È d2(W0)) = H(d1(W0)) + H(d2(W0)).

Допустим, множество W есть множество действительных чисел R. Пусть некоторое действительное число r Î R¢, R¢ Ì R, где R¢ – множество возможных значений r, являющееся отрезком на числовой оси. Тогда элементарным сведением о значении числа r является некоторый отрезок DR, r Î DR, DR Ì R¢.

Неопределенность Нr сведения о значении r есть длина DR Ì R¢, r Î DR, то есть Hr = │DR│.

Очевидно, что max Нr = Нr(DR º R¢) единиц измерения, min Нr = Нr(DR º r) = 0.

Значения неопределенностей Нxj обусловливают значение неопределенности Нy, однако при некоторых, в частности, нелинейных преобразованиях y = F(X), неопределенность Нy является функцией не только значений неопределенностей Нx аргументов, но и расположения областей неопределенностей Нx на множестве возможных значений аргументов.

Поскольку априори неизвестно, каковы будут значения аргументов и, следовательно, где будут расположены области их неопределенностей, для однозначности определения меры неопределенности результата преобразования в различных задачах следует вводить дополнительные условия. Исходя из принципа гарантированного результата следует ввести требование экстремальности (max, min, sup, inf) значения неопределенности Нy на множестве возможных значений аргументов. В работе [8] предложены ряд определений и соответствующая мера неопределенности.

Определение 1. Для задач, пессимистическим вариантом в которых является наименьшая неопределенность, существенная неопределенность Нy сведения о числе y (результате преобразования F) – есть минимальная неопределенность Нy сведения о числе y по множеству значений аргументов:

j = 1, …, J.

Определение 2. Для задач, пессимистическим вариантом в которых является наибольшая неопределенность, существенная неопределенность Нy сведения о числе y (результате преобразования F) – есть максимальная неопределенность Нy сведения о числе y по множеству значений аргументов:

j = 1, …, J.

Предлагаемый аппарат относительно близок к известному аппарату ультраоператоров теории ультрасистем [6], также оперирующих со сведениями в терминах определений неэлементарных сведений (рассмотрены ниже).

Отличие предложенного аппарата заключается в следующем:

-     предлагается оперировать не сведениями, а их неопределенностями, не рассматриваемыми в аппарате ультраоператоров;

-     в некоторых задачах рассматриваются элементарные сведения, что является частным случаем в аппарате ультраоператоров и облегчает вычисления;

-     область применения сужается до чисел (то есть сведения-множества могут быть только числовой природы, компактами, в том числе многомерными);

-     оперирование числовыми множествами-сведениями в некоторых случаях исключает необходимость применения в явном виде решетки (и соответствующих шкал) понятий и позволяют оперировать в неявном виде с бесконечными решетками.

Рассмотрим аспект истинности сведений.

Информация, сведения которой характеризовались двумя значениями истинности p – либо истина (р = 1), либо ложь (р = 0), уже приводилась ранее. В случаях, когда истинность сведения о точке может иметь не только эти два значения, но и некоторые промежуточные (0 < р < 1), возникает неэлементарная информация.

В [9] решеткой достоверностей называется произвольная решетка Р, в которой максимальный элемент трактуется как истина, а минимальный как ложь. Сравнимые элементы р1, р2 решетки достоверностей записывают р1 < р2. Решетка достоверностей, состоящая только из двух элементов {рmin = 0, рmax = 1}, называется элементарной, остальные – неэлементарными. Если неэлементарная решетка достоверностей линейно упорядочена, она называется вероятностной, иначе – модальной.

Таким образом, семантика всякого сведения предполагает наличие четырех величин: опорного множества W состояний объекта, семантического указателя W0 одного из состояний объекта W0 Î W, подмножества d состояний объектов из W, d Ì W, и семантической истинности р, которая характеризует истинность выполнения условия W0 Î d. При этом неэлементарное сведение обозначается кортежем <р, d(W0)>.

В исследованиях иногда полезно применение сведения, неопределенность которого равна максимально возможной, а вероятность, соответственно, единице.

В решаемой задаче введен ряд ограничений, в том числе ограничение на исследуемое исходное множество Xn, , являющееся конечным: M = card(Xn) < ¥. Поскольку имеющаяся неопределенность удовлетворяет всем свойствам, предъявляемым к информационной энтропии (доказательство не приводится из-за объема), и учитывается введенное ограничение, в качестве меры информационной неопределенности в классах с нечеткой структурой предлагается использовать меру неопределенности, предложенную в [8].

Результатом фильтрации на участках f2, f3, …, fg–1, а также функционирования предложенной модели в целом является  → 0, то есть максимальное снижение информационной энтропии и выделение четких объектов (классов) за счет введения ограничений фильтрации на каждом этапе в зависимости от условий решаемой задачи.

На основании изложенного можно сделать следующий вывод. Предлагаемый подход и представленные математическая модель и мера информационной неопределенности являются составной частью разрабатываемого метода классификации и кластеризации состояний сложных систем на основе теоретико-множественного подхода и позволяют рассматривать процесс получения четких классов с точки зрения снижения информационной энтропии с использованием каскадного фильтра. Дальнейшее развитие метода предполагает определение ограничений фильтрации, а также синтез алгебраических конструкций для решения задачи кластеризации.

Публикация выполнена в рамках государственного задания ФГУ ФНЦ НИИСИ РАН (фундаментальные научные исследования 47 ГП) по теме № 0065-2019-0001 «Математическое обеспечение и инструментальные средства для моделирования, проектирования и разработки элементов сложных технических систем, программных комплексов и телекоммуникационных сетей в различных проблемно-ориентированных областях» (АААА-А19-119011790077-1).

Литература

1.    Русаков К.Д., Селиверстов Д.Е., Смирнов А.Д. Разработка теоретических основ классификации и кластеризации нечетких признаков на основе теории категорий // XI Междунар. конф.: Управление развитием крупномасштабных систем. 2018. Т. 1. С. 320–322.

2.    Курош А.Г., Лившиц А.Х., Шульгейфер Е.Г. Основы теории категорий // УМН. 1960. Т. 15. № 6. С. 3–52. DOI: 10.1070/RM1960v015n06ABEH001116.

3.    Омельченко В.В. Общая теория классификации. Ч. 2: Теоретико-множественные основания. М.: Кн. мир, 2010. 295 с.

4.    Стинрод Н., Эйленберг С. Основания алгебраической топологии; [пер. с англ.]. М.: Физматгиз, 1958. 403 с.

5.    Eilenberg S., MacLane S. Relations between homology and homotopy groups of spaces. Ann. Math., 1945, vol. 46, pp. 480–509.

6.    Хиль С.Ш., Решетников В.Н., Савилкин С.Б. Применение нечеткой меры достоверности для анализа технического состояния летательных аппаратов в условиях нестохастической неопределенности // Программные продукты, системы и алгоритмы. 2019. № 3. С. 8–13. DOI: 10.15827/2311-6749.19.3.2.

7.    Генов А.А., Русаков К.Д., Хиль С.Ш. Идентификация состояния сложной технической системы в условиях неопределенности измерительной информации // Программные продукты и системы. 2017. Т. 30. № 3. С. 373–377. DOI: 10.15827/0236-235x.119.373-377.

8.    Князев В.В. Особенности обеспечения достоверности перерабатываемой логической информации в АСУ специального назначения // Вопросы защиты информации. 2009. № 2. С. 22–29. URL: http://izdat.ntckompas.ru/editions/for_readers/archive/article_detail.php?SECTION_ID=155;&ELEMENT_ID=12634 (дата обращения: 20.09.2020).

9.    Соболева Т.С., Чечкин А.В. Дискретная математика. М.: Академия, 2006. 256 с.

References

1. Rusakov K.D., Seliverstov D.E., Smirnov A.D. Development of the theoretical foundations for fuzzy feature classification and clustering based on the theory of categories. Proc. Intern. Conf. MLSD, 2018, vol. 1, pp. 320–322 (in Russ.).
2. Kurosh A.G., Livshits A.Kh., Shulgeifer E.G. Foundations of the theory of categories. Russian Math. Surveys, 1960, vol. 15, no. 6, pp. 3–52 (in Russ.). DOI: 10.1070/RM1960v015n06ABEH001116.
3. Omelchenko V.V. General Classification Theory. P. 2: Set-Theoretical Foundations. Moscow, 2010, 295 p. (in Russ.).
4. Steenrod N., Eilenberg S. Foundations of Algebraic Topology. Princeton, 1952, 323 p. (Rus. ed.: Moscow, 1958, 403 p.).
5. Eilenberg S., MacLane S. Relations between homology and homotopy groups of spaces. Ann. Math., 1945, vol. 46, pp. 480–509.
6. Hill S.Sh., Reshetnikov V.N., Savilkin S.B. Fuzzy measure of reliability to analyze aircraft technical condition in the context of non-stochastic uncertainty. Software Journal: Theory and Applications, 2019,
   no. 3, pp. 8–13 (in Russ.). DOI: 10.15827/2311-6749.19.3.2.
7. Genov A.A., Rusakov K.D., Hill S.Sh. Identification of a complex technical system functional state under conditions of measurement data ambiguity. Software & Systems, 2017, vol. 30, no. 3. pp. 373–377 (in Russ.). DOI: 10.15827/0236-235x.119.373-377.
8. Knyazev V.V. The features of ensuring the reliability of processed logical information in a special purpose ACS. Information Security Issues, 2009, no. 2, pp. 22–29. Available at: http://izdat.ntckompas.ru/
   editions/for_readers/archive/article_detail.php?SECTION_ID=155;&ELEMENT_ID=12634 (accessed Sep­tember 20, 2020).
9. Soboleva T.S., Chechkin A.V. Discrete Math. Moscow, 2006, 256 p. (in Russ.).