Моделирование освещенности и расчет глобального освещения широко применяются в настоящее время в архитектуре, дизайне новых устройств и новых материалов. Предварительные расчеты освещения и построение реалистичного изображения виртуальной модели повышают эффективность проектирования зданий. С их помощью можно заранее определить и добиться наилучшего воплощения целого ряда факторов, например, эстетичности разрабатываемых архитектором интерьеров помещений и внешнего вида. Важным аспектом строительства любого здания является экономичность (энергосбережение) его системы освещения. На основе точных расчетов освещения помещений дневным светом архитектор получает возможность спроектировать его максимальное использование, варьируя положение и ориентацию здания относительно сторон горизонта и окружающих строений, расположение и размеры оконных проемов. При проек- тировании офисных помещений освещенности рабочих мест должны соответствовать стандартам, в которых указаны минимально допустимые величины освещенности, доля прямого света от источника в поле видимости человека и другие параметры. Использование предварительных расчетов в процессе проектирования возможно только при применении достаточно точных вычислительных методов.
Наиболее последовательным и физически точным методом, позволяющим учесть многие аспекты распространения света в различных средах и его взаимодействие с объектами, является стохастическая трассировка лучей [1]. Трассировка лучей методом Монте-Карло (MCRT – Monte Carlo Ray Tracing) генерирует или преобразует лучи случайным образом с распределением вероятностей, определенным локально, то есть, например, в точке попадания луча в случае его рассеяния на поверхности или частицах, заданного с помощью двунаправленной функции распределения рассеяния (ДФР). Этот подход не является в конечном итоге оптимальным, например, ДФР может отправлять лучи в сторону от виртуального наблюдателя или камеры. Более того, в случае параллельного источника света возникает неоднозначность с точкой испускания луча: формально для параллельного света точка испускания луча должна выбираться равномерно в бесконечной области, что технически невозможно. Поэтому на практике точка испускания луча выбирается на проекции сцены на плоскость, ортогональную направлению луча, а излучение света определяется не только свойствами источника света, но и геометрией виртуальной сцены.
Если рассматривать построение реалистичного изображения внутренних интерьеров (например, офиса, построенное разработанной системой (см. http://www.swsys.ru/uploaded/ image/2020-4/2020-4-dop/2.jpg), то естественным продолжением такого подхода является дневное освещение через окна или открытые двери. В этом случае лучи, падающие на непрозрачные внешние стены, не усиливают внутреннее освещение, которое создается только лучами, проходящими через окна. Следовательно, необходимо выбирать источник луча в проекции окон на плоскость, перпендикулярную направлению освещения. Это основная идея оптимизации излучения света для интерьерных сцен. Однако должны быть правильно промоделированы и более сложные случаи: во-первых, когда источник дневного освещения задается не параллельным источником света, а небесной полусферой с распределением яркости; во-вторых, в случае с несколькими окнами, которые в проекции могут перекрываться.
При задании виртуальной сцены пользователю предоставляется возможность указать окна, открытые двери и люки. Затем распределение происхождения лучей маскируется 1 внутри или 0 вне их проекции. Однако такой подход может привести к ошибке, например, если в сцене дом окружен снегом, то есть сильно отражающей поверхностью. Солнечные лучи, отраженные снегом, значительно влияют на освещение интерьера, но они будут находиться вне проекции, так как свет излучается только к прозрачным окнам.
Эту ситуацию можно исправить, если сделать маску излучения более сложной, разрешив задавать ненулевые значения для некоторых непрозрачных областей, и, наоборот, давать значения меньше 1 для некоторых прозрачных областей, если они не открываются вовнутрь. В результате получаем некоторую функцию плотности вероятности источника излучения (PDF – Probability density function). Эта функция не может быть просто постулирована, а должна быть рассчитана на основе результатов моделирования. В этом случае данный метод принадлежит к широкому классу алгоритмов нахождения и использования оптимальной PDF в стохастической трассировке лучей.
Величины, представляющие интерес для оптического моделирования (например, яркость точки пересечения), как правило, являются интегралами произведения, например, точечная яркость – это свертка ДФР с освещением точки. Поэтому оптимальным распределением вероятности направления рассеянного луча в MCRT должно быть это произведение. Проблема в том, что один множитель этого произведения (в приведенном примере – освещение) сам является результатом стохастической трассировки и не известен заранее. Уже давно предпринимаются попытки повысить эффективность Монте-Карло трассировки лучей, делая PDF рассеянных лучей как можно ближе к этому произведению, используя различные приближения и эвристические методы. Скажем, яркость поверхности даже при прямом освещении распределеным источником света является интегралом по этой освещенной поверхности. Для повышения эффективности его расчета авторы работы [2] предложили выделить наиболее быстро меняющиеся члены подынтегрального выражения и использовать их для построения PDF. Исследования [3, 4] посвящены повышению эффективности обратной MCRT за счет рассеяния луча камеры не только по ДФР, но и по ее произведению с освещен- ностью точки. В [3] фотонные карты использовались для оценки углового распределения освещенности. В [4] это было сделано с 5D-деревом, покрывающим сцену, которая накапливала освещение, приносимое различными отраженными обратными лучами. Таким образом, удалось избежать отдельной фазы прямой трассировки.
С разработанным методом связаны две основные проблемы. Во-первых, оптимальное распределение теперь должно быть сохранено не в каждой точке попадания, а в каждом вокселе, что требует много памяти. Для его уменьшения используются различные приближения, например, довольно грубое пространственное разрешение. И это приводит ко второй проблеме: только довольно грубая оценка распределения входящего излучения. Таким образом, он отклоняется от целевого произведения, и разница должна быть компенсирована масштабом энергии луча. Наконец, можно оказаться в тупике с помощью методов, подобных [4], где освещение берется из тех же лучей трассировки, которые были испущены с помощью накопленной PDF. Например, если через какое-то время в каком-либо угловом конусе не было испущено ни одного луча, предварительно оцененное освещение от него равно 0. А при генерации следующего луча процедура отбора также не отправит луч в эту область, поэтому освещение от него остается равным 0 и далее. Самое простое средство борьбы с такой ошибкой – использовать смешанную стратегию, когда ДФР рассеивает некоторую долю лучей без использования накопленной PDF. Сложность заключается в том, как найти соотношение между лучами, которые необходимо генерировать с учетом PDF, и лучами без этого учета. Если оно слишком мало, то узкие пики освещения не повлияют на PDF и берутся только из небольшой доли лучей, рассеянных ДФР, которые создают сильный шум. Если отношение велико, это убивает само преимущество (ускорение) метода.
Эта основная идея была использована многими исследователями [5–9]. Если в [6] используется полусферическая PDF в форме, довольно похожей на работу Дженсена [3], то в [7] авторы используют приближение по сумме гауссианов. Его преимущество в том, что произведение двух гауссовских колоколов также является гауссовым и может эффективно отбираться. В [9] вместо этого используются вейвлеты. Некоторые авторы используют сферические гармоники, произведение которых также допускает аналитическую обработку. Используются и другие подходы, вплоть до нейронных сетей и машинного обучения, которые являются еще одним способом оптимизации PDF направления луча на основе накопленной статистики [8].
Все вышеперечисленные методы меняют PDF в одной точке, чтобы уменьшить дисперсию. Радикальным решением является метод Metropolis Light Transport [10], где, в отличие от MCRT, которая отслеживает луч сегмент за сегментом, случайным образом выбирается весь путь от источника света до камеры. Хотя проблема трассировки лучей устранена, появ- ляются другие проблемы, анализ которых вы- ходит за рамки данной статьи.
Менее радикальное решение по-прежнему использует MCRT, но применяет разные подходы (как для генерации направления рассеяния, так и для сбора освещенности) и генерирует сразу несколько траекторий лучей. Затем яркость пикселя берется как взвешенная сумма яркости, которую принесла каждая из траекторий. Обычно это называется стратегией множественной важности (multiple importance strategy). Этот метод не оптимизирует PDF в точках попадания отдельно, но вместо этого он смешивает вклады нескольких различных целых путей лучей. Основные идеи были предложены в [11], где, помимо всего прочего, доказано, что относительно простая эвристическая оценка баланса близка к оптимальной, то есть другие оценки рассматриваемого класса не могут существенно уменьшить дисперсию. Однако это не всегда так. В исследовании [12] авторы проанализировали условия в теореме Вича [11] и обнаружили, что иногда оценка может быть построена значительно лучше, чем эвристический баланс.
Освещение сцены через окна
Генерация лучей от источника света. Для параллельного источника света точки испускания луча распределены равномерно. С другой стороны, лучи, не попадающие в окно, бесполезны, так как не создают внутреннего освещения. Поэтому начало луча выбирается равномерно в проекции окна на плоскость, ортогональную направлению света.
В случае триангулированной геометрии сцены используются треугольники, которые составляют оконное стекло. Сначала выбираем один из них с вероятностью, пропорциональной потоку энергии через этот треугольник, а затем равномерно выбираем начало луча внутри треугольника. Возможно, что окно открыто или не имеет стекла внутри. В этом случае внутри окна нет треугольников для направления лучей. Тогда пользователь может выбрать треугольники, образующие раму окна. После этого из них строится выпуклая оболочка и лучи направляются на ее треугольники.
В случае непараллельного источника света расчет немного сложнее. Скажем, свет, образованный небесной полусферой, бесконечно далек, но у него в основном гладкое распределение яркости (гониограмма). Здесь сначала выбирается направление излучения v, а затем – треугольник t с вероятностью
 , (1)
, (1)
где St – площадь треугольника; t и nt – его нормаль. Начало луча x выбирается равномерно в этом треугольнике и переводится за пределы области сцены. Направление v выбирается с плотностью вероятности

 ,
,
где g – интенсивность гониограммы интенсивности.
Предположим, что небесная гониограмма задается таблицей на прямоугольной сетке (ϑ, j) и билинейно интерполируется внутри ячеек. Тогда сначала выбирается ячейка гониограммы [ϑi, ϑi+1]x[jj, jj+1] с вероятностью
 , (2)
, (2)
а затем в этой ячейке выбирается направление с плотностью вероятности
 . (3)
. (3)
Выбираем треугольник t с вероятностью (1). Если ячейка мала так, что направления излучения для всех ее четырех вершин находятся в одной и той же стороне от нормали треугольника, интеграл по ячейке равен
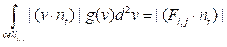 ,
,
где  зависит только от ячейки гониограммы, но не зависит от треугольника. Поэтому для ячейки гониограммы достаточно вычислить три значения –
зависит только от ячейки гониограммы, но не зависит от треугольника. Поэтому для ячейки гониограммы достаточно вычислить три значения –  и тогда для большинства треугольников поток через них вычисляется как скалярное произведение точек этого вектора с нормалью треугольника. Для тех немногих треугольников, которые освещаются с разных сторон ячейкой гониограммы, поток энергии необходимо рассчитать напрямую.
и тогда для большинства треугольников поток через них вычисляется как скалярное произведение точек этого вектора с нормалью треугольника. Для тех немногих треугольников, которые освещаются с разных сторон ячейкой гониограммы, поток энергии необходимо рассчитать напрямую.
Следовательно, в вышеупомянутом методе плотность вероятности начала и направления луча (x, v) равна

 (4)
(4)
где ct(x, v) = 1, если луч (x, v) пересекает треугольник t, и 0 в противном случае.
 Перекрытие проекции окон. Предложенный метод создает правильный поток энергии через поверхность, состоящую из треугольников (или других граней), проекции которых не перекрываются. Если проекции N треугольников пересекаются (рис. 1), числитель в (4) увеличивается для этой области, что вызывает искажение.
Перекрытие проекции окон. Предложенный метод создает правильный поток энергии через поверхность, состоящую из треугольников (или других граней), проекции которых не перекрываются. Если проекции N треугольников пересекаются (рис. 1), числитель в (4) увеличивается для этой области, что вызывает искажение.
Очевидное исправление состоит в том, чтобы изменить (4) на выражение
 , (5)
, (5)
где N(x, v) = ∑t Xt(x, v) – число треугольников, пересекающих луч (x, v).
С этим корректирующим фактором легко справиться с помощью метода отклонения: сначала выбираются направление и начало луча в соответствии с плотностью вероятности (4), то есть фактически с (1), (2) и (3), затем перебираются все треугольники всех окон и проверяется, пересекает ли их луч. Это делается для всех изолированных треугольников, то есть не имеет значения наличие других треугольников. Затем с вероятностью 1 – N–1(x, v) луч отклоняется, то есть заново выбираются направление луча и начало координат. Это продолжается до тех пор, пока луч не будет принят. Тогда результирующая плотность будет (4), и она обеспечивает правильное освещение.
Расчет оптимальной адаптивной функции PDF
Как видно из (5), вышеупомянутый подход маскирует собственную пространственно-од- нородную плотность вероятности источника света g(v) маской, которая равна 1, если луч пересекает любой оконный треугольник, и 0 в противном случае. Это простейшее изменение не является оптимальным. Рассмотрим более гибкий подход, когда происхождение и направление испускаемого луча выбираются с произвольной плотностью r(x, v).
После выбора луча источника света (x, v) его дальнейшее распространение определяется случайным образом в каждой точке пересечения. Соответственно, его вклад в яркость пикселя p является случайной функцией Lp(x, v). Естественно, если изменяется распределение лучей, это должно быть компенсировано изменением их вклада, чтобы сохранить математическое ожидание. Следовательно,

 ,
,
где Lp(x, v) – вклад для правильной плотности (5).
Предполагая, что траектория луча камеры является детерминированной, шум в p полностью обусловлен прямой Монте-Карло трассировкой лучей и может быть рассчитан как

 где
где  – усреднение по всем случайным путям луча, испускаемого источником света с началом x и направлением v. Общая ошибка – это просто сумма по всем пикселям. Вариация плотности вероятности при помощи dr изменяет эту суммарную ошибку на выражение
– усреднение по всем случайным путям луча, испускаемого источником света с началом x и направлением v. Общая ошибка – это просто сумма по всем пикселям. Вариация плотности вероятности при помощи dr изменяет эту суммарную ошибку на выражение
 (6)
(6)
Оптимальный r(x, v) минимизирует шум, и в этом экстремуме изменение должно уменьшаться до любого допустимого dr. Вариация нормализованной плотности, по определению, есть произвольная функция, для которой  Сравнивая с (6), делаем вывод, что она должна быть (общий вывод в методах Монте-Карло) следующей:
Сравнивая с (6), делаем вывод, что она должна быть (общий вывод в методах Монте-Карло) следующей:

или  , (7)
, (7)
где C – нормировочная константа.
 Значение
Значение  по определению, не зависит от того, как испускаются лучи (x, v). Перед трассировкой лучей создается четырехмер- ная сетка в пространстве (x, v). Затем, когда ис- пускается луч, находится ячейка, к которой принадлежит (x, v), и добавляется
по определению, не зависит от того, как испускаются лучи (x, v). Перед трассировкой лучей создается четырехмер- ная сетка в пространстве (x, v). Затем, когда ис- пускается луч, находится ячейка, к которой принадлежит (x, v), и добавляется  к значению, накопленному в этой ячейке. По мере трассировки лучей идет накопление все лучшей и лучшей оценки
к значению, накопленному в этой ячейке. По мере трассировки лучей идет накопление все лучшей и лучшей оценки  в каждой ячейке и начинается использование ее для оптимизации плотности. Начало и направление луча теперь выбираются с плотностью (7). По мере продолжения трассировки лучей и изменения накопленной оценки
в каждой ячейке и начинается использование ее для оптимизации плотности. Начало и направление луча теперь выбираются с плотностью (7). По мере продолжения трассировки лучей и изменения накопленной оценки изменяется и плотность излучения. Другими словами, теперь все зависит от времени. Это, однако, не создает петли обратной связи, потому что накопленное значение не зависит от выбора начала луча. Постепенно, когда накопленная оценка
изменяется и плотность излучения. Другими словами, теперь все зависит от времени. Это, однако, не создает петли обратной связи, потому что накопленное значение не зависит от выбора начала луча. Постепенно, когда накопленная оценка улучшается, плотность позиции начала луча сходится к своей предельной оптимальной форме.
улучшается, плотность позиции начала луча сходится к своей предельной оптимальной форме.
Результаты
Преимущество предложенных методов продемонстрируем на двух примерах.
Первая сцена задает внутреннюю комнату без окон, свет в которую может попасть только через щель под дверью. Дверь связывает ее с внешней комнатой, которая освещена дневным светом через дверь и большое окно (рис. 2). Камера находится во внутренней комнате и смотрит правее двери.
 На рисунке 3 представлены изображения для сцены «Внутренняя комната», рассчитанные в течение одного и того же времени. Средняя освещенность и среднеквадратичные значения по выделенному прямоугольнику, показанному на рисунке 3, приведены в таблице 1.
На рисунке 3 представлены изображения для сцены «Внутренняя комната», рассчитанные в течение одного и того же времени. Средняя освещенность и среднеквадратичные значения по выделенному прямоугольнику, показанному на рисунке 3, приведены в таблице 1.
Надо заметить, что выбор щели под дверью в качестве источника освещения, хотя и позволяет получить наименее зашумленную картинку, является неправильным. Эта щель находится в интерьере и не освещена снаружи по всей полусфере, как, например, окно в правой комнате, а вторичный свет от стен внешней комнаты также потерян, значит, мы явно занижаем освещенность. В результате средняя освещенность в выбранном прямоугольнике в 5,7 раза меньше, чем при правильном выборе окна. Также сама щель выглядит полностью черной, поскольку лучи попадают только в щель, а пол и вся внешняя комната не освещены. Для трех остальных вариантов можно видеть, что наименьший шум наблюдается во втором методе, при освещении через дверь и окно, выбранные пользователем. Средняя освещенность во всех трех вариантах одинаковая, в пределах точности вычислений.
Таблица 1
Значения освещенности (сцена «Внутренняя комната») (кд/м2)
Table 1
The average illumination (Scene “Inner room”) (cd/m2)
|
Освещение
|
Среднее
|
Среднеквадратичное
|
|
Без оптимизации
|
57,1
|
30,3
|
|
Через дверь и окно
|
57,7
|
11,7
|
|
Через щель
|
10,0
|
1,36
|
|
Адаптивное
|
57,1
|
18,2
|
Другой пример сцены показан на рисунке 4. Дом освещается дневным светом. Здесь много окон, через которые он может проникать внутрь. Поэтому второй метод (явное указание окон в сцене) неудобен.

 На рисунке 5 приведены изображения одной из комнат на втором этаже, рассчитанные в течение одного и того же временного интервала, без оптимизации излучения света (рис. 5а) и при использовании адаптивной функции PDF (рис. 5б). Значения средней освещенности и среднеквадратичной ошибки в области, обозначенной выделенным прямоугольником, приведены в таблице 2. Видно, что уровень шума заметно ниже (в 4,25 раза) при использовании адаптивной функции PDF. Визуально такое же качество изображения может было получено примерно в 18 раз быстрее при использовании функции PDF.
На рисунке 5 приведены изображения одной из комнат на втором этаже, рассчитанные в течение одного и того же временного интервала, без оптимизации излучения света (рис. 5а) и при использовании адаптивной функции PDF (рис. 5б). Значения средней освещенности и среднеквадратичной ошибки в области, обозначенной выделенным прямоугольником, приведены в таблице 2. Видно, что уровень шума заметно ниже (в 4,25 раза) при использовании адаптивной функции PDF. Визуально такое же качество изображения может было получено примерно в 18 раз быстрее при использовании функции PDF.
Таблица 2
Значения освещенности (внутренняя комната для сцены «Дом») (кд/м2)
Table 2
The average illumination (room for the scene "House") (cd/m2)
|
Освещение
|
Среднее
|
Среднеквадратичная ошибка
|
|
Без оптимизации
|
266
|
1 425
|
|
Адаптивное
|
203
|
335
|
Заключение
Разработанные авторами методы позволяют ускорить стохастическую трассировку лучей для интерьерных сцен, где интересующая область освещается снаружи через окна или  небольшие отверстия. Продемонстрирована математическая корректность предложенных методов. Оба метода снижают уровень шума или, что то же самое, позволяют быстрее достичь своего целевого уровня. Первый метод требует явной маркировки этих окон в геометрии сцены, что создает дополнительную нагрузку на пользователя, однако он дает лучшее шумоподавление. В случе неправильного выбора окна он может недооценивать освещенность, как это видно из первого примера, приведенного выше. Второй метод создает оптимальную функцию PDF излучения света, использование которой минимизирует шум. Это медленнее, но дает правильное освещение без необходимости явно маркировать окна и возможности допустить в этом ошибку. Тем не менее, второй метод ускоряет генерацию изображения в разы по сравнению с излучением света без оптимизации для всей области.
небольшие отверстия. Продемонстрирована математическая корректность предложенных методов. Оба метода снижают уровень шума или, что то же самое, позволяют быстрее достичь своего целевого уровня. Первый метод требует явной маркировки этих окон в геометрии сцены, что создает дополнительную нагрузку на пользователя, однако он дает лучшее шумоподавление. В случе неправильного выбора окна он может недооценивать освещенность, как это видно из первого примера, приведенного выше. Второй метод создает оптимальную функцию PDF излучения света, использование которой минимизирует шум. Это медленнее, но дает правильное освещение без необходимости явно маркировать окна и возможности допустить в этом ошибку. Тем не менее, второй метод ускоряет генерацию изображения в разы по сравнению с излучением света без оптимизации для всей области.
Оба метода были реализованы и встроены в комплекс моделирования освещенности и реалистичной визуализации Lumicept [13], разработанный в ИПМ им. М.В. Келдыша РАН. По умолчанию для интерьерных сцен всегда строится функция оптимального освещения PDF, которая позволяет значительно ускорить расчеты независимо от сложности виртуальной цены. Однако в простых случаях пользователю дается возможность маркировать окна, дыры или другие прозрачные поверхности. В таком случае расчеты еще ускоряются, но ответственность за правильность маркировки окон ложится на пользователя.
Литература
1. Pharr M., Humphreys G., Wenzel J. Physically Based Rendering, From Theory to Implementation. USA, SF, Morgan Kaufmann Publ., 2016, 1266 p.
2. Shirley P., Wang C., Zimmerman K. Monte Carlo techniques for direct lighting calculations. ACM TOG, 1996, vol. 15, no. 1, pp. 1–36. DOI: 10.1145/226150.226151.
3. Jensen H.W. Importance driven path tracing using the photon map. Proc. Rendering Techniques, 1995, pp. 326–335. DOI: 10.1007/978-3-7091-9430-0_31.
4. Lafortune E.P., Willems Y.D. A 5D tree to reduce the variance of Monte Carlo ray tracing. Proc. Rendering Techniques, 1995, pp. 11–20. DOI: 10.1007/978-3-7091-9430-0_2.
5. Burke D., Ghosh A., Heidrich W. Bidirectional importance sampling for direct illumination. EGSR, 2005, pp. 147–156. DOI: 10.2312/EGWR/EGSR05/147-156.
6. Hey H., Purgathofer W. Importance sampling with hemispherical particle footprints. Proc. 18th SCCG, 2002, pp. 107–114. DOI: 10.1145/584458.584476.
7. Herholz S., Elek O., Vorba J., Lensch H., Krivanek J. Product importance sampling for light transport path guiding. Comp. Graph. Forum, 2016, vol. 35, no. 4, pp. 67–77. DOI: 10.1111/cgf.12950.
8. Vorba J., Karlík O., Sik M., Ritschel T., Krivanek J. On-line learning of parametric mixture models for light transport simulation. ACM Trans. Graph., 2014, vol. 33, no. 4, art. 101, pp. 1–11. DOI: 10.1145/2601097. 2601203.
9. Clarberg P., Jarosz W., Akenine-Möller W., Jensen H.W. Wavelet importance sampling: efficiently evaluating products of complex functions. ACM Trans. Graph., 2005, vol. 24, no. 3, pp. 1166–1175. DOI: 10.1145/1073204.1073328.
10. Hachisuka T., Kaplanyan A.S., Dashsbacher C. Multiplexed metropolis light transport. ACM Trans. Graph., 2014, vol. 33, no. 4, art. 100, pp. 1–10. DOI: 10.1145/2601097.2601138.
11. Veach E., Guibas L.J. Optimally combining sampling techniques for Monte Carlo rendering. Proc. SIGGRAPH, 1995, pp. 419–428. DOI: 10.1145/218380.218498.
12. Sbert M., Havran V., Szirmay-Kalos L. Multiple importance sampling revisited: breaking the bounds. EURASIP J. Adv. Signal Processing, 2018, vol. 2018, art. 15. DOI: 10.1186/s13634-018-0531-2.
13. Жданов Д.Д., Потемин И.С., Галактионов В.А., Барладян Б.Х., Востряков К.А., Шапиро Л.З. Спектральная трассировка лучей в задачах построения фотореалистичных изображений // Программирование. 2011. № 5. C. 13–26.
References
- Pharr M., Humphreys G., Wenzel J. Physically Based Rendering, from Theory to Implementation. USA, SF, Morgan Kaufmann Publ., 2016, 1266 p.
- Shirley P., Wang C., Zimmerman K. Monte Carlo techniques for direct lighting calculations. ACM TOG, 1996, vol. 15, no. 1, pp. 1–36. DOI: 10.1145/226150.226151.
- Jensen H.W. Importance driven path tracing using the photon map. Proc. Rendering Techniques, 1995, pp. 326–335. DOI: 10.1007/978-3-7091-9430-0_31
- Lafortune E.P., Willems Y.D. A 5D Tree to reduce the variance of Monte Carlo ray tracing. Proc. Rendering Techniques, 1995, pp. 11–20. DOI: 10.1007/978-3-7091-9430-0_2.
- Burke D., Ghosh A., Heidrich W. Bidirectional importance sampling for direct illumination. EGSR, 2005, pp. 147–156. DOI: 10.2312/EGWR/EGSR05/147-156.
- Hey H., Purgathofer W. Importance sampling with hemispherical particle footprints. Proc. 18th SCCG, 2002, pp. 107–114. DOI: 10.1145/584458.584476.
- Herholz S., Elek O., Vorba J., Lensch H., Krivanek J. Product importance sampling for light transport path guiding. Comp. Graph. Forum, 2016, vol. 35, no. 4, pp. 67–77. DOI: 10.1111/cgf.12950.
- Vorba J., Karlík O., Sik M., Ritschel T., Krivanek J. On-line learning of parametric mixture models for light transport simulation. ACM Trans. Graph., 2014, vol. 33, no. 4, art. 101, pp. 1–11. DOI: 10.1145/2601097.
2601203.
- Clarberg P., Jarosz W., Akenine-Möller W., Jensen H.W. Wavelet importance sampling: efficiently evaluating products of complex functions. ACM Trans. Graph., 2005, vol. 24, no. 3, pp. 1166–1175. DOI: 10.1145/1073204.1073328.
- Hachisuka T., Kaplanyan A.S., Dashsbacher C. Multiplexed metropolis light transport. ACM Trans. Graph., 2014, vol. 33, no. 4, art. 100, pp. 1–10. DOI: 10.1145/2601097.2601138.
- Veach E., Guibas L.J. Optimally combining sampling techniques for Monte Carlo rendering. Proc. SIGGRAPH, 1995, pp. 419–428. DOI: 10.1145/218380.218498.
- Sbert M., Havran V., Szirmay-Kalos L. Multiple importance sampling revisited: breaking the bounds. EURASIP J. Adv. Signal Processing, 2018, vol. 2018, art. 15. DOI: 10.1186/s13634-018-0531-2.
- Zhdanov D.D., Potemin I.S., Galaktionov V.A., Barladyan B.Kh., Vostryakov K.A., Shapiro L.Z. Spectral ray tracing in problems of photorealistic imagery construction. Progr. and Comp. Soft., 2011, vol. 37,
no. 5, pp. 236–244. DOI: 10.1134/S0361768811050069.



 , (2)
, (2) . (3)
. (3)





