Термодинамические ограничения и информационные условия устойчивости, управляемости и робастности интеллектуального когнитивного управления
| Ульянов С.В. (ulyanovsv46_46@mail.ru) - Государственный университет «Дубна» – Институт системного анализа и управления, Объединенный институт ядерных исследований – лаборатория информационных технологий (профессор), Дубна, Россия, доктор физико-математических наук, Шевченко А.А. (allabard@yandex.ru) - Государственный университет «Дубна» – Институт системного анализа и управления (аспирант), Дубна, Россия, Шевченко А.В. (sh3vchenkoav@yandex.ru) - Государственный университет «Дубна» – Институт системного анализа и управления (аспирант), Дубна, Россия, Тятюшкина О.Ю. (tyatyushkina@mail.ru) - Государственный университет «Дубна» – Институт системного анализа и управления (доцент), Дубна, Россия, кандидат технических наук | |
| Ключевые слова: квантовый алгоритм самоорганизаций, неточные знания, термодинамика информационных процессов, когнитивные системы управления |
|
| Keywords: quantum self-organization algorithm, imperfect knowledge base, information process thermodynamics, , cognitive control system |
|
|
|
|
Стремительное развитие квантовой релятивистской механики и термодинамики заложило фундамент для нового поколения квантовых сквозных информационных технологий, что послужило основой развития квантовых инженерии (например, аппаратная реализация кван-тового компьютера), теории информации, программной инженерии, вычислений, криптографии, алгоритмов и программирования. Информационно-термодинамический закон распределения качеств управления, таких как устойчивость, управляемость и робастность, позволяет проектировать встраиваемые самоорганизующиеся интеллектуальные когнитивные системы управления, повышая эффективность технологических процессов и исполнительных устройств без изменения конструктивных решений (принцип неразрушения исполнительского уровня). Совместное включение в контур структуры системы управления когнитивного и интеллектуального (нечеткого) регуляторов позволяет использовать когнитивный потенциал человека-оператора и применять принцип компенсации ошибки управления от не- штатной ситуации управления соответствующей структурой регуляторов. При этом базы знаний (БЗ) регуляторов возможно спроектировать на основе квантового нечеткого вывода, реализующего квантовый алгоритм самоорганизации неточных БЗ. Более того, природа и сущность самого понятия «информация» могут рассматриваться как материальный физический объект, дающий возможность совершать полезную работу. Это позволяет установить механизм и возможности такой работы, не нарушая второго закона термодинамики, за счет корректных информационных моделей самого второго закона. В результате количество информации, извлеченное на квантовом уровне из когнитивных процессов, позволяет совершать на макроуровне количество полезной работы, большее по сравнению с работой, затраченной на ее извлечение на микроуровне, без нарушения второго закона термодинамики. При проектировании систем управления приходится учитывать не только известные в теории управления ограничения, но и новые физические явления и эффекты. Для практической реализации квантового подхода в процессе проектирования эффективных алгоритмов принятия решений и систем управления в условиях ограничений количества доступной информации требуется повышение уровня интеллектуальности, позволяющее включить в формируемые законы управления квантовые эффекты и явления. Термодинамическое распределение и соотношение критериев устойчивости, управляемости и робастности Для достижения необходимого уровня робастности и повышения интеллектуальности системы управления важно учитывать термодинамическое распределение, а также соотношение критериев устойчивости, управляемости и робастности интеллектуального управления. Рассмотрим динамический объект управления (ОУ), описываемый (в общем виде) уравнением
где q – вектор обобщенных координат, описывающий динамическое поведение ОУ; u – управляющая сила (выход исполнительного устройства системы автоматического управления (САУ)); t – время; S(t) – обобщенное производство энтропии системы «ОУ + регулятор». Необходимые и достаточные условия асимптотической устойчивости динамической системы, описываемой уравнением (1), определяются физическими ограничениями на вид функции Ляпунова, которая имеет два важных свойства: это строго положительная функция от обобщенных координат, то есть V > 0 (условие 1), полная производная по времени от функции Ляпунова является неположительной функцией, Согласно условиям 1 и 2 в качестве обобщенной функции Ляпунова выберем следующую функцию:
где S = Sp – Sc – производство энтропии в открытой системе «ОУ + регулятор»; Sp – производство энтропии в ОУ; Sc – производство энтропии в регуляторе (в исполнительном устройстве САУ). Отметим, что система (1) является открытой динамической системой в термодинамическом смысле, а основная задача регулято- ра – снижение энтропии динамического поведения ОУ. Поэтому стоит знак вычитания энтропии, производимой регулятором (а не плюс, как в случае замкнутой термодинамической системы), что приводит к понятию негэнтропии Бриллюэна. Введение энтропийных характеристик в (2) возможно в силу скалярного свойства энтропии как функции времени, S(t). Первое условие для функции Ляпунова (2) выполняется автоматически. Потребуем выполнения второго условия:
Таким образом, учитывая соотношение (1), имеем
Следовательно, взаимосвязь между устойчивостью по Ляпунову и робастностью, описанная уравнением (3), является основным физическим законом для проектирования САУ. Этот закон – основа для прикладной технологии проектирования БЗ робастных интеллектуальных систем управления (ИСУ) (с различными уровнями интеллектуальнос- ти [1, 2]) с использованием технологий мягких вычислений. Практическое применение физического закона процессов управления (3) к традиционным задачам, таким как оценка точности (грубости) линеаризации моделей ОУ, наблюдаемости параметров процессов управ- ления и др., рассмотрено в [1]. Следует отме- тить, что член Уравнение (3) связывает в аналитической форме такие качественные понятия теории управления u, как устойчивость, управляемость и робастность, на основе понятия энтропии феноменологической термодинамики с учетом совершения полезной работы регулятора. Данный подход позволяет, как отмечалось ранее, найти такое управление u, которое имеет необходимое распределение между уровнями устойчивости, управляемости и робастности и позволяет достигать цели управления в нештатных ситуациях с минимальным расходом полезного ресурса за счет применения в качестве функции пригодности в генетическом алгоритме минимума производства обобщенной энтропии, входящей в правую часть (3). Пример. Термодинамическая интерпретация информационной энтропии Шеннона – эквивалентность мер энтропий. Для оценки информационных возможностей интеллектуального когнитивного регулятора рассмотрим важную связь между термодинамической S и информационной H энтропиями. Рассмотрим для переменной X так называемую зета-функцию Хассе–Вейля (Hasse–Weil (HW)) следующего вида:
где Таким образом, в результате вычислений имеем прямое доказательство эквивалентности мер энтропий:
Рассмотрим теперь (3) с учетом приведенной связи термодинамической энтропии с информационной энтропией Шеннона. Определения термодинамической энтропии S и информационной H связаны соотношением фон Неймана [1] в виде S = kH = –k∑ipilnpi, где k ≈ 1,38∙10-23 Дж/К – постоянная Больцмана. Подставим в уравнение (3) вместо S(t) информационную энтропию Шеннона H. В результате получим
Таким образом, уравнение (4) на основе информационной энтропии Шеннона связывает устойчивость, управляемость и робастность, а также позволяет определять управление u для гарантированного достижения цели управления в нештатных ситуациях с требованием минимального количества информации о внешней среде и о состоянии объекта управления. Следовательно, уравнения (3) и (4) включают в себя перечисленные возможности применения физической или информационной энтропии проектируемого управления u в качестве полезного ресурса для достижения глобальной робастности ИСУ. Информационно-термодинамический закон квантовой самоорганизации интеллектуального управления Как отмечалось, уравнения (3) и (4) составляют систему уравнений, определяющую такое управление u, которое гарантирует достижение цели управления в нештатных ситуациях с минимальным расходом полезного ресурса и минимально требуемой исходной информацией. Рассмотрим некоторые особенности связи понятий количества информации и физической энтропии в свете приведенных уравнений (3) и (4). Так, определение физической энтропии дает возможность количественной формулировки второго закона термодинамики, который в изолированной системе запрещает процессы, сопровождающиеся уменьшением энтропии. Достаточно обратить внимание на формулировку связи функции Ляпунова и производства энтропии для замкнутой в термодинамическом смысле системы на рисунке 1 в виде Из определения функции Ляпунова динамическая устойчивость эволюции системы V > 0, При этом, однако, если возможен приток информации dI о системе, то есть если физическая система является изолированной только в тепловом, но не в информационном отношении, то указанный закон следует обобщить [5, 6], заменив неравенство dS ≥ 0 неравенством dS + dI ≥ 0. Поэтому, если имеется приток информации, можно тепловую энергию системы превратить в механическую без помощи холодильника. Таким образом, можно построить вечный двигатель второго рода, питающийся информацией. Особо следует подчеркнуть, что информационная форма обобщения второго закона термодинамики не отменяет его первоначальной формулировки. Отсюда следует заключение о необходимости энергетических затрат при измерении координат физической системы и записи этой информации. Если система находится при температуре T, то для получения и записи количества информации dI о ней необходимо потратить как минимум TdI энергии. В противном случае соединение автоматического измерителя и информационного преобразователя тепловой энергии в механическую дало бы вечный двигатель второго рода. Вывод о необходимости минимальных энергетических затрат распространяется также на физические каналы с шумом, соответствующим заданной температуре T. Таким образом, второй закон термодинамики накладывает некоторые ограничения на возможности физической реализации информационных систем, в частности, автоматов-измерителей и каналов передачи информации. Максимальное количество тепловой энергии, переходящее в работу, равно произведению абсолютной температуры на количество приходящей информации Больцмана. Приток информации о физической системе позволяет переводить тепловую энергию в работу без передачи части тепловой энергии холодильнику. Информация в этом смысле является также физическим процессом, способным создавать ресурс для совершения дополнительной полезной работы. Пример. Демон Максвелла. Возможность распространения описанного обобщения второго закона термодинамики на случай систем с притоком информации возникла давно в связи с обсуждением демона Максвелла. Последний, открывая и закрывая дверцу в стенке между двумя сосудами, в зависимости от скорости, с которой молекула подлетает к дверце, может создать разность температур или давлений, не совершая работы и нарушая второй закон термодинамики. В этом случае демону необходим приток информации. Пределы нарушения демоном второго закона термодинамики ограничены величиной приходящей информации. Это можно утверждать не только качественно, но и количественно согласно закону dS + dI ≥ 0, то есть в виде точного количественного закона. Обозначим через dQ количество теплоты, пришедшее из термостата. Запишем изменение энтропии термостата в виде Таким образом, если физическая система изолирована в тепловом отношении и о ней имеется количество информации I, то в системе возможны только такие процессы, для которых изменение суммарной энтропии превосходит (–I): ∆S ≥ –I. При этом нижняя граница физически достижима. Под тепловой изоляцией подразумевается то, что тепловая энергия, которую при указанных процессах можно превратить в работу, берется из самой системы, то есть термостат включен в данную систему. Второй закон термодинамики, как известно, нарушается для процессов, связанных с тепловыми флуктуациями, то есть является асимптотическим и не вполне точным. Можно дать уточненную формулировку: в теплоизолированной системе не могут происходить процессы, для которых приращение энтропии ∆S ≪ –1. Если брать энтропию в термодинамических единицах, то вместо 1 следует поставить постоянную Больцмана k. Тогда последнее соотношение примет вид ∆S ≪ –k. Соответственно, в уточненной формулировке запрещены процессы, для которых ∆S + I ≪ –1 или ∆Sфиз. + kI ≪ –k. Член с количеством информации I здесь существенен, если I ≫ 1 [7, 8]. Дальнейшие исследования позволили уточнить роль квантового второго закона термодинамики в квантовой теории информации, взаимосвязь понятий работы диссипативных процессов с понятиями относительного количества информации Фишера [9–12], а также связи понятия производимой рабо- ты с количеством приходящей информа- ции [13–16]. Таким образом, уравнения (3) и (4) включают в себя перечисленные возможности применения физической или информационной энтропии в качестве полезного ресурса для достижения глобальной робастности ИСУ. Пример. Работа диссипативных сил (как индикатор доступа к оценке затраченной системой работы). Определяется в терминах меры свободной энергии ∆F (отличие от равновесного состояния) как Wдисс.(Γ, λ) = = W(Γ, λ) – ∆F, где λ – параметр протокола; W(Γ, λ) означает усредненную работу, произведенную системой при воздействии внешних сил, и является функцией положения в фазовом пространстве Γ. Работа диссипативных сил представляет собой полное изменение производства энтропии системы как результат переноса потока тепла от действия внешних сил. Свободная энергия как мера различия конечных состояний системы называется также обратимой работой. Одновременно существует эквивалентное описание процессов с точки зрения статистического ансамбля реализации рассматриваемого процесса как последовательности бесконечно воспроизводимых траекторий данного процесса. Поэтому можно рассматривать работу диссипативных сил как усредненную величину 〈Wдисс.(Γ, λ)〉. При этом между величиной Wдисс.(Γ, λ) и информационным расхождением Кульбака–Лейблера существует следующая связь: Усредненный градиент работы диссипативных сил, производимой переходным процессом от состояния равновесия, эквивалентен расстоянию между прямым и обратным распределениями в фазовом пространстве, которое определяется количеством относительной информации Фишера. Пример. Квантовая система с диссипацией. В уравнениях движения квантовых систем диссипация описывается феноменологически логарифмической нелинейностью и феноменологической постоянной γ. В общем случае эволюция диссипативных процессов рассматриваемой динамической системы с гамильтонианом H описывается матрицей плотности ϱ в виде уравнения
где D(ϱ) – диссипативный оператор. В (5) предполагается в дальнейшем, что ͘ϱ(t) зависит только от настоящего времени t, то есть процесс без истории, t¢ < t. При γ = 0 имеем уравнение фон Неймана
решение которого сохраняет инвариант вида 〈S〉 = TrϱS и S = –lnϱ. Следует подчеркнуть, что решение уравнения (5) сохраняет инвариант как для чистых (ϱ2 = ϱ), так и для смешанных (ϱ2 ≠ ϱ) состояний. Для оператора 1) TrD(ϱ) = 0; 2) D(ϱ)† = D(ϱ); 3) D(ϱ1 ⊗ ϱ2) = D(ϱ1) ⊗ ϱ2 + ϱ1 ⊗ D(ϱ2). Если ввести обозначение D̃ и определить оператор D̃ как D(ϱ) = D̃(ϱ) ϱ, то получим D̃(ϱ1 ⊗ ϱ2) (ϱ1 ⊗ ϱ2) = = D̃(ϱ1)ϱ1 ⊗ ϱ2 + ϱ1 ⊗ D̃(ϱ2)ϱ2. (7) Выполняется следующее соотношение: 〈D̃(ϱ1 ⊗ ϱ2)〉 = 〈D̃(ϱ1)〉 + 〈D̃(ϱ2)〉, (8) то есть оператор D̃(ϱ) аддитивен. Решение функционального уравнения (7) имеет вид D̃1(ϱ) = –lnϱ = S, D̃2(ϱ) = 〈–lnϱ〉ϱ (9) или комбинацию из двух решений в (9). Для выполнения аксиомы TrD(ϱ) = 0 (сохранение вероятности) следует определить оператор D̃(ϱ) в виде D̃(ϱ) = S – 〈S〉‖ (10) или D̃(ϱ) = (〈S – 〈S〉‖〉)ϱ. (11) Оказалось, что формы (10) и (11) не являются единственными. В частности,
где А является эрмитовым оператором; [ ∙ , ∙ ] – антикоммутатор; A = A1 + A2 удовлетворяет соотношению (7). Из (5) следует обобщение (6) с учетом, например, (11) в виде
Таким образом, получено обобщение результатов на квантовые динамические системы и критерии физической реализуемости соответствующих математических моде- лей [17]. Следовательно, термодинамический критерий физической реализуемости выполняется – исследуемая математическая модель корректна. Информационные функции Ляпунова и квантовая функция Фишера В квантовой механике гильбертово пространство состояний связано с геометрией пространств, в которых введены меры различимости состояний и существует возможность определения чистых и смешанных состояний. Метрика данной различимости связана естественным образом с представлением длины траектории вычисления квантового алгоритма, и естественным вопросом явля- ется выявление отношения между данной длиной и вычислительной сложностью программы. В этом случае траектория в гильбертовом пространстве, определяемая квантовым алгоритмом, является геодезической в метрике Фубини–Штади (Fubiny–Study). Пример. Квантовые геометрические аналоги классических моделей кривизны в ин- формационной геометрии искривленных пространственно-временных континуумов. Рассмотрим в качестве примера факты геометрии пространства квантовых состояний. Расстояние между двумя квантовыми состояниями |ψ1〉 и |ψ2〉 можно определить различными способами. Например, широко применяемые меры расстояния FS и Wootters (W) определяются соответственно в следующем виде: и где γ – постоянная величина. Несмотря на внешнее различие, данные меры расстояния эквивалентно определяют расстояние между квантовыми состояниями. Так, для близких состояний, когда |〈ψ1|ψ2〉|2 = 1 – δ2, где δ – малая величина, имеем соотношение d(FS) = = d(W) = γδ. Подобным образом определяются другие меры расстояний. Аналогично данному результату элементы длины для семейства (множества) векторов квантовых состояний |ψ(ξ1, ξ2, …, ξk)〉 параметризованных k параметрами ξ1, ξ2, …, ξk, определенные на заданных метриках расстояния, эквивалентны для различных определений расстояния ds2 = gijdξidξj с метрическим тензором gij = γ2 Re(〈ψi|ψj〉 – 〈ψi|ψ〉〈ψ|ψj〉), где Приведенная форма метрики расстояния применяется на практике многими исследователями, и обычно принимается γ = 2. Тогда для двумерного случая gij является метрическим тензором сферы с единичным радиусом (сфера Блоха). При рассмотрении эволюции квантового состояния, описываемой уравнением Шредингера, вводится понятие скорости кван- товой эволюции |ψ(ξ)〉 = C [(1 – ξ)|ψ0〉 + ξ|ψ1〉 eiϕ], (14) где ξ – параметр, принимающий значения от 0 до 1. Фазовый множитель eiϕ выбирается следующим образом. Векторы |ψ0〉 и |ψ0〉 eiϕ0 определяют эквивалентные квантовые состояния. Поэтому требуется выполнение условия эквивалентности геодезических линий, определенных между состояниями |ψ0〉 и |ψ1〉 и состояниями |ψ0〉eiϕ0 и |ψ1〉eiϕ1. Данное условие выполняется, если выбрать Отметим, что геодезическая линия (14) является множеством состояний и существует много способов ее параметризации. В геометрии квантовых состояний показано, что длина кривой в квантовом пространстве состояний не зависит от пути ее параметризации [18, 19]. Для вычисления длины геодезической линии удобно представлять определяющее ее уравнение в виде
где новый параметр 0 ≤ θ ≤ π и константа нормализации Подчеркнем, что (14) и (15) адекватно описывают однопараметрическое семейство векторов квантовых состояний в виде геодезических линий. Используя определение метрики как gij = γ2 Re(〈ψi|ψj〉 – 〈ψi|ψ〉〈ψ|ψj〉) для однопараметрического множества состояний (15), получим S = ∫ds = γ arccos|〈ψ1|ψ0〉|. (16) Таким образом, выражение (16) для длины геодезической линии совпадает с выраже- нием метрики Wootters расстояния между векторами квантовых состояний. Аналогично можно вычислить длину кривой (14), соединяющей состояния |ψ0〉 и |ψ1〉, для определенной фазы ϕ. Тогда геодезическая линия определяется как кривая минимальной длины на семействе кривых. Минимальная длина достигается при установленном выше условии Кривизна. Вектор состояния квантовой эволюции от одного параметра, такого как время t, определим в виде однопараметрического множества векторов состояний |ψ(t)〉 = = exp{–iHt}|ψ0〉, генерируемого гамильтонианом системы. Отклонение вектора состояний |ψ(t)〉 от геодезической линии, связывающей состояния |ψ0〉 и |ψ1〉, определяется через кривизну пространства. Для введения понятия кривизны рассмотрим случай эволюции из двух состояний |ψ0〉 в |ψ1〉. На первом этапе предположим, что осуществляется эволюция в течение отрезка времени ∆t из начального состояния |ψ0〉 в промежуточное |ψ¢〉 в виде
где H – не зависящий от времени гамильтониан. Без потери общности в дальнейшем принимается ∆t = ∆t¢. Отклонение квантовой эволюции от геодезической линии, связывающей состояния |ψ0〉 и |ψ1〉, может быть охарактеризовано максимальным значением величины |〈ψ¢|ψ(ξ)〉|2 параметризованной ξ. При max|〈ψ¢|ψ(ξ)〉|2 = 1 состояние |ψ’〉 принадлежит геодезической линии. Отклонение |ψ¢〉 от геодезической увеличивается с уменьшением величины max|〈ψ¢|ψ(ξ)〉|2. Обычно вводится выражение 1 – max|〈ψ¢|ψ(ξ)〉|2 = min(1 – |〈ψ¢|ψ(ξ)〉|2), которое эквивалентно нулю, когда отклонение равно нулю, и положительно возрастает, когда отклонение увеличивается. Нетрудно заметить, что данное выражение эквивалентно метрике расстояния FS. Дополнительная точка зрения на квантовый алгоритм может быть рассмотрена с позиции траекторий в пространстве унитарных преобразований. При заданной траектории |ψ(s)〉 квантового алгоритма можно определить оператор U таким образом, что выполняется соотношение U|ψ(0)〉 = |ψ(1)〉, определить программу как траекторию в пространстве унитарных операторов O(s), и при этом выполняется O(s = 0) = 1 и O(s = 1) = U. В таком случае вычислительная сложность заданной программы определяется количеством гейтов, необходимых для определения реализации данной траектории квантового алгоритма. Рассматриваемая траектория генерируется однозначно унитарным оператором H, который идентифицируется как гамильтониан системы, формирующий структуру квантового алгоритма и его эволюцию вдоль траектории. Тогда можно записать O(t) = = e-iHtO(0)eiHt и аналогично для |ψ(t)〉. В случае выполнения условия [H, O(0)] ≠ 0 возникает вопрос о том, как потенциально простой начальный оператор O(0) принимает в процессе эволюции во времени сложную структуру. Для заданной траектории O(s) возможно ввести определение оператора Ляпунова Ls в виде решения уравнения Ляпунова:
Для найденного решения Ls можно определить функцию квантовой информации Фишера F(s) как Допустим, что рассматривается траектория оператора O(s), определено однопараметрическое семейство собственного базиса |ϕn(s)〉 в виде O(s)|ϕn(s)〉 = ρn(s)|ϕn(s)〉. В этом базисе имеем O(s) = ∑nρn(s)|ϕn(s)〉´ ´ 〈ϕn(s)|. Рассмотрим уравнение Ляпунова для оператора траектории O(s) и разрешим уравнение для определения Ls. Тогда имеем
где |∂sϕn(s)〉 = ∑mLm,n|ϕm(s)〉. Оператор Ляпунова Ls в случае, когда задан гамильтониан эволюции H, определяет траекторию O(s) = e-iHsO(0)eiHs. Применяя к O(0) представление в виде O(0) = ∑n ρn|ϕn〉〈ϕn|, как результат получаем Ls = eiHsL0e-iHs с учетом (см. [20]), что
С определением функции оператора Ляпунова Ls определяется квантовая функция Фишера Из изложенного следует, что при построении математической модели необходимо проверять ее корректность, устойчивость и условия термодинамического критерия физической реализуемости: нарушение хотя бы одного из этих условий ведет, по существу, к нарушению остальных условий. При этом необходимо, чтобы условия корректности и устойчивости исследуемой математической модели совпадали с соответствующим понятием их устойчивости. Этот вывод является обоснованием часто встречающейся в системной инженерии интуитивной замены понятия корректности обыкновенных дифференциальных уравнений на понятие их устойчивости. Следовательно, выбор физического базиса проведения эксперимента и определение ма- тематического способа (задания критерия корректного описания) модели ОУ существенно влияют на качество интерпретации результата процесса обработки экспериментальных данных и извлечения объективных знаний из динамического поведения само- го ОУ. Информационно-термодинамические условия и ограничения на возможность совершения полезной работы на основе извлеченной информации Современная физика (феноменологическая термодинамика) утверждает, что необходимо совершить полезную работу для извлечения количества информации о поведении исследуемой системы, затратив при этом дополнительный энергетический ресурс и вместе с этим потеряв полезную работу за счет возрастания энтропии в поведении исследуемого объекта и системы измерения извлекаемой информации – физический закон интеллектуальной ИТ образовательного процесса. В этом случае справедливы [21] следующие информационно-термодинамические ограничения:
где Пример. Информационно-термодинамические оценки затрат ресурса на извлечение количества знаний из процессов измерения. В микросистемах термодинамические величины, такие как работа, тепло и внутренняя энергия, не являются постоянными величинами и флуктуируют. Случайные флуктуации могут нарушать второй закон термодина-мики, но в среднем второй закон термодинамики на макроуровне выполняется, если начальное состояние системы находится в тепловом равновесии, то есть 〈∆F – W〉 ≤ 0, где, как и ранее, ∆F – свободная энергия как мера различия между состояниями системы; W – совершаемая работа; знак 〈 〉 означает усреднение по ансамблю множества состояний системы. Однако управление с обратной связью позволяет целенаправленно выборочно манипулировать только флуктуациями так, что выполняется строгое неравенство ∆F – W > 0. Данное выражение эквивалентно использованию информации о поведении системы [22] – прототип демона Максвелла. Термин «обратная связь» означает, что выбор стратегии управления зависит от результатов измерений на выходе системы управления. Другими словами, метод управления с обратной связью эквивалентен применению систем управления с замкнутым контуром. Управление с обратной связью позволяет использовать информацию в качестве ресурса в виде свободной энергии системы [23]. Отметим, что Сциллард разработал модель преобразования одного бита информации в свободную энергию (или работу) в количестве kBTln2. Таким образом, второй закон термодинамики обобщается в виде 〈∆F – W〉 ≤ kBTI. Здесь I означает количество взаимной информа- ции, извлеченной измерением состояния системы, то есть является объективной величиной [24, 25]. Следовательно, демон Максвелла (по типу Сцилларда) – это активный интеллектуальный агент, который способен оценить вход (используемое содержание информации) и выход (приобретенную энергию) при управлении с обратной связью, реализует идею преобразования информации в энергию и является информационно-термодинамическим решением обратной проблемы оценки потерь на извлечение информации о свойствах модели ОУ. Благодаря синергетическому эффекту создается дополнительный информационный ресурс и мультиагентная система способна решать сложные динамические задачи для выполнения командной работы. Данная задача не может быть выполнена каждым элементом (агентом) системы отдельно в различных средах без внешнего управления, контроля или координации, однако обмен знаниями и информацией позволяет выпол- нять полезную командную работу для достижения цели управления в условиях неопределенности исходной информации и ограничений на возможное потребление полезных ресурсов. В частности (см. пример ниже), для систем управления с обратной связью объем извлекаемой полезной работы удовлетворяет неравенству
где k – это постоянная Больцмана; Tmin(t) интерпретируется системой как самая низкая достижимая температура во времени t для контроля обратной связи, предполагая T(0)min; Ic определяет количество информации Шеннона (перенос энтропии), извлеченное системой из процесса измерения.
Ошибка управления содержит информацию о непредвиденной ситуации управления и поступает на входы рассматриваемых регуляторов. Выходные сигналы регуляторов отражают реакции БЗ, которые в общем случае являются неполными и могут приводить к потере робастности системы управления. Оба сигнала поступают в блок квантового нечеткого вывода, осуществляющий самоорганизацию неполных БЗ, формируя в реальном времени новую робастную БЗ гибридного квантового интеллектуального когнитивного регулятора. Обобщением уравнений (3) и (4) является следующая система уравнений:
где (STc + SCc) и (HTc + HCc) означают совместные термодинамические и информационные энтропии технического интеллектуального и когнитивного регуляторов соответственно. Обсудим особенности соотношения (18) применительно к системе уравнений для интеллектуального когнитивного управления (19) и (20). Известное выражение второго закона феноменологической термодинамики утверждает, что максимальное (усредненное) количество работы, извлекаемое из системы при взаимодействии с простым тепловым резервуаром, не может превышать количества свободной энергии и проявляет стремление к понижению при переходе системы из начального в конечное состояние. Однако, как следовало из анализа поведения теплового двигателя (тепловой машины) Сцилларда, возможно нарушение такого ограничения при допущении предположения о доступности дополнительной информации интеллектуальному агенту, извлекающему на ее основе работу из тепловой машины (открытая система с информационным обменом). Для учета такой возможности второй закон феноменологической термодинамики обобщается на основе введения наблюдателя (демона) с контуром управления обратной информационной связью. В частности, показано, что при применении управления с обратной информационной связью количество извлекаемой работы W должно удовлетворять неравенству типа (17) следующего вида: W ≤ kITc, (21) где k – постоянная Больцмана; T – темпера- тура теплового резервуара; Ic определяет так называемый перенос энтропии к регулятору от системы измерения [26, 27]. При этом предполагается, что при переходе от начального к конечному состоянию снижения свободной энергии не происходит. Имеется также возможность разработать протоколы обратных связей, позволяющие сформировать уравнения определения W, применяя обратимые и квазистатичные преобразования. В первом приближении данного подхода определяется составляющая конечного времени для определяющего W уравнения, характеризующая максимальную работу, которую можно извлечь с применением управления с обратной связью, в терминах переноса энтропии. Результат описывается на основе исследования поведения существенно демпфированной системы на основе модели решения уравнения Ланжевена. Максимальное количество извлекаемой работы за период t, Wmax(t), определяется [28] через интеграл вида
Здесь Tmin(t) интерпретируется как наименьшая температура, достигаемая системой за время t непрерывного управления с обратной связью при предположении, что начальное значение равновесия системы Tmin(0) = T. Так как Tmin(t) ≤ T, верхняя граница в (22) получается из применения (21). Количество переноса энтропии Ic(t) определяется через количество передаваемой информации регулятору от системы измерений в интервале [0, t]. Поэтому оптимально применяемое количество переноса энтропии регулятором позволяет извлечь полезную (от kTminln2 до kTln2) работу. Кроме того, для широкого класса динами- ческих систем получено выражение для определения количества переноса энтропии Ic(t), применимое для случая как непрерывного, так и дискретного времени. В частности, новое соотношение получено в замкнутой математической форме для определения количества переноса энтропии (вне зависимости от закона и применяемого вида обратной связи). Для линейных систем размерности, превышающей единицу, то есть для динамических систем с квадратичным гамильтонианом и контактом с тепловым резервуаром, показано выполнение соотношения
и выполняется равенство асимптотически t → ∞, то есть система находится в неравновесном состоянии. Более того, для всех состояний выполняются неравенство W ≤ kTIc(t) и второй закон для конечных интервалов времени. Квадратичная форма гамильтониана является типовой для систем с тепловыми флуктуациями при комнатной температуре, находящихся в состоянии с минимальной энергией. Теория оптимального управления дает возможность вычислить Tmin(t) и опре- делить характер закона обратной связи, например, для линейных систем по принципу разделения переменных, наблюдения параметров траекторий и управления. Оценка измерения траектории может быть дана эффективно на основе применения фильтра Калмана–Бьюси, который позволяет максимально эффективно использовать информацию, содержащуюся в измерениях на основе минимума вариаций оценки ошибки.
Демон имеет возможность наблюдать величину тока i и имеет доступ к измерению шума напряжения ϑmeas. Резистор содержит случайный шум, описываемый моделью Джонсона–Найквиста. Схема на рисунке 3 моделируется на основе существенно демпфированного уравнения Ланжевена следующего вида:
где ϑ(0) – гауссовский шум; w и wmeas – некоррелированные гауссовские белые шумы (〈w(t)w(t¢)〉) = 〈wmeas(t)wmeas(t¢))〉 = δ(t – t¢))); Vmeas – интенсивность измеримого шума; τ = RC – постоянная величина открытой системы. Шум измерения
Эффективная текущая температура (кинетическая температура) емкости обозначается как TC, а внутренняя энергия – U. Напряжение ϑmeas является измеримой величиной и «питает» демона информацией: физически означает измерение флуктуирующего шума напряжения в емкости ϑ демоном. Данная задача оптимизации решается в режиме (без информации о траекторной реализации
где K является функцией времени и подлежит определению. Для фиксированных уровней шума существует оптимальное значение коэффициента усиления В результате применение методологии динамического программирования приводит к исследованию уравнения фильтра Риккати, которое для рассматриваемой задачи записывается в следующем виде:
где оптимальный коэффициент усиления K выражен параметризацией через решение Для получения оценки максимальной работы в (23) необходимо иметь оценку информационного потока по непрерывному каналу обратной связи неопределенной части измеримого напряжения ϑ в виде измеримой величины ϑmeas. Такой величиной является перенос энтропии [28]. Оценка непрерывного по времени предела переноса энтропии имеет следующий вид:
Такая величина называется количеством взаимной информации между неопределенным начальным значением напряжения ϑ(0) и случайными значениями траектории теплового шума w, возникающего при измерении траектории ϑmeas. Количество взаимной информации двух случайных величин ξ и θ определяется в виде
и эквивалентно количеству (дифференциальной) энтропии Шеннона случайной величины ξ, убывающей при наличии знаний о случайной величине θ, и наоборот. Здесь Pθξ, Pθ и Pξ описывают взаимные и маргинальные меры распределения вероятностей случайных величин θ и ξ. Тогда для данной задачи количественно перенос энтропии определяется следующим выражением:
Отметим, что Ic не зависит от описания природы демона, например, деталей описания коэффициента его усиления обратной связи G. Сам демон может оптимально управлять извлечением работы (23) с помощью использования измерений ϑmeas и выбора инжекции тока i. На интуитивном уровне интерпретации демон может воспроизводить положительную работу со скоростью Модель демона традиционно рассматривают как слабо наблюдаемую систему с малыми флуктуациями, при действии на которую энергия извлекается в противоречии второму закону термодинамики. В более со-временной интерпретации демон рассматри- вается как регулятор, содержащий систему измерения (цифровой или аналоговый вычислитель), способный определить наиболее оптимальное действие для реализации исполнительным устройством. Извлеченная информация должна храниться в памяти компьютера в период необходимого использования. Демон Ландауэра–Пенроуза–Беннета рассматривает память компьютера совместно с принципом Ландауэра, согласно которому для стирания одного бита при температуре T необходимо затратить на преодоление диссипативных сил теплового резервуара работу как минимум kTln2 как ключевой позиции для восстановления выполнения условий второго закона термодинамики. Если наблюдателю в виде демона Максвелла доступны микроскопические степени свободы, то второй закон термодинамики может быть нарушен. Сциллард показал из анализа модели демона Максвелла, что из термодинамического цикла извлекается работа в виде kTln2. Более того, извлекаемая из системы работа
Заключение Отметим некоторые дополнительные выводы из анализа особенностей информационно-термодинамического закона квантовой самоорганизации когнитивных робастных ИСУ на рисунке 4 с позиции теории динамических робототехнических систем.
Приведенные на рисунке 4 соотношения характерны для диссипативных объектов управления с высокоэнергетическими уров-нями, а также для применяемых в данных объектах регуляторов с обратной связью без потерь с низким энергетическим уровнем. В этом общем случае энергия стремится к передаче управления от объекта регулятору, тем самым энергия объекта управления убывает, энергия регулятора увеличивается и энергия эмуляции (но не физическая энергия) аккумулируется регулятором. И наоборот, если применяемый регулятор с высоким энергетическим уровнем, то энергия может передаваться от регулятора объекту управления, так как регулятор может воспроизводить реально физическую энергию для управления достижимостью требуемого энергетического потока. Тогда, если состояния регулятора совпадают с высоким уровнем энергии эмуляции, возможно восстановить данные состояния, удаляя энергию эмуляции так, что энергия эмуляции не возвращается к объекту управления. В этом случае общая замкнутая система состоит из объекта управления и регулятора и обладает прерывистыми потоками, такими, что возможно организовать логическое переключение в сочетании с непрерывной динамикой и сформировать модель описания на основе импульсных дифференциальных уравнений [29]. Основная цель робастного интеллектуального когнитивного управления заключается в поддержке оптимального соотношения в распределении качеств управления, таких как устойчивость, управляемость и робастность, при выполнении термодинамических и информационных соотношений (рис. 4) и выполнении роли информационно-термодинамического компенсатора стабилизации процессов управления. Множество обнуления определяется как множество всех точек в пространстве состояний регуляторов с замкнутыми обратными связями, которому соответствуют регуляторы с убывающей энергией эмуляции. При обнулении состояний регулятора энергия объекта управления никогда не может возрастать после первого же события обнуления состояний. Более того, если энергия замкнутой системы управления сохраняется между со- бытиями обнуления состояний регулятора, убывание энергии объекта управления сопровождается соответствующим возрастанием энергии эмуляции. Таким образом, поддержка оптимального информационно-термодинамического распределения между устойчивостью, управляемостью и робастностью за счет процессов самоорганизации знаний может быть реализована при помощи нового квантового алгоритма управления самоорганизацией знаний в виде неточных БЗ на основе операций квантовых вычислений, которые отсутствуют в технологиях мягких вычислений. Приведенные соотношения между ко- личеством информации, извлекаемой свободной энергии и работы подтверждают от- меченный выше вывод: робастность ИСУ возможно повысить за счет производства энтропии когнитивного регулятора, который уменьшает потери полезного ресурса объекта управления, а негэнтропия когнитивного регулятора снижает требования к минимуму исходной информации для достижения робастности. Поэтому извлекаемая информация, основанная на знаниях в БЗ когнитивного регулятора, позволяет получить дополнительный ресурс для совершения полезной работы, что эквивалентно появлению целенаправленного действия на объект управления для гарантированного достижения цели управления. Литература 1. Петров Б.Н., Уланов Г.М., Гольденблат И.И., Ульянов С.В. Теория моделей в процессах управления: Термодинамические и информационные аспекты. М.: Наука, 1978. 224 с. 2. Ulyanov S.V. Self-Organized Intelligent Control System. US Patent no. 6,411,944B1.2002. 3. Marcolli M. Motivic information. Bollettino dell'Unione Matematica Italiana, 2019, no. 12, pp. 19–41. DOI: 10.1007/s40574-018-0167-z. 4. Combe C.N., Manin Yu.I., Marcolli M. Geometry of information: classical and quantum aspects. ArXiv, pp. 1–44. URL: http://www.its.caltech.edu/~matilde/GeometryInformationFmflds.pdf (дата обращения: 1.08.2021). 5. Стратонович Р. Теория информации. М.: Советское радио, 1975. 424 с. 6. Yufik Y. The understanding capacity and information dynamics in the human brain. Entropy, 2019, vol. 21, no. 3, pp. 308. DOI: 10.3390/e21030308. 7. Brandao F.G.S.L., Horodecki M., Ng N.H.Y., Oppenheim J., Wehner S. The second laws of quantum thermodynamics. PNAS, 2013, vol. 112, no. 11, pp. 3275–3279. DOI: 10.1073/pnas.1411728112. 8. Sagawa T. Thermodynamic and logical reversibilities revisited. J. of Statistical Mechanics: Theory and Experiment, 2014, vol. 2014, no. 3, pp. 3–25. DOI: 10.1088/1742-5468/2014/03/P03025. 9. Yamano T. Phase space gradient of dissipated work and information: A role of relative Fisher information. J. of Mathematical Physics, 2013, vol. 54, no. 11, art. 113301. DOI: 10.1063/1.4828855. 10. Ilgin I., Yang I.-S. Energy carries information. Int. J. of Modern Physics A, 2014, vol. 29, no. 20, art. 1450115. DOI: 10.1142/S0217751X14501152. 11. Horowitz J.M., Esposito M. Thermodynamics with continuous information flow. Physical Review X, 2014, vol. 4, art. 031015. DOI: 10.1103/PhysRevX.4.031015. 12. Renes J.M. Work cost of thermal operations in quantum and Nano thermodynamics. ArXiv, 2014. URL: https://arxiv.org/pdf/1402.3496.pdf (дата обращения: 1.08.2021). 13. Lang A.H., Fisher C.K., Mora T., Mehta P. Thermodynamics of statistical inference by cells. Physical Review Letters, 2014, vol. 113, art. 148103. DOI: 10.1103/PhysRevLett.113.148103. 14. Horowitz J.M., Sagawa T. Equivalent definitions of the quantum nonadiabatic entropy production. J. of Statistical Physics, 2014, vol. 156, no. 1, pp. 55–65. DOI: 10.1007/s10955-014-0991-1. 15. Apollaro T.J.G., Francica G., Paternostro M., Campisi M. Work statistics, irreversible heat and correlations build-up in joining two spin chains. Physica Scripta, 2015, vol. 2015, no. 165, pp. 14–23. DOI: 10.1088/0031-8949/2015/T165/014023. 16. Hemmo M., Shenker O. Entropy and computation: The Landauer-Bennett thesis reexamined. Entropy, 2013, vol. 15, no. 8, pp. 3297–3311. DOI: 10.3390/e15083297. 17. Ульянов С.В., Бархатова И., Албу В. Квантовая релятивистская информатика: логика физических противоречий корректности и строгости математических моделей квантовых релятивистских объектов. Berlin: LAP Lambert Academic Publishing, 2015. 400 c. 18. Dodonov V.V., Manko O.V., Manko V.I., Wuensche A. Energy-sensitive and ²Classical-like² distances between quantum states. Physica Scripta, 1998, vol. 59, no. 2, pp. 81–89. DOI: 10.1238/Physica.Regular.059a00081. 19. Filippov S.N., Manko V.I. Distances between quantum states in the tomographic-probability representation. Physica Scripta, 2010, no. T140, art. 014043. DOI: 10.1088/0031-8949/2010/T140/014043. 20. Gómez C. Complexity and time. Physical Review D, 2020, vol. 101, art. 065016. DOI: 10.1103/PhysRevD.101.065016. 21. Funo K., Watanabe Y., Ueda M. Thermodynamic work gain from entanglement. Physical Review A, 2013, vol. 88, art. 052319. DOI: 10.1103/PhysRevA.88.052319. 22. Toyabe S., Sagawa T., Ueda M., Muneyuki E., Sano M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nature Physics, 2010, vol. 6, no. 12, pp. 988–992. DOI: 10.1038/nphys1821. 23. Van der Meer R., Ng N.H.Y., Wehner S. Smoothed generalized free energies for thermodynamics. Physical Review A, 2017, vol. 96, art. 062135. DOI: 10.1103/PhysRevA.96.062135. 24. Tribus M., Shannon P.T., Evans R.B. Why thermodynamics is a logical consequence of information theory. AIChE J., 1966, vol. 12, no. 2, pp. 244–248. DOI: 10.1002/aic.690120208. 25. Bais F.A., Farmer J.D. The physics of information. Philosophy of Information, 2008, pp. 609–683. DOI: 10.1016/B978-0-444-51726-5.50020-0. 26. Sagawa T., Ueda M. Erratum: Minimal energy cost for thermodynamic information processing: Measurement and information erasure [Phys. Rev. Lett. 102, 250602 (2009)]. Physical Review Letters, 2011, vol. 106, art. 189901. DOI: 10.1103/PhysRevLett.106.189901. 27. Horowitz J., Sandberg H. Second-law-like inequalities with information and their interpretations. New J. of Physics, 2014, vol. 16, art. 125007. DOI: 10.1088/1367-2630/16/12/125007. 28. Sandberg H., Delvenne J.-C., Newton N., Mitter S. Maximum work extraction and implementation costs for nonequilibrium Maxwell’s demons. Physical Review E, 2014, vol. 90, art. 042119. DOI: 10.1103/PhysRevE.90.042119. 29. Haddad W.M., Chellaboina V.S., Nersesov S.G. Thermodynamics: A dynamical systems approach. USA, New Jersey, Princeton: Princeton University Press, 2005, 200 p. 30. Feng Q., W. Li. Hypoelliptic entropy dissipation for stochastic differential equations. ArXiv, 2021, art. 00544. URL: https://arxiv.org/abs/2102.00544 (дата обращения: 1.08.2021). 31. Ito S., Dechant A. Stochastic time-evolution, information geometry and the Cramer-Rao Bound. Physical Review X, 2018, vol. 10, art. 021056. DOI: 10.1103/PhysRevX.10.021056. 32. Yoshimura K., Ito S. Information geometric inequalities of chemical thermodynamics. Physical Review Research, 2020, vol. 3, art. 013175. DOI: 10.1103/PhysRevResearch.3.013175. References
|
http://swsys.ru/index.php?id=4847&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:

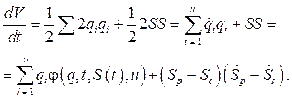
 (3)
(3)

 (4)
(4) .
. . Тогда длина геодезической линии, соединяющей состояния |ψ0〉 и |ψ1〉, определяется в виде
. Тогда длина геодезической линии, соединяющей состояния |ψ0〉 и |ψ1〉, определяется в виде


 (19)
(19)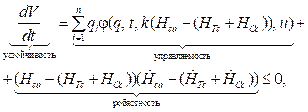 (20)
(20)


