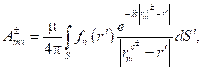Решение задачи дифракции электромагнитной волны на экранах произвольной формы с использованием технологии CUDA
| Гиниятова Д.Х. (normaliti@gmail.com) - Казанский (Приволжский) федеральный университет, Институт вычислительной математики и информационных технологий (старший преподаватель), Казань, Россия, Маркина А.Г. (m8angelina@gmail.com) - Казанский (Приволжский) федеральный университет, Институт вычислительной математики и информационных технологий (младший научный сотрудник), Казань, Россия | |
| Ключевые слова: параллельный алгоритм, rwg-функция, метод моментов, технология cuda, задача дифракции |
|
| Keywords: parallel algorithm, rwg functions, method of moments, cuda technology, diffraction problem |
|
|
|
|
Задачи дифракции электромагнитных волн на плоских металлических экранах произвольной формы возникают при исследовании самых разных электродинамических систем, например, при проектировании микрополосковых антенн со сложной формой излучателя. Для их решения необходимо использовать строгие аналитические методы прикладной электродинамики [1–3]. Для решения подобных задач также разработан ряд приближенных численных методов [4–6]. На сегодняшний день широкое распространение в специализированном ПО получили метод моментов, метод конечных элементов (FEM) и метод конечных разностей во временной области (FDTD) [7, 8]. Первые два метода обусловливают необходимость решать комплексные системы линейных алгебраических уравнений (СЛАУ), порядок которых напрямую зависит от желаемой степени точности решения задачи. Применение эффек- тивных численных методов и новых компьютерных технологий позволяет решать подобные задачи за приемлемое время. Перспективной технологией с точки зрения времени расчета являются параллельные вычисления на графическом процессоре (NVIDIA CUDA) [9–12]. В статье представлен параллельный алгоритм решения задачи дифракции на экранах произвольной формы методом моментов, реализуемый на GPU посредством технологии CUDA. Как известно, задача дифракции плоской электромагнитной волны может быть сформулирована в терминах операторного уравнения для поверхностного тока [13, 14], где в качестве оператора может выступать линейный интегральный или интегро-дифференциальный оператор, причем интегрирование ведется по всей области дифракции. Для численного решения таких уравнений используют метод моментов. Теоретические основы этого метода наиболее полно изложены в работах Харрингтона, в частности, в его монографии [15]. В русскоязычной литературе последовательное описание и анализ метода моментов даны в [16]. Современное изложение метода моментов для задач электродинамики содержится в монографиях [17] и [14]. Кроме того, есть работы, посвященные математическому обоснованию метода моментов и оценке сходимости приближенного решения к точному (например [18]). Как отмечено выше, разбиение поверхности дифракции на небольшие конечные области приводит к построению и дальнейшему численному решению СЛАУ очень высокого порядка. И в то же время этот класс задач хорошо поддается распараллеливанию, а архитектура графического процессора (GPU) хорошо оп- тимизирована для параллельной обработки данных. Для пластин со сложной геометрией триангуляция области может осуществляться с помощью любого алгоритма [19], однако для задач электродинамики требуется, чтобы треугольная сетка удовлетворяла ряду свойств, что влечет за собой уточнение работы алгоритма и значительные временные затраты. Для некоторых обладающих особенностями поверхностей, таких как гребенчатые пластины, алгоритм триангуляции можно ускорить. В настоящей работе представлен алгоритм быстрой триангуляция плоских экранов с произвольной границей с применением технологии CUDA. Кроме того, весь последующий цикл решения задачи дифракции методом моментов, а именно сборка матрицы СЛАУ, также осуществляется на GPU, что значительно ускоряет работу всего алгоритма по сравнению с последовательной версией. Постановка задачи дифракции Рассмотрим постановку задачи дифракции электромагнитной волны на идеально проводящем тонком экране произвольной формы [20]. Пусть Ω Ì R2 – ограниченная область с кусочно-гладкой границей G, состоящей из конечного числа дуг класса C∞, стыкующихся под ненулевыми углами. Задача дифракции внешнего электромагнитного поля E0, H0 на идеально проводящей пластине Ω, расположенной в свободном пространстве с волновым числом k2 = w2em, состоит в определении рассеянного электромагнитного поля:
удовлетворяющего однородным уравнениям Максвелла
граничным условиям для касательных составляющих электрического поля на поверхности пластины Et|W = – Et0|W, (3) условиям конечности энергии в любом ограниченном объеме пространства
и условиям на бесконечности
Для полного поля Htot = H0 + H. Будем предполагать, что все источники падающего поля находятся вне пластины E0 Î C¥(Wd), Wd = {x:|x – y| < d, y Î W}, (6) отсюда следует, что
Часто в качестве падающего поля рассматривают либо плоскую волну, либо электрический или магнитный диполь, расположенный вне пластины Пусть S – открытая или замкнутая поверхность идеально проводящего тела с единичной нормалью n. Через Ei обозначим электрическое поле, создаваемое источником в отсутствие тела (антенны). Оно индуцирует на S поверхностный ток J. Если S – открытая поверхность, то мы рассматриваем J как сумму поверхностных токов на противоположных сторонах S, следовательно, нормальная компонента J должна исчезать на границах S. Рассеянное поле ES при этом может быть вычислено по формуле E¢ = – iwA – ÑФ, (8) где A и F – векторный и скалярный потенциалы соответственно. Известно, что потенциалы связаны с возбуждающим током функцией Гри- на [14]. В свободном пространстве справед- ливы следующие формулы:
где функция Грина определяется формулой
Граничное условие для электрического поля в случае идеально проводящей поверхности имеет вид
откуда, использовав (8), получим интегро-дифференциальное уравнение относительно J:
Вместе с (9)–(11) уравнение (13) представляет собой так называемое интегральное уравнение для электрического поля. Иногда в литературе уравнение (13) также называют уравнением в терминах смешанных потенциалов (MPIE). Тем не менее, всюду далее будем придерживаться термина EFIE, подразумевая под ним уравнение (13) с учетом (9)–(11). Решение задачи дифракции методом моментов Широкое применение для расчета поверхностных токов, возникающих на плоских металлических или диэлектрических поверхностях при излучении в свободное пространство, получил метод моментов [14]. Примером области для моделирования этим методом может служить микрополосковая антенна, которая имеет планарную структуру, состоящую из нескольких слоев, расположенных друг над другом [21]. Фактически же метод представляет собой способ решения уравнений Максвелла, записанных в интегральной форме (EFIE). Для решения задачи (13) методом моментов исходную область разбивают на элементарные подобласти, а искомую функцию (поверхностный ток J) представляют в виде разложения по конечному числу базисных функций с неизвестными коэффициентами. Каждая базисная функция, заданная в элементарной подобласти, как правило, имеет простой вид: равна нулю вне указанной области и непрерывна на ее границе. Далее обе части исходного уравнения умножают на пробные функции и сводят задачу к решению СЛАУ относительно неизвестных коэффициентов. Основное практическое преимущество метода моментов состоит в том, что необходимо дискретизировать только ме- таллические элементы моделируемого объ- екта, а не пространство вокруг. Таким образом получается плоская сетка достаточно скромных размеров, которая меньше и проще, чем аналогичная объемная сетка, необходимая для моделирования методами FEM и FDTD. Базисные и пробные функции. Базисные и пробные функции могут быть выбраны произвольно, однако на практике их подбирают так, чтобы относительно небольшое количество базисных функций гарантировало хорошую аппроксимацию, а их свойства в достаточной степени моделировали поведение искомой функции. Для решения поставленной задачи выбраны RWG-функции, которые впервые были введены в [22]. Их удобно использовать для поиска приближенного решения EFIE, когда исходная область разбита на треугольные площадки, что, в свою очередь, обеспечивает достаточно хорошую аппроксимацию области даже сложной формы. Будем использовать стандартные термины, такие как «грань» – для обозначения поверхности элементарной треугольной площадки, «ребро» («граничное ребро») – для обозначения одной из ее сторон и «вершина» – для обозначения вершины треугольной области.
Базисная функция, ассоциированная с n-м внутренним ребром, имеет вид
где ln – длина n-го ребра; Следуя методу моментов, представим поверхностный ток всюду на S в виде приближенной формулы
где N – количество внутренних ребер. Следующим шагом в методе моментов является процедура тестирования или умножения исходного уравнения на пробные функции. Одним из наиболее эффективных является метод Галеркина, когда в качестве пробных функций выбираются те же базисные функции, что обеспечивает соблюдение граничных условий во всей области решения, а не только в отдельно взятых точках. Поэтому в качестве пробных функций также возьмем RWG-функции. Определим скалярное произведение как áf, gñ =
Использовав методы вычисления поверхностного интеграла и свойства fm на границах S, последнее слагаемое в (16) перепишем в виде
Из определения (14) следует, что
и интеграл в (17) может быть аппроксимирован следующим образом:
В (18) среднее значение F на каждом треугольнике заменили значением F в центре масс треугольников. Использовав аналогичные рассуждения, можно аппроксимировать слагаемые в (16), содержащие векторный потенциал и падающее поле. Покажем это на примере слагаемого
Таким образом, умножив обе части EFIE на пробные RWG-функции, с учетом (17)–(19) получим уравнение
которое справедливо для каждого внутреннего ребра с номером Формирование СЛАУ. После подстановки разложения поверхностного тока по базисным функциям (15) в уравнение (20) получим СЛАУ размера N´N: Z I = V, (21) где Z = [Zmn] – матрица моментов; I = [an] – столбец неизвестных коэффициентов; V = [Vm] – столбец известной правой части. Элементы матрицы Z и столбца V определя- ются по следующим формулам:
где
После вычисления элементов матрицы моментов и столбца правой части решим полученную СЛАУ (21) относительно неизвестных коэффициентов и восстановим искомую функцию J. Отметим, что матрица Z в данном случае является плотной комплексной матрицей в отличие, например, от разряженных матриц, возникающих в методе конечных элементов. Алгоритм решения на GPU Параллельные алгоритмы решения задачи дифракции на прямоугольных и гребенчатых пластинах предложены в [23]. Рассмотрим алгоритм решения для экранов произвольных форм, граница которых задана как набор последовательных сегментов. Численное решение поставленной задачи условно можно разделить на три логических этапа. На первом этапе построим треугольную сетку, покрывающую поверхность исходной области. На ee основе сформируем массив RWG-элементов (пар треугольников с общим внутренним ребром) и вычислим дополнительные геометрические характеристики. На втором этапе вычислим элементы матрицы моментов и столбца правой части СЛАУ по формулам (22) и (23). Наконец, на третьем этапе решим СЛАУ, а функцию J восстановим по уже известным коэффициентам разложения согласно формуле (20). Остановимся подробнее на первых двух этапах. Триангуляция. Как уже отмечено, на свойства треугольной сетки, покрывающей исходную область дифракции, накладывается ряд ограничений, а именно, длина сторон треугольников должна быть сопоставима с длиной падающей волны, поэтому следует избегать слишком вытянутых треугольников, а при фор- мировании RWG-элементов каждый треугольник T+ должен быть соединен с треугольниками T– посредством внутренних смежных ребер и, наоборот, каждый треугольник T– должен быть окружен треугольниками T+. Опишем быстрый алгоритм триангуляции области дифракции посредством технологии CUDA.
На основе полученной треугольной сетки на GPU сформируем массив RWG-элементов и вычислим сопутствующие геометрические характеристики, необходимые для вычисления интегралов в (22), (23) и формирования матрицы моментов. Матрица моментов. Следующим этапом является вычисление элементов матрицы моментов и правой части СЛАУ по формулам (22) и (23). Именно этот этап алгоритма наиболее трудоемкий и затратный по времени. Рассмотрим алгоритм вычисления произвольного элемента матрицы моментов. Для этого выберем элемент zij, построенный на паре RWG-элементов с номерами i и j. В данном случае интегрирование ведется по паре треугольников Tj+ и Tj–, а подынтегральная функция содержит множитель 1/|r – rc±|, где r – точка, принадлежащая треугольникам Tj+ и Tj–, а rc± – центр масс треугольников Ti+ и Ti– соответственно. В случае, когда i ≠ j, можно использовать следующий метод приближенного интегрирования.
Когда RWG-элементы пересекаются по одному из треугольников или полностью совпадают (например, при вычислении элемента zii), возникает ситуация, приводящая к делению на нуль. Чтобы этого избежать, в квадратурной формуле можно использовать не центры масс, а так называемые «смещенные» центры масс. Их можно рассчитать как середину средней ли- нии, параллельной диагональному ребру треугольника (см. рис. 7в). Тогда деление на нуль не возникнет. Для построения всей матрицы моментов требуется произвести перебор по всем RWG-элементам. Напомним, что размер исходной матрицы зависит от размера треугольной сетки и равен N×N, где N – количество RWG-элементов. Согласно (27) и (28), каждый элемент матрицы и правая часть могут быть вычислены независимо, поэтому каждая CUDA-нить исполняемого ядра, отвечающая за сборку матрицы моментов, вычисляет соответствующий элемент параллельно с другими ни- тями. На этом этап формирования матрицы СЛАУ можно считать завершенным. Полученная СЛАУ может быть решена методом Гаусса или одним из итерационных методов. Численные результаты Для расчета токов на экране заданной формы был написан программный модуль на языке программирования С++, содержащий визуализатор триангуляции, реализованный на SFML. Код для исполнения на графическом процессоре написан на языке C/CUDA, предоставляемом NVidia с поддержкой CUDA API для компиляции кода, исполняемого на GPU. При запуске основного вычислительного ядра, отвечающего за расчет элементов матрицы моментов, были использованы двумерная сетка блоков и двумерные блоки нитей. Такой подход удобен тем, что матрица моментов представляется в памяти в виде двумерного массива данных. Для запуска программы был использован ноутбук с процессором Intel Core i5-8265U (1,8 ГГц), оперативной памятью 8 ГБ и графическим устройством GeForce MX250, операционная система – Fedora Linux 35. Рассмотрен случай нормального падения электромагнитной волны с длиной, равной λ. Представленные ниже расчеты выполнены для плоских экранов различной формы: квадратной пластины со стороной, равной λ, и правильного восьмиугольника, вписанного в окружность радиуса λ.
На рисунке 9 представлены графики распределения абсолютных значений составляющей тока |Jx| на поверхности правильного восьми- угольника, вписанного в окружность с радиусом, равным длине волны, вдоль линии А, параллельной оси OX с различным уровнем дискретизации области: 165, 281 и 617 RWG-элементов соответственно. Чем ниже частота дискретизации, тем более грубую аппроксимацию площади мы получим (то есть увеличивается площадь исходного экрана). Все три распределения построены по точкам, лежащим внутри исходной области
Заключение Предложен алгоритм решения задачи дифракции электромагнитных волн на плоском металлическом экране произвольной формы. Задача сведена к решению интегрального уравнения электрического поля (EFIE) методом моментов. В качестве базисных и пробных функций использованы одни и те же RWG-функции, что соответствует идее метода Галеркина. Подробно обсуждены два основных этапа численного алгоритма – триангуляция исходной области с последующим формированием массива RWG-элементов и вычисление элементов матрицы моментов. Для параллельной реализации алгоритма использована технология CUDA. Предложен и реализован простой и быстрый алгоритм триангуляции на GPU для экранов различной формы. Самый трудоемкий этап – заполнение матрицы моментов – также реализован на графическом процессоре. Получено 20-кратное ускорение работы алгоритма на видеокарте. Приведены численные результаты для квадратной и восьмиугольной металлических пластин с различной степенью дискретизации. Полученные графики показали хорошее соответствие с результатами предыдущих работ. Таким образом, предложенный параллельный алгоритм может быть использован для ускорения проектирования антенн различной формы [24], а также для решения задач дифракции плоских электромагнитных волн на экранах с произвольными границами. Работа выполнена за счет средств Программы стратегического академического лидерства Казанского (Приволжского) федерального университета («ПРИОРИТЕТ-2030»). Литература 1. Nagasaka T., Kobayashi K. Wiener–Hopf analysis of the plane wave diffraction by a thin material strip. IEICE Transactions on Electronics, 2017, vol. E100C, no. 1, pp. 11–19. DOI: 10.1587/transele.E100.C.11. 2. Luz E., Granot E., Malomed B.A. Analytical boundary-based method for diffraction calculations. J. of Optics, 2019, vol. 22, no. 2, art. 025601. DOI: 10.1088/2040-8986/ab60c1. 3. Nethercote M.A., Assier R.C., Abrahams I.D. Analytical methods for perfect wedge diffraction: A review. Wave Motion, 2020, vol. 93, art. 102479. DOI: 10.1016/j.wavemoti.2019.102479. 4. Tumakov D.N., Tukhvatova A.R. Diffraction of an electromagnetic wave by gaps between plates. Lobachevskii J. of Mathematics, 2012, vol. 33, no. 4, pp. 364–373. DOI: 10.1134/S1995080212040051. 5. Tumakov D.N. Iterative method for solving the problem of scattering of an electromagnetic wave by a partially shielded conducting sphere. Applied Mathematical Sciences, 2014, vol. 8, no. 118, pp. 5887–5898. DOI: 10.12988/AMS.2014.48657. 6. Selezov I.T., Kryvonos Y.G., Gandzha I.S. Some analytical and numerical methods in the theory of wave propagation and diffraction. In: Wave Propagation and Diffraction. Foundations of Engineering Mechanics. Springer Publ., Singapore, 2018, pp. 1–24. DOI: 10.1007/978-981-10-4923-1_1. 7. Shibata K., Kobayashi M. Difference between the method of moments and the finite element method for estimation of complex permittivity in liquids using a coaxial probe. Proc. Int. Symposium EMC, 2019, pp. 100–105. DOI: 10.1109/EMCEurope.2019.8871604. 8. Taflove A., Hagness S. Computational Electrodynamics: The Finite-Difference Time-Domain Method. Artech House Publ., Norwood, 2000, 1038 p. 9. Молостов И.П., Щербинин В.В. Применение технологии NVIDIA CUDA для численного моделирования распространения электромагнитных импульсов // Изв. АлтГУ. 2015. T. 85. № 1. С. 39–43. DOI: 10.14258/izvasu(2015)1.1-06. 10. Zhang Y., Mei X., Lin H. OpenMP-CUDA accelerated moment method for homogeneous dielectric objects. Proc. IEEE APSURSI, 2014, pp. 1634–1635. DOI: 10.1109/APS.2014.6905143. 11. Li J., Zhang Z., Zheng K., Wu C., Gao S. GPU accelerated non-illuminated graphical electromagnetic computing method with high accuracy. Optik, 2017, vol. 142, pp. 523–528. DOI: 10.1016/J.IJLEO.2017. 05.104. 12. Peng S., Nie Z.P. Acceleration of the method of moments calculations by using graphics processing units. IEEE Transactions on Antennas and Propagation, 2008, vol. 56, no. 7, pp. 2130–2133. DOI: 10.1109/TAP.2008.924768. 13. Balanis C.A. Antenna Theory: Analysis and Design. John Wiley & Sons Publ., NY, 2016, 1095 p. 14. Gibson W.C. The Method of Moments in Electromagnetics. Chapman and Hall/CRC Publ., NY, 2007, 288 p. DOI: 10.1201/9781420061468. 15. Harrington R.F. Field Computation by Moment Methods. Wiley-IEEE Press, 1993, 240 p. DOI: 10.1109/9780470544631. 16. Никольский В.В. Вариационные методы для внутренних задач электродинамики. М.: Наука, 1967. 460 с. 17. Sadiku M.N. Elements of Electromagnetics. Oxford University Press, NY, 2001, 896 p. 18. Mittra R., Klein C.A. Stability and convergence of moment method solutions. In: Topics in Applied Physics, pp. 129–163. DOI: 10.1007/3540070729_26. 19. De Loera J.A., Rambau J., Santos F. Triangulations: Structures for Algorithms and Applications. Springer Publ., Berlin, 2010, 534 p. 20. Смирнов Ю.Г., Медведик М.Ю., Максимова М.А. Решение задачи дифракции электромагнитной волны на экранах сложной формы // Изв. высших учебных заведений. Поволжский регион. Физико-математические науки. 2012. № 4. C. 59–72. 21. Tumakov D., Markina A., Badriev I. Fast method for designing a well-matched symmetrical four-tooth-shaped microstrip antenna for Wi-Fi applications. J. of Physics: Conf. Ser., 2019, vol. 1158, 042029. DOI: 10.1088/1742-6596/1158/4/042029. 22. Rao M.S., Wilton R.D., Glisson A.W. Electromagnetic scattering by surfaces of arbitrary shape. IEEE Transactions on Antennas and Propagation, 1982, vol. 30, no. 3, pp. 409–418. DOI: 10.1109/TAP.1982. 1142818. 23. Giniyatova D., Tumakov D., Markina A. Solving problem of electromagnetic wave diffraction by a metal plate using CUDA. Proc. IEEE EWDTS, 2020, pp. 324–329. DOI: 10.1109/EWDTS50664. 2020.9224674. 24. Markina A., Tumakov D. Designing the four-tooth-shaped microstrip antenna for Wi-Fi applications. Proc. Int. Conf. SUMMA, 2019, pp. 25–30. DOI: 10.1109/SUMMA48161.2019.8947603. References
|
http://swsys.ru/index.php?id=4912&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Программный комплекс оптимизации законов управления
- Применение MATLAB/GNU Octave для расчета погонных параметров многопроводных линий передачи методом моментов
- Применение технологии CUDA для симуляции частиц при параллельном программировании
- Реализация некоторых приложений проекта Mantevo на платформе OpenTS DMPI
- Реализация алгоритма оптимизации параметров молекулярно-динамического потенциала REAXFF


 (14)
(14)
 (18)
(18) (19)
(19) (20)
(20)