Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Ключевое слово: |
|
| Page views: 15255 |
Print version Full issue in PDF (1.18Mb) |
Рассмотрим базовую сетевую модель проекта ²работы на дугах², то есть ориентированный граф Предположим, что для каждой операции проекта - вероятностная оценка: продолжительность операции - имеется интервальная неопределенность относительно продолжительности операции: - имеется нечеткая информация относительно продолжительности: В классическом подходе на базе метода критического пути неопределенность относительно продолжительности операций учитывается менеджером проекта (или исполнителем конкретной операции) при выборе вероятностной оценки продолжительности. При этом каждая работа содержит резерв времени для выполнения операции При интервальной оценке или нечеткой продолжительности операции резерв выполнения также содержится в оценке Предложим другой вариант учета неопределенности относительно продолжительности операций, основанный на идее использования буферов в графике проекта (например [2-4]). Для этого отделим резервы, заложенные в каждой работе проекта, и соберем (агрегируем) их в буферах двух типов, размещенных в следующих местах на графике проекта: · буфер проекта (БП) размещается сразу после последней операции критического пути; продолжительность БП равна агрегированной оценке продолжительности резервов работ, лежащих на критическом пути проекта:
· обеспечивающие буферы (ОБ) размещаются после последовательности некритических работ, непосредственно примыкающих к работе на критическом пути (обеспечивающие цепочки – оц); продолжительность ОБ равна агрегированной оценке продолжительности резервов операций, составляющих ОЦ.
При решении задачи календарного планирования перед менеджером проекта ставится задача построения календарного графика – определения последовательности выполнения, сроков, начала и окончания операций – с учетом ограничений (технологические связи, доступность ресурсов) и неопределенности (оценка продолжительности работ), другими словами, задача: · выбора ²нижней² оценки для продолжительности операций – · выбора оптимального (с точки зрения продолжительности и стоимости) способа агрегирования резервов в БП и ОБ – определение продолжительности буферов – · определения планируемой даты завершения проекта с учетом неопределенности – срока завершения БП (уточним, что реальная продолжительность проекта может быть меньше, в случае неполного использования БП) – Необходимо отметить, что при размещении буферов критический путь в графике проекта может измениться, что необходимо учесть при определении продолжительности проекта. В ходе реализации проекта с возникновением задержки при выполнении операции, лежащей на критическом пути, планируемые сроки завершения следующих за ней операций смещаются за счет использования БП без нарушения запланированной даты завершения проекта. С возникновением задержки при выполнении работы одной из ОЦ планируемые сроки завершения следующих за ней операций смещаются за счет использования ОБ, не оказывая влияния на планируемое начало следующей за ОБ критической операции.
В [5] был предложен метод дихотомического программирования для оптимизации проекта по стоимости. Рассмотрим задачу определения оптимальной продолжительности буферов, агрегированных из резервов работ для оптимизации проекта по стоимости. Сначала рассмотрим простой случай, когда сетевой график представляет собой последовательную цепочку работ. Примем, что зависимость стоимости работ от продолжительности является линейной для каждой работы:
Здесь Согласно предложенной гипотезе, для оценки продолжительности последовательности работ используем минимальную продолжительность отдельных работ и агрегируем в БП доступные резервы. БП в данном случае добавляется после завершающей работы последовательности.
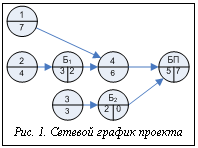
Если полученный срок завершения проекта не удовлетворяет требуемому сроку ( Сокращение продолжительности буфера проекта, естественно, потребует увеличения затрат. Задача заключается в сокращении продолжительности БП таким образом, чтобы проект был реализован в требуемые сроки, а дополнительные затраты были минимальными. Если сетевой график проекта имеет более сложную структуру и в нем выделен критический путь и цепочки некритических работ, непосредственно предшествующих работам на критическом пути, то, кроме БП, добавляются ОБ. Алгоритм нахождения оптимальной длительности БП рассмотрим на примере проекта, сетевой график которого изображен на рисунке 1. В таблице приведены значения продолжительности и стоимости реализации отдельных работ и буферов. Таблица Данные по работам и буферам в примере
Шаг 1. Отметим, что сетевой график имеет агрегируемый вид, в противном случае необходимо привести график к этому виду [5]. По этому сетевому графику может быть построено дерево агрегирования, которое определяет дихотомическое представление функции продолжительности проекта Шаг 2. Упростим дихотомическое представление продолжительности проекта. Так как работы {1-4} имеют фиксированную продолжительность, то могут быть выполнены операции сложения для упрощения дерева (значения введенных переменных Шаг 3. Построение таблиц дихотомического представления типа дерева (рис. 4) производится в соответствии с процедурой, предусмот- ренной методом дихотомического программирова- ния [5].
Шаг 4. В таблице Z4 выделим ячейку со значением продолжительности Шаг 5. В таблице Z3 выделим ячейку со значением продолжительности 14, соответствующую минимальной суммарной стоимости. В приведенном примере – это ячейка 14/69, ей соответствуют значения продолжительности переменной Шаг 6. В таблице Z2 значению продолжительности 13 соответствует ячейка 13/43, ей соответствует значение продолжительности 7 из таблицы Z1. Шаг 7. В таблице Z1 выделим ячейку со значением продолжительности 7, соответствующую минимальной суммарной стоимости. В приведенном примере – это ячейка 7/34, ей соответствует значение продолжительности переменной Для значений буферов Б1, Б2, БП получены следующие оценки продолжительности и соответствующих затрат:
Продолжительность проекта при этом равна
В настоящей работе рассмотрена модель проекта, учитывающая неопределенность относительно продолжительности выполнения работ. Предложен вариант агрегирования резервов отдельных работ во временные буферы, размещенные в различных точках сетевого графика проекта. На основе метода дихотомического программирования предложен метод решения задач оптимизации использования финансовых ресурсов при календарном планировании с учетом неопределенности относительно продолжительности работ. В качестве перспективных направлений дальнейших теоретических исследований можно выделить: расширение модели проекта для различных способов задания неопределенности (интервальная оценка, нечеткая оценка); разработки метода оценки хода выполнения работ на основе предложенной модели буферов в проекте. Список литературы 1. Бурков В.Н., Новиков Д.А. Как управлять проектами. – М.: Синтег-Гео, 1997. 2. Goldratt, E. M., Critical Chain, Great Barrington, MA: North River Press, 1997. 3. Lawrence P. Leach. Critical chain project management. ARTECH HOUSE, INC. Norwood, 2000. 4. S.Van de Vonder, E.Demeulemeester, W.Herroelen, R. Leus. The Use of Buffers in Project Management: The Trade-off between Stability and Makespan. Department of Applied Economics, K.U.Leuven, Belgium, 2004. 5. Буркова И.В. Метод дихотомического программирования в задачах управления проектами. Дисс... канд. технич. наук. - М., 2004. |
| Permanent link: http://swsys.ru/index.php?id=494&lang=en&page=article |
Print version Full issue in PDF (1.18Mb) |
| The article was published in issue no. № 4, 2005 |
Perhaps, you might be interested in the following articles of similar topics:
- Эвристические и точные методы программной конвейеризации циклов
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Интеллектуальная поддержка реинжиниринга конфигураций производственных систем
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам
- Система поддержки принятия решений по планированию профессиональной структуры подготовки специалистов
Back to the list of articles
 без контуров. В графе
без контуров. В графе  – дуги сети соответствуют операциям;
– дуги сети соответствуют операциям;  – вершины соответствуют событиям (моменты начала/окончания одной или нескольких операций) [1].
– вершины соответствуют событиям (моменты начала/окончания одной или нескольких операций) [1]. задана продолжительность
задана продолжительность  – время, требуемое для ее завершения. Продолжительность операции может быть задана одним из следующих способов:
– время, требуемое для ее завершения. Продолжительность операции может быть задана одним из следующих способов: определяется значением функции распределения при заданном значении вероятности;
определяется значением функции распределения при заданном значении вероятности;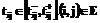 ;
;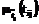 , где
, где  – функция принадлежности нечеткой продолжительности операции.
– функция принадлежности нечеткой продолжительности операции. , который позволяет соблюдать запланированную дату окончания работы даже при задержке выполнения операции.
, который позволяет соблюдать запланированную дату окончания работы даже при задержке выполнения операции.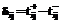 .
. ,(1)
,(1) (2)
(2) ;
; ;
;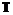 .
. Оптимизация БП по стоимости
Оптимизация БП по стоимости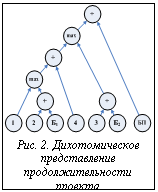
 .
. ;
;  – минимально возможная продолжительность работы;
– минимально возможная продолжительность работы;  – максимальная;
– максимальная;  – коэффициент увеличения стоимости проекта при уменьшении продолжительности
– коэффициент увеличения стоимости проекта при уменьшении продолжительности  -й работы. Зафиксируем продолжительность всех работ, равную минимальным оценкам:
-й работы. Зафиксируем продолжительность всех работ, равную минимальным оценкам: 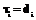 .
.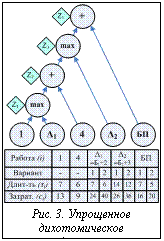 Предположим, что продолжительность добавленного БП
Предположим, что продолжительность добавленного БП 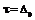 , тогда продолжительность всего проекта
, тогда продолжительность всего проекта  определяется длиной критического пути (в данном случае совпадает с продолжительностью последовательности работ) и равна
определяется длиной критического пути (в данном случае совпадает с продолжительностью последовательности работ) и равна 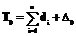 . Стоимость проекта в данном случае зависит от стоимости выполнения отдельных работ и от продолжительности буфера. Так как в рассматриваемом подходе были выбраны и зафиксированы минимальные значения продолжительности отдельных работ, то стоимость выполнения проекта равна
. Стоимость проекта в данном случае зависит от стоимости выполнения отдельных работ и от продолжительности буфера. Так как в рассматриваемом подходе были выбраны и зафиксированы минимальные значения продолжительности отдельных работ, то стоимость выполнения проекта равна  .
.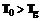 ), то необходимо принять меры к сокращению продолжительностей буфера проекта так, чтобы длина критического пути с учетом буфера проекта была не больше
), то необходимо принять меры к сокращению продолжительностей буфера проекта так, чтобы длина критического пути с учетом буфера проекта была не больше 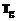 .
.
 (рис. 2).
(рис. 2). приведены на рис. 3).
приведены на рис. 3).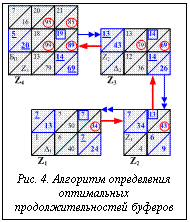 Для оценки результата применения алгоритма рассмотрим решение для достижения минимального уровня затрат при требуемой продолжительности проекта
Для оценки результата применения алгоритма рассмотрим решение для достижения минимального уровня затрат при требуемой продолжительности проекта  .
. , соответствующую минимальной агрегированной стоимости работ проекта. В приведенном примере – это ячейка 19/89, ей соответствуют значения продолжительности 14 из таблицы Z3 и 5 для продолжительности БП.
, соответствующую минимальной агрегированной стоимости работ проекта. В приведенном примере – это ячейка 19/89, ей соответствуют значения продолжительности 14 из таблицы Z3 и 5 для продолжительности БП. и значение продолжительности 13 из таблицы Z2.
и значение продолжительности 13 из таблицы Z2. .
. (3)
(3) , а стоимость выполнения работ проекта с учетом неопределенности соответственно равна
, а стоимость выполнения работ проекта с учетом неопределенности соответственно равна
