Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: V.B. Tarasov (vbulbov@yahoo.com) - Bauman Moscow State Technical University (Associate Professor), Moscow, Russia, Ph.D, Afonin P.V. (pavlafon@yandex.ru) - Bauman Moscow State Technical University, Moscow, Russia, Ph.D, () - | |
| Ключевое слово: |
|
| Page views: 18947 |
Print version Full issue in PDF (1.41Mb) |
В работе предлагается модель формирования различных структур виртуальных предприятий, разработанная на основе анализа возможных видов взаимодействия между партнерами. Объединение (альянс) предприятий рассматривается как популяция эволюционирующих агентов, то есть эволюционирующая многоагентная система (ЭМАС) с определенным набором параметров. Основу модели составляет эволюционный алгоритм, использующий модифицированные генетические операторы. При этом ставится задача нахождения эффективных структур объединений предприятий. В плане функционирования ЭМАС эволюционный алгоритм выполняет роль некоторого вышестоящего координатора, накладывающего ограничения на деятельность всей популяции агентов. Анализ результата наложения этих ограничений позволяет накапливать в популяции положительные свойства и формировать наиболее подходящие под конкретные условия структуры объединений предприятий. Формализованное представление модели Рассматриваемое сообщество предприятий представляется в виде ЭМАС: EMAS = {A1, A2, …, Ai, …, An}. Каждый i-й агент системы характеризуется набором параметров: Ai=(ai1, ai2, ai3, ai4). Для решения задачи требуется, используя подходящие эволюционные (генетические) операторы, сформировать организационные структуры, наилучшим образом удовлетворяющие внутреннему состоянию и намерениям каждого агента. Образованию каждой организационной структуры предшествует создание нового члена популяции (порождение потомка агентами, образующими объединение). Таким образом, множество агентов популяций можно разделить на два подмножества:
где Появление i-го потомка связано с взаимодействием его родителей: Эволюционные операторы представляются четверкой кооперативных видов взаимодействия: EvO={As, Comb, SI, Mer}, где As – оператор типа “ассоциация” (агенты на паритетных началах участвуют в создании нового агента); Comb – оператор типа “комбинация” (один из агентов имеет приоритет, поскольку является владельцем большего из ресурсов); SI – оператор типа “селективное объединение” (агенты являются недостающими дополнениями друг друга для создания нового сильного агента); Mer – эволюционный оператор типа “слияние” (исходные агенты, объединяются и теряют свою самостоятельность, ею обладает только созданный агент). Задачу порождения нового агента можно представить следующим образом. Для порождения нового агента необходимо наличие пары агентов-родителей, удовлетворяющих определенным ограничениям (условиям взаимодействия). При этом процесс порождения потомка определяется следующими четырьмя факторами: - вкладываемые родителями ресурсы в потомка: равномерно/неравномерно; - характер отношений между родителями: паритетные/неравные; - тип стимуляции: внутренняя/внешняя; - сохранение индивидуальности и самостоятельности родителей: да/нет. В результате использования установленных схем взаимодействия (они же эволюционные операторы), сопровождающихся порождением новых членов популяции, формируется множество различных структур объединений S: S={S1, S 2, …, Si, …, Sl}. Описание некой синтезированной структуры Si представляется как: Si = {Сi, Ri} , где Сi – множество компонентов структуры (формирующих ее агентов); Ri – множество связей между компонентами структуры. Описание элементов модели Основной проблемой в генетическом алгоритме является выбор способов кодирования исходной информации. В качестве исходного объекта в модели выступает предприятие. Предприятие есть агент, который представляется в виде особи популяции (хромосомы), состоящей из набора генов. Количество генов в хромосоме для всех агентов одинаково и равно четырем. Гены имеют числовые значения, любой ген может принимать значение только из интервала от 0 до 1, включая границы. Каждая позиция (локус) в хромосоме отвечает за определенную характеристику, поэтому перестановка генов внутри одной хромосомы невозможна. Таким образом, каждый агент является индивидуальным и характеризуется своей хромосомой с конкретными значениями генов. В качестве генетических операторов приняты виды взаимодействий между агентами. Модель предлагает четыре возможных вида взаимодействия, они представлены как схемы порождения потомка, (то есть операторы скрещивания). Модель организована таким образом, что в одной схеме взаимодействия одновременно могут участвовать только два агента (две особи), а это означает, что у каждого нового агента ровно два агента-родителя. Для каждой из четырех схем взаимодействия существуют необходимые условия срабатывания, то есть далеко не каждая пара особей способна вступить во взаимодействие. Для того чтобы пара агентов имела возможность приступить к взаимодействию, необходимо, чтобы их генотипы удовлетворяли условиям срабатывания одной заданной схемы. В модели введено понятие эффективности пары. Понятно, что для каждой схемы взаимодействия существуют такие хромосомы, которые будут считаться предпочтительнее других для взаимодействия, так как значения их генов удовлетворяют условиям срабатывания в большей степени и дают наиболее желаемый результат. Поэтому эффективность пары есть характеристика, которая показывает, насколько пара взаимодействующих агентов близка к наиболее предпочтительным хромосомам для конкретной схемы. Эффективность пары подсчитывается только в том случае, если гены агентов удовлетворюет всем условиям срабатывания для конкретной схемы. К взаимодействию приступает пара агентов, обладающая наибольшим значением эффективности. Следует отметить, что для простоты, все значения параметров генотипа имеют относительные значения, то есть предполагается, что конкретные показатели предприятия были преобразованы к такому виду с помощью неких математических зависимостей или, например, получены с помощью экспертов. Каждый ген может принимать значение на интервале 0…1,0. В качестве первого гена a1 принят внутренний ресурс, которым обладает агент. Второй ген a2 показывает, какую долю от объема собственного ресурса a1 готов предоставить агент для создания нового предприятия, взаимодействуя по одной из схем. Третий ген a3 указывает на желаемую степень лидерства агента в новом образовании. И, наконец, четвертый ген a4 выражает, что служит побуждением для агента к взаимодействию. Генетический оператор (оператор скрещивания) отражает схему взаимодействия между агентами. Предложено четыре схемы возможных взаимодействий, в каждой схеме определен свой уникальный набор условий срабатывания. Результатом выполнения схемы является новая организационная структура, формируемая из агентов, вступивших во взаимодействие по данной схеме. Для описания схем введены следующие обозначения: Ai, Aj – агенты, участвующие в схеме (родители); {ai1 , ai2 , ai3 , ai4} – гены агента Ai; {a*i1, a*i2, a*i3, a*i4} – гены агента Ai после осуществления схемы взаимодействия. Изменения в генах родителей в результате взаимодействия определяются следующим образом:
Эти выражения являются первой частью генетических операторов скрещивания. Первая часть одинакова у всех четырех схем, поскольку связана лишь с изменениями в генах родителей; мы будем называть ее общей частью оператора скрещивания. Вторая часть операторов скрещивания связана с формированием потомка, и поэтому будет уникальной для каждой схемы взаимодействия: Ak – агент, возникающий в результате осуществления схемы (потомок); E – эффективность пары, зависящая от параметров еi, значения которых определяются в зависимости от удовлетворения одному из условий срабатывания схемы. Модели взаимодействий агентов Взаимодействия по сценарию ассоциации происходят добровольно, на основе согласования собственных потребностей и целей агентов, когда положительные взаимодействия между ними симметричны и носят характер координационных связей, а количество вкладываемых ресурсов соизмеримо. Оба предприятия на паритетных началах участвуют в процессе интеграции. Формой интеграции предприятий является виртуальная ассоциация – договорное объединение предприятий, создаваемое для совместного выполнения различных функций в целях постоянной координации деятельности. В такой организации взаимодействие с другими внешними органами и выход из ассоциации осуществляются в одностороннем порядке, без согласования с партнерами по ассоциации. Примером из жизни служат Ассоциация промышленных предприятий России, Ассоциация банков России и прочие объединения. В отличие от предыдущего случая, взаимодействия по схеме комбинации происходят на основе несимметричных связей между агентами. Одно предприятие имеет существенно больше ресурсов, чем другое, а отношения между ними являются иерархическими (то есть преобладают процессы субординации). В пределе один агент может заблокировать деятельность второго. Возможно несколько форм объединений по данной схеме. Виртуальная корпорация – это форма объединения удаленных друг от друга предприятий одной или нескольких отраслей на основе частичной централизации функций научно-технического и производственного сотрудничества, а также инвестиционной, финансовой, внешнеэкономической и другой деятельности. Партнеры делегируют корпорации выполнение части своих функций – тех, которые не могут выполнить сами, или тех, централизация которых дает дополнительный экономический эффект. Участники корпорации сохраняют юридическую самостоятельность. Стоит отметить, что один из участников, входящих в состав корпорации, имеет незначительный приоритет над остальными участниками. Виртуальный концерн – уставное объединение предприятий промышленности, научных организаций, транспорта, банков, торговли и т.д. на основе полной финансовой зависимости от одного или группы предпринимателей с явным лидерством одного из взаимодействующих. Виртуальный холдинг – специфическая организационная форма объединения капиталов. Подобное объединение образуется, когда акционерное общество (товарищество) само непосредственно не занимается производственной деятельностью, а лишь использует свои финансовые средства для приобретения контрольных пакетов акций других акционерных фирм с целью финансового контроля за их работой и получения дохода на вложенный в акции капитал. Селективное объединение представляет собой формирование нового агента в результате отбора элитных родителей, то есть таких предприятий, которые наиболее приспособлены по отношению к конкретным внешним воздействиям среды. Агенты в этом случае объединяются под конкретную задачу для ее решения. Виртуальный консорциум есть вариант такого объединения, обычно это сеть географически удаленных друг от друга предприятий, позволяющая объединить человеческие, финансовые научно-технические, производственные и прочие ресурсы в интересах реализации крупных программ или выполнения инновационных проектов. Предприятия, вступающие в консорциум, сохраняют свою хозяйственную самостоятельность. Такое объединение создается на время, и после выполнения поставленной задачи консорциум прекращает свое существование. В результате взаимодействия по схеме слияния исходные агенты теряют свою самостоятельность (индивидуальность) и из них формируется новая система – виртуальный трест – наиболее “сильная” форма объединения, при которой все стороны деятельности входящих в него организаций объединяются, а сами организации теряют юридическую и хозяйственную самостоятельность. |
| Permanent link: http://swsys.ru/index.php?id=501&lang=en&page=article |
Print version Full issue in PDF (1.41Mb) |
| The article was published in issue no. № 2, 2006 |
Perhaps, you might be interested in the following articles of similar topics:
- Гибридная система поиска решений на основе временных продукционных правил
- Формирование программ развития больших систем административно-организационного управления
- Оптимизация обработки информационных запросов в СУБД
- Знания в интеллектуальных системах
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам
Back to the list of articles
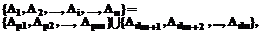
 – множество родителей;
– множество родителей; 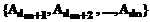 – множество потомков.
– множество потомков. , где
, где 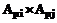 – агенты-родители, принадлежащие множеству родителей;
– агенты-родители, принадлежащие множеству родителей;  – агент-потомок, относящийся к множеству потомков; EvO – эволюционный оператор (оператор скрещивания).
– агент-потомок, относящийся к множеству потомков; EvO – эволюционный оператор (оператор скрещивания). ,
, 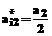 ,
,  ,
, 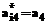 .
.