Интеграция методов обучения с подкреплением и нечеткой логики для интеллектуальных систем реального времени
| Еремеев А.П. (eremeev@appmat.ru) - Национальный исследовательский университет «Московский энергетический институт» (профессор), г. Москва, Россия, доктор технических наук, Сергеев М.Д. (SergeevMD@mpei.ru) - Национальный исследовательский университет «Московский энергетический институт» (аспирант), Москва, Россия, Петров В.С. (PetrovVS@mpei.ru) - Национальный исследовательский университет «Московский энергетический институт» (студент), Москва, Россия | |
| Ключевые слова: поддержка принятия решений, реальное время, интеллектуальная система, нечеткая логика, обучение с подкреплением, искусственный интеллект |
|
| Keywords: decision support, real time, intellectual system, fuzzy logic, time, reinforcem ent learnin, artificial intelligence |
|
|
|
|
Введение. Возможности создания интегрированной среды, объединяющей методы обучения с подкреплением (reinforcement learning, RL), гибкие алгоритмы поиска решения (anytime algorithms) и мультиагентный подход, а также применение БД NO-SQL уже были рассмотрены в [1, 2]. Выявлена перспективность интеграции в интеллектуальные системы поддержки принятия решений реального времени (ИСППР РВ), ориентированных на динамические предметные/проблемные области, искусственных нейронных сетей (ИНС) и RL-обу- чения на основе временных (темпоральных) различий (temporal differences, TD). Основные положения RL-обучения изложены в [3]. В данной работе показаны возможности применения нечеткой логики в методах обучения с подкреплением, представлены разработка соответствующих программных средств и результаты компьютерного моделирования на ряде типовых задач. RL-обучение с учетом временных различий: эффективный подход к обучению с подкреплением В работе [1] продемонстрировано, что одним из наиболее эффективных подходов к обучению с подкреплением в ИСППР РВ с учетом критерия «временные затраты–качество обучения» является RL-обучение на основе темпоральных различий (TD-обучение). Процесс обучения основан на опыте, полученном при взаимодействии агента с окружающей средой без необходимости предварительного знания о ней. Разработанные для многомерных временных рядов TD-методы обладают способностью обновлять расчетные оценки без ожидания окончательного результата, что делает их самонастраиваемыми. Особенно полезны они в динамических предметных областях и ИСППР РВ семиотического типа. Такие системы способны адаптироваться и подстраиваться к из- менениям в управляемом объекте и окружающей среде [1, 4]. В наиболее простом TD-методе TD(0) функция ценности (оценка) рассчитывается по следующей формуле:
где Vst – оценка функции ценности нетерминального состояния st в момент времени t; rt + 1 – полученное вознаграждение на текущем шаге; α – длина шага; γ – ценность терминального состояния. Важно отметить, что TD-методы дают свои оценки, частично основываясь на предыдущих, что позволяет им самонастраиваться. Преимущества TD-методов в том, что они не требуют знания модели окружающей среды, включая вознаграждения и вероятностное распределение последующих состояний, а также могут оценивать выгоду уже на следующем временном шаге, не ожидая завершения всего эпизода. Даже в случае длительных эпизодов процесс обучения не замедляется. Известно, что TD-алгоритм для любой заданной стратегии π сходится к функции V в среднем при использовании постоянного шага и в пределе сходится с вероятностью 1, если длина шага уменьшается в соответствии с условиями стохастической аппроксимации:
В работе [4] показано, что одним из важнейших достижений в области обучения с подкреплением является развитие управления с использованием TD-метода с разделенной оценкой ценности стратегий, известного как Q-обучение [5, 6]. Простейшая форма этого подхода, известная как одношаговое Q-обучение, определяется как
где Q(st, at) – оценка функции ценности после перехода из нетерминального состояния s при действии a в момент времени t. Если состояние st + 1 является терминальным, значение Q(st + 1, at + 1) полагается равным нулю. Схема алгоритма Q-обучения имеет следующий вид: Инициализировать Q(s, a) произвольно Повторять (для каждого эпизода): Инициализировать s Повторять (для каждого шага эпизода): Найти а по s, используя стратегию, полученную из Q (например, ε-жадную) Выполнить действие а, найти r, s¢
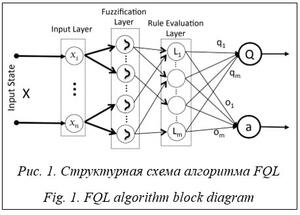
s ¬ s¢ Пока s не станет завершающим состоянием Недостатком данного подхода является необходимость дискретизировать все возможные пары «состояние–действие» и анализировать их многократно для нахождения оптимальных значений функции ценности. Чтобы решить эту проблему, предлагается использовать нечеткую логику для моделирования состояний и функции вознаграждения. Обучение с подкреплением с применением нечеткой логики Нечеткое Q-обучение (fuzzy Q-learning, FQL) – это расширение алгоритма Q-обучения, позволяющее преодолеть упомянутую выше проблему [7]. Кроме того, FQL позволяет инкапсулировать экспертные знания в систему, ускоряя процесс обучения. В FQL принятие решений представлено системой нечеткого логического вывода (fuzzy inference system, FIS), которая рассматривает большие дискретные или непрерывные состояния как входные данные. Идея алгоритма FQL заключается в использовании так называемой q-таблицы в качестве компактной версии Q-таблицы для представления обучающих данных. В FQL система логического вывода описана набором правил J, где j Î J определяется как IF(x1 is Lj1)…AND (xn is Ljn)… AND (xN is LjN) THEN a = oj with q(Lj, oj), где Ljn – метка входной переменной xn, x – вектор состояния, x = [x1, …, xn, …, xN], участвующий в j-правиле; oj = [oj1,…, ojk,…, ojK] – выходное множество действий для правила j, каждому из которых соответствует вектор Lj = [Lj1, …, Ljn,…, LjN]. Значение Q(Lj, ojk) называется значением q-функции в состоянии Lj и действии ojk j-го правила.
Алгоритм FQL имеет двухуровневый выбор действия. На первом уровне (уровень локальных действий) набор действий выбирается в соответствии со стратегией разведки/применения. Такая стратегия позволяет агенту исследовать неопробованные действия, чтобы получить больше опыта, и сочетать это с использованием уже известных успешных действий для обеспечения высокого долгосрочного вознаграждения. В реализации алгоритма используется ε-жадный метод в качестве стратегии для экспериментов. В этом методе на каждом временном шаге агент выбирает случайное действие с фиксированной вероятностью 1 – ε, где ε обычно берется близким к 1. С вероятностью ε действие выбирается жадно из изученных оптимальных действий по отношению к q-таблице с вероятностью
где ojl – выбранное локальное действие j-го правила. На втором уровне выбора действия (выбор предполагаемого действия) назначенное действие для входного вектора x выбирается из набора локальных действий следующим образом:
Чтобы подчеркнуть временную зависимость, в уравнение добавляется индекс времени. Аппроксимация значения качества состояния xt вычисляется на основе уравнения
После выполнения действия a система переходит в следующее состояние xt + 1, агент получает вознаграждение rt + 1. Для входного вектора xt+1 вычисляется значение Value-функции состояния:
Учитывая приведенные выше уравнения, вычисляется TD-ошибка:
где γ – дисконтирующий множитель. Обновление q-функции для каждого активного правила j Î Jx выглядит следующим образом:
Компьютерное моделирование Сравнение эффективности RL-обучения на основе темпоральных различий с применением нечеткой логики проводилось с описанными в [2] методами RL-обучения. С применением ИНС DQN, DDQN и AC (Actor-Critic) были реализованы и испытаны соответствующие алгоритмы глубокого RL-обучения [2, 9, 10]. Для тести- рования методов выбраны хорошо известные задачи, такие как перевернутый маятник (CartPole) и задача о горном автомобиле (Mountain Car).
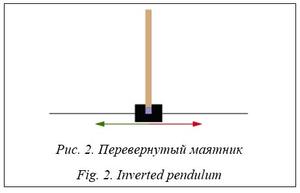
Среда задается состоянием, действием, наградой, начальным состоянием и флагом завершения эпизода. Состояние описывается следующими величинами: - позиция тележки – значение в диапазоне [-4.8, 4.8]; - скорость тележки; - угол отклонения шеста от вертикали – значение в диапазоне [-24°, 24°], (-0.204, 0.204) в радианах; - скорость изменения угла наклона шеста. Действие может принимать значения 0 и 1: 0 – толкнуть тележку влево (приложить к ней горизонтальную силу, равную +1); 1 – толкнуть тележку вправо (приложить к ней горизонтальную силу, равную -1). Награда на каждом шаге равна 1, при падении стержня – награда -1. Начальное состояние задается как [0,0,0,0]. Случаи завершения эпизода: - угол шеста вышел из диапазона [-12°, 12°]; - позиция тележки вышла из допустимого диапазона [-2.4, 2.4]; - длина эпизода >500.
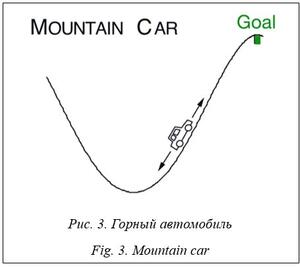
Среда MountainCar описывается рядом компонентов. Состояние среды определяется двумя величинами: - позиция автомобиля: это значение указывает положение автомобиля на горизонтальной оси (диапазон значения – от -1.2 до 0.6); - скорость автомобиля: это скорость движения автомобиля по горизонтальной оси (диапазон значения – от -0.07 до 0.07). Агент может выбирать одно из трех действий: - двигаться влево: автомобиль будет приме- нять газ и двигаться влево; - ничего не делать: автомобиль не изменяет скорость; - двигаться вправо: автомобиль будет при- менять газ и двигаться вправо. Награда: на каждом шаге агент получает награду -1. Цель агента – въехать на вершину горы, по достижении вершины горы агент получает награду 0. Достижение вершины горы считается успешным завершением задачи. Начальное состояние задается следующим образом: позиция автомобиля – случайное значение из интервала [-0.6, -0.4], скорость автомобиля – 0. Случаи завершения эпизода: - достигнута вершина горы – позиция автомобиля >0.5; - длина эпизода >200. Был реализован алгоритм Q-обучения с нечеткой логикой (FQL). Для сравнительного анализа использовались DRL-методы DQN, DDQN и AC, реализованные в [8]. Приведем нечеткие правила для задач CartPole и MountainCar. Нечеткие правила для задачи перевернутого маятника:
Нечеткие правила для задачи горного автомобиля:
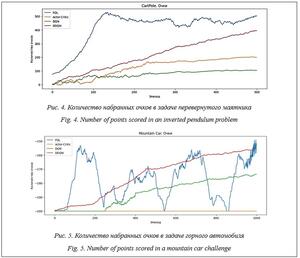
Из графика на рисунке 4 можно сделать вывод, что алгоритм с применением нечеткой ло- гики FQL лучше справляется с задачей перевернутого маятника, чем DRL-методы DQN, DDQN и AC, которые также показывают достаточно высокую эффективность. Нечеткая логика позволила за довольно малое число эпизодов (127) достичь высокой награды в 497 очков (максимально возможная награда 500 очков). На рисунке 5 представлены графики зависимости среднего вознаграждения от номера эпизода в задаче горного автомобиля. Для этой задачи алгоритм FQL за малое число эпизодов (116) достиг награды -155, в то время как алгоритму DDQN потребовалась 1 000 эпизодов для достижения награды -158, а алгоритм AC не справился с задачей. Однако в некоторых эпизодах FQL не смог справиться с задачей (например, при награде -200), что указывает на недостаточное описание системы нечеткими правилами. Изменение набора нечетких правил позволяет улучшить результаты. Реализация алгоритмов выполнена в среде Google Collab с использованием Python 3.10. Заключение В статье рассмотрен метод RL-обучения на основе TD-методов с применением нечеткой логики. Проведен сравнительный анализ алгоритма глубокого обучения с подкреплением с применением нечеткой логики FQL с алгоритмами на основе DRL-методов DQN, DDQN и AC. Проанализированы результаты работы методов обучения с подкреплением с применением нечеткой логики при компьютерных испытаниях реализованных на их основе алгоритмов обучения. Можно отметить основные достоинства алгоритмов обучения с подкреплением с применением нечеткой логики. Эффективность обучения: такие алгоритмы требуют меньшего количества эпизодов, поскольку обобщают знания из небольшого набора обучающих примеров. Это особенно важно, когда доступность данных для обучения ограничена или обучение в реальном времени требует быстрой адаптации. Устойчивость к шуму: алгоритмы устойчивы к шуму и выбросам в данных, поскольку нечеткая логика учитывает их вариации и осуществляет обработку более гибко. Это важно в реальных средах, где существуют шумы или изменения в данных. Интерпретируемость: алгоритмы с нечеткой логикой предоставляют интерпретируемые правила и выводы на основе нечеткой логики. Алгоритм позволяет понять, какие правила и механизмы лежат в основе принятия решений моделью. Кроме того, расширяется область применения Q-обучения: нечеткая логика позволяет использовать его для задач с непрерывным пространством состояний. В настоящее время рассматривается возможность интеграции методов RL-обучения (на основе Q- и TD-методов) с нейронными сетями в плане как использования RL-обучения для формирования обучающей выборки для нейронных сетей глубокого обучения, так и применения нейронных сетей при построении функций активации для Q-обучения. Список литературы 1. Еремеев А.П., Кожухов А.А. Реализация методов обучения с подкреплением на основе темпоральных различий и мультиагентного подхода для интеллектуальных систем реального времени // Программные продукты и системы. 2017. Т. 30. № 1. С. 28–33. doi: 10.15827/0236-235X.117.028-033. 2. Еремеев А.П., Сергеев М.Д. Интеграция методов обучения с подкреплением и искусственных нейронных сетей // Международный научно-технический конгресс ИС & ИТ-2022: тр. конгресса. 2022. С. 10–21. 3. Саттон Р.С., Барто Э.Г. Обучение с подкреплением; [пер. с англ]. М.: ДМК Пресс, 2020. 552 c. 4. Осипов Г.С. Методы искусственного интеллекта. М.: Физматлит, 2011. 296 с. 5. Chen Z., Deng S., Chen X., Li C., Sanchez R.-V., Qin H. Deep neural networks-based rolling bearing fault diagnosis. Microelectronics Reliability, 2017, vol. 75, pp. 327–333. doi: 10.1016/j.microrel.2017.03.006. 6. Hsu C.-C., Lin C.-W. CNN-based joint clustering and representation learning with feature drift compensation for large-scale image data. IEEE Transactions on Multimedia, 2017, vol. 20, no. 2, pp. 421–429. doi: 10.1109/TMM.2017.2745702. 7. Glorennec P.Y., Jouffe L. Fuzzy q-learning. Proc. Int. Fuzzy Systems Conf., 1997, vol. 2, pp. 659–662. doi: 10.1109/FUZZY.1997.622790. 8. Masoumzadeh S.S., Hlavacs H., Tomás L. A self-adaptive performance-aware capacity controller in overbooked datacenters. Proc. ICCAC, 2016, pp. 183–195. doi: 10.1109/ICCAC.2016.8. 9. François-Lavet V., Henderson P., Islam R., Bellemare M.G., Pineau J. An introduction to deep reinforcement learning. Foundations and Trends in Machine Learning, 2018, vol. 11, no. 3-4, pp. 219–354. doi: 10.1561/2200000071. 10. Mnih V., Kavukcuoglu K., Silver D., Rusu A.A., Veness J., Bellemare M.G. et al. Human-level control through deep reinforcement learning. Nature, 2015, vol. 518, no. 7540, pp. 529–533. doi: 10.1038/nature14236. References 1. Eremeev, A.P., Kozhukhov, A.A. (2017) ‘Implementation of reinforcement learning methods based on temporal differences and a multi-agent approach for real-time intelligent systems’, Software & Systems, 30(1), pp. 28–33 (in Russ.). doi: 10.15827/0236-235X.117.028-033. 2. Eremeev, A.P., Sergeev, M.D. (2022) ‘Integration of training methods with reinforcement and artificial neural networks’, Proc. Int. Congress "IS & IT-2022", pp. 10–21 (in Russ.). 3. Sutton, R.S., Barto, A.G. (2018) Reinforcement Learning. MA, Cambridge: The MIT Press, 552 p. (Russ. ed.: Moscow, 2020, 552 p.). 4. Osipov, G.S. (2015) Methods of Artificial Intelligence. Moscow, 296 p (in Russ.). 5. Chen, Z., Deng, S., Chen, X., Li, C., Sanchez, R.-V., Qin, H. (2017) ‘Deep neural networks-based rolling bearing fault diagnosis’, Microelectronics Reliability, 75, pp. 327–333. doi: 10.1016/j.microrel.2017.03.006. 6. Hsu, C.-C., Lin, C.-W. (2017) ‘CNN-based joint clustering and representation learning with feature drift compensation for large-scale image data’, IEEE Transactions on Multimedia, 20 (2), pp. 421–429. doi: 10.1109/TMM.2017.2745702. 7. Glorennec, P.Y., Jouffe, L. (1997) ‘Fuzzy q-learning’, Proc. Int. Fuzzy Systems Conf., 2, pp. 659–662. doi: 10.1109/FUZZY.1997.622790. 8. Masoumzadeh, S.S., Hlavacs, H., Tomás, L. (2016) ‘A self-adaptive performance-aware capacity controller in overbooked datacenters’, Proc. ICCAC, pp. 183–195. doi: 10.1109/ICCAC.2016.8. 9. François-Lavet, V., Henderson, P., Islam, R., Bellemare, M.G., Pineau, J. (2018) ‘An introduction to deep reinforcement learning’, Foundations and Trends in Machine Learning, 11(3-4), pp. 219–354. doi: 10.1561/2200000071. 10. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A.A., Veness, J., Bellemare, M.G. et al. (2015) ‘Human-level control through deep reinforcement learning’, Nature, 518 (7540), pp. 529–533. doi: 10.1038/nature14236. | ||||||||||||||||||||||||
http://swsys.ru/index.php?id=5038&lang=.&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- О реализации средств машинного обучения в интеллектуальных системах реального времени
- Реализация методов обучения с подкреплением на основе темпоральных различий и мультиагентного подхода для интеллектуальных систем реального времени
- Задачи построения интеллектуальной информационной системы управления безопасностью дорожного движения
- Программные средства поддержки принятия решений на основе нечетких табличных моделей представления знаний
- Построение онтологии на основе нереляционной базы данных для интеллектуальной системы поддержки принятия решений медицинского назначения