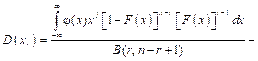Вычисления обратных функций распределений: алгоритмы и программы
| Агамиров Л.В. (mmk@mati.ru) - Национальный исследовательский университет «Московский энергетический институт» (профессор), Москва, Россия, доктор технических наук, Агамиров В.Л. (avl095@mail.ru) - Московский авиационный институт (национальный исследовательский университет) (аналитик), Москва, Россия, кандидат технических наук, Вестяк В.А. (kaf311@mai.ru) - Московский авиационный институт (национальный исследовательский университет) (зав. кафедрой), Москва, Россия, доктор физико-математических наук | |
| Ключевые слова: распределение Вейбулла, нормальное распределение, распределение порядковых статистик, точное распределение коэффициента вариации, нецентральное распределение Стьюдента, javascript, алгоритмы и программы |
|
| Keywords: Weibull distribution, normal distribution, order statistics distribution, variation coefficient exact distribution, non-central Student distribution, javascript, algorithms and programs |
|
|
|
|
Введение. В прикладных задачах математической статистики существует ряд случайных переменных, точный расчет функций распределения которых вызывает значительные вычислительные трудности из-за наличия бесконечных пределов интегрирования, необходимости минимизации целевых функций, отсутствия удовлетворительных аппроксимаций и т.п. К таким распределениям относятся нецентраль- ное распределение Стьюдента, распределения коэффициента вариации, порядковых статистик и другие. Кроме задач вычисления мощности статистических критериев, значения квантилей нецентрального распределения Стью- дента необходимы в задачах надежности для обоснования толерантных интервалов и гарантированных ресурсных характеристик техни- ческих систем [1]. Область применения коэффициента вариации в инженерных задачах рассматривается в работах [1, 2]. Доказательство точного распределения коэфффициента вариации для нормальной выборки содержится в классической книге Лемана [3], все последующие работы – это различной точности аппроксимации этого распределения. Математические ожидания и ковариации порядковых статистик широко применяются в прикладных задачах математической статистики. Анализ литературных источников по теме данного исследования, связанного с разработкой алгоритмов и программ для точного вычисления функций статистических распределений, показал, что их количество весьма ограниченно. Так, например, в [4, 5] рассматривается наиболее распространенное применение обратных функций – моделирование случайных величин методом обратных функций, а также разработка аналитических приближений для обращения функций вероятностных распределений [6]. Многие исследования посвящены новым методам представления аналитических аппроксимаций для прямых и обратных функций сложных нецентральных статистических распределений [7–9]. В то же время непосредственно связанные с темой данной работы источники практически отсутствуют. По мнению авторов, причина в том, что в настоящее время специалисты в области прикладной статистики используют в основном аппроксимации, созданные в математических пакетах с закрытым ко- дом типа Boost [10], Matlab, Statistica, Mathcad и в других. В свою очередь, как показал анализ документации по этим пакетам, они в значительной степени основаны на алгоритмах и программах прикладной статистики в рамках проекта Royal Statistical Society “Applied Statistics algorithms” (http://lib.stat.cmu.edu/apstat/), содержащего около 250 алгоритмов начиная с 1968 г. (проект завершился в 1997 г.), переведенных с языка Algol на Fortran, а затем на С++ (https://people.sc.fsu.edu/~jburkardt/cpp_ src/cpp_ src.html). Точные вычисления содержатся в уникальных статистических таблицах [11] и их русскоязычных аналогах (особенно в части нецентральных распределений) [12], которые, возможно, выполнены методами численного интегрирования в специализированных математических институтах, но недоступны для анализа кода и использования в задачах компьютерного моделирования. Кроме того, приведенные в табличном виде процентные точки обладают дискретностью, что вызывает необходимость интерполяции или экстраполяции, а это, в свою очередь, снижает точность расчетов. Очевидно, что при современном уровне развития информационных технологий использование таблиц является анахронизмом и может служить лишь для контроля точности численных расчетов, а также в учебных целях. Следует также упомянуть статистические программы, встроенные в популярный язык Python, которые полностью базируются на динамических библиотеках Boost с закрытым кодом. В отличие от Python эти библиотеки в стандарт C++ пока не встроены и требуют отдельной, часто трудоемкой установки. Тем не менее анализ некоторых открытых кодов статистических функций Boost показывает, что они основаны на многоуровневых аппроксима- циях, выполненных многими исследователями в разное время с множеством условий. Преимуществами аппроксимаций Boost являются их высокая точность и практически мгновенное действие. Аппроксимации, встроенные в специализированный язык R (The R Project for Statistical Computing, https://www.r-project.org), уступают по точности функциям Boost. Все сказанное касается, разумеется, сложных распределений, стандартные распределения в данной работе не рассматриваются. Таким образом, исследования, направленные на разработку ПО для реализации точных алгоритмов вычисления сложных функций статистических распределений, являются актуальной задачей. При этом точность решений определяется точностью не аппроксимаций, а численного интегрирования и методов минимизации, которые можно неограниченно увеличивать с учетом лишь временных затрат. Следует также отметить, что приемлемых по точности расчетов параметров порядковых статистик авторы не обнаружили, поэтому преимуществом предлагаемых методов расчета прямым интегрированием сложных функций с последующей минимизацией целевых функций является не только точность вычислений (зачастую аппроксимации дают не меньшую точность), но и сам подход. Он позволяет распространять данную методику практически на любую схожую задачу с небольшими ограничениями типа непрерывности и дифференцируемости исходных функций, в то время как аппроксимацию следует полностью модифицировать для каждой конкретной задачи с тщательным последующим тестированием. Исключения, разумеется, встречаются, например, при численном интегрировании двойных интегралов с бесконечными пределами. В этих случаях альтернативы аппроксимациям нет из-за неоправданно больших временных затрат. Целью настоящего исследования является разработка алгоритмов и программ расчета обратных функций сложных статистических распределений. Описываемые алгоритмы пригодны для широкого класса непрерывных распределений. В рассматриваемых программах применяются лишь простейшие и достаточно точные аппроксимации стандартных распределений. В настоящей работе это аппроксимации нормального распределения, гамма-функции, неполной гамма-функции, точность которых оказалась выше алгоритмов на Фортране (библиотека SSP) [13]. Авторы предлагают алгоритмы и программы на языке Javascript [14], ко- торые выложены по адресу http://g2.plzvpn.ru: 3000/Rank/rank.html (исходный програм- мный код реализации по ссылке https://github. com/AVL095/Inverse_distribution_functions). Выбор языка обусловлен его общедоступностью и быстродействием. Вышеуказанные задачи основаны на распределении отношения независимых случайных величин x = z1/z2:
или
где f1(t), F1(t) – функция плотности и функция распределения случайной величины z1; f2(t), F2(t) – функция плотности и функция распределения случайной величины z2. В соответствии с этим в выборке объема n из нормального распределения N(a, s) с выборочными средним
откуда определяется квантиль распределения уровня b. Здесь
функция распределения нормального закона; d – параметр нецентральности; f = n – 1 – число степеней свободы. Распределение выборочного среднего подчиняется нормальному закону с параметрами N(a, d/n0.5). Переменная y = s2(n – 1)/d2 имеет c2 распределение с f степенями свободы и плотностью
где Г(x) – гамма-функция (см. модуль stat.js). Плотность выборочного распределения стандартного отклонения x = (s2/f)0.5 в формуле (3) определяется на основании теоремы о плотности монотонной функции случайной величины:
Таким образом, распределение коэффициента вариации g = s/a подчиняется нецентраль- ному распределению Стьюдента с параметром нецентральности d = (n)0.5/g и числом степеней свободы f [3], то есть Поэтому для вычисления квантилей коэффициента вариации достаточно иметь квантили нецентрального распределения Стьюдента. Прямое вычисление функции распределения выборочного коэффициента вариации сводится к уравнению
откуда определяется квантиль распределения коэффициента вариации уровня b, g – генеральное значение коэффициента вариации. В настоящей работе анализировались оба подхода, по точности и быстродействию они показали идентичные результаты. Для вычисления функций нецентрального распределения Стьюдента и коэффициента вариации необходимо численное интегрирование уравнений (3) или (6). Квантили распределения, соответствующие заданной вероятности, определялись последовательными приближениями. С этой целью в настоящей работе использовался симплекс-метод Нелдера–Мида (деформируемого многогранника). Алгоритм расчета обратной функции нецентрального распределения Стьюдента реализован путем интегрирования уравнения (3) с последующей минимизацией квадратичной функции q = (b – b0)2, представляющей собой квадрат разности заданной b0 и расчетной b доверительных вероятностей. Параметры функции simpl (модуль stat.js): x[nx] – вектор размерности nx, на входе содержащий начальные приближения, на выходе – точки минимума; nx – число переменных минимизируемой функции (в рассматриваемом случае nx = 1); step – начальный шаг минимизации; eps – относительная точность выхода; lim – максимальное число итераций, функция simpl возвращает число выполненных итераций iter; funx – имя минимизируемой функции. Вызов функции: iter = simpl(x, nx, stepx, eps, lim, funx). Численное интегрирование уравнения (3) осуществлялось методом Буля (модуль stat.js). Параметры функции IntegrateFunction: k – номер выбранного метода, соответствующий размерности аппроксимирующего полинома (3, 4 – метод Симпсона, 5 – метод Буля); nstep – количество шагов интегрирования; xl, xu – нижний и верхний пределы интегрирования; fpolinom – имя интегрируемой функции, функция возвращает значение интеграла. Вызов функции: beta = = IntegrateFunction(k, nstep, xl, xu, fpolinom). Вспомогательные программы содержатся в модуле stat.js. С целью исключения возможных ошибок в программах используются лишь простейшие и проверенные конструкции языка Javascript, включая ввод данных и вывод результатов на экран. Аналогичный алгоритм реализован и для распределения коэффициента вариации, он отличается только типом интегрируемой функции (в данном случае (6)). Как показали расчеты, быстрый и успешный поиск точек минимума в программе simpl существенно зависит от заданных на входе начальных приближений. С этой целью использовалась следующая нормальная аппроксимация квантиля [1] (функция invnontap в модуле stat.js):
где d – параметр нецентральности; f – число степеней свободы; zb – квантиль нормированного нормального распределения уровня b; b – доверительная вероятность. Применительно к распределению коэффициента вариации в качестве первого приближения использовалась аппроксимация
где np – квантиль распределения коэффициента вариации уровня вероятности p; g – генеральное значение коэффициента вариации; c2p, f – квантиль распределения хи-квадрат [1]. Аппроксимация (8) дает существенные погрешности при значениях g, больших 0,3. Менее сложной с точки зрения программирования представляется задача точного вычисления числовых характеристик (математических ожиданий E(xr) и дисперсий D(xr)) порядковых статистик xr [2, 4, 5] в выборке объема n прямым интегрированием:
где r = 1 – n – номер порядковой статистики; j(x) – плотность распределения; F(x) – функция распределения; B(a, b) – бета-функция. Численное интегрирование осуществляется с помощью функции dataorder в модуле cvar.js. В таблице 1 показаны результаты вычисления квантилей нецентрального распределения Стьюдента. В программе варьировались объем испытаний n от 3 до 50, вероятности p от 0,01 до 0,99 и доверительные вероятности 0,9, 0,95 и 0,99. В таблице представлен фрагмент расчетов для n, равных от 3 до 10. Время расчета в полном диапазоне всех параметров составляет не более 10–15 секунд на компьютере невысокой производительности (индекс производительности – 1,0, ОЗУ – 4Гб, процессор – Intel® Pentium® 1,9 GHz). Точность расчета – порядка 10-5. Сопоставления по быстродействию с аналогичными расчетами, выполняемыми приближенными методами, например, в библиотеках Boost, не анализируются, так как вычисления аппроксимаций составляют доли секунды. Необходимо отметить, что изменение требуемой точности расчетов (eps), то есть относительной точности выхода в программе минимизации, практически не влияет на машинное время, поскольку при надлежащем задании начальных приближений программа очень быстро выходит на минимум. В результате вариация этого параметра в широком диапазоне значений приводит к одним и тем же точечным оценкам с незначительным увеличением числа итераций. Несколько большее значение имеют задаваемые предельное число итераций (lim) и шаг минимизации (step), но только тогда, когда программа вообще не находит минимума, что считается неудовлетворительным и подлежит исключению. В этом случае необходимо уточнить начальные приближения. Применительно к задачам, рассматриваемым в данной работе, такого не наблюдалось. Следует также отметить, что скорость вычислений на языке C++ в десятки раз выше, чем на Javascript и Python. Основные временные затраты приходятся именно на численное интегрирование, а программа минимизации работает достаточно быстро (не более 20–30 итераций), что вполне объяснимо, так как в связи с наличием бесконечных пределов интегрирования для достижения требуемой точности необходимо охватить максимальный диапазон переменной независимо от применяемого метода. В рассматриваемых программах верхний предел интегрирования задавался равным 5, но может изменяться пользователем в зависимости от требуемой точности расчетов. В таблице 2 представлены результаты вычислений квантилей относительных коэффициентов вариации np/g для объемов выборки n = 3–10, генеральных коэффициентов вариации g = 0,05, 0,3 и 0,5 и вероятностей p в диапазоне от 0,01 до 0,99. Быстродействие и точность примерно эквивалентны приведенным в предыдущем примере.
Сравнение результатов расчета математических ожиданий и дисперсий нормальных порядковых статистик, полученных аппроксима- цией Дэйвида–Джонсона (функция ordern, модуль stat.js), с порядком разложения в ряд (n + 2)-3 с табличными значениями показывают расхождения лишь в 4-м, 5-м знаке после запятой. В функции ordern содержатся производные функции распределения вплоть до 6-й, а также комментарии. Быстродействие настолько высокое, что в данной работе не анализируется. Предлагаемое авторами прямое интегрирование функций распределения позволяет вычислять также числовые характеристики порядковых статистик для законов распределения, отличных от нормального. Функция распределения Вейбулла, например, с параметрами b и c имеет следующий вид:
Приводя распределение к виду с параметрами сдвига aw = lnc и масштаба sw = 1/b, z = (lnx-aw)/sw, получим соотношения для функции и плотности распределения:
которые подставляются в (9) и (10). Сравнительные расчеты числовых характеристик по- рядковых статистик распределения Вейбулла по интегралам (9), (10) (функция dataorder в модуле cvar.js) и приближенных, основанных на аппроксимации Дэйвида–Джонсона (функция orderw, модуль stat.js), показали расхождения в 3-м, 4-м знаке после запятой. Пользовате- лям рекомендуется самостоятельно принимать решение о применении той или иной модели в зависимости от требуемой точности расчетов. Предлагаемая аппроксимация позволяет также вычислять ковариации порядковых статистик. Точное решение для ковариаций здесь не рассматривается, так как требует вычисления двой- ных интегралов. Поскольку распределение Вейбулла является несимметричным, следуетвычислять все порядковые статистики от 1 до n в отличие от нормального закона. Заключение Разработанные алгоритмы и программы вычисления обратных функций нецентрального распределения Стьюдента и распределения коэффициента вариации основаны на сочетании численного интегрирования и симплекс-метода минимизации, позволяющих получать быстрые и точные решения для применения данных функций в задачах прикладной статистики. Приведенные в таблицах сравнительные расчеты показали высокую точность вычисле- ний и особенности существующих аппроксимаций. Так, например, алгоритмы аппроксимации функции нецентрального распределения Стьюдента дают весьма точные приближения во всем диапазоне вероятностей, объемов выборки и параметров нецентральности и вполне пригодны для последующей минимизации с целью получения процентных точек. В то же время известная аппроксимация McKay для коэффициента вариации дает погрешности до 15 % при значениях коэффициента вариации, больших 0,3. Представленные в полном объеме и в открытом доступе модифицированные программы и аппроксимации на языке Javascript позволяют без труда распространять полученные решения для других статистических задач, связанных с точным распределением отношений двух независимых случайных переменных. Разработанные программы интегрирования функций с бесконечными пределами для получения числовых характеристик порядковых статистик позволяют производить необходимые вычисления для большого класса непрерывных функций распределения. В работе рассмотрены нормированные нормальное и Вейбулла распределения, а также представлены аппроксимации методом Дэйвида–Джонсона. Расчеты показали достаточно высокую точность разложения по сравнению с интегральными решениями (расхождения наблюдаются в 3-м, 4-м знаке после запятой). Список литературы 1. Агамиров Л.В., Вестяк ВА. Вероятностные методы расчета показателей надежности авиационных конструкций при переменных нагрузках. М.: МАИ, 2022. 256 с. 2. Tothfalusi L., Endrenyi L. An exact procedure for the evaluation of reference-scaled average bioequivalence. AAPS J., 2016, vol. 18, no. 2, pp. 476–489. doi: 10.1208/s12248-016-9873-6. 3. Lehmann E.L. Testing Statistical Hypothesis. NY, John Wiley & Sons Publ., 1986, 388 p. 4. Холкина A.B. Моделирование случайных величин методом обратных функций // Математическое и программное обеспечение информационных, технических и экономических систем: матер. VII Междунар. молодежн. научн. конф. 2019. С. 73–75. 5. Царев А.Д. Программные генераторы случайных блужданий // Вестн. КРАУНЦ. Физ.-мат. науки. 2020. Т. 31. № 2. C. 226–235. doi: 10.26117/2079-6641-2020-31-2-226-235. 6. Попов Г.А. Формула обращения для рациональных характеристических функций вероятностных распределений // Вестн. АГТУ. 2018. Т. 2018. № 2. doi: 10.24143/1812-9498-2018-2-7-22. 7. Gil A., Segura J., Temme N.M. New asymptotic representations of the noncentral t-distribution. Studies in Applied Math., 2023, vol. 151, no. 3, pp. 857–882. doi: 10.1111/sapm.12609. 8. Gil A., Segura J., Temme N.M. On the computation and inversion of the cumulative noncentral beta distribution. Appl. Math. Comput., 2019, vol. 361, pp. 74–86. 9. Gil A., Segura J., Temme N.M. A new asymptotic representation and inversion method for the Student’s t distribution. Integral Transforms and Special Functions, 2022, vol. 33, no. 8, pp. 597–608. doi: 10.1080/10652469.2021. 2007906. 10. Полухин А. Разработка приложений на С++ с использованием Boost. М.: ДМК Пресс, 2020. 346 с. 11. Pearson E.S., Hartley H.O. Biometrika Tables for Statisticians. Cambridge University Press, 1976, 286 p. 12. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.: Наука, 1983. 416 с. 13. 1130 Sci. Subroutine Package. Programmer's Manual, Program Number 1130-CM-02X. IBM Corporation, 1967, 191 p. 14. Агамиров Л.В., Вестяк В.А. Программа вычисления обратных функций сложных статистических распределений: Свид. о регистр. ПрЭВМ № 2022612358. Рос. Федерация, 2022. References 1. Agamirov, L.V., Vestyak, V.A. (2023) Probabilistic Methods for Calculating Reliability Indicators of Aircraft Structures under Variable Loads. Moscow, 256 p. (in Russ.). 2. Tothfalusi, L., Endrenyi, L. (2016) ‘An exact procedure for the evaluation of reference-scaled average bioequivalence’, AAPS J., 18(2), pp. 476–489. doi: 10.1208/s12248-016-9873-6. 3. Lehmann, E.L. (1986) Testing Statistical Hypothesis. NY: John Wiley & Sons Publ., 388 p. 4. Kholkina, A.V. (2019) ‘Modeling random variables using the inverse function method’, Proc. VII Int. Youth Sci. Conf. Mathematical Support and Software for Information, Technical and Economic Systems, pp. 73–75 (in Russ.). 5. Tsarev, A.D. (2020) ‘Random walk software generation’, Bull. KRASEC. Phys. and Math. Sci., 31(2), pp. 226–235 (in Russ.). doi: 10.26117/2079-6641-2020-31-2-226-235. 6. Popov, G.A. (2018) ‘Formula of inversion for rational characteristic functions of probability distributions’, Bull. of ASTU, 2018(2), pp. 226–235 (in Russ.). doi: 10.26117/2079-6641-2020-31-2-226-235. 7. Gil, A., Segura, J., Temme, N.M. (2023) ‘New asymptotic representations of the noncentral t-distribution’, Studies in Applied Math., 151(3), pp. 857–882. doi: 10.1111/sapm.12609. 8. Gil, A., Segura, J., Temme, N.M. (2019) ‘On the computation and inversion of the cumulative noncentral beta distribution’, Appl. Math. Comput., 361, pp. 74–86. 9. Gil, A., Segura, J., Temme, N.M. (2022) ‘A new asymptotic representation and inversion method for the Student’s t distribution’, Integral Transforms and Special Functions, 33(8), pp. 597–608. doi: 10.1080/10652469.2021.2007906. 10. Polukhin, A. (2020) Development of Applications in C++ Using Boost. Moscow, 346 p. (in Russ.). 11. Pearson, E.S., Hartley, H.O. (1976) Biometrika Tables for Statisticians. Cambridge University Press, 286 p. 12. Bolshev, L.N., Smirnov, N.V. (1983) Tables of Mathematical Statistics. Moscow, 416 p. (in Russ.). 13. 1130 Sci. Subroutine Package. Programmer's Manual, Program Number 1130-CM-02X (1967) IBM Corporation, 191 p. 14. Agamirov, L.V., Vestyak, V.A. (2022) A Program for Calculating Inverse Functions of Complex Statistical Distributions. Pat. RF, № 2022612358. |
http://swsys.ru/index.php?id=5070&lang=.docs&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:

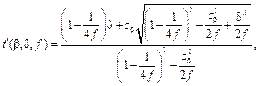 (7)
(7)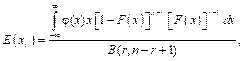 (9)
(9)