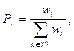Глобальная оптимизация на основе гибридизации алгоритмов роя саранчи и колонии пауков
| Родзин С.И. (srodzin@sfedu.ru) - Южный федеральный университет (доцент, профессор), Таганрог, Россия, кандидат технических наук | |
| Ключевые слова: критерий Уилкоксона, глобальный оптимум, агент, рой саранчи, колония пауков, паттерн поведения, интенсификация поиска, диверсификация поиска, тестовая функция, алгоритм |
|
| Keywords: Wilcoxon test, global optimum, agent, locust swarm, spider colony, behavior pattern, search intensification, search diversification, test function, algorithm |
|
|
|
|
Введение. Эвристические алгоритмы, инспирированные природой, вместе с нейронными сетями и другими методами образуют класс алгоритмов машинного обучения. Для них характерны исследование пространства решений, поиск точек в области определения функции, на которых она достигает минимального или максимального значения, их оценка и селективный отбор. Алгоритм обучается нахож- дению областей определения функции, которые содержат наилучшие решения. Поиск по БД Web of Science, Scopus, Google Scholar, цифровой библиотеке IEEE Xplore, российским библиотекам eLibrary.Ru и «КиберЛенинка» позволяет говорить о существовании более 400 алгоритмов, инспирированных природой [1]. Их число и показатели цитируемости растут: 85 % статей, в которых предлагаются алгоритмы, инспирированные природой, цитируются в среднем около 20 раз, в то время как среднегодовая норма цитирования статей в целом в области Artificial Intelligence составляет около 5 [2]. С 2010 г. по настоящее время лидерами по количеству публикаций являются роевые алгоритмы. Они применяются практически во всех областях науки, техники и экономики. В этих областях многие задачи оптимизации и проектирования нелинейные, зачастую NP-трудные. Между тем такие алгоритмы, как оптимизация роя частиц (PSO), дифференциальная эволюция (DE), колония муравьев (ACO), пчел (ABC), светлячков (FA), поиска кукушки (CS) и многие другие продемонстрировали большой потенциал при решении сложных задач поисковой оптимизации за разумное время [3]. Чтобы алгоритм, инспирированный природой, был эффективным, он должен обладать некоторыми особыми возможностями. Например, генерировать новые решения, улучшающие существующие путем интенсивного ис- следования локального пространства вокруг найденного текущего хорошего решения (интенсификация). С другой стороны, алгоритм должен быть способным избегать преждевременной сходимости в локальном оптимуме путем расширения области поиска решений и обнаруживать области поиска, где может находиться глобальный оптимум (диверсификация). Удачная комбинация интенсификации и диверсификации поиска способствует высокой эффективности метаэвристики. Поиск баланса этих двух важных компонент любого алгоритма, инспирированного природой, является открытой исследовательской проблемой. Каждая биоэвристика использует различный баланс между ними, зачастую далекий от оптимального. В данной работе предлагается гибридный алгоритм глобальной оптимизации, основанный на модифицированных алгоритмах роя саранчи и колонии пауков, а также исследуется его эффективность на ряде известных тестовых задач. Модифицированный алгоритм роя саранчи Инспирированные природой алгоритмы, описывающие коллективные разумные паттерны поведения в мире животных и насекомых, привлекают внимание исследователей с конца прошлого века. Стереотипные поведенческие паттерны, наблюдаемые в группах животных и скоплениях насекомых, дают преимущества для выживания. Группа особей может решать достаточно сложные задачи, хотя отдельные особи, составляющие группу, относительно просты, используют ограниченную локальную информацию, допускают специализацию задач. Саранча, являясь своего рода крупным кузнечиком, представляет пример таких групп насекомых. Саранча демонстрирует как одиночный, так и роевой паттерны поведения с их четкими поведенческими различиями [4]. При одиночном поведении, когда много пищи и места, саранча избегает контакта, поэтому рой исследует пространство, распределившись по всей площади. Паттерн роевого поведения, наоборот, означает стремление саранчи к агрегации вокруг перспективных источников пищи [5]. Использование в алгоритме оптимизации тако- го рода специализированных паттернов поведения позволяет поддерживать необходимый баланс между интенсификацией и диверсифи- кацией поиска, избегать преждевременной сходимости к неоптимальным решениям. В алгоритме это достигается путем включения операторов, моделирующих роевые и одиночные паттерны поведения агентов популяции. Речь идет о тех, кто отвечает за изменение позиций особей роя саранчи на текущей итерации алгоритма. В природе налетевший рой саранчи, механизм образования которого достаточно сложен, способен уничтожить огромную площадь посевов за несколько часов. В работе [6] представлен алгоритм оптимизации, моделирующий поиск пищи роем саранчи, а в [5] – биологическая модель одиночного и роевого поведения саранчи, которая применяется при разработке модифицированного алгоритма роя саранчи. Рассмотрим паттерн одиночного поведения особи саранчи и связанное с ним изменение ее позиции. Обозначим через xik позицию i-й осо- би в рое из N особей на k-м шаге алгоритма. Позиция i-й особи на следующем шаге алгоритма xik+1 определяется как xik+1 = xik + D xi, где величина Dxi отражает изменение позиции i-й саранчи. Паттерн одиночного поведения предполагает, что пара особей избегает сближения при условии короткой дистанции между ними. Если же дистанция между особями велика, то они начинают сближаться, поддерживая сплоченность роя. Следуя [7], определим силу сближения/удаления саранчи следующим образом: s(r) = kar e–r/lim – e–r, (1) где r – дистанция между парой особей; kar – коэффициент сближения/удаления; lim – пороговая дистанция между особями. Сила удаления превышает силу сближения, если kar < 1 и lim > 1, то есть дистанция между особями небольшая. Иными словами, сила взаимодействия между парой особей зависит от дистанции между ними: sij = s(rij)dij, где rij = |xj – xi| – дистанция между i-й и j-й особями роя; dij = (xj – xi)/rij – единичный вектор. Тогда сумма всех сил взаимодействия с роем для i-й особи дает общую силу сближения/удаления роя и определяет изменение позиции i-й саранчи:
Триггером перехода от одиночного поведения саранчи к роевому являются изменения в окружающей среде. Рой в поисках пищи ведет себя очень сплоченно. Характерная черта паттерна роевого поведения заключается в стремлении роя сконцентрироваться вблизи особей, которым удалось найти пищу. Эту особенность роевого поведения можно смоделировать путем введения для каждой особи роя саранчи индикатора пищи fi (fi Î [0, 1]). После сортировки N особей роя производится отбор b доминирующих особей (b << N) с наибольшим значением индикатора fi, вблизи которых концентрируются остальные особи. Рой саранчи из N особей образует популяцию решений Lk({l1k, l2k, ..., lN k}) оптимизационной задачи, где число итераций k = 0, 1, 2, ..., gen. Особь саранчи lik (i = 1..N) характеризуется через множество {li1k, li2k, ..., link}. Элемент этого множества отображает отдельную переменную оптимизационной задачи. Ограничения в задаче образуют множество допустимых решений: S = {lik Î Rn |lbd ≤ lid k ≤ ubd}, где lbd - нижняя граница размерности d; ubd - верхняя граница размерности d. Фитнесс-функция fi(lik) характеризует уровень индикатора пищи каждой саранчи. Таким образом, модифицированный алгоритм роя саранчи (МАРС) использует оператор Оод, характеризующий паттерн одиночного поведения саранчи, и Орой, характери- зующий паттерн роевого поведения саранчи. Оператор Оод способствует диверсификации области поиска решений и обнаружению точки глобального оптимума, а оператор Орой – интенсивному исследованию локального пространства вокруг найденного текущего хорошего решения. С помощью оператора Оод позиция lik i-й особи изменяется на величину Dlik и становится равной pi = lik + Dlik. При этом учитывается позиция доминирующих особей роя с наибольшим значением фитнесс-функции. Тогда сила сближения/удаления между парой особей (i, j) вычисляется следующим образом: sijm = ρ(lik, ljk) s(rij)dij + rand(1, –1), где s(rij) вычисляется согласно (1); dij направлен от lik к ljk; функция rand(–1, 1) генерирует случайное число из интервала (–1, 1); функция ρ(lik, ljk) указывает на доминирование между парой особей (i, j). Особи с наибольшим значением фитнесс-функции присваивается ранг 0, а с наименьшим - ранг N–1. Функция доминирования ρ определяется следующим образом:
где функция rank(α) указывает на ранг особи. Согласно (3), функция ρ принимает значения из интервала (0, 1). Значение ρ = 1 в случае, если особь имеет наилучшее значение фитнесс-функции в популяции. Значение ρ, близкое к 0, свидетельствует о низком значении фитнесс-функции. После обновления множества позиций {p1, p2, …, pN} особей колонии Lk корректируются значения множества фитнесс-функций F(f1, f2, …, fN). Причем результаты поиска должны улучшаться: если fi (pi) > fi(lik), то особь перемещается в новую позицию pi, в противном случае позиция lik остается неизменной. С помощью оператора Орой производится интенсивное исследование локального пространства вокруг найденного текущего хорошего решения. Это происходит путем упорядочения фитнесс-функций особей по убыванию. Затем результаты упорядочения запоминаются в массиве B = {b1, b2, …, bN}. Из массива B выбираются g особей с наилучшими значениями фитнесс-функции, которые составляют множество E наиболее перспективных для дальнейшего исследования решений. Исследование производится в окрестности каждой i-й особи из множества E. Радиус окрестности вычисляется по формуле
где ubq и lbq – верхняя и нижняя границы в q-м измерении соответственно; n – размерность переменных в задаче оптимизации; b Î [0, 1] – параметр алгоритма. Верхняя граница ussqj и нижняя граница lssqj окрестности Cj в q-м измерении вычисляются по следующим формулам: ussjq = bj,q + ed, lssjq = bj,q – ed. В окрестности Cj создаются h (h < 4) новых особей. Победителем является особь с наилучшим значением фитнесс-функции. Таким образом, управляющими параметрами алгоритма МАРС являются kar – коэффи- циент сближения/удаления, lim – пороговая дистанция между особями, g – число особей с наилучшими фитнесс-функциями, N – размер популяции и gen – число поколений. В процессе инициализации алгоритма МАРС устанавливается начальное значение счетчика поколений (k = 0) и случайно генерируется начальная популяция L0({l10, l20, ..., lN0}). При этом для измерения d предварительно задаются верхняя начальная граница параметра (ubd) и нижняя начальная граница параметра (lbd), в которых значения ({li10, li20, ..., lin0}) распределены случайно и равномерно: lij0 = lbd + rand(ubd – lbd), где i = 1..N, d = 1..n. Далее в алгоритме выполняются операторы Оод, характеризующий паттерн одиночного поведения саранчи, и Орой, характеризующий паттерн роевого поведения саранчи для поддерж- ки баланса интенсификации/диверсификации. Останов алгоритма происходит при достижении числа итераций k = gen. Представим псевдокод МАРС: 1: Ввод: kar, lim, g, N, gen 2: Инициализация L0 (k = 0) 3: until (k = gen) 4: F ¬ оператор Оод (Lk) 5: Lk+1 ¬ оператор Орой (Lk, F) 6: k = k + 1 7: end until Модифицированный алгоритм колонии пауков В работе [8] представлен алгоритм оптимизации, моделирующий кооперативное поведение колонии социальных пауков, а в [9] – биологическая модель их взаимодействия. Используем эту модель для представления паттернов поведения в распределенной самоорганизующейся сети и построения модифицированного алгоритма колонии пауков (МАКП). Основными функциями, характеризующими поведение пауков в колонии, являются строительство сетевой паутины, размножение и охота. При этом инструментом взаимодействия агрегации пауков является сеть. Она представляет собой канал связи через вибрации и постукивания. Вибрации используются пауками для синхронизации и декодирования своих действий, а также для авторизации особи, передающей сообщение. По интенсивности вибраций и постукиваний определяются вес паука и расстояние до него. Каждый шаг паука вызывает вибрацию. Поэтому, например, при охоте коло- ния перестает двигаться, чтобы по сети почувствовать добычу и понять правильное направление движения. Колония использует опре- деленную тактику и командную работу для защиты своих ресурсов и потомства с дифференциацией ролей. Согласно биологической модели определим паттерны поведения пауков – размножение и кооперация [10]. Альфа-самцы пауков отличаются большим весом в сравнении с остальными самцами. При размножении они стремятся двигаться по сети к ближайшей самке. В отличие от альфа-самцов недоминирующие самцы в основном сосредоточиваются в центре колонии, чтобы воспользоваться ресурсами альфа-самцов. С учетом этого МАКП включает следующую последовательность шагов. Шаг 1. Инициализация популяции пауков S = B È M размером N. Поскольку, согласно биологической модели, в колонии преобладают самки, то их число Nb определяется по формуле Nb = floor [(0,9 – rand0,25)N], где rand – случайное число в интервале [0, 1]; floor(·) – функция преобразования действительных чисел в целые. Общее число самцов Nm = N – Nb. В целом колония социальных пауков S размером N состоит из подмножеств B = {b1, b2, …, bNb} и M = {m1, m2, …, mNm}. Шаг 2. Случайная инициализация позиций пауков. Позиции самцов bi и самок mj генерируются случайно и равномерно. Для этого задаются нижний начальный параметр qkниж и верхний начальный параметр qkверх : bi,k0 = qkниж + rand(0,1)(qkверх – qkниж), mj,k0 = qkниж + rand(0,1)(qkверх – qkниж), где i = 1…Nb, j = 1...Nm, k = 1...n; функция rand(0, 1) генерирует случайное число в интервале от 0 до 1. Шаг 3. Диапазон взаимодействия в колонии социальных пауков определяется размерами пространства поиска по формуле
Шаг 4. Вероятность участия в процессе размножения зависит от веса паука и вычисляется по методу рулетки:
где Tg – множество пауков в радиусе r. При этом сохраняется первоначальная пропорция между самками и самцами в популяции S. Шаг 5. Позиция самки bi на итерации алгоритма (t + 1) изменяется по формулам: bit+1 = bit + aVibi,u(mu – bit) + bVibi,maxw(mmaxw – – bit) + d(rand – 1/2) с вероятностью PF, bit+1 = bit + aVibi,u(mu – bit) + bVibi,maxw(mmaxw – – bit) + d(rand – 1/2) с вероятностью 1 – PF. Здесь моделируются вибрации паутины. Вибрации зависят от веса и расстояния до паука, который их породил. Иными словами, особи рядом с пауком, создающим вибрации, улавливают их как более сильные, нежели осо- би, находящиеся вдали. Вибрация, которую 𝑖-й паук улавливает от 𝑗-го паука, определяется как Vibi, j = wj где di, j = ‖ si – sj ‖ – евклидово расстояние между i-м и j-м пауками. Модификация алгоритма заключается в использовании в МАКП следующих вариантов вибраций: ● Vibci = wc ● Vibbi,maxw = wmaxw ● Vibfi = wf Шаг 6. Выполняется оператор, моделирующий движение самца паука:
где sb – ближайшая к пауку самка, а величина Оператор определяет различные поведенческие паттерны, что способствует диверсификации поиска оптимума. К тому же уменьшается влияние очень хороших и плохих решений на результаты поиска. Шаг 7. Выполняется оператор размножения в определенном диапазоне r, который вычисляется как
где Tg – множество пауков в радиусе r, которые участвуют в размножении. Шаг 8. Останов алгоритма происходит при достижении заданного максимального числа итераций. Иначе – возврат к шагу 4 алгоритма. Гибридизация алгоритмов МАРС и МАКП Комбинирование нескольких алгоритмов, инспирированных природой, при решении целого класса сложных задач глобальной оптимизации может оказаться более эффективным, нежели использование одного алгоритма. Перспективным направлением здесь является гибридизация различных алгоритмов глобальной оптимизации. Существуют различные способы гибридизации алгоритмов. Одним из них является последовательная комбинация алгоритмов (препроцессор/постпроцессор). Основная идея этого способа гибридизации заключается в том, чтобы на начальных этапах обеспечить широкий обзор всевозможных решений, а на последующих сузить области поиска. Сценарий предлагаемой гибридизации вклю- чает поиск решений с помощью алгоритма МАКП в качестве препроцессора, а затем проверку и выявление лучшего решения с помощью алгоритма МАРС. Триггером перехода с алгоритма препроцессора является отсутствие улучшения глобального оптимума. Алгоритм постпроцессора стартует, используя в основном решения, полученные на заключительном шаге алгоритма препроцессора с исключением решений, близких к области одного и того же экстремума. Результаты экспериментальных исследований эффективности гибридного алгоритма Для оценки эффективности предлагаемого гибридного алгоритма глобальной оптимизации, основанного на МАКП и МАРС, были проведены эксперименты с использованием тестовых многомерных функций. Эксперименты проводились в программной среде на языке программирования C# с использованием среды программирования приложе- ний Microsoft Visual Studio. Это позволило воспользоваться возможностями, предоставляемыми объектно-ориентированным подходом в разработке ПО, а также максимально использовать фреймворк Windows Forms (зарегистрирована программа для ЭВМ, запись № 2023681642 от 17.10.2023 г.). При отладке и тестировании использован компьютер IBM PC c процессором Сore i7 и ОЗУ 8 Гб. Набор тестовых функций, на которых проводилось программное моделирование, включал как одноэкстремальные, так и мультиэкстремальные функции: ● функция Розенброка f1(X) = xi ∈ [–30, 30]n, x* = (1, …, 1), f1(x*) = 0; ● сферическая функция f2(X) = ● функция Экли
xi Î [–32, 32]n, x* = (0, …, 0), f3(x*) = 0; ● функция Швефеля
xi Î [–100, 100]n, x* = (0, …, 0), f4(x*) = 0; ● сумма квадратов f5(X) = ● функция Растригина f6(X) = xi Î [–5,12; 5,12]n, x* = (0, …, 0), f6(x*) = 0; ● функция Соломона
xi Î [–100, 100]n, x* = (0, …, 0), f7(x*) = 0, где n – размерность функции; x* – оптимальное решение; fi(x*) – минимальное значение функции. Например, график функции Растригина пред- ставляет собой сочетание сферической и синусоидной функций с множеством локальных и одним глобальным минимумом, «банановая» функция Розенброка – большое медленно убы- вающее плато с глобальным минимумом внут- ри параболической сильно вытянутой поверхности, функция Швефеля является мультиэкстремальной с «непредсказуемым» глобальным минимумом; функция Соломона – непрерыв- ная, мультиэкстремальная, дифференцируемая. Подробное описание множества тестовых функций содержится в [11]. Результаты тестирования гибридного алгоритма МАКП-МАРС сопоставлялись с алгоритмами пчелиной колонии (Artificial Bee Colony, ABC), дифференциальной эволюции (Differen- tial Evolution, DE), роя частиц (Particle Swarm Optimization, PSO) [12−15], МАРС, MAKП. В экспериментах использовались следующие настройки параметров алгоритмов: ABC − параметр limit = 100; DE − параметр F ∈ [0,4; 1,0], параметр pm ∈ [0,0; 1,0]; PSO − коэффициенты обучения c1 = 2 и c2 = 2, вес w линейно уменьшается с 0,9 до 0,2 при увеличении числа итераций; МАКП − параметр PF = 0,7; МАРС − параметры kar = 0,6, lim = 1, N = 50, g = 20, gen = 1000. По каждой функции и каждому алгоритму осуществлялось 30 прогонов. Затем полученные результаты усреднялись.
В каждой клетке таблицы указаны среднее, медианное решение и стандартное отклонение от лучшего решения соответственно. Лучшие результаты выделены жирным шрифтом. Из таблицы видно, что гибридный алгоритм МАКП-МАРС обеспечивает лучшие результаты, нежели алгоритмы ABC, DE, PSO, MAKП, МАРС, практически для всех указанных функций. Также оценивалась статистическая значимость полученных результатов. С этой целью применялся Т-критерий суммы рангов Уилкоксона [17] для независимых выборок, найденных каждым из сравниваемых алгоритмов на 30 тестовых запусках, при уровне значимости 5 %. Значение Т < 0,05 рассматривалось как адекватное доказательство против нулевой гипотезы, которая отвергается. Предложенный гибридный алгоритм МАКП-МАРС превосходит конкурирующие, а экспериментальные результаты по нему являются статистически значимыми. Заключение Результаты, полученные гибридным алгоритмом МАКП-МАРС на одноэкстремальных и многоэкстремальных многомерных тестовых функциях, превосходят результаты конкурирующих алгоритмов и являются статистически значимыми. Это связано с достигаемым балансом между скоростью сходимости алгоритма и диверсификацией пространства поиска решений. Заслуживает внимания применение гибридного алгоритма МАКП-МАРС для решения задач динамической и стохастической оптимизации, многокритериальной оптимизации, мульти- модальной оптимизации, многомерной оптимизации, меметической оптимизации, в которой комбинируется множество поисковых алгоритмов, оптимизации и адаптации настроек параметров метаэвристик для достижения баланса между скоростью сходимости и диверсификацией пространства поиска решений. Список литературы 1. Родзин С.И. Современное состояние биоэвристик: классификация, бенчмаркинг, области применения // Изв. ЮФУ. Технич. науки. 2023. № 2. С. 280–298. doi: 10.18522/2311-3103-2023-2-280-298. 2. Rajwar K., Deep K., Das S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artificial Intelligence Review, 2023, vol. 56, pp. 13187–13257. doi: 10.1007/ s10462-023-10470-y. 3. Molina D., Poyatos J., Ser J.D. et al. Comprehensive taxonomies of nature- and bio-inspired optimization: Inspiration versus algorithmic behavior, critical analysis recommendations. Cognitive Computation, 2020, vol. 12, pp. 897–939. doi: 10.1007/s12559-020-09730-8. 4. Cuevas E., Fausto F., Gonzalez A. The locust swarm optimization algorithm. In: New Advancements in Swarm Algorithms: Operators and Applications. ISRL, 2019, vol. 160, pp. 139–159. doi: 10.1007/978-3-030-16339-6_5. 5. Camarena O., Cuevas E., Pérez-Cisneros M. et al. Ls-II: An improved locust search algorithm for solving optimization problems. Math. Problems in Eng., 2018, vol. 2018, art. 4148975. doi: 10.1155/2018/4148975. 6. Alekseev V. Application of artificial locust swarm routing algorithm for VFR flights planning. Math. Modeling, 2021, vol. 4, pp. 124–127. 7. Rodzin S., Kuliyev E., Zaporozhets D., Rodzina L., Rodzina O. Locust swarm optimization algorithm: A bio-heuristic for global optimization problem. In: LNNS. Proc. CSOC, 2023, vol. 722, pp. 670–678. doi: 10.1007/978-3-031-35311-6_64. 8. Luque-Chang A., Cuevas E., Fausto F. et al. Social spider optimization algorithm: modifications, applications, and perspectives. Math. Problems in Eng., 2018, vol. 2018, art. 6843923. doi: 10.1155/2018/6843923. 9. Evangeline D., Abirami T. Social spider optimization algorithm: Theory and its applications. IJITEE, 2019, vol. 8, no. 10, pp. 327–332. doi: 10.35940/ijitee.I8261.0881019. 10. Rodzin S., Rodzina L. Spider colony optimization algorithm: A bio-heuristic for global optimization problem. In: LNNS. Proc. CSOC, 2023, vol. 722, pp. 661–669. doi: 10.1007/978-3-031-35311-6_63. 11. Kerschke P., Trautmann H. Automated algorithm selection on continuous black-box problems by combining exploratory landscape analysis and machine learning. Evolutionary Comput., 2019, vol. 27, no. 1, pp. 99–127. doi: 10.1162/ evco_a_00236. 12. Long W., Wu T., Liang X., Xu S. Solving high-dimensional global optimization problems using an improved sine cosine algorithm. Expert Systems with Applications, 2019, vol. 123, pp. 108–126. doi: 10.1016/j.eswa.2018.11.032. 13. Dragoi E., Dafinescu V. Review of metaheuristics inspired from the animal kingdom. Math., 2021, vol. 9, no. 18, art. 2335. doi: 10.3390/math9182335. 14. Benítez-Hidalgo A., Nebro A.J., García-Nieto J., Oregi I., Ser J.D. jMetalPy: A Python framework for multi-objective optimization with metaheuristics. Swarm and Evolutionary Computation, 2019, vol. 51, art. 100598. doi: 10.1016/ j.swevo.2019.100598. 15. Tian Y., Cheng R., Zhang X., Jin Y. A MATLAB platform for evolutionary multi-objective optimization. IEEE Computational Intelligence Magazine, 2017, vol. 12, no. 4, pp. 73–87. doi: 10.1109/MCI.2017.2742868. 16. Иванов Д.К., Думина Д.С., Семенов Н.А. Определение весовых коэффициентов для аддитивной фитнес-функции генетического алгоритма // Программные продукты и системы. 2020. Т. 33. № 1. С. 47–53. doi: 10.15827/0236-235X.129.047-053. 17. Saha S., Seal D.B., Ghosh A., Dey K.N. A novel gene ranking method using Wilcoxon rank sum test and genetic algorithm. IJBRA, 2016, vol. 12, no. 3, рр. 263–279. doi: 10.1504/IJBRA.2016.078236. References 1. Rodzin, S.I. (2023) ‘Current state of bio heuristics: Classification, benchmarking, application areas’, Izv. SFedU. Eng. Sci., (2), pp. 280–298 (in Russ.). doi: 10.18522/2311-3103-2023-2-280-298. 2. Rajwar, K., Deep, K., Das, S. (2023) ‘An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges’, Artificial Intelligence Review, 56, pp. 13187–13257. doi: 10.1007/s10462-023-10470-y. 3. Molina, D., Poyatos, J., Ser, J.D. et al. (2020) ‘Comprehensive taxonomies of nature- and bio-inspired optimization: Inspiration versus algorithmic behavior, critical analysis recommendations’, Cognitive Computation, 12, pp. 897–939. doi: 10.1007/s12559-020-09730-8. 4. Cuevas, E., Fausto, F., Gonzalez, A. (2019) ‘The locust swarm optimization algorithm’, in New Advancements in Swarm Algorithms: Operators and Applications. ISRL, 160, pp. 139–159. doi: 10.1007/978-3-030-16339-6_5. 5. Camarena, O., Cuevas, E., Pérez-Cisneros, M. et al. (2018) ‘Ls-II: An improved locust search algorithm for solving optimization problems’, Math. Problems in Eng., 2018, art. 4148975. doi: 10.1155/2018/4148975. 6. Alekseev, V. (2021) ‘Application of artificial locust swarm routing algorithm for VFR flights planning’, Math. Modeling, 4, pp. 124–127. 7. Rodzin, S., Kuliyev, E., Zaporozhets, D., Rodzina, L., Rodzina, O. (2023) ‘Locust swarm optimization algorithm: A bio-heuristic for global optimization problem’, in LNNS. Proc. CSOC, 722, pp. 670–678. doi: 10.1007/978-3-031-35311-6_64. 8. Luque-Chang, A., Cuevas, E., Fausto, F. et al. (2018) ‘Social spider optimization algorithm: modifications, applications, and perspectives’, Math. Problems in Eng., 2018, art. 6843923. doi: 10.1155/2018/6843923. 9. Evangeline, D., Abirami, T. (2019) ‘Social spider optimization algorithm: Theory and its applications’, IJITEE, 8(10), pp. 327–332. doi: 10.35940/ijitee.I8261.0881019. 10. Rodzin, S., Rodzina, L. (2023) ‘Spider colony optimization algorithm: A bio-heuristic for global optimization problem’, in LNNS. Proc. CSOC, 722, pp. 661–669. doi: 10.1007/978-3-031-35311-6_63. 11. Kerschke, P., Trautmann, H. (2019) ‘Automated algorithm selection on continuous black-box problems by combining exploratory landscape analysis and machine learning’, Evolutionary Comput., 27(1), pp. 99–127. doi: 10.1162/evco_a_00236. 12. Long, W., Wu, T., Liang, X., Xu, S. (2019) ‘Solving high-dimensional global optimization problems using an improved sine cosine algorithm’, Expert Systems with Applications, 123, pp. 108–126. doi: 10.1016/j.eswa.2018.11.032. 13. Dragoi, E., Dafinescu, V. (2021) ‘Review of metaheuristics inspired from the animal kingdom’, Math., 9(18), art. 2335. doi: 10.3390/math9182335. 14. Benítez-Hidalgo, A., Nebro, A.J., García-Nieto, J., Oregi, I., Ser, J.D. (2019) ‘jMetalPy: A Python framework for multi-objective optimization with metaheuristics’, Swarm and Evolutionary Computation, 51, art. 100598. doi: 10.1016/j.swevo.2019.100598. 15. Tian, Y., Cheng, R., Zhang, X., Jin, Y. (2017) ‘A MATLAB platform for evolutionary multi-objective optimization’, IEEE Computational Intelligence Magazine, 12(4), pp. 73–87. doi: 10.1109/MCI.2017.2742868. 16. Ivanov, D.K., Dumina, D.S., Semenov, N.A. (2020) ‘Determination of weight coefficients for additive fitness function of genetic algorithm’, Software & Systems, 33(1), pp. 47–53 (in Russ.). doi: 10.15827/0236-235X.129.047-053. 17. Saha, S., Seal, D.B., Ghosh, A., Dey, K.N. (2016) ‘A novel gene ranking method using Wilcoxon rank sum test and genetic algorithm’, IJBRA, 12(3), рр. 263–279. doi: 10.1504/IJBRA.2016.078236. |
http://swsys.ru/index.php?id=5071&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Алгоритмы формирования управляющих воздействий в распределенных мультиагентных системах
- Многоагентный подход в системах информационной поддержки управленческих решений
- Алгоритм определения вероятности разрешения групповых воздушных объектов в районе аэродрома обзорными РЛС
- Постановка задачи исследования диффузионного перехода через границу шлак-металл в колонном реакторе и алгоритм ее решения
- Программное обеспечение навыковой системы принятия решений

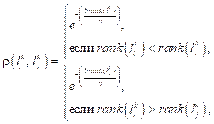 (3)
(3)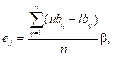
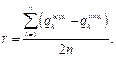
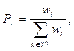
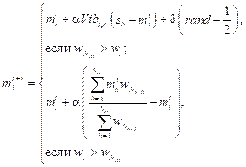
 представляет средневзвешенный вес самцов M в колонии.
представляет средневзвешенный вес самцов M в колонии.