Сегментация файлов неисполняемых форматов для выявления угроз нарушения информационной безопасности, реализуемых в форме эксплоитов
| Архипов А.Н. (diskpart111@mail.ru) - Московский государственный технический университет им. Н.Э. Баумана (ассистент кафедры), Москва, Россия, Кондаков С.Е. (sergeikondakov@list.ru) - Московский государственный технический университет им. Н.Э. Баумана (доцент), Москва, Россия, кандидат технических наук | |
| Ключевые слова: вредоносный код, компьютерный вирус, антивирусная защита информации, технологии обфускации, алгоритм сегментации, выявление эксплоитов, система защиты информации, компьютерная атака |
|
| Keywords: malware, computer virus, anti-virus information protection, obfuscation technologies, segmentation algorithm, exploit detection, information security system, computer attack |
|
|
|
|
Введение. Выявление угроз нарушения информационной безопасности, реализуемых посредством эксплоитов, является одним из приоритетных направлений, определенных в рамках функционирования и развития государственной системы обнаружения, предупреждения и ликвидации последствий компьютерных атак, направленных на информационные ресурсы Российской Федерации [1]. Решение указанной задачи достигается за счет совершенствования и разработки новых методов, алгоритмов и средств анализа файлов неисполняемых форматов, потенциально пригодных для внедрения в их состав эксплоитов. В ряде литературных источников, посвященных данной тематике, одним из основных этапов существующей методологии выявления эксплоитов в файлах неисполняемых форматов выделяется сегментация, которая осуществля- ется для возможности последующего углубленного анализа не всего файла целиком, а его фрагментов на наличие вредоносного кода. Анализируемый файл представляется в виде конечного множества блоков (фрагментов) определенной длины. В научных работах других исследователей условно можно выделить два основных подхода к решению данной задачи. Первый предполагает сегментацию файла на его структурные элементы в соответствии с форматом [2–4], второй, значительно чаще применяемый для решения задачи обнаружения вредоносного кода в файлах неисполняемых форматов как наиболее эффективный, – применение метода скользящего окна [5–7]. К основному недостатку обоих подходов можно отнести неоптимальность размеров получаемых сегментов (блоков), которые могут значительно отличаться от искомых в их составе элементов эксплоита, что значительно снижает эффективность обнаружения. Если при первом подходе размеры сегментов определяются структурой файла в соответствии со спецификацией на формат, то параметры скользящего окна подбираются либо экспертным методом, либо в рамках обучения модели бинарной классификации с использованием технологий машинного обучения и искусственного интеллекта и не обосновываются математически, например, на основе математического моделирования эксплоита и его составных частей [8, 9]. Также не учитывается специфика конкретного формата файла – его структурные особенности и предусмотренные методы преобразования данных (смена кодировки, сжатие и др.). Кроме того, не рассматривается возможность злоумышленника специально преобразовать элементы эксплоита к виду, сохраняющему заложенную функциональность, но затрудняющему анализ, – обфускации. Названные аспекты могут значительно снижать эффективность выявления угроз нарушения информационной безопасности, реализуемых посредством эксплоитов, в файлах неисполняемых форматов [10]. Указанные недостатки обусловливают актуальность разработки новых и/или совершенствование существующих методов и алгоритмов сегментации. В частности, в научной и практической литературе не представлен алгоритм сегментации, учитывающий строение формата неисполняемого файла, применение технологий обфускации и одновременно позволяющий осуществлять деление файла на сегменты математически обоснованной длины, обеспечивающей максимальную вероятность вхождения в их состав элементов эксплоита и минимизацию вероятности вхождения иных данных. Разработка этого алгоритма формирует результат, обладающий научной новизной. Постановка задачи Дано: X – множество файлов неисполняемых форматов с внедренными обфусцированными эксплоитами (вредоносные файлы) и без таковых (чистые файлы). Вербальная постановка научной задачи: разработать алгоритм разделения файлов неисполняемого формата на сегменты длины, позволяющей обеспечить максимизацию показателей эффективности сегментации. Формальная постановка научной задачи: разработать такой алгоритм Ac, что
где Выбор показателей и критериев их оценки Эксплоит структурно состоит из двух частей (модуля эксплуатации уязвимости и полезной нагрузки), которые обладают разными численными характеристиками [8, 9], отражающими их длины. Поэтому целесообразно разделить файл на сегменты размера z1 и z2, где сегменты длины z1 будут применяться для потенциального поиска содержимого модуля эксплуатации уязвимости, а z2 – полезной нагрузки эксплоита. Одновременно, учитывая, что по результатам сегментации необходимо получить сегменты длины, обеспечивающей максимальную вероятность вхождения в их состав элементов эксплоита и минимизацию вероятности вхождения иных данных, в качестве показателей эффективности сегментации определим следующие: w1 – вероятность события, при котором в сегмент bi длины z1 по результатам сегментации войдет только содержимое модуля эксплуатации эксплоита; w2 – вероятность события, при котором в сегмент bi длины z2 по результатам сегментации войдет только содержимое полезной нагрузки эксплоита. Указанные показатели могут быть найдены по формулам
где z1, z2 – размеры анализируемых сегментов в байтах; LS – размер модуля полезной нагрузки в байтах; LM – размер модуля эксплуатации в байтах. При идеальных значениях длин сегментов, получаемых при сегментации, показатели w1 и w2 будут равны 1, но в реальных условиях достижение указанных значений показателей маловероятно. Поэтому в качестве критерия оценки эффективности показателей сегментации определим требования, заданные в постановке задачи: max(w1)®1, max(w2)®1. (2) Разработка алгоритма сегментации Учитывая особенности построения эксплоита, отраженные в его математической модели, а именно нахождение элементов эксплоита в его структурообразующих блоках, на первом этапе необходимо разделить исследуемый файл на формирующие структурные элементы, используемые для его построения в соответствии со спецификацией на формат. Таким образом, на первом этапе Ac1 сегментации исследуемый файл представляется в виде конечного множества его структурных элементов в соответствии со спецификацией на конкретный формат:
где sp – структурные элементы сегментируемого файла; p – количество таких элементов. На втором этапе предлагаемого алгоритма структурные элементы исследуемого файла sp разделяем методом скользящего окна на сегменты длиной z1 и z2, где сегменты длины z1 будут для потенциального поиска содержимого модуля эксплуатации уязвимости, а z2 – полезной нагрузки эксплоита. С учетом изложенного на втором этапе Ac2 каждый из элементов sp, полученных на предыдущем этапе (3), будет сегментирован методом скользящего окна в соответствии с выражением
где a и e – число сегментов длины z1 и z2 соответственно. При этом их значения могут быть получены по следующим формулам: a = (LF – z1) + 1, e = (LF – z2) + 1, (5) где LF – размер анализируемого файла в байтах. Пусть числовые значения размера модуля полезной нагрузки и модуля эксплуатации в байтах для исследуемого множества файлов неисполняемых форматов с внедренными эксплоитами (вредоносные файлы) определяются неизвестной числовой функцией, определенной на множестве элементарных исходов. Тогда предсказать заранее, какое из своих значе- ний она примет, как правило, невозможно, можно лишь указать вероятность, с которой будет принято то или иное значение, или вероятность того, что ее значения будут находиться в каком-либо числовом промежутке. Тогда числовые значения размера модуля полезной нагрузки LS и модуля эксплуатации LM можно рассматривать как случайные величины, так как они удовлетворяют ее классическому определению [11]: заданы вероятностное пространство (W, F, P), числовая функция x(w) определена для всех w Î W, если для любого числа c выполняется условие {w Î W: x(w) £ c} Î F. С учетом выражений (1) и (2) значения длины сегментов в байтах должны удовлетворять условию z1 » LS, z2 » LM. (6) Случайная величина будет полностью описана с вероятностной точки зрения, если задать ее распределение, то есть точно указать, какой вероятностью обладает каждое из возможных событий. Этим будет установлен закон распределения случайной величины [11]. Поскольку реальный закон распределения неизвестен, получим его приближенные значения эмпирически. Для этого сформируем коллекцию файлов неисполняемых форматов, содержащих обфусцированные эксплоиты, из образцов, размещенных в открытом доступе (https://bazaar.abuse.ch/) (вредоносные файлы), и без таковых (чистые файлы), сгенерированные в автоматическом режиме с использованием штатных шаблонов приложений Microsoft Office. В качестве обфускаторов использованы свободно доступные на хостинге IT-проектов Github реализации, подходящие для автоматизированного запутывания большого количества исходных кодов. Для подтверждения наличия/отсутствия вре- доносного кода в сформированной коллекции применялись средства (технологии) антивирусной защиты информации, размещенные в открытом доступе (https://virustotal.com/). На базе полученной коллекции эксплоитов (2 500 шт.) проведем анализ значений размеров модуля полезной нагрузки LS и модуля эксплуатации LM и запишем их в виде рядов распределений. Построенные гистограммы плотности вероятности случайных величин (http://www.swsys.ru/ uploaded/image/2024-2/9.jpg), отображающих размеры упомянутых элементов эксплоита, позволяют выдвинуть предположение о нормальности распределений данных случайных величин. Для подтверждения данного предположения воспользуемся специализированными статистическими методами Колмогорова–Смирнова и Шапиро–Уилка [12, 13]. По результатам выполнения указанных статистических тестов получены следующие значения контрольных критериев: D1 = 0.01662, D2 = 0.01601, W1 = 0.9992, W2 = 0.9987. Отличия полученной эмпирически и эталонной (нормальной) функций распределений при их проверке статистическими методами Колмогорова–Смирнова и Шапиро–Уилка мож- но увидеть на построенных графиках (http:// www.swsys.ru/uploaded/image/2024-2/10.jpg). На основании полученных результатов можно сделать вывод о том, что случайные величины значений размера модуля полезной нагрузки LS и модуля эксплуатации LM являются нормально распределенными с уровнем значимости, равным 0.05. Поэтому с учетом критериев (2) значения для параметров z1 и z2 будут следующие: z1 » LS » ES, z2 » LM » EM, (7) где ES и EM – эмпирические математические ожидания значений размера модуля полезной нагрузки LS и модуля эксплуатации LM соответственно. Таким образом, сегментацию структурных элементов исследуемого файла sp будем осуществлять на блоки размера z1 = 1 548 байт и z2 = 466. Обобщая полученные результаты, запишем алгоритм сегментации файлов неисполняемых форматов с указанием конкретных параметров сегментирования с учетом выражений (3)–(5) и (7):
Результаты исследования эффективности применения предлагаемого алгоритма С формальной точки зрения выявление угроз нарушения информационной безопасности, реализуемых посредством эксплоитов, сводится к решению научной задачи бинарной класси- фикации файлов неисполняемых форматов на безопасные и вредоносные. С учетом изложенного в качестве метода оценки эффективности бинарной классификации выберем ROC-анализ [14–16]. В качестве показателя оценки эффективности бинарной классификации определим
где q1 – чувствительность, q2 – специфичность, которые вычисляются по формулам
где TP – число верно классифицированных вредоносных объектов; FN – число объектов, классифицированных как отрицательные (ошибка I рода); TN – число верно классифицированных безопасных объектов; FP – число объектов, классифицированных как положительные (ошибка II рода). В качестве критерия оценки эффективности используем условие, предусмотренное в методе: max(q) → 1. Описанный алгоритм сегментации реализован в программе для ЭВМ AntigenExploits (Свидетельство о госрегистрации № 2023687464), разработанной авторами в качестве эмпирической реализации методики выявления угроз нарушения информационной безопасности, реализуемых посредством эксплоитов. Исследования эффективности применения предлагаемого алгоритма проведены с использованием указанной программы. Эксперименты проводились в следующем порядке. 1. Подготовка тестовой выборки из 2 000 файлов неисполняемых форматов, не используемых при разработке алгоритма сегментации, содержащей файлы с внедренными эксплоитами (вредоносные файлы – 1 000 образцов) и без таковых (безопасные файлы – 1 000 образцов). 2. Анализ тестовой выборки с помощью существующих отечественных средств антиви- русной защиты информации, включенных в реестр российского программного обеспечения, а также в программы AntigenExploits. 3. Анализ результатов экспериментального исследования (см. таблицу). Результаты экспериментального исследования Experimental study results
Результаты оценки показали, что алгоритм сегментации, предлагаемый авторами, в конкретном исследовании позволил повысить эффективность выявления угроз нарушения информационной безопасности, реализуемых посредством обфусцированных эксплоитов, по сравнению с существующими средствами антивирусной защиты информации более чем на 7 %. Заключение В статье представлен алгоритм сегментации файлов неисполняемых форматов, применимый в задаче выявления эксплоитов, определяющий порядок, применяемые методы и численные параметры сегментации, обоснованные математически. Алгоритм является универсальным и позволяет разбивать любые файлы неисполняемых форматов на сегменты наилучшей длины, обеспечивающей максимальную вероятность вхождения в их состав элементов эксплоита и минимизацию вероятности вхождения иных данных. При этом сегментирование файла неисполняемого формата предложенным алгоритмом применимо для выявления эксплоитов, подвергшихся процедуре обфускации. Указанные аспекты отличают представленный алгоритм сегментации от существующих аналогов. В качестве направления для дальнейших исследований в данной области целесообразно рассмотреть возможность оптимизации шага (сдвига по фазе) предложенного алгоритма сегментации. Список литературы 1. Ланецкая А.Ю., Александрова Е.Н. Современные угрозы информационной безопасности // Междунар. журнал гуманитарных и естественных наук. 2022. № 7-2. С. 192–195. 2. Zhou X., Pang J. Expdf: Exploits detection system based on machine-learning. Int. J. of Computational Intelligence, 2019, vol. 12, no. 2, pp. 1019–1028. doi: 10.2991/ijcis.d.190905.001. 3. Falah A., Pan L., Abdelrazek M., Doss R. Identifying drawbacks in malicious PDF detectors. In: CCIS. Proc. FNSS, 2019, vol. 878, pp. 128–139. doi: 10.1007/978-3-319-94421-0_10. 4. Kumar R., Geetha S. Malware classification using XGboost-gradient boosted decision tree. ASTES J., 2020, vol. 5, no. 5, pp. 536–549. doi: 10.25046/aj050566. 5. Yousefi-Azar M., Varadharajan V., Hamey L., Chen S. Mutual information and feature importance gradient boosting: Automatic byte n-gram feature reranking for Android malware detection. Software: Practice and Experience, 2021, vol. 51, no. 7, pp. 1518–1539. doi: 10.1002/spe.2971. 6. Jeong Y.S., Woo J., Kang A.R. Malware detection on byte streams of hangul word processor files. Appl. Sci., 2019, vol. 9, no. 23, art. 5178. doi: 10.3390/app9235178. 7. Kang A.R., Jeong Y.S., Kim S.L., Woo J. Malicious PDF detection model against adversarial attack built from benign PDF containing JavaScript. Appl. Sci., 2019, vol. 9, no. 22, art. 4764. doi: 10.3390/app9224764. 8. Кондаков С.Е., Архипов А.Н. Математическая модель эксплоита, внедренного в файл неисполняемого формата // Изв. ИИФ. 2023. Т. 69. № 3. С. 93–96. 9. Архипов А.Н., Кондаков С.Е. Разработка математической модели эксплоита, внедренного в файл неисполняемого формата, с учетом полезной нагрузки // Приборы. 2023. № 11. С. 39–46. 10. Архипов А.Н., Пиков В.А., Кабаков В.В. Порядок и результаты экспериментальных исследований влияния обфускации на качество выявления угроз информационной безопасности, реализуемых посредством эксплоитов, в файлах неисполняемых форматов // Вопросы защиты информации. 2023. № 2. С. 32–37. 11. Феллер В. Введение в теорию вероятностей и ее приложения; [пер. с англ.]. М.: Мир, 1984. Т. 1. 528 с. 12. Леман Э. Проверка статистических гипотез; [пер. с англ.]. М.: Наука, 1979. 408 с. 13. Shapiro S.S., Wilk M.B. An analysis of variance test for normality (complete samples). Biometrika, 1965, vol. 52, no. 3-4, pp. 591–611. doi: 10.1093/BIOMET/52.3-4.591. 14. Брюс П., Брюс Э. Практическая статистика для специалистов Data Science; [пер. с англ.]. СПб: БХВ-Петербург, 2018. 304 с. 15. Старовойтов В.В., Голуб Ю.И. Сравнительный анализ оценок качества бинарной классификации // Информатика. 2020. Т. 17. № 1. С. 87–101. doi: 10.37661/1816-0301-2020-17-1-87-101. 16. Vujovic Ž.Ð. Classification model evaluation metrics. IJACSA, 2021, vol. 12, no. 6, pp. 599–606. doi: 10.14569/ IJACSA.2021.0120670. References 1. Lanetskaya, A.Yu., Aleksandrova, E.N. (2022) ‘Modern threats to information security’, Int. J. of Humanities and Natural Sci., (7-2), pp. 192–195 (in Russ.). 2. Zhou, X., Pang, J. (2019) ‘Expdf: Exploits detection system based on machine-learning’, Int. J. of Computational Intelligence, 12(2), pp. 1019–1028. doi: 10.2991/ijcis.d.190905.001. 3. Falah, A., Pan, L., Abdelrazek, M., Doss, R. (2019) ‘Identifying drawbacks in malicious PDF detectors’, in CCIS. Proc. FNSS, 878, pp. 128–139. doi: 10.1007/978-3-319-94421-0_10. 4. Kumar, R., Geetha, S. (2020) ‘Malware classification using XGboost-gradient boosted decision tree’, ASTES J., 5(5), pp. 536–549. doi: 10.25046/aj050566. 5. Yousefi-Azar, M., Varadharajan, V., Hamey, L., Chen, S. (2021) ‘Mutual information and feature importance gradient boosting: Automatic byte n-gram feature reranking for Android malware detection’, Software: Practice and Experience, 51(7), pp. 1518–1539. doi: 10.1002/spe.2971. 6. Jeong, Y.S., Woo, J., Kang, A.R. (2019) ‘Malware detection on byte streams of hangul word processor files’, Appl. Sci., 9(23), art. 5178. doi: 10.3390/app9235178. 7. Kang, A.R., Jeong, Y.S., Kim, S.L., Woo, J. (2019) ‘Malicious PDF detection model against adversarial attack built from benign PDF containing JavaScript’, Appl. Sci., 9(22), art. 4764. doi: 10.3390/app9224764. 8. Kondakov, S.E., Arkhipov, A.N. (2023) ‘Mathematical model of an exploit embedded in a nonexecutable file’, Proc. of IEP, 69(3), pp. 93–96 (in Russ.). 9. Arkhipov, A.N., Kondakov, S.E. (2023) ‘Development of a mathematical model of an exploit embedded in a non-executable file format, taking into account the payload’, Instruments, (11), pp. 39–46 (in Russ.). 10. Arkhipov, A.N., Pikov, V.A., Kabakov, V.V. (2023) ‘The order and results of experimental studies of the influence of obfuscation on the quality of detecting information security threats implemented through exploits in files of non-executable formats’, Information Security Questions, (2), pp. 32–37 (in Russ.). 11. Feller, W. (1957) An Introduction to Probability Theory and its Applications, NY: John Wiley & Sons, 526 p. (Russ. ed.: (1984) Moscow, 528 p.). 12. Lehmann, E.L. (1959) Testing Statistical Hypotheses, NY: John Wiley & Sons, 388 p. (Russ. ed.: (1979) Moscow, 408 p.). 13. Shapiro, S.S., Wilk, M.B. (1965) ‘An Analysis of Variance Test for Normality (Complete Samples)’, Biometrika, 52(3/4), pp. 591–611. doi: 10.1093/BIOMET/52.3-4.591. 14. Bruce, P., Bruce, E. (2017) Practical Statistics for Data Scientists, CA: O’Reilly Media Publ., 317 p. (Russ. ed.: (2018) St. Petersburg, 304 p.). 15. Starovoytov, V.V., Golub, Yu.I. (2020) ‘Comparative study of quality estimation of binary classification’, Informatics, 17(1), pp. 87–101 (in Russ.). doi: 10.37661/1816-0301-2020-17-1-87-101. 16. Vujovic, Ž.Ð. (2021) ‘Classification model evaluation metrics’, IJACSA, 12(6), pp. 599–606. doi: 10.14569/IJACSA.2021.0120670. |
http://swsys.ru/index.php?id=5076&lang=%2C&page=article |
|
Perhaps, you might be interested in the following articles of similar topics:
- Система поддержки принятия решений по защите информации «ОАЗИС»
- Метод формирования множеств альтернативных вариантов построения подсистем, входящих в состав системы защиты от компьютерных атак
- Определение авторства вредоносного кода с использованием метода сжатия данных
- Проблемы обработки статистики сетевого трафика для обнаружения вторжений в существующих информационных системах
- Обнаружение аномалий сетевого трафика методом глубокого обучения

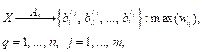
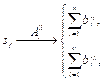 (4)
(4)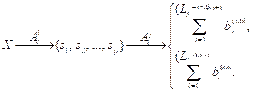 (8)
(8)