Введение. При решении исследовательских и инженерных задач в области радиотехники и электроники часто возникает необходимость сравнения двух наборов данных (например, результатов компьютерного моделирования и натурного эксперимента). Для этого, как правило, выполняется расчет погрешностей или отклонений, которые, однако, не всегда дают адекватную оценку сходимости результатов, особенно, если сопоставляемые данные описывают сложные нелинейные зависимости.

Для сопоставления двух наборов данных предложен метод валидации выделением особенностей [1–3], известный в зарубежной литературе как feature selective validation method (далее – метод FSV). Данный метод позволя- ет получить количественную оценку качества совпадения двух наборов данных и избавиться от элемента субъективности в процессе этой оценки. После своего появления метод FSV быстро завоевал популярность и стал широко использоваться для верификации математических моделей в области вычислительной электродинамики [4–6] и в других сферах [7, 8]. Метод также был включен в знаковый зару- бежный стандарт IEEE STD 1597, регламентирующий процедуры тестирования математического и программного обеспечения, предназначенного для электромагнитного моделирования. Несмотря на широкую распространенность  и удобство метода FSV, отечественные исследователи и разработчики его практически не применяют. Цель данной работы – восполнить этот пробел за счет демонстрации примеров использования метода FSV, а также разработки простого открытого программного средства (ПС), реализующего этот метод.

Алгоритм сопоставления данных  методом FSV

Алгоритм сопоставления данных с помощью метода FSV включает четыре основных этапа: предобработка данных, их разделение на диапазоны, расчет мер разности между наборами данных, интерпретация рассчитанных мер для построения оценочной гистограммы (рис. 1).

На этапе предобработки осуществляются импорт сопоставляемых наборов данных, их интерполяция (для получения одинакового числа отсчетов) и последующее применение  к ним быстрого преобразования Фурье. После быстрого преобразования Фурье число отсчетов в наборах остается таким же, как и в исходных данных до преобразования.

На втором этапе производится разделение данных, полученных после быстрого преобразования Фурье, на три диапазона: DC (постоянный ток), Lo (низкие частоты) и Hi (высокие частоты). К диапазону DC обычно относят все отсчеты с номерами i от 1 до 5, причем данные, соответствующие этим отсчетам, при дальней- шей оценке не используются, то есть удаляются из наборов. Для определения границы между диапазонами Lo и Hi сначала в каждом из наборов данных определяются так называемые точки 40 % (i40 %). Каждая такая точка соответствует номеру отсчета, на котором сумма всех значений данных на предшествующих ему отсчетах равна 40 % от общей суммы S всех значений в наборе данных. Затем из двух найденных точек i40 % выбирается наибольшая, которая назначается в качестве точки ibp, разделяющей диапазоны Lo и Hi. Если исходные наборы содержат K отсчетов, в результате получим Lo = X {6, …, ibp} и Hi = X {ibp+1, …, K}. В завершение этапа разделения данных к полученным диапазонам Lo и Hi применяется обратное преобразование Фурье.

Следует отметить, что описанный метод разделения данных на диапазоны не является единственно возможным и тем более оптимальным. Так, помимо жесткого разбиения наборов данных, широко распространены методы разделения на основе фильтрации, в результате которой в диапазоны Lo и Hi включаются пять или девять общих точек (отсчетов) [2].

На следующем этапе отсчеты, попавшие  в диапазоны Lo и Hi, используются для расчета мер разности между исходными наборами данных (процедура расчета подробно изложена  в работе [9]). Так, для сопоставления наборов по амплитудному критерию (тренду) применяется так называемая мера разницы амплитуд (amplitude difference measure, ADM). Различие между скоростями изменения наборов данных оценивается по значениям меры разности характеристик (feature difference measure, FDM). Для общей оценки сходимости часто используется глобальная мера разности (global difference measure, GDM), определяемая для n-го отсчета как

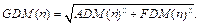
В рамках заключительного этапа с помощью вычисленных значений мер ADM, FDM или GDM строится доверительная гистограмма, отображающая оценку согласованности двух наборов данных. Для построения  гистограммы применяется таблица интерпретации результатов метода FSV, устанавлива-ющая соотношения между значениями рассчитанной меры и качественными категориями от «очень плохо» до «отлично». В алгоритме  из рисунка 1 для получения оценочной гистограммы на этапе постобработки создаются шесть счетчиков (согласно числу качественных категорий), которые фиксируют резуль- таты проверки каждого из N вычисленных значений GDM, FDM или ADM по таблице. На основе информации из счетчиков формируется, а затем выводится оценочная гистограмма с процентной шкалой.

Интерпретация результатов метода FSV

Interpretation of FSV results

Разработка ПС

На базе алгоритма (рис. 1) разработано ПС для сопоставления двух наборов данных методом FSV (https://talgat.org/). Разработка выполнялась на базе MS Windows 10 с использованием возможностей фреймворка Qt Creator на языке C++. Также был применен ряд вспомогательных библиотек, таких как Armadillo (для реализации процедур быстрого преобразования Фурье и обратного преобразования Фурье), QtXlsx (для работы с файлами excel) и QCustomPlot (для построения и визуализации исход- ных данных и оценочных гистограмм). На рисунке 2 приведена UML-диаграмма компонентов созданного ПС. Для объединения работы всех компонентов используется файл Main, управляющий вызовом функций и обработкой данных, а также реализующий процедуры логирования. Основой модуля является компонент FSV, выполняющий функции импорта  и экспорта данных (из директории Source Vector), вычислений по методу FSV, а также построения оценочных гистограмм и рассчитанных мер для их визуализации в графическом интерфейсе (UI). Чтение и запись файлов реализуются базовыми средствами операционной системы.

Разработанное ПС также содержит ряд вспомогательных классов. Так, класс HelpWindow отвечает за отображение справочной информации по работе с ПС, а ConfParams – за конфигурирование (изменение стиля) графического интерфейса.

Для разработанных ПС установлены следующие минимальные системные требования: операционная система Windows 7,8 или 10;  78 Мб свободной памяти на диске; объем ОЗУ не менее 2 Гб; двухъядерный процессор с тактовой частотой не менее 2 ГГц; наличие устройств ввода (клавиатура, мышь) и вывода (монитор).

На рисунке 3 показан графический интерфейс разработанного ПС. В верхней части окна располагаются переключатели между вкладками, содержащими исходные данные, рассчитанные значения ADM, FDM и GDM и их гистограммы. Вкладка «Главная» включает в себя элементы управления, необходимые для импорта наборов данных в ПС. Данные могут быть загружены в популярных текстовых  и табличных форматах: txt, csv, xls или xlsx. Кроме того, доступна загрузка файлов в формате SnP (Touchstone), широко применяющемся в программах для электромагнитного  и схемотехнического моделирования, а также  в векторных и скалярных анализаторах цепей. Для загрузки в ПС данные должны быть разделены по двум отдельным файлам (допускается загрузка двух файлов разных форматов) либо объединены в один, содержащий несколько столбцов. Для удобной работы в ПС добавлено окно для предварительного просмотра содержимого импортируемых файлов (http://www. swsys.ru/uploaded/image/2024-3/7.jpg), а также реализован алгоритм кусочно-линейной интерполяции, позволяющий сравнивать наборы данных с разным числом отсчетов.

В правой части вкладки «Главная» доступен выбор типа фильтра, использующегося при разделении загруженных наборов данных на диапазоны. Всего в ПС реализованы четыре варианта разделения данных, в том числе предусматривающие наличие общих точек (отсчетов) в диапазонах Lo и Hi. Для наглядности выбранная пользователем процедура разделения данных демонстрируется в схематичном виде на графике, расположенном во вкладке AFR filter.

Результаты обработки данных методом FSV отображаются во вкладках ADM Graph–GDM Hist, каждая из которых имеет встроенную графическую сцену для вывода значений мер или их гистограмм (http://www.swsys.ru/uploaded/ image/2024-3/8.jpg). Для настройки этих сцен  в ПС реализованы функции масштабирования, визуализации линий сетки, отображения резуль- татов в процентной шкале и пр. С целью последующего использования результатов вычислений их можно сохранить в табличных форматах csv, xls, xlsx или экспортировать из ПС в виде растровых изображений в формате jpg.

Примеры использования

Для демонстрации возможностей метода FSV и разработанного ПС выполнено сравнение четырех разных наборов данных. Во всех случаях сходимость оценивалась по гистограм- ме GDM, а для разделения наборов на диапазоны применялась фильтрация с пятью общими точками. Первые сопоставленные наборы показаны на рисунке 4а. Данные взяты из [10]  и представляют собой частотные зависимости напряжения U на одном из проводников многосвязной линии передачи, полученные с помощью численного метода конечных элементов  и гибридной модели, сочетающей квазистатический и схемотехнический виды анализа. Из рисунка 4а видно, что до отсчета 600 данные отлично согласуются. С увеличением номера отсчета появляются различия по амплитуде  и положениям локальных минимумов, что усложняет оценку сходимости. При этом в целом различия выглядят адекватными и допустимыми для двух принципиально разных подходов к моделированию. Эта качественная оценка подтверждается гистограммой GDM, показанной на рисунке 4б. Так, видно, что преимущественно (для 81 % отсчетов) данные сходятся с оценками «отлично», «очень хорошо»  и «хорошо». Причем в категорию «очень хорошо» попадает до 40 % данных из наборов.

Следующие наборы данных, показанные на рисунке 5а, взяты из [11]. Они описывают частотные зависимости эффективности экранирования прямоугольного металлического кор- пуса со щелью, полученные методом конечных элементов и полуаналитической моделью. Видно, что до отсчета 500 данные хорошо согласуются. Затем в диапазоне от 500 до 1 000 совпадают только точки минимумов, а по амплитудам имеются значительные различия. При этом во всех последующих отсчетах  (от 1 000 до 1 200) наборы существенно различаются. В результате получение однозначной качественной оценки сходимости результатов не представляется возможным. Однако оценку можно получить с использованием метода FSV. Так, из гистограммы GDM (рис. 5б), видно, что почти для 30 % отсчетов совпадение оценивается как «удовлетворительное». При этом к категориям «отлично» и «очень хорошо» относятся всего лишь 24 % от общего числа данных.

Для третьего примера использованы данные из [12], описывающие частотные зависимости нормированного коэффициента передачи |S21| между концами кабеля, находящегося внутри объемного резонатора, полученные моделированием и экспериментально (посредством из- мерений). Выбранные наборы данных показаны на рисунке 6а. Видно, что результаты моделирования и эксперимента очень близки, однако на измеренной частотной зависимости |S21| имеется множество осцилляций, которые не позволяют дать однозначную оценку сходимости данных без использования метода FSV. Гистограмма GDM, полученная для исследуемых наборов, представлена на рисунке 6б. Видно, что почти для 90 % отсчетов данные согласуются с оценками «отлично», «очень хорошо» и «хорошо». При этом оставшиеся 10 % отнесены к категории «удовлетворительно»,  а данные, оцениваемые «плохо» и «очень плохо», в наборах отсутствуют.

Последние использованные наборы данных показаны на рисунке 7а. Они представляют собой частотные зависимости модуля напряженности электрического поля |E|, полученные при моделировании и измерениях снаружи экранирующего корпуса с излучающей антенной внутри. Видно, что положения максимумов |E| на зависимостях, полученных разными подходами, сходятся, но имеются расхождения  по их амплитудам. При этом качественная оценка сходимости данных осложняется из-за их большого динамического диапазона.

Гистограмма GDM, соответствующая результатам моделирования и измерений |E|, показана на рисунке 7б. Видно, что для 27 % отсчетов совпадение оценивается как «очень хорошее». При этом почти 35 % отчетов отнесено  к категориям «удовлетворительно», «плохо»  и «очень плохо».

Заключение

Приведены теоретические основы и алгоритм работы метода FSV, предназначенного для количественной оценки совпадения двух наборов данных. Представлены результаты разработки ПС на основе метода FSV. Для демонстрации возможностей этого метода и ПС сопоставлены четыре набора данных. В резуль- тате показано, что разработанное ПС и метод FSV позволяют получить достоверные количественные оценки сходимости двух наборов данных даже тогда, когда их качественное ви- зуальное сопоставление затруднительно. По-этому метод FSV может быть рекомендован  к использованию, как минимум, специалистам, разрабатывающим математическое и програм- мное обеспечение для моделирования сложных технических систем. Отметим, что в настоящий момент представленное ПС доступно для свободного скачивания на сайте лаборатории разработчика.

Список литературы

1. Duffy A., Orlandi A. The influence of data density on the consistency of performance of the feature selective validation (FSV) technique. ACES, 2006, vol. 21, no. 2, pp. 164–172.

2. Duffy A., Zhang G. FSV: State of the art and current research fronts. IEEE Electromagnetic Compatibility Magazine, 2020, vol. 9, no. 3, pp. 55–62. doi: 10.1109/MEMC.2020.9241552.

3. Bongiorno J., Mariscotti A. Uncertainty and sensitivity of the feature selective validation (FSV) method. Electronics, 2022, vol. 11, no. 16, art. 2532. doi: 10.3390/electronics11162532.

4. Kadem K., Benyoubi F., Bensetti M. et al. An efficient method for dimensioning magnetic shielding for an induction electric vehicle charging system. PIER, 2021, vol. 170, pp. 153–167. doi: 10.2528/PIER21031903.

5. Zhang G., Duffy A. Applying FSV to the comparison of return path integrity in high speed circuit designs. IEEE  L-EMCPA, 2021, vol. 3, no. 2, pp. 78–81. doi: 10.1109/LEMCPA.2021.3064420.

6. Rabat A., Bonnet P., Drissi K.E.K., Girard S. An analytical evaluation of the shielding effectiveness of enclosures containing complex apertures. IEEE Access, 2021, vol. 9, pp. 147191–147200. doi: 10.1109/ACCESS.2021.3123441.

7. Stöhr T., Rasek G.A., Murthy N.S. Agreement quantification of a numerical EMC computer model and test infrastructure for the HV power train emissions for an electric vehicle. Proc. EMC Europe, 2023, pp. 1–6. doi: 10.1109/EMCEurope57790.2023.10274221.

8. Zhang G., Zappala D., Crabtree C., Donaghy-Spargo C., Hogg S., Duffy A. Validation of a non-contact technique for torque measurements in wind turbines using an enhanced transient FSV approach. Measurement, 2020, vol. 151,  art. 107261. doi: 10.1016/j.measurement.2019.107261.

9. Шайманов Н.Ю., Осинцев А.В., Иванов А.А. Об использовании метода FSV в задачах электромагнитной совместимости // Электронные средства и системы управления: мат. конф. 2023. С. 50–52.

10. Алхадж Хасан А. Виртуальные испытания структуры с модальным резервированием в системе TALGAT // СИБРЕСУРС: мат. конф. 2022. С. 102–107.

11. Ivanov A.A., Demakov A.V., Komnatnov M.E., Gazizov T.R. Semi-analytical approach for calculating shielding effectiveness of an enclosure with a filled aperture. Electrica, 2022, vol. 22, no. 2, pp. 220–225. doi: 10.54614/electrica.2022.21152.

12. Williams A.J.M., Benson T.M., Duffy A.P. Determining the accuracy of TLM in simulating the behaviour of resonant cavities with arbitrary dielectric loading. IJE, 1997, vol. 83, no. 5, pp. 645–660. doi: 10.1080/002072197135201.

References

1. Duffy, A., Orlandi, A. (2006) ‘The influence of data density on the consistency of performance of the feature selective validation (FSV) technique’, ACES, 21(2), pp. 164–172.

2. Duffy, A., Zhang, G. (2020) ‘FSV: State of the art and current research fronts’, IEEE Electromagnetic Compatibility Magazine, 9(3), pp. 55–62. doi: 10.1109/MEMC.2020.9241552.

3. Bongiorno, J., Mariscotti, A. (2022) ‘Uncertainty and sensitivity of the feature selective validation (FSV) method’, Electronics, 11(16), art. 2532. doi: 10.3390/electronics11162532.

4. Kadem, K., Benyoubi, F., Bensetti, M. et al. (2021) ‘An efficient method for dimensioning magnetic shielding for an induction electric vehicle charging system’, PIER, 170, pp. 153–167. doi: 10.2528/PIER21031903.

5. Zhang, G., Duffy, A. (2021) ‘Applying FSV to the comparison of return path integrity in high speed circuit designs’, IEEE L-EMCPA, 3(2), pp. 78–81. doi: 10.1109/LEMCPA.2021.3064420.

6. Rabat, A., Bonnet, P., Drissi, K.E.K., Girard, S. (2021) ‘An analytical evaluation of the shielding effectiveness of enclosures containing complex apertures’, IEEE Access, 9, pp. 147191–147200. doi: 10.1109/ACCESS.2021.3123441.

7. Stöhr, T., Rasek, G.A., Murthy, N.S. (2023) ‘Agreement quantification of a numerical EMC computer model and test infrastructure for the HV power train emissions for an electric vehicle’, Proc. EMC Europe, pp. 1–6. doi: 10.1109/EM-CEurope57790.2023.10274221.

8. Zhang, G., Zappala, D., Crabtree, C. Donaghy-Spargo, C., Hogg, S., Duffy, A. (2020) ‘Validation of a non-contact technique for torque measurements in wind turbines using an enhanced transient FSV approach’, Measurement, 151, art. 107261. doi: 10.1016/j.measurement.2019.107261.

9. Shaymanov, N.Yu., Osintsev, A.V., Ivanov, A.A. (2023) ‘On the use of FSV method in electromagnetic compatibil-ity problems’, Proc. Conf. Electronic Aids and Control Systems, pp. 50–52 (in Russ.).

10. Alhaj Hasan, A. (2022) ‘Virtual experiment of a structure with modal reservations in the TALGAT system’, Proc. Conf. SIBRESOURCE, pp. 102–107 (in Russ.).

11. Ivanov, A.A., Demakov, A.V., Komnatnov, M.E., Gazizov, T.R. (2022) ‘Semi-analytical approach for calculating shielding effectiveness of an enclosure with a filled aperture’, Electrica, 22(2), pp. 220–225. doi: 10.54614/elec-trica.2022.21152.

12. Williams, A.J.M., Benson, T.M., Duffy, A.P. (1997) ‘Determining the accuracy of TLM in simulating the behaviour of resonant cavities with arbitrary dielectric loading’, IJE, 83(5), pp. 645–660. doi: 10.1080/002072197135201.