Введение. Проблемы исследования сложных технических систем (СТС) с разнотипными информационными потоками остаются актуальными. Так, на примере задачи обеспечения охраны протяженного периметра они рассмотрены в работе [1]. Особое внимание уделяется решению практической задачи планирования совместных действий объектов таких систем, для моделирования которых целесообразно использование GH-графов (Graph-Hypergraph) - нечетких графов с множественными и разнотипными связями [2]) и определенных алгоритмических средств, в том числе синтеза алгоритма пропорционального разделения GH-графа и средств вычисления его метрик. Традиционно ориентированные связи графа названы дугами, неориентированные – ребрами, а в общем случае использован термин «связи».
Для вычисления метрических характеристик графа (подграфа), таких как радиус, диаметр и другие, необходимо сформировать матрицу расстояний между парами вершин графа. Сложности вычисления расстояний на GH-гра- фах обусловливают синтез новых или модификацию известных алгоритмов поиска кратчайших путей. Решению этой задачи в основном и посвящена данная работа.
Известно большое количество алгоритмов поиска кратчайшего пути в графе, в том числе алгоритм Ли, алгоритм Дейкстры, алгоритмы Форда-Беллмана и Флойда-Уоршелла.
Оригинальный алгоритм Ли не может быть применен к взвешенным графам. Для решения этой проблемы в работе [3] предлагаются средства перехода от взвешенного к невзвешенному графу, что существенно увеличивает ко- личество вершин графа, а следовательно, приводит к росту времени вычислений.
Алгоритм Дейкстры не может работать с отрицательными весами на ребрах графа, к тому же вычислительная сложность такого алгорит- ма и большей части его модификаций составляет O (n2 + m), где n и m – количество вершин и ребер графа соответственно [4, 5]. Вычислительная сложность алгоритма Флойда-Уоршелла имеет более высокое численное значение – O (n3) [6].
Алгоритм Форда-Беллмана [7, 8] имеет более низкую оценку вычислительной сложности по сравнению с рассмотренными алгоритмами, а именно – O (n × m) [6], и позволяет работать с ребрами отрицательного веса в ориентированных или неориентированных графах. Хотя в нечетких графах отрицательные веса ребер не используются, эта функция может быть полезна в будущем.
Для поиска кратчайших путей в графах с кратными однотипными ребрами известен алгоритм, предложенный в работе [9], но использование его для решения поставленной в данном исследовании задачи вызывает затруднения ввиду проблемы разнотипности ребер.
В представленной статье рассматривается проблема моделирования больших и сложных технических систем, а потому их графовая модель может быть довольно объемной по количеству вершин и связей и, кроме того, динамически изменяющейся во времени. Все это обосновано анализом существующих алгоритмов поиска кратчайших путей на больших и динамически изменяющихся графах.
Примеры таких алгоритмов рассмотрены в работах [10-12]. В общем случае описанные в них подходы можно сформулировать так: большой граф случайным образом разбивается сначала на кластеры, потом в случае необходимости – на подкластеры, а затем выполняется перекомпоновка полученных кластеров (подкластеров) с учетом определенных требований, например, в зависимости от компоненты связности графа или других параметров [10]. Вычисление кратчайших путей происходит внутри кластеров (подкластеров), а затем между ними, что приводит к получению итоговой матрицы расстояний. Однако предложенные подходы не учитывают разнотипные связи в GH-графах, а также характеризуются избыточностью действий по перекомпоновке кластеров, что влечет за собой рост временных затрат на вычисления. Тем не менее подходы по разделению графа на части могут быть полезны в данном исследовании.
Обзор известных алгоритмов поиска кратчайшего пути в графе позволяет сделать следующие выводы. Наиболее подходящим алгоритмом поиска кратчайших путей для использования в GH-графе является алгоритм Форда-Беллмана, для которого имеются реализации матричным и списковым способами представления графа. Однако использование смешанных однотипных, разнотипных и множественных связей в виде вектора в GH-графе [13], а также возможность использования графов больших размеров обусловливают необходимость модификации оригинального алгоритма Форда-Белл- мана.
В рамках данной статьи для планирования совместных действий объектов СТС предложено развивать подходы, основанные на использовании графовых моделей и алгоритмических средств.
Подходы к моделированию СТС для решения практических задач
Для моделирования СТС предполагается использование графовой модели и ряда алгоритмов. Рассмотрим предложенные подходы на примере решения задачи обеспечения безопасности системы охраны протяженного периметра (далее – система). Предлагается последовательность следующих действий.
1. Разработка графовой модели.
В работах [1, 2] обосновано использование в качестве модели системы охраны GH-графа, который позволяет представить разнотипные объекты, а также возможные разнотипные и сложные отношения в системе.
Объектами системы являются: наземные объекты охраны, включая стационарные объекты (здания и др.) и мобильные (транспорт, люди, роботы); потенциальные нарушители охраняемого периметра, в том числе люди, наземные роботизированные платформы; квад- рокоптеры или беспилотные летательные аппараты (БПЛА); ЛПР – лицо, принимающее решение, в качестве которого используется главный компьютер или вычислительная система, предназначенные для приема и обработки информации о состоянии объектов охра- ны, квадрокоптеров и возможных действиях нарушителей территории.
 В GH-графе для представления объектов системы используются разнотипные вершины, а для представления отношений между объек- тами системы – разнотипные и множественные связи между вершинами. В работе [1] рассмотрен пример модели на основе GH-графа, который задает часть реальной системы. В рамках данного исследования продемонстрирован пример представления на GH-графе отдельных возможных отношений в системе (рис. 1).
В GH-графе для представления объектов системы используются разнотипные вершины, а для представления отношений между объек- тами системы – разнотипные и множественные связи между вершинами. В работе [1] рассмотрен пример модели на основе GH-графа, который задает часть реальной системы. В рамках данного исследования продемонстрирован пример представления на GH-графе отдельных возможных отношений в системе (рис. 1).
На рисунке 1а ребро ge1 типа tp1 представляет отношение «удаленность объектов охраны», вес ребра µ1 = 0,3 соответствует степени удаленности объектов (низкий уровень). Объекты охраны представлены в GH-графе вершинами gv1, gv2 типа tpv1 с весами h1 = h2 = 0,3, что соответствует низкому уровню значимости объектов системы.
На рисунке 1б вершина gv8 типа tpv3 с весом h8 = 0,5 представляет квадрокоптер, а ее вес соответствует среднему уровню значимости. Дуга ge9 типа tp2 соответствует отношению «наблюдать», а вес дуги µ9 = 0,5 – степени удаленности квадрокоптера и объекта охраны (средний уровень).
На рисунке 1в отношение «удаленность объектов охраны» задано ребром ge3 типа tp1 GH-графа. Вершина gv7 типа tpv2 с весом h7 = 0,8 представляет потенциального наруши- теля, а ее вес соответствует высокому уровню значимости.
В GH-графе множественная связь в виде вектора`v1 – ребро ge19 с весами µ19.1 = 1, µ19.2 = 0, µ19.3 = 0 (рис. 1г) соответствует отношению «передача информации по каналам», в качестве каналов используются v1.1 – Wi-fi, v1.2 – Blue- tooth, v1.3 – УКВ. При этом передача информа- ции в системе происходит между квадрокоптером и ЛПР (соответственно вершины графа gv8 и gv10). Вес вершины gv10 (h10 = 1,0) соответствует высокому уровню значимости объекта. Применение множественных связей в виде вектора в GH-графе позволяет уменьшить время вычисления расстояний между вершинами не менее, чем в 1,2 раза, в зависимости от размера модели (в работе [13] проведено сравнение моделей одинаковой размерности (от 100 до 1 000 вершин) на основе GH-графа и графов, допускающих использование только разнотипных или однотипных связей).
На рисунке 1д дуга ge17 типа tp3 GH-графа представляет отношение «управлять движением квадрокоптера», а вес дуги µ17 = 1,0 – степень соответствия заданному направлению движения (максимальное значение).
Таким образом, на рассмотренных примерах можно сделать вывод об эффективности применения GH-графа для моделирования СТС, математический аппарат которого позволяет задать возможные отношения в системе и уменьшить время анализа системы с разнотипными информационными потоками.
После представления системы в виде GH-графа для решения задачи формирования зон влияния объектов системы (в данном случае – квадрокоптеров) необходимо применить один за другим два алгоритма: алгоритм пропорционального разделения GH-графа и модифицированный алгоритм Форда-Беллмана поиска кратчайших путей GH-графа. Особенностью применения данных алгоритмов является предварительная подготовка графовой модели, которая заключается в возможности фильтрации вершин и связей GH-графа по типам, что соответствует критериям использования алгоритмов.
2. Использование алгоритма пропорционального разделения GH-графа.
В работе [1] подробно рассмотрен сам алгоритм пропорционального разделения GH-графа и показано его применение для решения практической задачи формирования зон влияния объектов системы. Используя на начальном этапе в данном алгоритме критерии вы- бора типов вершин и связей, можно оставить вершины типов tpv1 и tpv2, что соответствует объектам охраны и потенциальным нарушителям системы, и связи между такими вершинами, представляющие отношения «удаленность объектов», веса которых соответствуют степени удаленности объектов охраны и/или потенциальных нарушителей системы.
Полученная таким образом графовая модель фактически представляет собой карту, на которой отмечены объекты охраны, потенциальные нарушители и расстояния между ними. Теперь такой граф в результате применения данного алгоритма делится на k частей (подграфов), где k – количество квадрокоптеров.
3. Использование модифицированного алгоритма Форда–Беллмана поиска кратчайших путей GH-графа и вычисление метрических характеристик графа.
Данный модифицированный алгоритм применяется к каждому полученному подграфу поиска кратчайших путей GH-графа, в результате чего формируются k матриц расстояний между вершинами. На основе полученных матриц вычисляются метрические характеристики подграфов. После этого выполняется сравнение на соответствие метрик подграфов и технических характеристик квадрокоптеров, в результате чего принимается решение о формировании или неформировании зон влияния объектов. Если хотя бы одна зона влияния объекта не может быть сформирована, принимается решение о повторном применении обоих алгоритмов с измененным значением k.
Рассмотрим подробнее предлагаемый в работе алгоритм.
Данный алгоритм предназначен для формирования матрицы расстояний GH-графа. Модификация алгоритма заключается в возможности поиска расстояний для полных или усеченных множеств вершин и/или связей графа, например, для связей заданного типа. Это составляет научную новизну модифицированного алгоритма и позволяет выполнить анализ разнотипных информационных потоков в СТС. Вычислительная сложность модифицированного алгоритма оценивается величиной O(n × m), как и исходного алгоритма Форда–Беллмана. Однако при этом снижается время работы алгоритма GH-графа за счет использования множественных связей в виде вектора, объединяющего ряд разнотипных связей [13].
Критерием вычисления кратчайших путей графа является учет полного или усеченного множества связей и вершин в соответствии с требованиями практической задачи.
Модифицированный алгоритм Форда–Беллмана поиска кратчайших путей GH-графа основан на следующих формальных соотношениях.
1. Формально GH-граф
G = (Gv, Ge) (1)
задается нечеткими конечными множествами вершин Gv = {gvi | i = 1, 2, …, n} (gv – graph vertex) и связей Ge = {gel | l = 1, 2, …, m}, соединяющих пары вершин (ge–graph edge) [14, 15].
Множество вершин графа содержит подмножества вершин по типу Gv = {Gv(tpvp)}.
Множество связей графа содержит подмножества однотипных связей Ge(o), разнотипных связей Ge(tpk) и связей в виде вектора Ge(ve), позволяющих объединить несколько разнотипных связей: Ge = {Ge(o), Ge(tpk), Ge(ve)}.
2. Форма представления множественных и разнотипных связей GH-графа в виде списка Le (G):
Le (G) = Cons ( : , [ige]). (2)
Здесь в качестве головы списка выступает вершина , от которой идет связь. Хвост списка – вершина , к которой идет связь от вершины , и инцидентная им связь [ige]. Все элементы списка содержат свои атрибуты. Атрибутами вершины Av = являются тип tv и вес h, а атрибутами связи – Ae = , где Por – признак ориентации; Pt – признак типа; Pv – признак вектора; μ – вес связи.
Признак ориентации Por:
Por = 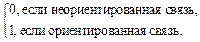 (3)
(3)
Признак типа Pt:
Pt = 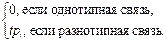 (4)
(4)
Признак вектора Pv:
Pv = 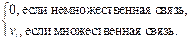 (5)
(5)
3. Определение критерия 1 поиска кратчайших путей в графе Kv(G):
 (6)
(6)
4. Определение критерия 2 поиска кратчайших путей в графе: Ke(G) = 0, если учитывается полное множество связей графа Ge.
В случае усеченного множества связей графа критерий Ke(G) вычисляется как
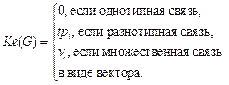 (7)
(7)
5. Используется функция GetOrAlg, реализующая выполнение оригинального алгоритма Форда–Беллмана [3, 4].
6. В результате работы модифицированного алгоритма Форда–Беллмана поиска кратчайших путей GH-графа формируется матрица расстояний в зависимости от выбранных критериев: Ad(G) = {d(gvi, gvj)}, где i, j = 1, 2, ..., (n – 1).
 На рисунке 2 приведена блок-схема модифицированного алгоритма Форда–Беллмана поиска кратчайших путей GH-графа с учетом соотношений (1)–(7).
На рисунке 2 приведена блок-схема модифицированного алгоритма Форда–Беллмана поиска кратчайших путей GH-графа с учетом соотношений (1)–(7).
Опишем алгоритм по шагам.
Шаг 1. Загрузка исходного графа G, представленного в виде списка ребер Le(G).
Шаг 2. Формирование множества вершин и связей графов Gv и Ge и значения переменной n.
Шаг 3. Ввод пользователем значения Kv(G) (см. (6)).
Шаг 4. Проверка на определение критерия 1 поиска кратчайших путей в графе. Если Kv(G) = 0, то выполняется переход к шагу 6 для определения критерия 2, иначе – переход к шагу 5.
Шаг 5. Если Kv(G) = {tpvi}, то в списке ребер и во множестве вершин исходного графа остаются только вершины заданного типа tpvi: Gv = {Gv(tpvi)}, Le(G) = Le(Gv, Ge). Формируется новое значение переменной n = | Gv |. Затем выполняется переход к шагу 6.
Шаг 6. Определение критерия 2 поиска кратчайших путей в графе путем ввода значения Ke(G) (см. (7)).
Шаг 7. Если Ke(G) = 0, то учет полного множества связей графа Ge. Иначе – переход к шагам 8–10.
Шаги 8–10. В случае усеченного множества связей графа определение критерия Ke(G) по формуле (7), таким образом, в списке остаются только связи выбранного подмножества связей, например, только однотипные связи Ge(oj), или связи выбранного типа Ge(tpj), или связи в виде заданного вектора конкретного индекса Ge(vj).
Шаги 11–14. Выполнение функции GetOrAlg, реализующей оригинальный алгоритм Форда–Беллмана.
Шаг 15. Вывод матрицы расстояний GH-гра- фа Ad(G) в зависимости от выбранных критериев 1 и 2.
Таким образом, предложенный алгоритм обладает элементами научной новизны, сохраняет вычислительную сложность исходного алгоритма Форда–Беллмана и позволяет снизить время вычислений.
Формирование зон влияния объектов системы при помощи алгоритмов
Продемонстрируем предложенный поход к решению задачи формирования зоны влияния квадрокоптера K1. Примем, что в наличии имеются модели с учетом их технических характеристик, приведенных в таблице.
Характеристики квадрокоптеров
Characteristics of the quadcopter
|
Модель квадрокоптера
|
Диаметр обзора (км)
|
Время работы аккумулятора (мин.)
|
|
DJI Matrice 300 RTK
|
0,5
|
55
|
|
DJI Mavic 2 Enterprise Advanced
|
0,95
|
150
|
|
DJI Mavic 3 Cine Premium Combo
|
0,4
|
46
|
Поскольку GH-модель является нечетким графом, переведем диаметры из км в условные единицы (1 км = 1 ед.), то есть полагаем, что 1 км – максимальная степень удаленности объектов в рассматриваемой системе.
Требуется определить наиболее подходящую модель квадрокоптера для обеспечения функций охраны участка периметра. Для этого исходную графовую модель [1] представим с учетом соотношений (6) и (7) Kv(G) = {tpv1, tpv2}, Ke(G) = {tp1}, как показано на рисунке 3. Тогда в списке Le (G) (соотношение (2)) остаются вершины и связи выбранного типа.


 Полученный граф разделим на подграфы при помощи алгоритма пропорционального разделения GH-графа с учетом выбранных критериев 1 и 2 (соотношения (6) и (7)). Полученный подграф G1 изображен на рисунке 4. На рисунке 4а вершины подграфа gv1–gv3 типа tpv1 с весами hi = 0,3 представляют объекты охраны ОО1–ОО3, а вершина gv7 типа tpv2 с весом hi = 0,8 – потенциального нарушителя ПН1. Степень удаленности объектов характеризуется весами ребер ge1–ge5 типа tp1 (µ1 = 0,3, µ2 = 0,5, µ3 = 0,4, µ4 = 0,7, µ5 = 0,6).
Полученный граф разделим на подграфы при помощи алгоритма пропорционального разделения GH-графа с учетом выбранных критериев 1 и 2 (соотношения (6) и (7)). Полученный подграф G1 изображен на рисунке 4. На рисунке 4а вершины подграфа gv1–gv3 типа tpv1 с весами hi = 0,3 представляют объекты охраны ОО1–ОО3, а вершина gv7 типа tpv2 с весом hi = 0,8 – потенциального нарушителя ПН1. Степень удаленности объектов характеризуется весами ребер ge1–ge5 типа tp1 (µ1 = 0,3, µ2 = 0,5, µ3 = 0,4, µ4 = 0,7, µ5 = 0,6).
Используя предложенный модифицированный алгоритм Форда–Беллмана поиска кратчайших путей GH-графа, для подграфа G1 сформи- руем матрицу расстояний Ad(G1). Затем с помощью стандартных средств вычисления [16] определим метрические характеристики подграфа – радиус r(G1) = 0,5 и диаметр d(G1) = 0,7.
С учетом характеристик квадрокоптеров для обеспечения функций охраны участка периметра подходит только модель DJI Mavic 2 Enterprise Advanced с максимальным диаметром обзора 0,95. На подграфе такой квадрокоптер K1 может быть представлен вершиной gv8 типа tpv3 с весом h8 = 0,5, как показано на рисунке 4б. Здесь все дуги ge9–ge12 типа tp2 (отношение «наблюдать») с соответствующими весами.
Таким образом, предложенный подход, основанный на применении GH-графа и двух алгоритмов (алгоритма пропорционального разделения графа и модифицированного алгоритма Форда–Беллмана), позволяет уменьшить время анализа разнотипных данных в СТС и может быть использован в общем случае для решения задачи классификации на графах, пример которой рассмотрен на задаче формирования зон влияния объектов системы.
Программная реализация
Структура программного комплекса, позволяющего реализовать модели на основе GH-графов, представлена и подробно описана в [1]. Разработанные в рамках данного исследования алгоритмические средства составляют блок вычисления характеристик GH-графа в программном комплексе [17]. Обновление предложенного ранее программного комплекса заключается в модификации графовой модели и алгоритмов за счет допустимости разнотипных вершин. Структура блока вычисления характеристик обновленного программного комплекса моделирования системы на основе GH-графа изображена на рисунке 5.
Здесь модуль ввода/вывода данных служит для организации ввода исходного графа G, представленного в виде списка ребер Le(G), и вывода численных значений характеристик графа, в том числе радиуса, диаметра, подмножества центральных и периферийных вершин и др. Для хранения входных, выходных данных и промежуточных результатов работы блока служит модуль хранения. В качестве промежуточных результатов данный модуль позволяет сохранить таблицу расстояний и эксцентриситеты вершин графа.
Последовательность вычисления характеристик GH-графа:
– реализация модифицированного алгоритма Форда–Беллмана поиска кратчайших путей GH-графа, в результате чего формируется таблица расстояний;
– на основании полученной таблицы расстояний вычисление численных значений эксцентриситетов вершин графа;
– в зависимости от полученных значений эксцентриситетов вершин вычисление метрических характеристик и определение подмножеств центральных и периферийных вершин графа.
Для реализации программного комплекса использован язык программирования C++ (включая библиотеку Qt). Комплекс может функционировать в различных операционных системах, и планируется его использование с применением SQL или NoSQL БД, например, графовой СУБД Neo4j и т.д. [18].
Заключение
В статье описан подход моделирования СТС, основанный на использовании GH-графа и двух алгоритмов (алгоритма пропорционального разделения графа и модифицированного алгоритма Форда–Беллмана) и позволяющий выполнять анализ разнотипных данных. Предложен модифицированный алгоритм поиска кратчайших путей Форда–Беллмана, приведены блок-схема алгоритма и его пошаговое описание. Показаны преимущества предложенного подхода, заключающиеся в следующем: вычислительная сложность модифицированного алгоритма не отличается от сложностиисходного алгоритма Форда–Беллмана; время анализа разнотипных данных СТС снижается за счет использования множественных связей в виде вектора в GH-графе.
Для GH-модели, разработанной ранее, рассмотрены возможности применения алгоритмов для решения задачи формирования зон влияния объектов в системе на примере системы охраны протяженного периметра. Показаны возможности использования предложенного подхода для решения данной задачи, в том числе выбор конкретной модели квадрокоптера подсистемы и определение количества квадрокоптеров с заданными техническими характеристиками, необходимые для организации видеонаблюдения системы охраны. Использование предложенных алгоритмов на GH-графе позволяет решить задачу классификации, что продемонстрировано на рассмотренном примере. Реализованы блок вычисления характеристик графа в ПК, а также соответствующее ПО для поддержки предложенного подхода на основе графовой модели.
Список литературы
1. Мунтян Е.Р. Разработка алгоритма пропорционального разделения GH-графа для формирования зон влияния объектов в сложных технических системах // Программные продукты и системы. 2023. Т. 36. № 3. С. 378–387. doi: 10.15827/0236-235X.143.378-387.
2. Еремеев А.П., Мунтян Е.Р. Разработка онтологии на основе графов с множественными и разнотипными связями // Искусственный интеллект и принятие решений. 2021. № 3. С. 3–18. doi: 10.14357/20718594210301.
3. Сысоев В.В. Итерационный алгоритм поиска кратчайшего пути в невзвешенном неориентированном графе // Современные информационные технологии и ИТ-образование. 2021. Т. 17. № 3. С. 585–592.
4. Близнякова Е.А., Куликов А.А., Куликов А.В. Сравнительный анализ методов поиска кратчайшего пути в графе // Архитектура, строительство, транспорт. 2022. № 1. С. 80–87. doi: 10.31660/2782-232X-2022-1-80-87.
5. Хренов В.В. Модификации алгоритма Дейкстры для поиска кратчайшего пути // АИ. 2023. № 13. С. 12–17.
6. Cormen Th.H., Leiserson Ch.E., Rives R.L., Stein C. Introduction to Algorithms. MIT Press and McGraw-Hill Publ., 2022, 1312 p.
7. Bellman R. On a routing problem. Quart. Appl. Math., 1958, vol. 16, pp. 87–90. doi: 10.1090/QAM/102435.
8. Ford L.R., Fulkerson D.R. Flows in Networks. Princeton University Press, 1962, 216 p.
9. Смирнов А.В. Задача о кратчайшем пути в кратном графе // Моделирование и анализ информационных систем. 2017. Т. 24. № 6. С. 788–801. doi: 10.18255/1818-1015-2017-6-788-801.
10. Zhang J., Li W., Yuan L., Qin L., Zhang Y., Chang L. Shortest-path queries on complex networks: Experiments, analyses, and improvement. PVLDB, 2022, vol. 15, no. 11, pp. 2640–2652. doi: 10.14778/3551793.3551820.
11. Ураков А.Р., Тимиряев Т.В. Алгоритм решения динамической задачи поиска кратчайших расстояний в графе // Управление большими системами. 2017. № 65. С. 60–86.
12. Агафонов А.А., Мясников В.В. Метод определения надежного кратчайшего пути в стохастической сети с использованием параметрически заданных устойчивых распределений вероятностей // Тр. СПИИРАН. 2019. Т. 3. № 18. С. 558–582. doi: 10.15622/sp.2019.18.3.557-581.
13. Мунтян Е.Р. Реализация нечеткой модели взаимодействия объектов сложных технических систем на основе графов // Программные продукты и системы. 2019. Т. 32. № 3. С. 411–418. doi: 10.15827/0236-235X.127.411-418.
14. Minaev Y.N., Filimonova O.Y., Minaeva J.I., Filimonov A. Fuzzy mathematics with limited possibilities for assigning membership functions. Cybernetics and Systems Analysis, 2020, vol. 56, рр. 29–39. doi: 10.1007/s10559-020-00218-9.
15. Дандыбаев С.Т. Нечеткие множества с нечеткими функциями принадлежности // Теория и практика современной науки. 2021. № 1. С. 130–133.
16. Muntyan E.R., Melnik E.V. The graph-based analysis of structural delays in distributed multiprogram systems of information processing. JPCS, 2020, vol. 1661, no. 1, art. 012061. doi: 10.1088/1742-6596/1661/1/012061.
17. Мунтян Е.Р. Программный модуль для моделирования взаимодействия акторов и групп акторов на основе графов: Свид. о регистр. ПрЭВМ № 2018665593. Рос. Федерация, 2018.
18. Еремеев А.П., Панявин Н.А. Унификация модели представления данных и преобразование форматов на основе нереляционной СУБД Neo4j // Программные продукты и системы. 2022. Т. 35. № 4. С. 549–556. doi: 10.15827/0236-235X.140.549-556.
References
1. Muntyan, E.R. (2023) ‘Developing a GH-graph proportional separation algorithm to form of object influence zones in complex technical systems’, Software & Systems, 36(3), pp. 378–387 (in Russ.). doi: 10.15827/0236-235X.143.378-387.
2. Eremeev, A.P., Muntyan, E.R. (2021) ‘Development of an ontology based on graphs with multiple and different types of edges’, Artificial Intelligence and Decision Making, (3), pp. 3–18 (in Russ.). doi: 10.14357/20718594210301.
3. Sysoev, V.V. (2021) ‘Iterative algorithm for finding the shortest ways in an unweighted undirected graph’, Modern Information Technologies and IT-Education, 17(3), pp. 585–592 (in Russ.).
4. Bliznyakova, E.A., Kulikov, A.A., Kulikov, A.V. (2022) ‘Comparative analysis of methods for finding the shortest distance in a graph’, Architecture, Construction, Transport, (1), pp. 80-87 (in Russ.). doi: 10.31660/2782-232X-2022-1-80-87.
5. Khrenov, V.V. (2023) ‘Modifications of the Dijkstra algorithm for finding the shortest path’, Actual Research, (13), pp. 12–17 (in Russ.).
6. Cormen, Th.H., Leiserson, Ch.E., Rives, R.L., Stein, C. (2022) Introduction to Algorithms. MIT Press and McGraw-Hill Publ., 1312 p.
7. Bellman, R. (1958) ‘On a routing problem’, Quart. Appl. Math., (16), pp. 87–90. doi: 10.1090/QAM/102435.
8. Ford, L.R., Fulkerson, D.R. (1962) Flows in Networks. Princeton University Press, 216 p.
9. Smirnov, A.V. (2017) ‘The shortest path problem for a multiple graph’, Modeling and Analysis of Information Systems, 24(6), pp. 788–801 (in Russ.). doi: 10.18255/1818-1015-2017-6-788-801.
10. Zhang, J., Li, W., Yuan, L., Qin, L., Zhang, Y., Chang, L. (2022) ‘Shortest-path queries on complex networks: Experiments, analyses, and improvement’, PVLDB, 15(11), pp. 2640–2652. doi: 10.14778/3551793.3551820.
11. Urakov, A.R., Timiryaev, T.V. (2017) ‘Algorithm for solving the dynamic problem of finding the shortest distances in a graph’, Large-Scale Systems Control, (65), pp. 60–86 (in Russ.).
12. Agafonov, A.A., Myasnikov, V.V. (2019) ‘Method for reliable shortest path determination in stochastic networks using parametrically defined stable probability distributions’, SPIIRAS Proc., 3(18), pp. 558–582 (in Russ.). doi: 10.15622/sp.2019.18.3.557-581.
13. Muntyan, E.R. (2019) ‘Implementation of a fuzzy model of interaction between objects in complex technical sys-tems based on graphs’, Software & Systems, 32(3), pp. 411–418 (in Russ.). doi: 10.15827/0236-235X.127.411-418.
14. Minaev, Y.N., Filimonova, O.Y., Minaeva, J.I., Filimonov, A. (2020) ‘Fuzzy mathematics with limited possibilities for assigning membership functions’, Cybernetics and Systems Analysis, 56, рр. 29–39. doi: 10.1007/s10559-020- 00218-9.
15. Dandybaev, S.T. (2021) ‘Fuzzy sets with fuzzy membership functions’, Theory and Practice of Modern Sci., (1), pp. 130–133 (in Russ.).
16. Muntyan, E.R., Melnik, E.V. (2020) ‘The graph-based analysis of structural delays in distributed multiprogram systems of information processing’, JPCS, 1661(1), art. 012061. doi: 10.1088/1742-6596/1661/1/012061.
17. Muntyan, E.R. (2018) A Software Module for Modeling the Interaction of Actors and Actors Groups Based on Graphs. Pat. RF, № 2018665593.
18. Eremeev, A.P., Paniavin, N.A. (2022) ‘Unification of a data presentation model and format conversion based on a non-relational Neo4j DBMS’, Software & Systems, 35(4), pp. 549–556 (in Russ.). doi: 10.15827/0236-235X.140.549-556.


 (6)
(6)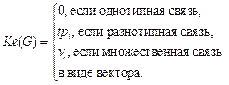 (7)
(7)


