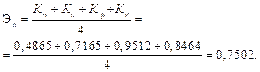Программные продукты и системы

Введение. Неизбежное усложнение систем, и в первую очередь искусственных организационно-технических, создаваемых человеком в разных областях деятельности, обусловило необходимость предвидеть результаты длительных и дорогостоящих работ по их созданию и поиску инструментария для этого [1]. Цель поиска – увидеть и оценить функционирование создаваемой системы раньше, чем она будет создана физически [2].

Общая методология функционального моделирования IDEF включает в себя ряд частных методологий. Одна из них, IDEF0, используется для создания функциональных моделей, отображающих структуру и функции системы, а также потоки информации и материальных объектов, преобразуемые этими функциями.  С помощью наглядного графического языка IDEF0 изучаемая система предстает перед разработчиками и аналитиками в виде набора  взаимосвязанных функций (в терминах IDEF0 – функциональных блоков).

Известно, что любая система создается для того, чтобы функционировать. Результатом работы системы является осуществление ею материально-информационных обменов, то есть преобразований ее входов в выходы [3]. Система обеспечивается материальной инфраструктурой, составляющей ее устройство и морфологию. Характер (режим) функционирования системы в пределах ее морфологических возможностей определяется управлением работой системы. Именно особенности функционирования обусловливают и морфологию, и ма- териально-информационные потоки системы [4].

Функциональная модель есть графическое представление функционирования систем и объектов [5]. Она может использоваться как для анализа процессов, протекающих в существующих системах (их функционирование), так и при проектировании новых систем для синтеза их структур [6]. Однако анализ функциональных моделей в настоящее время выполняется на качественном уровне путем анализа структуры связей между отдельными функциями моделируемого процесса, а также сравнения различных структур процесса и раз- личных процессов между собой. В незначительном количестве имеющихся источников и документов по методологии функционального моделирования нет информации о методах аналитического количественного анализа функциональных моделей и процессах, описываемых ими [7–9].

Функциональная модель двух сложных взаимодействующих систем с антагонистическими целями представляет собой противоборство двух сложных, например, конкурирующих систем. В общем случае такой процесс может содержать в себе два варианта процессов: с одной стороны – воздействие, атака на систему, с другой – защита от воздействия  и противодействие, а также одновременно воздействие и защита от него каждой сложной системой.

В первом случае процесс будет иметь один выход – из атакуемой системы, во втором два – из каждой системы. В статье рассматривается только первый вариант, поскольку второй является частным случаем и принципиально не отличается от первого.

Процесс действий двух сложных систем  с антагонистическими целями в нотации технологии IDEF0 представлен на рисунке. Он включает в себя шесть процедурных функций (А1–А3, Б1–Б3), выполняющих, скажем, обработку информации, и две специфические функции управления процессом (А0, Б0), связанные между собой прямыми и обратными функциональными связями. Процесс имеет один вход из внешней среды (может быть из другого процесса – Out1) и один выход во внешнюю среду (во внешние процессы – In1). Как видно, вход из внешней среды выполняется через функ- цию А1, обеспечивающую обработку входной информации и ее передачу другим функциям. Выход во внешнюю среду осуществляется функцией Б3, которая, очевидно, решает основные задачи процесса, а остальные – обеспечивающие. Следует заметить, что количество входов и выходов в общем случае может быть любым и определяется только структурой исследуемого процесса [10].

Интерпретируя функциональную модель как орграф, сформируем матрицу связей функций моделируемого процесса, представленную в таблице. В матрице по строкам единицами и нулями записаны входы в функции, по столбцам, соответственно, – выходы из них. Суммы входов по строкам и выходов по столбцам позволяют ранжировать функции по степени важности в исследуемом процессе. Общая сумма входов и выходов позволяет сравнивать структуры одного процесса и разные процессы по их сложности [10].

Матрица связей функциональной модели двух сложных взаимодействующих систем  с антагонистическими целями

Relationship matrix for a functional model  of two complex interacting systems  with antagonistic goals

Эффективность процесса может быть определена как среднее арифметическое четырех коэффициентов и рассчитывается по формуле

                         (1)

Км – масштабный коэффициент процесса, оценивающий количество функций в нем. Чем больше коэффициент, тем сложнее процесс. Расчет осуществляется по формуле

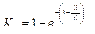                                      (2)

где fΣ – общее количество функций исследуемого процесса.

Кс – коэффициент связанности функций процесса, оценивающий коммуникативность функций в процессе. Более сложный процесс имеет больший коэффициент связанности. Расчет осуществляется по формуле

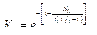                                     (3)

где SΣ – общее число связей, то есть число единиц в матрице.

Кр – коэффициент равномерности распределения функций в процессе. Чем меньше коэффициент равномерности, тем лучше структурирован процесс. Коэффициент рассчитывается по формуле

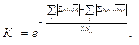                           (4)

где Σin – сумма единиц в строке, то есть сумма входных связей функции процесса; 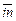 – среднее число входных связей; Σout – сумма единиц в столбце, то есть сумма выходных связей функции процесса;  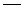– сумма единиц в столбце, то есть среднее число выходных связей.

Ки – коэффициент изолированности функций, определяющий общее число несвязанных функций, а также не имеющих входов или выходов. Изолированные функции не влияют на качество процесса и рассчитываются по формуле

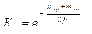                                       (5)

где пстр – число пустых строк (число функций без входов); псто – число пустых столбцов (функций без выходов).

Числовые значения матрицы связей функциональной модели действий двух сложных взаимодействующих систем с антагонистическими целями из рассматриваемого примера подставим в формулы (1)–(5) и произведем расчет коэффициентов и эффективности процесса.

Масштабный коэффициент процесса.

Общее количество функций fΣ = 6, тогда

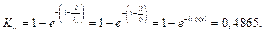
Коэффициент связанности функций процесса.

Общее число связей, то есть число единиц  в матрице SΣ = 20, тогда

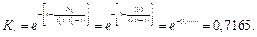
Коэффициент равномерности распределения функций в процессе.

Среднее число входных связей 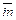 = 10.

Среднее число выходных связей 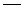 = 12.

Коэффициент изолированности функций.

Число пустых строк пстр = 0, число пустых столбцов псто = 2, тогда

Эффективность процесса.

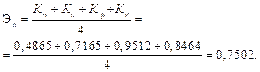
Таким образом, получена оценка эффективности функциональной модели при воздействии на нее другой системы.

Заключение

В статье сделан общий анализ функционального моделирования двух сложных взаимодействующих систем с антагонистическими целями. Выполнен расчет эффективности действий функциональной модели двух этих систем.

Предлагаемый метод позволяет оценить эффективность сложной системы при преднамеренном или непреднамеренном воздействии  на функции исследуемой системы другой системы, имеющей, как правило, противоположные, антагонистические, цели.

Список литературы

1. Харари Ф. Теория графов. М.: Книжный дом «ЛИБРОКОМ», 2009. 300 с.

2. Ильин В.А., Козлов И.Л. К проблеме автоматизации управления силами и средствами, функциональное моделирование // Автоматизация процессов управления. 2009. № 4. С. 53–57.

3. Дубейковский В.И. Практика функционального моделирования с AllFusion Process Modeler. М.: Диалог-МИФИ, 2004. 364 с.

4. Шпак В.Ф., Директоров Н.Ф. и др. Информационные технологии в системе управления силами ВМФ. СПб: Элмор, 2005. 827 с.

5. Дрешер Д. Основы блокчейна: вводный курс для начинающих в 25 небольших главах. М.: ДМК Пресс, 2018. 320 с.

6. Карпычев В.Ю. Функциональное моделирование (IDEF0) как метод исследования блокчейн-технологии // Тр. НГТУ им. Р.Е. Алексеева. 2018. № 4. С. 22–32.

7. Тебекин А.В. Методология функционального моделирования сложных технических систем модульного типа // Журнал технических исследований. 2021. Т. 7. № 2. С. 3–12.

8. Тебекин А.В., Тебекин П.А., Егорова А.А. Технологические трансформации XXI века как индуцирующий вектор перехода к новому качеству производства // Теоретическая экономика. 2021. № 1. С. 42–53.

9. Тебекин А.В., Петров В.С. Использование методологии моделирования IDEF при формировании структурно-параметрической модели реализации технологий обеспечения эффективного развития промышленных предприятий в условиях постиндустриальной экономики // Транспортное дело России. 2017. № 4. С. 43–49.

10. Ильин В.А., Янча С.П. Методы анализа функциональных моделей // Программные продукты и системы. 2009. Т. 22. № 4. С. 32–34.

References

1. Harari, F. (1969) Graph Theory. Addison-Wesley Publ., 274 p. (Russ. ed.: (2009) Moscow, 300 p.).

2. Ilin, V.A., Kozlov, I.L. (2009) ‘On the problem of automation of control of forces and means, functional modeling’, Automation of Control Processes, (4), pp. 53–57 (in Russ.).

3. Dubeykovskiy, V.I. (2004) Practice Functional Modeling with AllFusion Process Modeler. Moscow, 364 p. (in Russ.).

4. Shpak, V.F., Direktorov, N.F. (2005) Information Technologies in the Navy Force Management System. St. Petersburg, 827 p. (in Russ.).

5. Drescher, D. (2017) Blockchain Basics: A Non-technical Introduction in 25 Steps. 255 p. (Russ. ed.: (2018) Moscow, 320 p.).

6. Karpychev, V.Y. (2018) ‘Functional modeling (IDEF0) as a method of research on blockchain technology’, Transactions of NNSTU n.a. R.Е. Alekseev, (4), pp. 22–32 (in Russ.).

7. Tebekin, A.V. (2021) ‘Methodology for functional modeling of complex technical systems of modular type’, J. of Tech. Research, 7(2), pp. 3–12 (in Russ.).

8. Tebekin, A.V., Tebekin, P.A., Egorova, A.A. (2021) ‘Technological transformations of the 21st century as an indu-cing vector of transition to a new quality of production’, Theoretical Economics, (1), pp. 42–53 (in Russ.).

9. Tebekin, A.V., Petrov, V.S. (2017) ‘Using the modeling methodology IDEF in the formation of structural-parametric model for the implementation of technology ensure the efficient development of industrial enterprises in the condition of postindustrial economy’, Transport Business of Russia, (4), pp. 43–49 (in Russ.).

10. Ilin, V.A., Yancha, S.P. (2009) ‘Methods analisis of functional models’, Software & Systems, 22(4), pp. 32–34 (in Russ.).