Введение. Генераторы случайных и псевдослучайных чисел являются одной из ключевых компонент информационных систем для разнообразных сфер деятельности. Случайные числа используются в криптографических приложениях для создания шифров и ключей безопасности, в финансовых моделях для симуляции рыночных колебаний и прогнозирования инвестиций, в научных исследованиях при моделировании случайных процессов, в статистическом анализе и, конечно, в разнообразных  игровых и развлекательных приложениях. Сегодня существует множество алгоритмов и техник для получения случайных и псевдослучайных чисел, поэтому разработчик приложения неизбежно столкнется с задачей оценки качества работы того или иного генератора для принятия решения о пригодности его использования.

Существуют два основных типа генераторов случайных последовательностей: генераторы случайных чисел (ГСЧ, англ. RNG) и генераторы псевдослучайных чисел (ГПСЧ, англ. PRNG). Оба типа создают набор нулей и единиц, которые затем могут быть разделены на блоки чисел требуемых длины и типа.

Генератор истинно случайных нулей и единиц можно представить как абстрактный механизм для подбрасывания идеальной монетки со сторонами, помеченными 0 и 1. Если принять  в расчет, что броски не зависят друг от друга, вероятность получения 0 или 1 будет равна  50 %. Главное преимущество такого идеального генератора в том, что значение следующего элемента последовательности невозможно предсказать. На практике ГСЧ для  создания случайности использует источник энтропии, обрабатываемый при помощи некоторой функции. Этот процесс, известный как дистилляция энтропии, позволяет нивелировать слабости источника, которые могут приводить к появлению чрезмерно длинных или повторя- ющихся последовательностей нулей и единиц. В качестве источника энтропии современные ГСЧ могут использовать, например, шу- мы токов в электрической цепи (https://www. researchgate.net/publication/306370204_Intel's_digital_random_number_generator_DRNG), движения курсора мыши по экрану или белый шум звукового кодека.

ГПСЧ использует одно или несколько входных данных – так называемых зерен (англ. seed), которые в идеальном случае должны быть случайными и непредсказуемыми. Можно сказать, что для получения максимально качественного результата генерации ГПСЧ должен получать начальные значения из выходных данных ГСЧ, то есть от источника энтропии. Выходные данные ГПСЧ обычно являются детерминированными функциями начального значения, из-за чего при описании таких генераторов и применяется термин «псевдослучайный». Важная особенность всех ГПСЧ – повторяемость. Это значит, что каждый элемент псевдослучайной последовательности можно воспроизвести из начального числа. Свойство повторяемости позволяет выполнять проверку генерации или генерировать общий набор данных для отдельных клиентов приложения.

Ключевой характеристикой генераторов, пригодных для использования в криптографических приложениях, является непредсказуемость. ГПСЧ обладают свойствами прямой и обратной непредсказуемости. Прямая непредсказуемость – это невозможность предсказать следующее выходное число данной последовательности (даже если известны все предыдущие числа), если зерно остается неизвестным. Обратная непредсказуемость – это невозможность определить зерно на основе знания о любых сгенерированных значениях. Для качественного ГПСЧ не должна быть очевидной никакая корреляция между зерном и любым числом, сгенерированным с использованием этого зерна. То есть каждый элемент последовательности должен казаться результатом независимого случайного события. Однако если зерно и алгоритм генерации станут известны, тогда все генерируемые значения можно предсказать и случайность исчезнет. Математические алгоритмы большинства современных ГПСЧ общеизвестны (например, вихрь Мерсенна), поэтому для получения непредсказуемых последовательностей крайне важно хранить начальное значение в секрете или изменять его непредсказуемым образом.

Обзор существующих методов  оценки ГСЧ

Свойства любой случайной последовательности могут быть охарактеризованы и описаны с точки зрения вероятности. Существует несколько способов оценить качество ГСЧ, включая статистические тесты и оценку аппаратуры. Каждый статистический тест служит для проверки гипотезы о случайности входной последовательности. Для этого задается параметр a, обозначающий уровень значимости (то есть вероятность ложноотрицательного результата). Обычно a берется равным 0,01 или 0,001.  На основе входных данных статистический тест вычисляет так называемое P-значение – вероятность того, что идеальный ГСЧ сгенерирует последовательность менее случайную, чем проверяемая этим тестом. Если P-значение больше a, то гипотеза о случайности принимается, иначе отвергается [1]. Аппаратные тесты позволяют удостовериться, что физические приборы, используемые для генерации случайных чисел, работают правильно и не содержат уязвимостей или слабых мест, которые могут поставить под угрозу безопасность ГСЧ.

При тестировании двоичных последовательностей принимаются три предположения [2].

1.    Единообразие: в любой момент генерации последовательности появление нуля или единицы одинаково вероятно. Для генераторов, выдающих последовательности натуральных десятичных чисел, предположение о единообразии можно переформулировать так: в любой момент генерации последовательности появление любого числа из заданного диапазона одинаково вероятно.

2.    Масштабируемость: любой тест, применимый к последовательности, также может быть применен к подпоследовательностям, случайным образом извлеченным из заданной последовательности.

3.    Согласованность: генератор должен демонстрировать единообразное поведение для любых начальных значений.

Существуют две общепризнанные организации, занимающиеся разработкой стандартов, алгоритмов, протоколов и методов тестирования и оценки криптографических систем и продуктов. Это Национальный институт стандартов и технологий США (NIST) и Национальное агентство по кибербезопасности Германии (BSI). Но, помимо государственных институтов, свои программные решения и методы оценки ГСЧ также предлагают независимые организации и исследователи. Рассмотрим некоторые из наиболее популярных.

Dieharder – расширенный набор из 15 статистических тестов Джорджа Марсальи [3]. Для проведения серии тестов необходимо сформировать бинарный файл, состоящий из последовательности нулей и единиц. Программа генерирует текстовый файл отчета, в котором можно найти рассчитанные P-значения. Также в пакет входит приложение для быстрой генерации псевдослучайных последовательностей по одному из выбранных алгоритмов. Например, первый тест из пакета Dieharder называется Birthday Spacings. Его суть в следующем: выбираются m дней рождений в году, состоящем из n дней. Указываются промежутки между днями рождения. Пусть j –количество значений, которые встречаются в этом списке более одного раза. Значит, j асимптотически распределено по Пуассону  со средним значением . В тесте принято  n = 224 и m = 29. Отсюда базовое распределение j принимается пуассоновским с параметром . Берется выборка из 500 значений j,  и критерий соответствия c2 дает P-значение. Первый тест использует биты 1–24 (считая слева) целых чисел в указанном файле. Затем файл закрывается и снова открывается. Далее биты 2–25 используются для указания дней рождения. Затем берутся биты 3–26 и так далее до битов 9–32. Каждый набор битов предоставляет P-значение, а девять P-значений предоставляют выборку для проведения теста Колмогорова–Смирнова.

PractRand – набор из пяти статистических тестов: BCFN, DC6, Gap16, BRank, FPF [4]. Например, тест Gap16 используется для определения значимости интервала между повторением одной и той же цифры. Результаты Gap-16 не должны иметь существенную корреляцию  с другими стандартными тестами. Провалы  теста Gap16 при P-значениях, близких к 1, обычно свидетельствуют о том, что выходные данные ГПСЧ были слишком систематизированными, например, когда одноцикловый ГПСЧ приблизился к концу своего цикла. С другой стороны, провалы при P-значениях, близких  к 0, указывают на то, что промежутки между некоторыми числами оказались более экстремальными, чем ожидалось. Чаще всего такое поведение характерно для одноцикловых ГПСЧ и ГПСЧ типа RC4.

Тест ENT – инструмент командной строки, рассчитывает пять параметров: энтропию, хи-квадрат, среднее арифметическое, значение Монте Карло для p и коэффициент последовательной корреляции (https://www.fourmilab.ch/ random/). Тут интересно рассмотреть принцип работы теста Монте Карло для p. Каждая следующая последовательность из шести байтов преобразуется в 24-битные координаты (x, y) точки внутри квадрата. Если расстояние до точки меньше радиуса круга, вписанного в квадрат, шестибайтовая последовательность считается попаданием. Процент попаданий можно использовать для расчета значения p. Если последовательность близка к случайной, то для очень больших потоков чисел результат теста будет приближаться к истинному значению p.

RaBiGeTe MT – инструмент для оценки  качества ГПСЧ, содержащий серию из 24 статистических тестов для обнаружения систематических ошибок или закономерностей в выходных данных ГПСЧ (http://cristianopi.alter- vista.org/RaBiGeTe_MT/). Тест RaBiGeTe MT поддерживает многопоточность, имеет графический интерфейс и обладает широкими возможностями настройки параметров тестов. Входные данные представляют собой библиотеку DLL, содержащую последовательность выходных битов генератора. В качестве примера можно рассмотреть алгоритм теста коротких блоков. Тестируемая последовательность преобразуется в последовательность блоков длины S. Берется некоторое число n, после чего первый блок формируется из битов 0, n, 2n, …, (s – 1)n; второй блок формируется из битов 1,  n + 1, 2n + 1, …, (s – 1)n + 1 и т.д. Каждый блок рассматривается как число в диапазоне от 0  до 2S – 1. Распределение этих чисел сравнивается с равномерным распределением.

NIST – тестовый пакет, включающий  15 тестов [5]: частотный (монобитный) тест, проверку частоты внутри блока, тест на прогоны, тест на самую длинную серию единиц  в блоке, тест ранга двоичной матрицы, тест дискретного преобразования Фурье (спектральный тест), тест на соответствие непере- секающихся шаблонов, тест на соответствие  перекрывающихся шаблонов, универсальный статистический тест Маурера, тест линейной сложности, последовательный тест, приблизительный тест энтропии, тест кумулятивных сумм, тест на случайные отклонения и тест  на вариант случайного отклонения.

Например, в монобитном тесте внимание уделяется соотношению нулей и единиц во всей последовательности. Этот тест оценивает близость доли единиц к 0,5, то есть количество единиц и нулей в последовательности должно быть примерно одинаковым.

Применить его для тестирования натуральных десятичных чисел тоже возможно – для этого понадобится записать все десятичные числа в двоичном виде в единую строку. Нули полученной последовательности преобразуются в –1 типа int, единицы преобразуются в +1 типа int. После этого все –1 и +1 последовательно складываются:

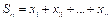                                  (1)

и полученная сумма делится на квадратный корень из общего количества слагаемых:

                                              (2)

На финальном этапе теста вычисляется хвостовая вероятность P путем применения дополняющей функции ошибок к результату предыдущей операции, деленному на корень из 2:

                                            (3)

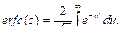                               (4)

Перечисленные тестовые системы позволяют математически точно оценить качество того или иного ГСЧ, отчего широко используются при их проектировании. Например, в [6] представлено семейство равномерных генераторов псевдослучайных чисел, основанных на обобщенных отображениях Коллатца, полученных на основе гипотезы Коллатца и последовательностей Вейля. Для тестирования генераторов автор использует тестовые пакеты NIST, Dieharder, TestU01 (Big Crush) и PractRand. Генераторы Коллатца–Вейля прошли все тесты межпотоковых корреляций, и это подтверждает, что их можно использовать для генерации множества независимых последовательностей.

Работа [7] посвящена разработке цифрового криптографически безопасного ГПЧ (CSPRNG), который включает в себя детерминированный генератор случайных битов (DRBG), отвечающий требованиям безопасности для криптографических приложений, а также источник энтро- пии, реализованный на базе кольцевого осциллятора Фибоначчи–Галуа (FiGaRO). Авторы данного источника продемонстрировали хорошую портативность и высокий уровень энтропии. Для тестирования генератора, оценки его энтропии и случайности использованы пакеты NIST и BSI.

Предлагаемое решение

Все рассмотренные методы оценки являются математическими, то есть выдают некую численную оценку для входного набора чисел (битов). При написании собственного ГСЧ или модификации существующего алгоритма на- равне с математическими методами хочется также иметь средство быстрой, но приблизительной оценки качества перемешивания, что- бы можно было на раннем этапе разработки выявлять ошибки, паттерны и повторяющиеся структуры. Человеческий глаз способен очень быстро фиксировать закономерности и повторения на изображениях, но не в наборах из нулей и единиц. Поэтому визуализация массива чисел в виде цветов палитры (красный R, зеленый G, синий B) позволит быстро фиксировать ошибки и артефакты, появляющиеся в выходных последовательностях ГСЧ (https://habr.com/ ru/companies/vk/articles/574414/).

Кодирование цвета. Положительный диапазон типа int составляет от 0 до 2 147 483 647, соответственно, для описания любого числа из этого диапазона понадобится 31 бит. Цветовая палитра TrueColor, являющаяся на сегодня стандартом представления цвета, позволяет описать 16,7 млн. значений цвета, а также 256 уровней прозрачности (альфа-канала). Каждой цветовой компоненте выделяется по 8 бит. Если же отбросить канал прозрачности, останутся 24 бита цвета. Соответственно, можно разбить любое целое 24-битное число на три байта и преобразовать его в цвета для отображения на экране. Существуют три основных типа записи цветов по каналам: десятичный – когда каждому цвету соответствуют значения от 0 до 255, нормализованный – значения от 0 до 1 и шестнадцатеричный – значения от 0 до FF. При использовании шестнадцатеричного кодирования перед числом, обозначающим итоговый цвет, ставится символ решетки.

Конкретно в C# цвет представляется в виде векторной структуры с тремя параметрами типа float. Здесь применяется нормализованный тип кодирования с диапазоном от 0.0f до 1.0f. Для разбиения целого числа на байты был написан метод GetByte, у которого первым аргументом указывается число, а вторым – желаемый байт. Представим его код:

 

int GetByte (int rn, int byte)

{   int number = ((rn >> (8 * byte)) % 256 + 256) % 256;

return number;   }

Чтобы получить нормализованное представление цвета, нужно вызвать метод GetByte три раза – для нулевого, первого и второго байтов числа, поделить выходное значение на 255 и записать результат в переменные r, g и b, из которых затем будет сформирован вектор типа Color для хранения цвета:

 

float r = GetByte(result, 0) / 255f;

float g = GetByte(result, 1) / 255f;

float b = GetByte(result, 2) / 255f;

colorToPaintPixel = new Color(r, g, b);

Полученный цвет можно использовать для закраски пикселя текстуры.

Попиксельное закрашивание. В движке Unity существует метод SetPixel класса Texture2D, который используется для закрашивания конкретного текселя текстуры в заданный цвет. Позиция текселя задается целыми числами x, y. Для облегчения текстурной разверт- ки и корректной работы мип-мэппинга в компьютерной графике принято использовать квадратные текстуры со стороной, кратной степени двойки. Текстура размером 256×256 текселей позволит визуализировать 65 536 случайных чисел, чего вполне достаточно для оценки возникновения паттернов и повторяющихся структур.

Чтобы получить визуализацию массива чисел в виде закрашенных пикселей, необходимо проделать следующие шаги:

– создать квад (Quad) – квадратную плоскую поверхность, состоящую из двух треугольников;

– применить к кваду материал типа Unlit/ Texture;

– при запуске сгенерировать новую 2D-текстуру и применить ее к материалу квада;

– установить режим фильтрации – точечная выборка, чтобы тексели не размывались по краям;

– отключить тайлинг (повторение), чтобы текстура не размывалась по границам квада.

Для модификации текстуры квада в реальном времени был написан скрипт PixelPaint.cs:

pixelTexture = new Texture2D(xMax, yMax);

GetComponent().material.mainTexture = pixelTexture;

pixelTexture.filterMode = FilterMode.Point; // Точечная выборка (без фильтрации)

pixelTexture.wrapMode = TextureWrapMode.Clamp; // Отключение тайлинга

Для тестирования визуализатора в програм- ме использованы четыре разных алгоритма ГПСЧ: метод System.Random языка C#, метод Unity Random игрового движка Unity, классическая функция Rand языков C/C++ и алгоритм Лемера.

C Rand. Стандартная функция C и C++ rand представляет собой линейный конгруэнтный генератор. Алгоритм имеет следующую формулу. Значения a, c и m установлены как 1 103 515 245, 12 345 и 231 соответственно (https://microsin.net/programming/dsp/rand-c-sour- ce-code.html):

                            (5)

Поскольку функция rand возвращает целое число в диапазоне от 0 до 32 767, для получения чисел от 0 до 224 самым простым способом будем использовать три вызова метода Rand()  с последующей конкатенацией (https://learn. microsoft.com/en-us/cpp/c-runtime-library/refe- rence/rand?view=msvc-170). Первой операцией выполнится побитовый сдвиг влево на 8 бит результата предыдущей генерации. Затем выполнится логическое «И» между результатом новой генерации и числом 255. Далее между двумя полученными операндами выполнится логическое «ИЛИ». В коде этот алгоритм выглядит следующим образом:

int randomCRand = (int)rand.Rand() & 255;

randomCRand = randomCRand << 8 | (int)rand.Rand() & 255;

randomCRand = randomCRand << 8 | (int)rand.Rand() & 255;

writer.WriteLine(randomCRand); // Запись результата в файл

Алгоритм Лемера. В дополнение к стандартным алгоритмам Microsoft и Unity для проверки работоспособности приложения был взят довольно простой алгоритм американского математика Д. Лемера, представленный в 1954 году. Формула Лемера выглядит следующим образом:

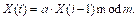                           (6)

Значение константы m = 2 147 483 647 – это максимальное положительное число типа int. Константа a изначально равнялась 16 807, но в 1993 году был предложен более качественный вариант алгоритма, где a = 48 271. Для инициализации генератора Лемера можно использовать любое целочисленное зерно в диапазоне от 1  до 231 (https://learn.microsoft.com/en-us/archive/ msdn-magazine/2016/august/test-run-lightweight-random-number-generation). На практике зерно обычно высчитывается путем преобразования текущих даты и времени в единственное целоечисло. Помимо a и m, в генераторе Лемера используются еще две константы: q = 127 773  и r = 2 836. Приведем фрагмент кода алгоритма Лемера на языке C#:

public double Next()

{   int hi = seed / q;

    int lo = seed % q;

    seed = (a * lo) - (r * hi);

    if (seed <= 0)

seed = seed + m;

    return (seed * 1.0) / m;  }

Переменные hi и lo здесь обозначают верхнюю и нижнюю границы диапазона чисел.

Получение инициирующего числа. У структуры DateTime платформы Microsoft .NET есть свойство Ticks, которое возвращает число тактов, представляющее дату и время экземпляра (https://learn.microsoft.com/en-us/dotnet/api/sys- tem.datetime.ticks?view=net-8.0). Для получения псевдослучайного зерна для алгоритмов  C Rand и Lehmer можно использовать свойство Ticks для получения количества тактов, прошедших, например, со Дня Победы (09.05.1945). Один такт равен 100 наносекундам, поэтому полученное значение будет 19-значным числом, что потребует использования типа long. Теперь для получения псевдослучайного зерна достаточно посчитать остаток от деления количества тактов на 131 072 и преобразовать результат в тип uint. Приведем фрагмент кода класса GetSeedFromTicks, реализующий этот функционал:

DateTime myBirthday = new DateTime(1945, 05, 09);

DateTime currentDate = DateTime.Now; // 1 тик = 100 нс

long elapsedTicks = currentDate.Ticks - myBirthday.Ticks;

long seed; // Зерно = остаток от деления тиков на 65536

seed = (uint)elapsedTicks % 131072;

Debug.Log("Полученное зерно: " + seed);

return seed;

Полученные результаты  и экспериментальная проверка

С использованием игрового движка Unity был разработан 2D-интерфейс приложения для визуализации ГПСЧ (рис. 1).

Центральную часть экрана занимает квад, на который будет накладываться текстура с попиксельным закрашиванием. В правой части располагаются четыре кнопки выбора алгоритмов. При нажатии на любую из них будут сге- нерированы 65 536 псевдослучайных чисел  с помощью выбранного алгоритма и записаны в текстовый файл. В окне ниже отобразится имя файла, соответствующее названию выбранного алгоритма.

Кнопки внизу экрана позволяют выбрать текстовый файл для визуализации, запустить скрипт, который преобразует числа из файла  в цвета текстуры, и сохранить закрашенную текстуру в файл с расширением .PNG в папку Output в директории программы.

На изображениях рисунка 2 визуально не удается выделить какие-либо повторяющиеся структуры или преобладающие цвета. Это значит, что рассмотренные ГПСЧ в первом приближении дают достаточно качественный результат перемешивания и имеет смысл подвергнуть их дальнейшей углубленной оценке при помощи математических методов NIST или Dieharder.

Если же, например, изменить константу a  в алгоритме C Rand на 111, то на изображении проступят четко различимые горизонтальные линии, свидетельствующие о наличии повторений (рис. 3a). На рисунке 3b приведена визуализация повторяющихся числовых последовательностей от 1 до 1 023 – в результате получается красно-черный градиент.

Также визуальной оценке был подвергнут ГПСЧ, описанный в [8], где для выбора зерна используются данные с аппаратных датчиков давления и цвета. Его визуализация представлена на рисунке 3c. Зерно меняется через каждые 1 024 числа. Как можно заметить, внешние датчики также обеспечивают высокое качество перемешивания.

Для визуального сравнения последовательностей псевдослучайных чисел с истинно случайной последовательностью был взят набор из нулей и единиц, сгенерированный на квантовом генераторе компании «КуРэйт». Данный генератор основан на интерференции лазерных импульсов со случайной фазой и использует  в качестве источника энтропии флуктуации  фазы электромагнитного поля в резонаторе полупроводникового лазера [9]. Полученный от него набор данных заранее прошел проверку всеми 15 тестами NIST. Этот случайный набор был разбит на строки по 24 символа (24 бита)  с последующим преобразованием строк в 24-битные числа типа int. На рисунке 3d представлена визуализация итоговой случайной последовательности целых десятичных чисел.

Дальнейшие перспективы  и выводы

Случайные числа играют ключевую роль  в функционировании всей экосистемы блокчейна. Они используются, в частности, для генерации криптографических ключей, обеспе- чивающих безопасность транзакций и защиту пользовательских криптоактивов, выбора узлов-валидаторов, распределения вознаграждений, генерации случайных идентификаторов транзакций или блоков, определения свойств NFT. При этом подходы к получению случайных чисел в блокчейнах и децентрализованных приложениях делятся на две категории: одни решения работают вне цепочки блоков, другие же для генерации чисел и их проверки используют хэши блоков и смарт-контракты.

Самый простой способ получения случайных чисел вне цепочки – обратиться к третьей стороне, поставщику услуг, который по запросу пользователя будет генерировать число и отправлять его в блокчейн. Минус такого подхода очевиден: все участники сети должны доверять честности поставщика (https://pyth. network/blog/secure-random-numbers-for-block- chains).

Для генерации случайных чисел внутри сети можно использовать в качестве источника энтропии хэш будущего блока. Такой подход называется Blockhash. Транзакция запроса сохраняет номер текущего или будущего блока, после чего узлы-валидаторы сети вычисляют его хэш. Как только хэш станет доступным, транзакция раскрытия вернет его значение. Однако здесь участникам сети тоже приходится доверять честности стороннего участника – валидатора, который может переопределить порядок транзакций или пренебречь определен- ной транзакцией ради изменения хэша блока, что приведет к гарантированному выпадению желаемого случайного числа.

Верифицируемая случайная функция (VRF) призвана защитить результат от влияния со сто- роны участников сети. Это криптографический примитив, псевдослучайная функция, которая представляет общедоступное достоверное доказательство своего вывода на основе открытых входных данных и закрытого ключа. Ее можно записать так [10]:

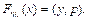                                        (7)

В уравнении (7) выходное значение y выглядит случайным, но однозначно вычисляется на основе входных данных x и секретного клю- ча SK. Функция возвращает доказательство p, которое каждый участник сети может проверить, чтобы убедиться, что y является корректным результатом вычислений. В блокчейне x представляет собой комбинацию из пользовательских данных и хэшей блоков. Поставщик услуг с секретным ключом SK находится вне сети. Он отслеживает появление в блокчейне запросов на генерацию случайного числа и отправляет ответы в цепочке (y, p). Транзакция раскрытия проверяет доказательство p, чтобы убедиться, что y является правильным значением. Однако главный недостаток использова- ния VRF опять же лежит в области доверия поставщику, поскольку именно он решает, стоит ли отправлять сгенерированное случайное число в блокчейн или нет. К тому же вычисление функции и доказательства могут потребовать несколько транзакций, за проведение которых участнику придется платить комиссию сети.

Как можно заметить, блокчейны предъявляют особые требования к случайности результатов генерации, поскольку получение неслучайного числа может свидетельствовать о компрометации механизма генерации злоумышленником или попытке поставщика услуг подтасовать результаты. Предлагаемое решение является первым этапом на пути оценки качества и достоверности генерации случайных чисел. Визуализация позволяет проводить быструю оценку последовательностей целых чисел и выявлять  в них артефакты, паттерны, повторения и области неравномерного распределения для дальнейшего углубленного анализа популярными математическими методами.

Список литературы

1.   Ключарев П.Г. О статистическом тестировании блочных шифров // Математика и математическое моделирование. 2018. № 5. С. 35–56. doi: 10.24108/mathm.0518.0000132.

2.   Ryabko B. Time-adaptive statistical test for random number generators. Entropy, 2020, vol. 22, no. 6,  art. 630. doi: 10.3390/e22060630.

3.   Marsaglia G. The marsaglia random number CDROM including the diehard battery of tests of randomness. 1997. URL: http://www.stat.fsu.edu/pub/diehard/ (дата обращения: 21.05.2024).

4.   Sleem L., Couturier R. TestU01 and Practrand: Tools for a randomness evaluation for famous multimedia ciphers. Multimedia Tools and Applications, 2020, vol. 79, pp. 24075–24088. doi: 10.1007/s11042-020-09108-w.

5.   Bassham L., Rukhin A., Soto J. et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications. NIST SP, 2010, 800-22 Rev. 1. doi: 10.6028/NIST.SP.800-22R1A.

6.   Dziala T.R. Collatz-Weyl generators: high quality and high throughput parameterized pseudorandom number generators // Декабрь 2023. ArXiv, doi: 10.48550/arXiv.2312.17043.

7.   Crocetti L., Di Matteo S., Nannipieri P., Fanucci L., Saponara S. Design and test of an integrated random number generator with all-digital entropy source. Entropy, 2022, vol. 24, no. 2, art. 139. doi: 10.3390/e24020139.

8.   Булгаков Д.А. Генерация случайных чисел для интерактивных приложений с использованием внешних датчиков // Изв. вузов. Приборостроение. 2024. Т. 67. № 4. С. 338–344. doi: 10.17586/0021-3454-2024-67-4-338-344.

9.   Шаховой Р. QRate Chaos – квантовый генератор случайных чисел // QRate. Pat. № 2721585.  URL: https://www.goqrate.com/projects/qrate-chaos-kvantovyy-generator-sluchaynykh-chisel-pat-2721585/ (дата обращения: 21.05.2024).

10. Werapun W., Karode T., Jakapan S., Arpornthip T., Sangiamkul E. NativeVRF: A simplified decentralized random number generator on EVM blockchains. Systems, 2024, vol. 11, no. 7, art. 326. doi: 10.3390/systems11070326.

References

1. Klyucharev, P.G. (2018) ‘On statistical testing of block ciphers’, Math. and Math. Modeling, (5), pp. 35–56 (in Russ.). doi: 10.24108/mathm.0518.0000132.

2. Ryabko, B. (2020) ‘Time-adaptive statistical test for random number generators’, Entropy, 22(6), art. 630. doi: 10.3390/e22060630.

3. Marsaglia, G. (1997) The Marsaglia Random Number CDROM Including the Diehard Battery of Tests of Randomness, available at: http://www.stat.fsu.edu/pub/diehard/ (accessed May 21, 2024).

4. Sleem, L., Couturier, R. (2020) ‘TestU01 and Practrand: Tools for a randomness evaluation for famous multimedia ciphers’, Multimedia Tools and Applications, 79, pp. 24075–24088. doi: 10.1007/s11042-020-09108-w.

5. Bassham, L., Rukhin, A., Soto, J. et al. (2010) ‘A statistical test suite for random and pseudorandom number generators for cryptographic applications’, NIST SP, (800-22 Rev. 1). doi: 10.6028/NIST.SP.800-22R1A.

6. Dziala, T.R. Collatz-Weyl generators: high quality and high throughput parameterized pseudorandom number generators // December 2023, ArXiv. doi: 10.48550/arXiv.2312.17043.

7. Crocetti, L., Di Matteo, S., Nannipieri, P., Fanucci, L., Saponara, S. (2022) ‘Design and test of an integrated random number generator with all-digital entropy source’, Entropy, 24(2), art. 139. doi: 10.3390/e24020139.

8. Bulgakov, D.A. (2024) ‘Random number generation for interactive applications using external sensors’, J. of Instrument Eng., 67(4), pp. 338–344 (in Russ.). doi: 10.17586/0021-3454-2024-67-4-338-344.

9. Shakhovoy, R. ‘QRate Chaos – quantum random number generator’, QRate, Pat. № 2721585, available at: https://www.goqrate.com/projects/qrate-chaos-kvantovyy-generator-sluchaynykh-chisel-pat-2721585/ (accessed May 21, 2024) (in Russ.).

10. Werapun, W., Karode, T., Jakapan, S., Arpornthip, T., Sangiamkul, E. (2024) ‘NativeVRF: A simplified decentra- lized random number generator on EVM blockchains’, Systems, 11(7), art. 326. doi: 10.3390/systems11070326.