Введение. Моделирование структуры импортозамещения в российской экономике представляет собой задачу, решаемую с помощью не только экономическо-математических, но информационно-технологических методов, в контексте поиска оптимальных решений по перераспределению инвестиций, рабочей силы, промежуточного продукта между отраслями.
Разработанные ранее подходы к моделированию импортозамещения основаны на целевой функции выпуска продукции для внутреннего рынка (по критерию оптимизации для достижения его максимума), в качестве аргументов которой предлагаются:
– конкурентоспособность отечественной продукции и производительность отраслевых предприятий по ее выпуску [1];
– зависимость экономики от импорта определенной продукции, объемы ее производства и затраты на выпуск внутри страны [2];
– промежуточное и конечное потребление импорта в экономике, выпуск отечественными предприятиями [3];
– выпуск в доминирующей модели российских рынков – монополий, их фондовооруженность, производительность и капиталоотдача [4];
– дополнительные налоги, получаемые го-сударством от предприятий, участвующих в импортозамещении, увеличение заработной платы и социальных выплат в целом по экономике, количество новых рабочих мест [5].
В зарубежной литературе моделирование импортозамещения рассматривается с позиции оптимизации общего равновесия при измене- нии соотношения экспорта и импорта [6], изме- нения импорта и внутреннего отраслевого выпуска в ответ на изменения внутренних цен [7], выпуска в ресурсовозобновляемом и невозобновляемом секторах экономики [8], выгод и издержек от протекционизма [9].
В целом в литературе преобладают подходы к моделированию импортозамещения, в основе которых лежат переменные, характеризующие экономическую динамику (затраты, выпуск, налоги, импорт, экспорт и пр.). Такие модели достаточно изучены, и нахождение значений их целевых функций представляется сравнительно простым. В свою очередь, в условиях интенсивного воздействия внешних шоков (таких как санкции и эмбарго) на российскую экономику традиционные динамические модели теряют эффективность, поскольку доступ к ря- ду ресурсов значительно сокращается, а затраты на выпуск продукции для внутреннего рынка растут, что снижает конкурентоспособность – важный аргумент во многих подходах.
Поэтому, учитывая потери российской экономики от санкций, в данной работе предлагается более соответствующий проблеме подход к моделированию импортозамещения, основанный на оптимизации ее структуры. Следует отметить, что исследований, посвященных разработке программных продуктов в данной области, мало, исключением можно считать разработку алгоритмов [10, 11] и предложение модулей оптимального межотраслевого распределения ресурсов [12].
В связи с этим целесообразно создание программного продукта для модели структуры импортозамещения, целевая функция которой имеет два основных аргумента – объемы и эффективность использования труда и капитала как главных факторов производства (новые технологии учитываются как константа [13], а изменения в уровне образования работников – как экзогенный параметр [14]).
Модели и методы
Целевая функция в модели структуры импортозамещения. С учетом сказанного на уровне производства одного продукта на одном предприятии целевая функция модели структуры импортозамещения будет выглядеть следующим образом:
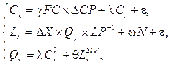 (1)
(1)
где Cx – функция инвестиций для импортозамещения с учетом прироста новых технологий и воздействия внешних шоков на отечественный рынок капитала; FC – стоимость основного капитала на предприятии, занятого выпуском одного продукта; Lx – функция трудовых ресурсов для импортозамещения с учетом изменения доли отечественной продукции DX, заданной в отраслевых программах; Qx – функция выпуска продукции с учетом двух факторов – труда и капитала (производственная функция); λ – показатель прироста производимого продукта от внедрения передовых производственных технологий (технологический мультипликатор); γ – показатель, учитывающий воздействие внешних шоков (в т.ч. санкций) на основные средства (потребность в дополнительных инвестициях): потери от ухода иностранных компаний, от ограничения доступа на мировой рынок капитала, от технологических ограничений; ε – ошибки регрессионных вычислений: ε ~ N(0, Σ), где Σ – ковариационная матрица ошибок ϵt [15], в данной модели равная 0; LP – производительность труда; ∆LP – изменение производительности труда за счет внедрения новых передовых производственных технологий в процессе импортозамещения; ω – показатель потерь рын- ка труда вследствие внешних шоков (дополнительная потребность в рабочей силе); N – число работников, занятых в производстве продукта в целях импортозамещения; Θ – экзогенный параметр, учитывающий потребность в развитии профессионального образования в условиях внешних шоков и технологических ограничений.
Применительно к модели отраслевой структуры импортозамещения в национальной экономике целевая функция модели структуры импортозамещения для выпуска в отрасли i про- дукта j может быть представлена в следующем виде:
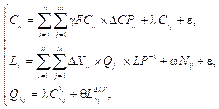 (2)
(2)
где n – конечное число отраслей i в экономике, занятых в импортозамещении; FCij – стоимость основного капитала отрасли i, занятой в выпуске продукта j; ∆CPij – изменение фондоотдачи в отрасли i по выпуску продукта j;  – объем инвестиций в отрасли i, необходимый для импортозамещения продукта j; ∆Xij – изменение доли продукта j отрасли i на внутреннем рынке;
– объем инвестиций в отрасли i, необходимый для импортозамещения продукта j; ∆Xij – изменение доли продукта j отрасли i на внутреннем рынке; 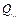 – текущий (фактический) объем выпуска продукта j в отрасли i; Nij – число работников отрасли i, занятых в импортозамещении продукта j; Cxj – функция инвестиций для импортозамещения продукта j в отрасли i;
– текущий (фактический) объем выпуска продукта j в отрасли i; Nij – число работников отрасли i, занятых в импортозамещении продукта j; Cxj – функция инвестиций для импортозамещения продукта j в отрасли i; 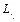 – функция трудовых ресурсов для импортозамещения продукта j в отрасли i;
– функция трудовых ресурсов для импортозамещения продукта j в отрасли i;  – производственная функция для импортозамещения продукта j в отрасли i.
– производственная функция для импортозамещения продукта j в отрасли i.
Далее описаны значения нормированного весового показателя факторов, определяющих их значимость, которые были определены в ходе построения матрицы критериев n (конечное значение количества видов структуры импортозамещения) и m (количество видов шоков).
γ – эндогенный показатель, учитывающий воздействие внешних шоков (в том числе санкций) на основные средства – потребность в дополнительных инвестициях: потери от ухода иностранных компаний – эндогенный фактор шокового воздействия на воспроизводственную структуру, aij = 0,170; потери от ограничения доступа на мировой рынок капитала – эндогенный фактор воздействия шоков на структуру факторов производства, aij = 0,044; потери от технологических ограничений – эндогенный фактор шокового воздействия на технологическую структуру, aij = 0,325.
Авторы использовали среднее квадратичное отклонение для усреднения весовых показателей воздействия шоков и санкций на инвестирование основных средств предприятий, занятых в импортозамещении, при котором γ = 1 + + aijср.кв = 1 + 0,149 = 1,149.
λ – экзогенный показатель прироста производимого продукта от внедрения передовых производственных технологий (технологический мультипликатор) – экзогенный фактор шокового воздействия на технологическую структуру, aij = 0,139. Тогда λ = 1 + aij = 1,139.
ω – экзогенный показатель потерь рынка труда вследствие внешних шоков (дополнительная потребность в рабочей силе вследствие внешних санкций и утечки мозгов и рук), aij = 0,68. Тогда ω = 1 + aij = 1,68.
Θ – экзогенный параметр, учитывающий потребность в развитии профессионального образования в условиях внешних шоков и технологических ограничений, aij = 0,136. Тогда Θ = 1 + aij = 1,136.
Описание документации вычислительного обеспечения представленной выше модели предназначено для пользователей, которые хо- тят понять структуру, функции и взаимодействие классов и модулей программного средства, разработанного для решения задачи межотраслевого распределения факторов производства (труда и капитала) в условиях внешних шоков с целью импортозамещения.
Разработка программного и алгоритмического обеспечения
Классы и структура их связей. Програм-мное средство состоит из нескольких основных классов, каждый из которых играет определенную роль в расчетах и моделировании.
Класс Constants отвечает за хранение и управ- ление константами, используемыми в расчетах. Константы включают в себя такие параметры, как погрешность регрессионных вычислений (_epsilon), показатель влияния внешних шоков на основные средства (_gamma), показатель прироста производимого продукта от внедрения новых технологий (_lambda), показатель потерь рынка труда вследствие внешних шоков (_omega) и потребность в развитии профессионального образования (_teta). Эти параметры могут быть заданы или изменены пользователем через методы класса.
class Constants: """ Класс с константами """ def __init__(self): self._epsilon = 0 self._gamma = 1.149 self._lambda = 1.139 self._omega = 1.068 self._teta = 1.136 def set_epsilon(self, new_value: float) -> None: """ Задать эпсилон :param new_value: новое значение """ self._epsilon = new_value def set_gamma(self, new_value: float): """ Задать гамма :param new_value: новое значение """ self._gamma = new_value def set_lambda(self, new_value: float): """ Задать лямбда :param new_value: новое значение """ self._lambda = new_value
def set_omega(self, new_value: float): """ Задать омега :param new_value: новое значение """ self._omega = new_value
def set_teta(self, new_value: float): """ Задать тета :param new_value: новое значение """ self._teta = new_value
Класс Variables предназначен для хранения переменных, необходимых для расчетов. В него входят такие переменные, как количество отраслей (n), количество продуктов (m), массивы стоимости основного капитала (FC_ array), изменения фондоотдачи (delta_CP_array), изменения фондоотдачи на уровне отрасли (C_r_array), изменения доли отечественного продукта (delta_X_array), фактический объем выпуска продукции (Q_f_array), количество работников (N_array), производительность труда (lp) и изменение производительности труда (delta_lp). Класс также содержит массивы для хранения результатов расчетов C_x, L_x и Q_x.
class Variables: """ Класс переменных для расчета """ def __init__(self, **kwargs): self.n = kwargs.get('n') self.m = kwargs.get('m') self.FC_array = = kwargs.get('FC_array') self.delta_CP_array = = kwargs.get('delta_CP_array') self.C_r_array = = kwargs.get('C_r_array') self.delta_X_array =
= kwargs.get('delta_X_array') self.Q_f_array =
= kwargs.get('Q_f_array') self.N_array = kwargs.get('N_array') self.lp = kwargs.get('lp') self.delta_lp = kwargs.get('delta_lp') # Инициализация массивов в этом классе self.C_x_array = [[0 for _ in range(self.m)] for _ in range(self.n)] self.L_x_array = [[0 for _ in range(self.m)] for _ in range(self.n)] self.Q_x_array = [[0 for _ in range(self.m)] for _ in range(self.n)]
Для вычисления массива C_x используется класс C_x_calculator. Этот класс включает метод _calculate_C_x_array, который выполняет необходимые расчеты на основе значений констант и переменных. Метод get_result возвращает результат вычислений.
class C_x_calculator: """ Класс подсчета массива C_x """ def __init__(self, constants_obj: Constants, variables_obj: Variables): self.C_x_result = self._calculate_C_x_array(constants_obj, variables_obj) def _calculate_C_x_array(self, constants_obj, variables_obj): """ Посчитать массив C_x """ for i in range(variables_obj.n): for j in range(variables_obj.m): # Вычисляем значение для текущего элемента массива value = constants_obj._gamma * variables_obj.FC_array[i][j] * variables_obj.delta_CP_array[i][ j] + constants_obj._lambda * \ variables_obj.C_r_array[i][j] + constants_obj._epsilon # Запишем вычисленное значение в элемент массива variables_obj.C_x_array[i][j] = value return variables_obj.C_x_array def get_result(self) -> List[List[float]]: """ Вернуть результат :return: массив """ return self.C_x_result
Аналогично класс L_x_calculator выполняет вычисления для массива L_x с помощью метода _calculate_L_x_array и предоставляет результаты через метод get_result.
class L_x_calculator: """ Класс подсчета массива L_x """ def __init__(self, constants_obj: Constants, variables_obj: Variables): self.L_x_result = self._calcu- late_L_x_array(constants_obj, variables_obj) def _calculate_L_x_array(self, constants_obj: Constants, variables_obj: Variables): """ Посчитать массив L_x """ for i in range(variables_obj.n): for j in range(variables_obj.m): # Вычисляем значение для текущего элемента массива value = variables_obj.delta_X_array[i][j] * variables_obj.Q_f_array[i][j] * variables_obj.lp ** ( -1) + constants_obj._omega * \ variables_obj.N_array[i][j] + constants_obj._epsilon # Запишем вычисленное значение в элемент массива variables_obj.L_x_array[i][j] = value return variables_obj.L_x_array def get_result(self) -> List[List[float]]: """ Вернуть результат :return: массив """ return self.L_x_result
Класс Q_x_calculator отвечает за вычисление массива Q_x, используя метод _calculate_ Q_x_array и предоставляя результаты через метод get_result.
class Q_x_calculator: """ Класс подсчёта массива Q_x """ def __init__(self, constants_obj: Constants, variables_obj: Variables): self.Q_x_result = self._calculate_Q_x_array(constants_obj, variables_obj) def _calculate_Q_x_array(self, constants_obj: Constants, variables_obj: Variables): """ Посчитать массив Q_x """ for i in range(variables_obj.n): for j in range(variables_obj.m): # Вычисляем значение для текущего элемента массива value = con- stants_obj._lambda * variables_obj.C_x_array[i][ j] ** constants_obj._lambda + constants_obj._teta * variables_obj.L_x_array[i][ j] ** variables_obj.delta_lp # Запишем вычисленное значение в элемент массива variables_obj.Q_x_array[i][j] = value return variables_obj.L_x_array def get_result(self) -> List[List[float]]: """ Вернуть результат :return: массив """ return self.Q_x_result
Для координации выполнения всех расчетов служит класс FormulaSolve. Он управляет процессом решения целевой функции модели структуры импортозамещения. В его методы входят _solve, который выполняет необходимые вычисления, и методы get_C_x, get_L_x, get_Q_x для получения результатов соответствующих массивов.
class FormulaSolve: """ Класс решения целевой функции модели структуры импортозамещения """ def __init__(self, constants_obj: Constants, variables_obj: Variables): self.C_x_obj = None self.L_x_obj = None self.Q_x_obj = None self._solve(constants_obj, variables_obj) def _solve(self, constants_obj: Constants, variables_obj: Variables): """ Посчитать целевую функцию """ self.C_x_obj = C_x_calculator(constants_obj, variables_obj) self.L_x_obj = L_x_calculator(constants_obj, variables_obj) self.Q_x_obj = Q_x_calculator(constants_obj, variables_obj) def get_C_x(self) -> List[List[float]]: """ Получить массив C_x :return: двумерный массив """ return self.C_x_obj.get_result() def get_L_x(self) -> List[List[float]]: """ Получить массив L_x :return: двумерный массив """ return self.L_x_obj.get_result() def get_Q_x(self) -> List[List[float]]: """ Получить массив Q_x :return: двумерный массив """ return self.Q_x_obj.get_result()
Взаимодействие классов. Пользователь задает через интерфейс значения констант и переменных, которые затем передаются в соответствующие классы Constants и Variables. После этого классы C_x_calculator, L_x_calculator и Q_x_calculator выполняют необходимые рас- четы. Результаты расчетов координируются и сохраняются классом FormulaSolve. Взаимодействие классов отражено на рисунке 1.

 Формат команд и процедур. Команды и процедуры в приложении выполняются через методы классов. Пользователь взаимодействует с приложением через графический интерфейс, который вызывает соответствующие методы для выполнения расчетов и отображения результатов. Работа алгоритма в виде блок-схемы представлена на рисунке 2.
Формат команд и процедур. Команды и процедуры в приложении выполняются через методы классов. Пользователь взаимодействует с приложением через графический интерфейс, который вызывает соответствующие методы для выполнения расчетов и отображения результатов. Работа алгоритма в виде блок-схемы представлена на рисунке 2.
Работа СУБД. Используемая в приложении БД состоит из двух основных таблиц – variables и results. Таблица variables хранит переменные, используемые в расчетах, такие как количество отраслей (n), количество продуктов (m), массивы стоимости основного капитала (FC_array), изменения фондоотдачи (delta_CP_array), изменения фондоотдачи на уровне отрасли (C_r_array), изменения доли отечественного продукта (delta_X_array), фактический объем выпуска продукции (Q_f_array), количество работников (N_array), производительность тру- да (lp) и изменение производительности труда (delta_lp). Каждая запись в таблице variables идентифицируется уникальным идентификато- ром (uid) (http://www.swsys.ru/uploaded/image/ 2024-3/15.jpg).
Таблица results хранит результаты расчетов, такие как массивы C_x, L_x и Q_x. Эти результаты связываются с соответствующими переменными через uid (http://www.swsys.ru/uploa- ded/image/2024-3/16.jpg).
Связь между таблицами обеспечивается использованием uid, что позволяет отслеживать все вычисления, связанные с конкретным набором переменных.
Результаты разработки
Основная функция приложения. Основная функция приложения заключается в мо- делировании структуры импортозамещения в условиях внешних шоков. Это позволяет пользователям оценивать воздействие различных факторов на производственные процессы и планировать необходимые изменения для повышения эффективности импортозамещения.
Алгоритм работы приложения. Работа приложения начинается с ввода данных пользователем через графический интерфейс. Пользователь вводит значения переменных и констант, таких как количество отраслей, количество продуктов, значения массивов стоимости основного капитала, изменения фондоотдачи, фактический объем выпуска продукции и количество работников. Введенные данные сохраняются в таблице variables БД.
После ввода всех необходимых данных пользователь нажимает кнопку для запуска расчетов. Программа выполняет расчеты, используя методы классов C_x_calculator, L_x_calculator и Q_x_calculator. Результаты расчетов сохраняются в таблице results БД и связываются с соответствующими переменными через uid.
Результаты расчетов отображаются на экра- не в виде таблиц и графиков. Пользователь может просмотреть массивы C_x, L_x и Q_x, а также другие производные данные. Интерфейс предоставляет возможность визуализации данных для удобства анализа.
Графический интерфейс. Графический интерфейс приложения состоит из нескольких основных компонентов, обеспечивающих удоб- ный ввод данных, запуск расчетов и просмотр результатов (http://www.swsys.ru/uploaded/ima- ge/2024-3/17.jpg).
Пользователь вводит значения переменных и констант через соответствующие поля ввода. Например, он может ввести количество отраслей (n) и количество продуктов (m), а также значения массивов стоимости основного капитала, изменения фондоотдачи, изменения доли отечественного продукта, фактического объема выпуска продукции и количества работ- ников. Для каждого массива предусмотрены кнопки, открывающие диалоговые окна для ввода значений (http://www.swsys.ru/uploaded/ image/2024-3/21.jpg).
После ввода всех данных пользователь подтверждает ввод и нажимает кнопку для запуска расчетов. Результаты расчетов отображаются на экране в виде таблиц и графиков, что позво- ляет пользователю анализировать данные и принимать решения на основе полученной информации.
Таблицы отображают результаты расчетов массивов C_x, L_x и Q_x, а графики визуально представляют эти данные для удобства анализа.
Заключение
Математическое моделирование структуры импортозамещения на основе определения оптимальных пропорций двух факторов производства – труда и капитала, а также их эффективности (производительности и фондоотдачи) дает возможность преодолеть те ограничения моделей импортозамещения, учитывающих динамические характеристики производства (выпуск, затраты, субсидии и пр.), которые усиливаются в периоды действия внешних шоков, таких как санкционные ограничения. Для этого в статье предложен подход к созданию программного средства, предназначенного для моделирования инвестиций и занятости, выпуска в импортозамещающих отраслях, включающего ряд основных классов (в том числе класс решения целевой функции модели структуры импортозамещения), диаграмму, отражающую порядок их взаимодействия, алгоритм вызова соответствующих методов для выполнения расчетов и отображения результатов, а также систему управления БД.
Разработанный алгоритм работы приложения предусматривает ввод данных – переменных и констант – через графический интерфейс, запуск расчетов, сохранение результатов и вывод их на экран в виде графиков и таблиц. С учетом этого предложенное программное средство может быть использовано в процессе создания отраслевых программ импортозамещения и их корректировки в условиях усиления внешних шоков, а также для гармонизации федеральных и региональных направлений промышленной политики.
Дальнейшее направление исследования связано с развитием СУБД, отражающих результаты воздействия внешних шоков на структуру и масштаб импортозамещения.
Список литературы
1. Уразаева Л.Ю., Галимов И.А. Математическое моделирование импортозамещения // Вестн. евразийской науки. 2022. Т. 14. № 3. С. 1–9.
2. Стрижкова Л.А. Использование таблиц «затраты–выпуск» при оценке зависимости российской экономики от импорта и процессов импортозамещения // Вопросы статистики. 2016. № 5. С. 3–22.
3. Моисеев Н.А., Внуков И.А., Сокерин П.О. Оценка эффектов различных вариантов импортозамещения методом «затраты–выпуск» на примере Российской Федерации // Экономика и математические методы. 2023. Т. 59. № 1. С. 30–47. doi: 10.31857/S042473880024869-4.
4. Кутернин М.И. Моделирование комплексного процесса импортозамещения и модернизации экономики страны при управлении через ее естественные монополии // Вестн. университета. 2017. № 9. С. 39–44.
5. Палаш С.В. Моделирование экономических эффектов импортозамещения в обрабатывающей промышленности Российской Федерации // Науч.-технич. ведомости СПбГПУ. Экономические науки. 2019. Т. 12. № 1. С. 59–69.
6. Clements K.W., Mariano M.J.M., Verikios G. Foreign-domestic substitution, import penetration and CGE modelling. Applied Economics, 2021, vol. 53, no. 35, pp. 4080–4099. doi: 10.1080/00036846.2021.1897072.
7. Енина Е.С. Модель вовлечения в процесс импортозамещения: маркетинговый подход // Экономика и управление. 2022. Т. 28. № 9. С. 905–911. doi: 10.35854/1998-1627-2022-9-905-911.
8. Nurkomariyah S., Vierke I.M. Import substitution in circular economy perspective: A study on textile and apparel industry. IJSSHR, 2023, vol. 6, no. 12, pp. 12–33. doi: 10.47191/ijsshr/v6-i12-33.
9. Cherif R., Hasanov F. The pitfalls of protectionism: Import substitution vs. export-oriented industrial policy. JICT, 2024, vol. 24, art. 14. doi: 10.1007/s10842-024-00414-9.
10. Кордюков Р.Ю., Допира Р.В., Иванова А.В., Абу-Абед Ф.Н., Мартынов Д.В. Модель и алгоритмизация оптимизационной задачи о назначениях в условиях дополнительных ограничений // Программные продукты и системы. 2016. Т. 29. № 2. С. 16–22. doi: 10.15827/0236-235X.114.016-022.
11. Моисеев Н.А., Ахмадеев Б.А. Алгоритм оценки импортозамещения на основе таблиц затрат–выпуска // Вестн. РЭА им. Г.В. Плеханова. 2021. № 3. С. 117–129. doi: 10.21686/2413-2829-2021-3-117-129.
12. Абу-Абед Ф.Н., Жиронкин С.А. Моделирование структуры импортозамещения на базе модели системы оптимального распределения // Программные продукты и системы. 2023. Т. 36. № 4. С. 644–653. doi: 10.15827/0236-235X.144.644-653.
13. Саидзода И.М., Ризоев С.С. Компьютерное исследование производственной функции Кобба–Дугласа с использованием электронной таблицы MS Excel // Вестн. ТГПУ. 2022. № 2. C. 80–85.
14. Сазонов А.А., Сазонова М.В. Выявление свойств экзогенности в моделях прогнозирования экономического роста // Фундаментальные и прикладные исследования: проблемы и результаты. 2016. № 24. С. 176–180.
15. Коротких О. Межстрановая BVAR-модель внешнего сектора // Деньги и кредит. 2020. Т. 79. № 4. С. 98–112. doi: 10.31477/rjmf.202004.98.
References
1. Urazaeva, L.Yu., Galimov, I.A. (2022) ‘Mathematical modeling of import substitution’, The Eurasian Scientific J., 14(3), pp. 1–9 (in Russ.).
2. Strizhkova, L.A. (2016) ‘Using “input–output” tables in estimating the dependence of Russian economy on import and import substitution processes’, Bull. of Statistics, (5), pp. 3–22 (in Russ.).
3. Moiseev, N.A., Vnukov, I.A., Sokerin, P.O. (2023) ‘Evaluation of the effects from various ways of import substitu-tion “input–output” method: Evidence from the Russian Federation’, Economics and Mathematical Methods, 59(1), pp. 30–47 (in Russ.). doi: 10.31857/S042473880024869-4.
4. Kuternin, M.I. (2017) ‘Modeling of the import substitution and national economy modernization complex process with a management through the natural monopolies of the country’, Vestn. Univ., (9), pp. 39–44 (in Russ.).
5. Palash, S.V. (2019) ‘Modeling the economic effects of import substitution in Russian manufacturing industry’, SPbSTU J. Economics, 12(1), pp. 59–69 (in Russ.).
6. Clements, K.W., Mariano, M.J.M., Verikios, G. (2021) ‘Foreign-domestic substitution, import penetration and CGE modelling’, Applied Economics, 53(35), pp. 4080–4099. doi: 10.1080/00036846.2021.1897072.
7. Enina, E. (2022) ‘Model of involvement in import substitution: A marketing approach’, Economics and Management, 28(9), pp. 905–911 (in Russ.). doi: 10.35854/1998-1627-2022-9-905-911.
8. Nurkomariyah, S., Vierke, I.M. (2023) ‘Import substitution in circular economy perspective: A study on textile and apparel industry’, IJSSHR, 6(12), pp. 12–33. doi: 10.47191/ijsshr/v6-i12-33.
9. Cherif, R., Hasanov, F. (2024) ‘The pitfalls of protectionism: Import substitution vs. export-oriented industrial po-licy’, JICT, 24, art. 14. doi: 10.1007/s10842-024-00414-9.
10. Kordyukov, R.Yu., Dopira, R.V., Ivanova, A.V., Abu-Abed, F.N., Martynov, D.V. (2016) ‘A model and algorith-mization of the assignment problem under additional constraints’, Software & Systems, 29(2), pp. 16–22 (in Russ.). doi: 10.15827/0236-235X.114.016-022.
11. Moiseev, N.A., Akhmadeev, B.A. (2021) ‘Algorithm of estimating import-substitution based on costs – output tables’, Bull. of the Russian Plekhanov University of Economics, 3(117), pp. 117–129 (in Russ.). doi: 10.21686/2413-2829-2021-3-117-129.
12. Abu-Abed, F.N., Zhironkin, S.A. (2023) ‘Russian import-substitution structure based on an optimal distribution system model’, Software & Systems, 36(4), pp. 644–653 (in Russ.). doi: 10.15827/0236-235X.144.644-653.
13. Saidzoda, I.M., Rizoev, S.S. (2022) ‘Computer study of Cobb–Douglas production function using MS excel spread-sheet’, Herald TSPU, (2), pp. 80–85 (in Russ.).
14. Sazonov, A.A., Sazonova, M.V. (2016) ‘Identification of exogeneity properties in eco-nomic growth forecasting models’, Fundamental and Applied Research: Problems and Results, (24), pp. 176–180 (in Russ.).
15. Korotkikh, O. (2020) ‘A multi-country BVAR model for the external sector’, Russ. J. of Money and Finance, 79(4), pp. 98–112 (in Russ.). doi: 10.31477/rjmf.202004.98.



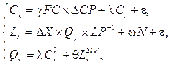 (1)
(1)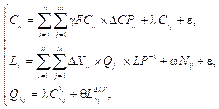 (2)
(2)

