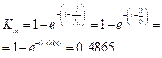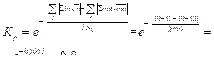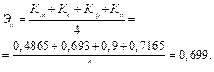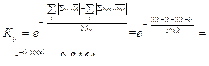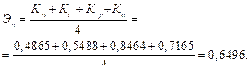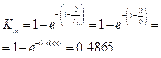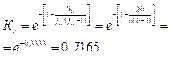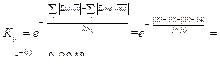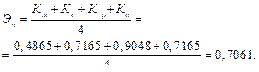Введение. Постоянное усложнение систем, искусственных организационно-технических систем в первую очередь, создаваемых человеком в разных областях деятельности, привело не только к осознанию необходимости предвидеть результаты длительных и дорогостоящих работ по созданию таких систем, но и к поиску инструментария для этого. Поиск шел в нап- равлении наработки способности увидеть и оце- нить функционирование разрабатываемой системы раньше, чем она будет создана физически.

Целью создания любой системы является ее функционирование. Характер функционирования системы в пределах ее морфологических возможностей определяется управлением работой системы. Именно особенности функционирования системы определяют и ее морфологию, и ее материально-информационные потоки.

Известно, что функциональная модель есть графическое представление функционирования систем и объектов [1]. Функциональная модель может использоваться как для анализа процессов протекающих в существующих системах, так и при проектировании новых сис- тем для синтеза их структур [2]. Следует отметить, что анализ функциональных моделей в настоящее время выполняется на качественном уровне путем анализа структуры связей между отдельными функциями моделируемого процесса, сравнения различных структур процесса и процессов между собой. Незначительное количество имеющихся источников и документов по методологии функционального моделирования не приводят методов аналитического количественного анализа функциональных моделей и процессов ими описываемых, а приведенные источники относятся к базовым, что,  в свою очередь, подчеркивает актуальность статьи, ее новизну и практическую значимость.

Функциональную модель, представленную в нотации технологии IDEF0 [2], можно рассматривать как орграф и, следовательно, анализировать с помощью матрицы смежностей функций процесса между собой [3].

Эффективность процесса (Эп) определяется как среднее арифметическое четырех коэффициентов: масштабного коэффициента процес- са (Kм), оценивающего количество функций  в процессе; коэффициента связанности функций процесса (Kс), оценивающего коммуникативность функций в процессе; коэффициента равномерности распределения функций в процес- се (Kр); коэффициента изолированности функций, определяющего общее число несвязанных функций, функций, не имеющих входов или выходов (Kи) [3].

Сложные иерархические системы имеют многоуровневое взаимодействие между ее элементами. Система более высокого уровня выдвигает цель системе более низкого уровня, которая, в свою очередь, выступает как средство для реализации этой цели. Для функционирования системы эти цели и средства их реализации должны быть согласованы между собой [4].

Рассмотрим способы управления сложными системами [5]:

Централизованный способ управления обеспечивает использование всех функций и связей между отдельными функциями моделируемого процесса, при использовании единой функции управления на всех уровнях иерархии.

Децентрализованное управление предусматривает автономные действия отельных функций без единого управления.

Сетецентрическое управление представляет собой матричный информационно-управляющий процесс, в основе которого лежит глобальная информационная взаимосвязь всех функций, интегрированных в единое информационное пространство.

Для сетецентрических систем характерна не только вертикальная интеграция между ее процессами, но и широко развитая сеть горизонтальных связей на одном и том же уровне управления между разнородными процессами системы, которые являются источниками и потребителями циркулирующей в системе инфор- мации.

Такие системы характеризуются принципами открытости, самоорганизации, слабой иерархии в контуре принятия решений и способностью порождать цели внутри себя [1].

При анализе сложных систем управления промоделируем каждый из способов более подробно. Моделирование процессов сложных систем выполним с использованием метода функционального моделирования [6–8].

Процесс действий сложных систем при централизованном способе управления представлен на рисунке 1 в нотации технологии IDEF0. Процесс включает в себя шесть процедурных функций (А1…А6), выполняющих, например, обработку информации, и одну специфическую функцию управления процессом (А0), связанные между собой прямыми и обратными функциональными связями. Процесс имеет два вхо- да из внешней среды (может быть из другого процесса – Out1, Out2) и два выхода во внешнюю среду (во внешние процессы – In1, In2). Как видим, входы из внешней среды осуществляется через функцию А1, А4, обеспечивающую обработку входной информации и ее передачу другим функциям. Выходы во внешнюю среду осуществляется функциями А3, А6, которые, решают основные задачи процесса, остальные функции выполняют обеспечивающие задачи [9]. Следует заметить, что количество входов и выходов в общем случае может быть любым и определяется только структурой исследуемого процесса [3].

Интерпретируя функциональную модель как орграф, сформируем матрицу связей функций моделируемого процесса (табл. 1). В матрице по строкам единицами и нулями записаны входы в функции, по столбцам соответственно получаем выходы из функций. Суммы входов по строкам и выходов по столбцам позволяют ранжировать функции по степени важности  в исследуемом процессе. Общая сумма входов и выходов дает возможность сравнивать структуры одного процесса и разные процессы по их сложности [3].

Таблица 1

Матрица связей функциональной  модели действий сложных систем  при централизованном способе управления

Table 1

Relationship matrix of functional model  of complex systems actions under  centralized control method

	Out1-2	А0	А1	А2	А3	А4	А5	А6	In1-2	Σin
Out1	0	0	1	0	0	0	0	0	0	1
Out2	0	0	0	0	0	1	0	0	0	1
А0	0	0	1	1	1	1	1	1	0	6
А1	0	1	0	1	1	0	0	0	0	3
А2	0	0	0	0	1	0	0	0	0	1
А3	0	0	0	0	0	1	0	0	0	1
А4	0	0	0	0	0	0	1	1	0	2
А5	0	0	0	0	0	0	0	1	0	1
А6	0	0	0	0	0	1	0	0	0	1
In1	0	0	0	0	1	0	0	0	0	1
In2	0	0	0	0	0	0	0	1	0	1
Σout	0	1	2	2	4	4	2	4	0	19

По матрице связей выполним расчет коэффициентов и эффективности процесса.

Масштабный коэффициент процесса.

Общее количество функций fΣ = 6, тогда

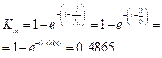
Коэффициент связанности функций процесса.

Общее число связей, то есть число единиц  в матрице SΣ=19, тогда

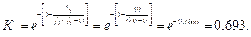
Коэффициент равномерности распределения функций в процессе.

Среднее число входных связей 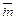 = 8; среднее число выходных связей 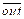= 12:

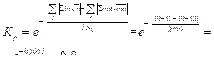
Коэффициент изолированности функций.

Число пустых строк пстр = 0, число пустых столбцов псто = 4, тогда

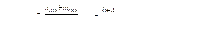
Эффективность процесса:

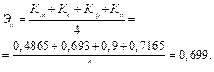
Процесс действий сложных систем при децентрализованном способе управления представлен на рисунке 2 в нотации технологии IDEF0. Он включает в себя шесть процедурных функций (А1…А6), выполняющих обработку информации, связанных между собой прямыми и обратными функциональными связями. Остальные действия выполняются так же, как и при централизованном способе управления.

Интерпретируя функциональную модель как орграф, сформируем матрицу связей функций моделируемого процесса (табл. 2).

Таблица 2

Матрица связей функциональной  модели действий сложных систем  при децентрализованном способе управления

Table 2

Relationship matrix of the complex  systems' functional model of actions under  decentralized control method

	Out1-2	А1	А2	А3	А4	А5	А6	In1-2	Σin
Out1	0	1	0	0	0	0	0	0	1
Out2	0	0	0	0	1	0	0	0	1
А1	0	0	1	1	0	0	0	0	2
А2	0	0	0	1	0	0	0	0	1
А3	0	0	0	0	1	0	0	0	1
А4	0	0	0	0	0	1	1	0	2
А5	0	0	0	0	0	0	1	0	1
А6	0	0	0	0	1	0	0	0	1
In1	0	0	0	1	0	0	0	0	1
In2	0	0	0	0	0	0	1	0	1
Σout	0	1	1	3	3	1	3	0	12

По матрице связей (табл. 2) выполним расчет коэффициентов и эффективности процесса.

Масштабный коэффициент процесса.

Общее количество функций fΣ = 6, тогда

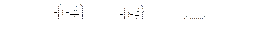
Коэффициент связанности функций процесса.

Общее число связей, то есть число единиц  в матрице SΣ=12, тогда

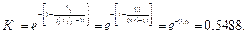
Коэффициент равномерности распределения функций в процессе.

Среднее число входных связей 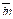 = 2; среднее число выходных связей 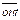= 6:

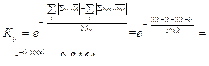
Коэффициент изолированности функций.

Число пустых строк пстр = 0, число пустых столбцов псто = 4, тогда

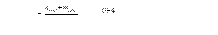
Эффективность процесса:

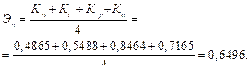
Процесс действий сложных систем при сетецентрическом способе управления представлен на рисунке 3 в нотации технологии IDEF0. Процесс включает в себя шесть процедурных функций (А1…А6), выполняющих, например, обработку информации, связанных между собой прямыми и обратными функциональными связями. Остальные действия выполняются так же, как и при централизованном способе управ- ления.

Интерпретируя функциональную модель как орграф, сформируем матрицу связей функций моделируемого процесса, представленную в таблице 3.

Таблица 3

Матрица связей функциональной  модели действий сложных систем  при сетецентрическом способе управления

Table 3

Relationship matrix of the complex  systems' functional model of actions under  the network-centric management method

	Out1-2	А1	А2	А3	А4	А5	А6	In1-2	Σin
Out1	0	1	0	0	0	0	0	0	1
Out2	0	0	0	0	1	0	0	0	1
А1	0	0	1	1	0	0	0	0	2
А2	0	1	0	1	0	0	0	0	2
А3	0	1	1	0	1	0	0	0	3
А4	0	1	0	0	0	1	1	0	3
А5	0	1	0	0	1	0	1	0	3
А6	0	1	0	0	1	1	0	0	3
In1	0	0	0	1	0	0	0	0	1
In2	0	0	0	0	0	0	1	0	1
Σout	0	6	2	3	4	2	3	0	20

По матрице связей (табл. 3) выполним расчет коэффициентов и эффективности процесса.

Масштабный коэффициент процесса.

Общее количество функций fΣ = 6, тогда

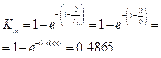
Коэффициент связанности функций процесса.

Общее число связей, то есть число единиц  в матрице SΣ=20, тогда

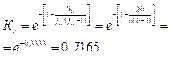
Коэффициент равномерности распределения функций в процессе.

Среднее число входных связей 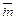 = 10; среднее число выходных связей  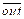= 14:

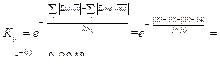
Коэффициент изолированности функций.

Число пустых строк пстр = 0, число пустых столбцов псто = 4, тогда

 

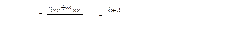
Эффективность процесса:

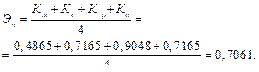
Расчет эффективности процессов функциональных моделей действий сложных систем в данном примере при различных способах управления при одинаковом числе функций позволяет сделать вывод, что наиболее эффективным является сетецентрический способ управления.

Заключение

В статье выполнен общий анализ функционального моделирования сложных систем при различных способах управления и выполнен расчет эффективности способов.

Предложенный метод позволяет количественно оценить эффективность систем и выбрать наиболее рациональную организацию процессов управления и функционирования сложных систем.

Также доказано, что возрастание числа процедурных функций функциональных моделей ведет к уменьшению эффективности процессов, а увеличение прямых и обратных функциональных связей функциональных моделей способствует ее увеличению.

Список литературы

1. Черемных С.В., Семенов И.О., Ручкин В.С. Моделирование и анализ систем. IDEF-технологии. М.: Финансы и статистика, 2006. 192 с.

2. Дубейковский В.И. Практика функционального моделирования с AllFusion Process Modeler. М.: Диалог-МИФИ, 2004. 464 с.

3. Ильин В.А., Янча С.П. Методы анализа функциональных моделей // Программные продукты и системы. 2009. Т. 22. № 4. С. 32–34.

4. Шпак В.Ф., Директоров Н.Ф., Мирошников В.И. и др. Информационные технологии в системе управления силами ВМФ. СПб: Элмор, 2005. 827 с.

5. Ильин В.А., Козлов И.Л. К проблеме автоматизации управления силами и средствами, функциональное
моделирование // Автоматизация процессов управления. 2009. № 4. С. 53–57.

6. Тебекин А. В. Методология функционального моделирования сложных технических систем модульного типа // Журнал технических исследований. 2021. Т. 7. № 2. С. 3–12.

7. Тебекин А.В., Тебекин П.А., Егорова А.А. Технологические трансформации XXI века как индуцирующий вектор перехода к новому качеству производства // Теоретическая экономика. 2021. № 1. С. 42–53.

8. Тебекин А.В., Петров В.С. Использование методологии моделирования IDEF при формировании структурно-параметрической модели реализации технологий обеспечения эффективного развития промышленных предприятий в условиях постиндустриальной экономики // Транспортное дело России. 2017. № 4. С. 43–49.

9. Харари Ф. Теория графов; [пер. с англ.]. М.: Книжный дом «Либроком», 2009. 296 с.

References

1. Cheremnykh, S.V., Semenov, I.O., Ruchkin, V.S. (2006) Modeling and Analysis of Systems. IDEF Technologies. Moscow, 191 p. (in Russ.).

2. Dubeykovskiy, V.I. (2004) Practice Functional Modeling with AllFusion Process Modeler. Moscow, 464 p. (in Russ.).

3. Ilin, V.A., Yancha, S.P. (2009) ‘Methods analisis of functional models’, Software & Systems, 22(4), pp. 32–34 (in Russ.).

4. Shpak, V.F., Direktorov, N.F., Miroshnikov, V.I. (2005) Information Technologies in the Navy Force Management System. St. Petersburg, 827 p. (in Russ.).

5. Ilyin V.A., Kozlov I.L. 2009. On the problem of automation of control of forces and means, functional modeling’, Automation of Control Processes, 4(18), pp. 53–57.

6. Tebekin, A.V. (2021) ‘Methodology for functional modeling of complex technical systems of modular type’, J.
of Tech. Research, 7(2), pp. 3–12 (in Russ.).

7. Tebekin, A.V., Tebekin, P.A., Egorova, A.A. (2021) ‘Technological transformations of the 21st century as
an inducing vector of transition to a new quality of production’, Theoretical Economics, (1), pp. 42–53 (in Russ.).

8. Tebekin, A.V., Petrov, V.S. (2017) ‘Using the modeling methodology IDEF in the formation of structural-parametric model for the implementation of technology ensure the efficient development of industrial enterprises in the condition of postindustrial economy’, Transport Business of Russia, (4), pp. 43–49 (in Russ.).

9. Harari, F. (1972) Graph Theory. Basic Books Publ., 274 p. (Russ. ed.: (2009) Moscow, 296 p.).